Atomen - Medica

Atomen
1. Elektromagnetisch spectrum
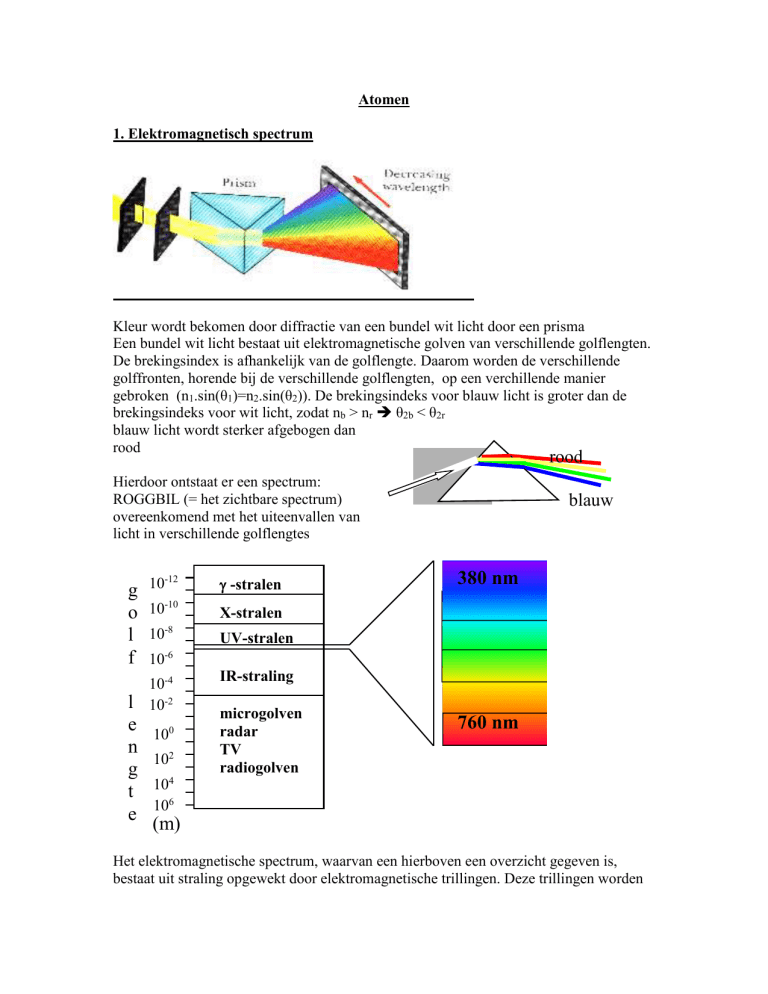
Kleur wordt bekomen door diffractie van een bundel wit licht door een prisma
Een bundel wit licht bestaat uit elektromagnetische golven van verschillende golflengten.
De brekingsindex is afhankelijk van de golflengte. Daarom worden de verschillende
golffronten, horende bij de verschillende golflengten, op een verchillende manier
gebroken (n1.sin(θ1)=n2.sin(θ2)). De brekingsindeks voor blauw licht is groter dan de
brekingsindeks voor wit licht, zodat nb > nr  θ2b < θ2r
blauw licht wordt sterker afgebogen dan
rood
rood
Hierdoor ontstaat er een spectrum:
ROGGBIL (= het zichtbare spectrum)
overeenkomend met het uiteenvallen van
licht in verschillende golflengtes
g
o
l
f
l
e
n
g
t
e
10-12
 -stralen
10-10
X-stralen
-8
10
blauw
380 nm
UV-stralen
-6
10
10-4
10-2
0
10
102
IR-straling
microgolven
radar
TV
radiogolven
760 nm
104
106
(m)
Het elektromagnetische spectrum, waarvan een hierboven een overzicht gegeven is,
bestaat uit straling opgewekt door elektromagnetische trillingen. Deze trillingen worden
opgewekt door elektrische wisselstroomkringen (radio), trillingen van moleculaire
dipolen tot trillingen van de magnetische momenten van atomen en kernen. Hetgeen
algemeen ‘licht’ (infrarood tot ultraviolet) genoemd wordt, vormt een deel van dit
spectrum. Het zichtbaar licht heeft golflengtes tussen λ=380 nm (blauw) en 760 nm
(rood).
ENERGIE:
Volgens de kwantumtheorie bestaat een elektromagnetische golf uit pakketjes, elk met
energie E = h.f. Hierin is f de frequentie van het licht en h de constante van Planck
h = 6,63 . 10 -34 J/s = 4,14 . 10-15 eV
f= c/λ met c=3,00 . 10 8m/s voor licht
E = hc/ = 1,24 . 10 -6 / λ eV (als de golflengte in m wordt uitgedrukt)
met λ=10-12 m voor γ stralen tot 10-1 m voor radiogolven. 1 eV = 1,602 . 10 -19 J. Dit is de
verandering van potentiële energie van een elementaire lading e als deze een
potentiaalverschil van 1 V doorloopt. Dit is ook gelijk aan de verandering van kinetische
energie van deze elementaire lading als deze zich zo verplaatst dat ze een potentiaalverschil van 1 V ondergaat.
Nota : in de beeldvorming geldt dat hoe kleiner de golflengte, hoe groter de resolutie?
Daarom geven X of γ stralen heel hoge resolutie maar ze hebben tegelijk ook heel veel
energie (zie biologische effecten van straling).
2. Relativiteit
Basis: Einsteins’ Postulaten
Relativiteitsprincipe: Alle wetten van de fysica zijn onafhankelijk van het inertiaalstelsel
(aan cte snelheid tov elkaar bewegende referentiestelsels).
Lichtsnelheid: Licht heeft steeds met de constante snelheid c in vacuum, ten opzichte van
eender welk inertiaalstelsel en onafhankelijk van de beweging van de lichtbron
(c= 3 . 108 m/s)
Implicaties
1) Relativiteit van gelijktijdigheid
2) Tijdsdilatatie(verlenging) en lengtecontractie
3) Relatieve massa en energie
De massa van een voorwerp is afhankelijk van de snelheid waarmee het zich
mo
1
voortbeweegt m =
met mo = rustmassa . We stellen γ =
v
v
1   ²
1   ²
c
c
Dan wordt de relativistische uitdrukking voor de energie: E = mc² = γ mo c²
Massa en energie zijn equivalent: massa kan omgezet worden in energie en energie kan
omgezet worden in massa, in materie. De wet van behoud van energie moet uitgebreid
worden tot wet wet van behoud van massa en energie. Als een 1ng (10-12 kg) massa
volledig getransformeerd wordt in energie, levert dit 90 kJ aan energie op.
De rustmassa van elementaire deeltjes kan uitgedrukt worden als energie :
me = (0,501 MeV) / c²
mp = (938,3 MeV) / c²
mn = (938,6 MeV) / c²
In het algemeen geldt (zie 1ste kand.): E² = p² c² + m0² c4
met p = bewegingshoeveelheid en m0 de rustmassa.
Maar LICHT heeft geen rustmassa dus: Elicht = p².c²
3. Quantumfysica
Geschiedenis
Stralingsspectrum (warmtestraling+...)
I = hoeveelheid energie uitgezonden per tijd in een bepaalde richting
Klassieke theorie : I = ρc ymax² ω² /2
 2c 
²
  
 .c. y max ²
I=
2
2 ² .c³ y max ²
I=
²
I= cte .
1
²
(hoe hoger T, hoe hoger ymax  hoe meer I
klassieke theorie
I
exper.

Experimenteel werd echter de onderbroken kromme in bovenstaande figuur opgemeten.
Planck slaagde erin dit gedrag theoretisch te verklaren door te stellen dat de energie
uitgezonden door een atoom (deze trilt met een bepaalde frequentie en hoe hoger de T
hoe intenser deze zal trillen) geen continue grootheid was, maar slechts welbepaalde
discrete waarden kan overnemen:
E=n.h.f
n=0,1,2,..
f=frequentie
h=cte van Planck = 6,6 . 10 -34 J.s
Atomen hebben discrete energietoestanden. Als de energie van een atoom verandert, zal
dit niet op een continue wijze gebeuren. Atomen zenden energie uit in energiepakketjes
met grootte nhf
Fotoelekrisch effect:
Opstelling : elektrische kring met een schakelelement dat bestaat uit een luchtledige
glazen bol waarin twee metalen plaatjes, een groot en een klein, op een zeker afstand van
elkaar geplaatst zijn. Over deze plaatjes wordt een potentiaalverschil aangebracht.
A) in een donkere kamer wordt er geen stroom gemeten
B) bij lichtinval op de grotere metalen plaat : kan, afhankelijk van de frequentie van het
invallend licht, een stroom gemeten worden.
Verklaring (Einstein 1905) : licht valt in op metalen plaat. Licht is samengesteld uit
deeltjes, fotonen, met energie hf. Deze lichtdeeltjes botsen met de vrije elektronen in het
metaal, en geven hun energie volledig af aan deze elektronen (volkomen niet elastische
botsing). Het elektron kan hiermee uit het metaal ontsnappen. Hiervoor heeft het een
energie W nodig. Uit het metaal gekomen heeft het elektron nog een kinetische energie
Ek.
hf = W + Ek . De kinetische energie Ek volstaat om de afstand tussen de twee plaatjes te
overbruggen en stroom te veroorzaken (ook al neemt de potentiële energie van de
elektronen toe (negatieve spanning).
Een elektromagentische golf (licht) heeft zowel golf- als deeltjesaspecten.
COMPTON effect
p, 0
e
p’, ’
pe
Voor licht is de energie E = pc. Hieruit lieden we uitdrukkingen af voor de hoeveelheid
beweging van een foton
 p (= mc) = E /c (want E = mc²)
 p = hf /c
 p = hf/ λf  p = h / λ
Als licht invalt op een metaal, of een materiaal met veel vrije elektronen, meet men een
verandering van de golflengte van het afgebogen licht. Dit kan niet verklaard worden met
de klassieke theorie van golven, maar wel als men licht als deeltjes (fotonen) beschouwd.
We nemen aan dat een foton een elastische botsing maakt met een elektron. De
elektronen van het materiaal nemen een deel van de energie van het invallend foton op.
Het foton zal daarom na de botsing een lagere energie hebben en bijgevolg een grotere
golflengte.
Interferentie bij elektronenbundels
heeft hetzelfde patroon als bij golven (deeltjes krijgen golfeigenschappen)
als a groot is - voldoende afstanden tussen maxima - onderscheiden = mogelijk
als a klein – overlappen – onderscheidensvermogen afh. van λ (hoe kleiner, hoe beter)
Kwantumtheorie : enkele consequenties van de vergelijking van Schödinger
E kan slechts discrete waarden aannemen
vb Waterstofatoom
U = -ke²/ r
met k=1/4πεo
En = Eo/n² = -13,6 eV/n²
Atoom structuur en spectra
En = -13,6 Zeff /n² eV
4 quantumgetallen
n
= hoofdquantumgetal
= maat voor de gemiddelde van een elektron tot de kern
= op welke schil
l
= orbitaal quantumgetal
= op welke orbita (s, p, d, ...)
= in welke (sferische) wolk
= 0, 1, ..., n-1
m
= magnetisch quantumgetal
= oriëntatie van de elektronenwolk
= vb: s: 1 oriëntatie, p : = 3 orientatie wolken
= l, l-1, ... , 0 , ... , -l+1,-l
s
= spinquantumgetal (+ ½, - ½ ). Dikwijls wordt een rotatie van het elektron om zijn als
als interpretatie voor spin gegeven, maar spin is een intrinsiek quantumgetal. Bij
magnetische interactie merken we pas dat deeltjes een spin hebben.
 E wordt bepaald door n (gelijk aan de gemiddelde afstand tot de kern)
Maar voor 1 n zijn er verschillende golffuncties mogelijk: men zegt dat de energieniveaus
gedegenereeerd zijn
 deze verschillende mogelijkheden voor ψ worden geparametiseerd door de
nevenquantumgetallen m en l en op deze plaats (gegeven door ψ) komen 2 elektronen
voor waartussen nog onderscheid gemaakt wordt door s
BOSONEN:
enkel gehele getallen als mogelijke spinwaarden: -2,-1,0,1
er kunnen er ∞ veel in dezelfde kwantumtoestand zitten
vb: fotonen
FERMIONEN enkel halve getallen als mogelijke spinvoorwaarde:- ½ , ⅔ ,....
maar 1 fermion per quantumtoestand
elektron, proton
Notatie: toestand van een elektron rond de kern
E1 : (1, 0, 0, ½ )
de 1 staat voor 1e schil, de vier getallen staan voor quantumwaarden van (n,l,m,s)
Energieniveaus
De orbitalen waarin de elektronen zich kunnen bevinden hebben elk hun eigen
energieniveau. E1 (voor de 1e schil) is de grondtoestand en dus het laagste energieniveau
(en dit is negatief omwille van de negatieve potentiële energie die overweegt op de
positieve kinetische energie)
E2, .... hebben steeds een hogere E (meer naar 0) door stijgende n in de vergelijking
Ongebonden elektronen: voor energiewaarden groter dan E=0 (n=∞) komt een elektron
in een continu energiespectrum terecht. Veranderingen van energie zijn dan continu.
De overgangswaarschijnlijkheid van een enrgieniveau naar een ander wordt bepaald door
behoudswetten (energie, impulsmoment, spin...). daardoor zijn niet alle overgangen
mogelijk.
Excitatie, de-excitatie en ionisatie
excitatie = elektronen van een lage naar een hogere energie toestand brengen
 er moet voldoende E toegevoegd worden
vb.: om een elektron vrij te krijgen (ionisatie): E toevoegen = Eo/n²
-Eo/n² + Eo/n² = 0
E=0  deeltje is vrij. De totale energie is gelijk aan nul en dit betekent dat de potentiële
energie nul kan worden (als de kinetische energie ook nul is), en dat wil zeggen dat het
elektron oneindig ver van de kern kan zijn. Excitatie kan
 Door temperatuur te verhogen : Moleculen trillen harder  elektronen botsen 
Energie oppikken van een ander deeltje  naar hogere E niveau En  En+k
 Door licht (=elektromagnetische energie) te laten invallen: fotonen met E =hf, E
is het energieverschil tussen de twee orbitalen.
 Door de atomen in een (sterk) elektrisch veld te plaatsen (verhogen van de
elektrostatische potentiële energie)
Behoud van energie, wet van ‘arbeid’ en energie:
En+k – Ek = hf
(voor de juiste energie moet je dus f ~ 1/λ aanpassen)
Overgangswaarschijnlijkheid mag niet 0 zijn: als de hoger gelegen schil volzet is, vb op
n=2 zitten reeds 8 elektronen dan kan er daar geen meer bij moet je meteen nog hoger
wat meer E vereist
De-excitatie : van een hoger naar een lager E–niveau gaan
 E wordt vrijgegeven onder de vorm van elektromagnetische straling met bepaalde λ:
E = hf en f = c/λ
Absorptiespectrum : men stuurt licht door een bepaald atomair gas dat daarna invalt op
een Newton prisma. Het prisma splitst het doorgelaten licht op in monochromatische
lichtstralen door een verschillend brekingshoek) voor de verschillende kleuren
(verschillende λ hebben een verschillend brekingsindex). We vangen het lichtspectrum op
op een scherm, maar er zullen bepaalde golflengten ontbreken. Dit is waar te nemen als
zwarte strepen in het bandenspectrum. De kleuren die niet aanwezig zijn, zijn
geabsorbeerd door het gas omdat met die golflengte de fotonen de juiste energie hebben
om de elektronen in excitatie te brengen. De ligging van deze strepen is typisch voor een
bepaald atoom. We kunnen daarom het spectrum gebruiken voor het identificeren van
atomen.
Emissiespectrum : Bij verwarming van een gas zullen de elektronen in een geëxciteerde
toestand geraken en bij het terugvallen naar hun oorspronkelijke toestand licht van
bepaalde golflengte uitzenden. Welke en hoeveel emissielijnen zichtbaar zijn hangt af
van het soort atoom en de toegeveoegde energie.
vb.: E1 en E2 aanwezig : als er alleen elektronen van E2 naar E1 terugvallen dan bekomt
men maar één emissielijn met hf= E2 - E1
vb : E1 , E2 en E3 aanwezig. Drie emissielijnen mogelijk met elk hun verschillend waarde
voor E (E2  E1 ; E3  E2 ; E3  E1)
4. Lasers
Gestimuleerde emissie
(basisprincipe van lasers)
Als een elektron in een atoom in een geëxciteerde toestand (Em) is, het atoom interageert
met een invallend foton met f waarvoor hf = Em – E0 (E0 is de energie van de
grondtoestand), dan kan dit elektron terugvallen naar zijn grondtoestand. Het atoom zend
dan een foton uit met dezelfde f en coherent met het invallend foton. Het foton ‘spoort’
het geëxciteerde elektron aan om naar een lagere energietoestand te gaan.
LASER = Light Amplification by Stimulated Emission of Radiation
Coherent betekent : de golven zijn in fase en gaan in dezelfde richting. Door het feit dat
de golven in fase zijn is er positieve interferentie, met een versterking van de resulterende
amplitude A (toename intensiteit)
Het cumultatief effect: als fotonen met gepaste frequentie nterageren met veel
geëxciteerde atomen, ontstaat een sterke monochromatische stralenbundel.
Excitatie
Hoe breng je de atomen in de vereiste geëxciteerde toestand ? We illustreren dit met een
3-niveau laser (3 energieniveaus spelen een rol : de grondtoestand E0, een geëxciteerde
toestand En en een metastabiele toestand Em, waarvan de energie net iets lager is dan En,
zie figuur hierboven) . Door een energiestoot wordt het actief medium (materie die zorgt
voor het laserlicht) naar een hogere energietoestand gebracht, (een waarvoor de
overgangswaarschijnlijkheid zeer groot is; omdat de overgang van een laag energieniveau
naar een hoger metastabiel niveau onwaarschijnlijk is). Vanuit deze toestand kunnen de
elektronen terugvallen naar het lager metastabiel niveau (dit gebeurt in enkele ns). De
elektronen blijven lang ( microseconden tot minuten) in deze metastabiele toestand.
De overgang naar de hogere energietoestand kan gerealiseerd worden door een lichtflits
of door een heel hoge spanning aan te brengen. Door het aanbrengen van een groot
potentiaalveld zullen de elektronen van hun kern worden weggetrokken en gemiddeld
verder van de kern bewegen, dus een hogere energie hebben.
Daarna volgt de overgang van En naar de metastabiele toestand Em, komt een energie
En – Em vrij. Deze energie wordt niet gebruikt in de laser, maar wordt warmte die moet
afgevoerd worden. Het rendement is dus omzeggens nooit 100% .
Omdat de elektronen gemiddeld genomen heel lang in deze metastabiele toestand blijven,
kan er op dit moment gestimuleerde emissie gerealiseerd worden. Door een zeer groot
aantal elektronen in de aangeslagen metastabiele toestand te brengen realiseert men een
populatie-inversie.
Resultaat
Een sterke coherentie  grote amplitude: hoge energie op atomaire schaal
(positieve interferentie)
- Een sterk gerichte straal: door negatieve interferentie in de andere richtingen
- Monochromatisch: 1 frequentie met hf= Em– E0
Wat nodig?
- atomen in aangeslagen metastabiele toestand  POMP
- veel goede invallende fotonen  SPIEGELS
-
Praktisch
Excitatie van de actieve substantie( = lasing materiaal)  pomp
- belichten met flitslamp met hoogfrequente emstraling
(hfp = ∆ E + hf)
- elektromagnetisch veld (hoge potentiaal)
Op een bepaald ogenblik is het merendeel van de atomen geëxciteerd door de spontane
terugval van de elektronen naar de metastabiele toestand (=populatie-inversie: meer
elektronen in geëxciteerde toestand dan in de lage energie-toestand)
Gestimuleerde emissie:
Als een elektron spontaan naar de grondtoestand terugvalt, zendt deze een foton uit dat
dan langs de andere geëxciteerde atomen komt en daardoor nieuwe fotonen zal doen
ontstaan
Door de weerkaatsing tegen de spiegels, blijven ze in het actief medium, waarna ze meer
en meer atomen bereiken en de straal versterken.
Rechts is er een halfdoorlatende spiegel waardoor de stralen langs hier naar buiten
kunnen indien er genoeg zijn
Rechts ontsnapt er monochromatisch licht met een golflengte variërend van 10-6m (IR)
tot 10-7m (UV)
Types
Medium:
-
-
CO2: gebruikt voor warmte: iets toelassen dmv warmte: zeer gericht = voordeel
van een laser
YAG: H2O verdampen = substantia afbreken
o tanden bleken: H2O weg  poeder blijft over
o gaatjes boren
o tandplak verwijderen
o wijnvlekken uit de huid verwijderen
Dye: kleurlaser, emulsie vormen met één of andere vloeistof
Robijn: overzenden van signalen aangezien er weinig energieverlies is
Vb. aarde  maan
Excimen: oftalmologie: krasjes in hoornvlies om zicht te verbeteren
Argon: chirurgisch snijden in het operatiekwartier
Werking:
1) continu: maximal enkele mWatt vermogen
2) gepulseerd: puls van 1µs en elke ms herhalen. Per puls mag het vermogen 1000x
groter zijn, want het gemiddelde vermogen (=Pg) zal toch laag genoeg zijn en je kan zo
dus een hogere ΔE (= P . Δt) bereiken
GEBRUIK
Radiotherapie=behandeling van tumoren
Men brengt een bepaald medicijn: optisch actieve moleculen, tot bij de tumor via
bloedbaan. Door de laser breng je deze moleculen in excitatie waardoor deze in werking
schieten en de tumor afgebroken wordt
Holografie=techniek om 3D beelden vast te leggen en te visualiseren met behulp van een
laser op een vlak oppervlak. Een laserstraal wordt gericht op een halfdoorlatende spiegel
A) een deel gaat door de spiegel
B) een deel weerkaatst en botst tegen het 3D object, waar het dan terug weerkaatst wordt
 er zal een interferentie ontstaan, dit interferentiepatroon wordt zichtbaar op de
fotografische plaat: deze wordt ontwikkeld
 daarna wordt deze plaat belicht door dezelfde laser of wit licht in dezelfde richting en
verschijnt het 3Dbeeld
Laser wordt hier enkel gebruikt als monochromatisch lichtbron, om een
interferentiepatroon te genereren.
5. X-Stralen
Eigenschappen.
1) Energie
E  h. f 
h.c


1,24.10 6 (eV )
 (m)
laser: zwak 10-6 m  1,24 eV
sterk 10-7 m  12,4 eV
X-Stralen: hoogfrequente elektromagnetische straling !
10-8 m  124 eV
10-10 m  12400 eV
ontdekt in 1895 door Wilhelm Röntgen
(nota bene: zeer toevallig: sloot zijn labo af en zag ’s anderendaags toch een fotoplaat die
op zijn bureau lag met afbeeldingen van de kristallen die eronder lagen)
2) Doordringbaarheid: X-stralen worden niet sterk geabsorbeerd. Ze zijn daardoor wel
zeer doordringend: absorptie voor lucht=nihil; water=zwak, botten(Ca2+) = zeer sterk,
waardoor deze zichtbaar kunnen gemaakt worden.
Bremsstrahlung: elektromagnetische straling die ontstaat door het afbuigen van geladen
deeltjes (hier elektronen). Komt voor in deeltjesversnellers.
X-stralenbuis
De kathode maakt elektronen aan: thermische elektronen. Deze worden versneld door
potentiaalverschil (ca. 80 keV) en dan gestuurd naar de anode, waar ze vertraagd worden
door de elektrische krachten van de andere atomen die erop inwerken (botsingen met de
ionen van de anode). Deze elektronen verliezen kinetische energie en dit zenden ze uit
onder de vorm van fotonen
Men verkrijgt een straling met een continu spectrum:
Sommige geven 1 foton af met E=Ek, anderen geven er meerdere af waardoor er
verschillende golflengtes vrijgegeven worden. De enige regel is: de E van alle fotonen
geproduceerd door 1 elektron is gelijk aan de oorspronkelijke kinetische energie van dat
elektron.
Verschillende golflengtes komen vrij: door de grote hoeveelheid elektronen is het
spectrum van de vrijkomende golflengtes continu. Er is een minimale golflengte, omdat
als bij de maximale kinetische energie alle energie omgezet wordt in een foton de
frequentie hiervan gelijk is aan e.ΔV/h. Dit is de hoogste frequentie die we kunnen halen,
en komt overeen met de laagst mogelijke golflengte. Dit is de wet van Duane-Hunt.
h.c
h.c


E
e.V
Duane-Hunt: de begingolflengte daalt naarmate de aangelegde spanning stijgt
Karakteristieke straling
Hier wordt ook zo’n versneld thermische elektron op de anode afgestuurd, maar deze zal
botsen met een atoom in plaats van gewoon te vertragen
De elektron botst, geeft genoeg energie aan een K-schil – elektron om te ontsnappen en
vliegt dan verder aangezien het zelf nog genoeg energie (= ca. 80 keV tegenvover 40 eV
bindingsenergie van een K-schil – elektron) overheeft.
De K-schil mist een elektron Hierdoor zal een M- of L–schil – elektron naar deze K-schil
verplaatsen en tegelijk een h.f foton uitzenden.
In het spectrum van X-stralen dat uitgezonden wordt, komen deze bepaalde golflengten
veel sterker naar voor dan de continue verdeling van de golflengte door Brehmsstrahlung
Röntgenbuis
= opstelling met anode en kathode in een loden omhulsel
X-stralen veel schadelijker zijn dan lasers (daarom een loden omhulsel, dit houdt Xstralen tegen)


ioniserend: als ze botsen met atomen, zullen ze de elektronen ervan weghalen
enorm doordringend:
o omdat het zo’n hoge energie heeft dat het veel botsingen met atomen kan
ondergaan voor het uitsterft hoe hoger de energie = hoe doordringender
o radio, ... praktisch overal doorheen behalve sommige metalen
o X-stralen worden sterk door Ca2+ geabsorbeerd
BEELDEN
X-stralenbron stuurt de stralen op een voorwerp, de stralen worden gedeeltelijk
geabsorbeerd en gaan gedeeltelijk door het voorwerp. De stralen die door het voorwerp
gaan, worden op een scherm opgevangen. Dit kan een fotogevoelig scherm waarop Xstralen een fotografische werking heeft of lichtgevoelige materiaal dat de invallende
intensiteit omzet in een spanningspuls (beeld op TV-scherm). We bekomen dus een
schaduwbeeld.
 sterke absorptie: blijft wit
 zwakke absorptie: wordt donker
(nota bene: Barium houdt ook tegen; vandaar dat men bariumpap toedient om het
spijsverteringskanaal te onderzoeken)
CT (computertomografie) CAT (computer assisted tomografie)
 “doorsneden” maken met behulp van X-stralen
 Een 3Dbeeld verkijgen door de opeenvolgende doorsneden via een computer te laten
verwerken
Roterende X-stralenbron:
deze zal vanuit een bepaalde positie stralen sturen naar de detectoren die in de hele ronde
zijn geplaatst (= halfgeleiders waarbij de fotonen een spanning opwekken die gemeten
wordt)
Als de meting gedaan is, draait de bron 1° en zoverder tot een hele omwenteling gedaan
is.
De lichte vlakken zijn het resultaat van de absorptie van die stralen.
De computer krijgt alleen de informatie van de projecties op het scherm maar door terug
te rekenen (vandaar computer) en de twee te combineren, kan men bepalen waar er een
voorwerp aanwezig was (zie figuur). Door een roterende bron hebben niet twee
projecties om terug te rekenen, maar een groter aantal.