Toets elektriciteit 15 november 2000

Oplossingen toets elektriciteit
6 november 2002
groep: 1B
Vraag 1:
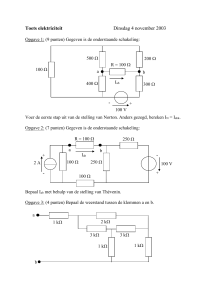
Gegeven is de schakeling
5 k
a
1 k
1 k
b
+
+
10 V
Iab = ?
5 k
-
1 mA
10 k
-
Bereken de stroom Iab met behulp van de stelling van Thévenin. Bereken ook het
vermogen welke gedissipeerd wordt in die weerstand van 1 k.
Oplossing:
Een stroom Iab uitrekenen met behulp van de stelling van Thévenin behelst drie
stappen.
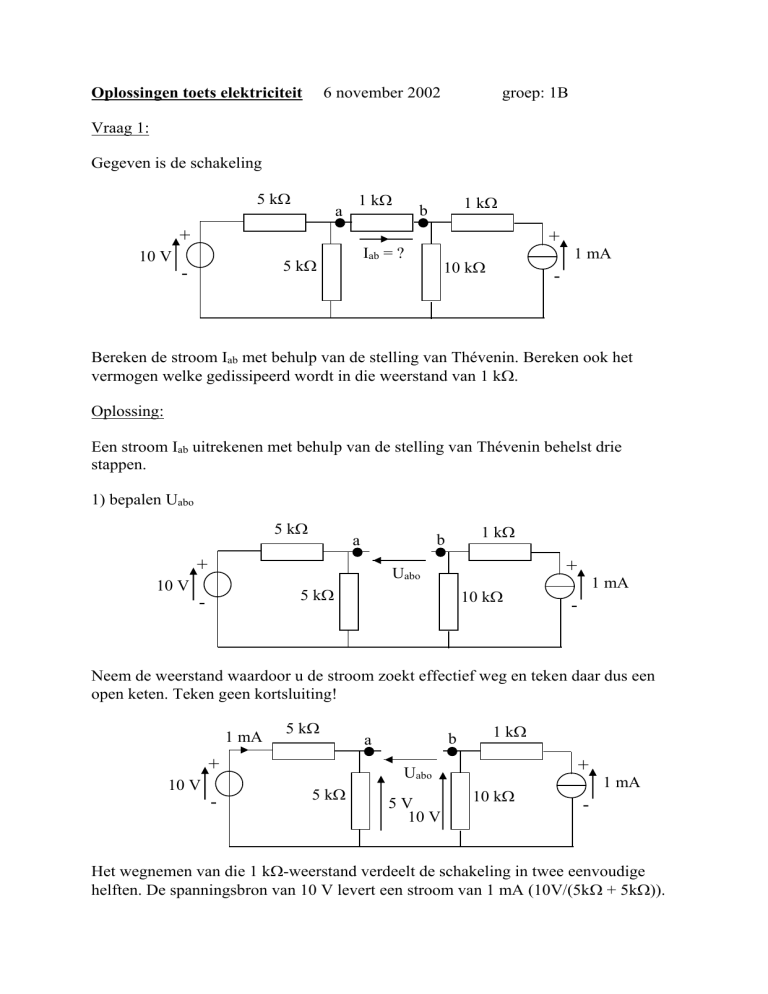
1) bepalen Uabo
5 k
1 k
b
a
+
+
Uabo
10 V
1 mA
5 k
-
10 k
-
Neem de weerstand waardoor u de stroom zoekt effectief weg en teken daar dus een
open keten. Teken geen kortsluiting!
1 mA
5 k
+
10 V
-
b
a
1 k
+
Uabo
5 k
5V
10 V
1 mA
10 k
-
Het wegnemen van die 1 k-weerstand verdeelt de schakeling in twee eenvoudige
helften. De spanningsbron van 10 V levert een stroom van 1 mA (10V/(5k + 5k)).
Hierdoor staat over de weerstand van 5 k een spanning van 5 V. Let hierbij op de
polariteit.
De stroombron rechts levert een stroom van 1 mA zodat over de 10k-weerstand een
spanning van 10 V staat. Let hierbij steeds goed op met de polariteiten!!
Nu kunnen we de spanningswet van Kirchoff toepassen die zegt dat in ons voorbeeld
10 V + Uabo – 5 V = 0.
Dit betekent dat Uabo = - 5 V. (let op het teken)
2) bepalen RV vanuit de klemmen a en b
Bij het bepalen van RV kijkt u vanuit de klemmen a en b (niet vanuit een ander
gezichtspunt zoals een spanningsbron of stroombron). U stelt ook alle bronnen nul, dit
betekent:
Spanningsbron nul stellen == kortsluiten
Stroombron nul stellen == open keten maken
Ook neemt u hier de 1k-weerstand tussen a en b weg!!!
We krijgen zo de onderstaande schakeling:
RV
5 k
b
a
5 k
1 k
10 k
Dit betekent dat RV = 10k + (5k // 5k) = 12,5k.
3) Nu het eigenlijke uitrekenen van Iab = Uabo/(RV + R) = -0,37 mA. Want hier zoeken
we de stroom Iab door de weerstand R = 1k.
RV = 12,5 k
a
Iab
R = 1k
Uabo = -5V
b
Teken ook het Thévenin-equivalent schema.
Hier is ook gevraagd wat het gedissipeerd vermogen is in de weerstand R = 1k.
Welnu,
P = R Iab = UabIab = 0,137 mW.
Het is echter zo dat Uab  Uabo zodat P  UaboIab.
Let op:
Als u spanningen van de grootte-orde volt hebt en weerstanden van de grootte orde
k, dan krijgt u stromen van de grootte-orde mA. De gedissipeerde vermogens zijn
dan ook van de grootte-orde mW.
Vraag 2:
Gegeven is de schakeling
1000 
+
1A
300 
1000 
100 
a
200 
b
R = 200 
300 
Voer de tweede stap uit van de stellingen van Thévenin en Norton. Anders gezegd,
bereken de vervangingsweerstand RV gezien vanuit de klemmen a en b.
Oplossing:
Het is nuttig eerst het schema te hertekenen, maar met alle bronnen nul gesteld wat
betekent
Spanningsbron nul stellen == kortsluiten
Stroombron nul stellen == open keten maken
Verder ook de weerstand R tussen a en b wegnemen en nu RV bepalen bekeken vanuit
de klemmen a en b (niet vanuit het standpunt van bijvoorbeeld de nulgemaakte bron).
1000 
300 
1000 
100 
a
200 
b
300 
RV
Die linkse 1000  hangt los te slingeren en heeft geen enkel effect.
Teneinde RV te bepalen is een driehoek-ster-transformatie nodig. Zo wordt een
driehoek gevormd door de weerstanden 1000 , 300  en 200 . Door deze driehoek
om te rekenen naar een ster bekomen we de onderstaande figuur.
200 
100 
40 
a
b
RV
300 
133 
Let wel op dat de weerstanden van de ster op de goede plaats geplaatst worden!
Nu hebben we een gemengde serie-parallel-schakeling bekomen. We bekomen dan
ook dat
RV = 40 + (300 // 433) = 217.
Vraag 3:
Bepaal de stroom Iab in de onderstaande schakeling met behulp van het superpositieprincipe. (gebruik de stellingen van Norton of Thévenin niet!)
1
2
1A
1
2A
a 3
10 
Iab
1
b
Oplossing:
Bij de superpositiemethode worden twee netwerken afgeleid. Het eerste netwerk heeft
enkel de stroombron van 2A en het tweede netwerk heeft enkel de stroombron van 1A.
Een stroombron nul maken, betekent dat je deze vervangt door een open keten.
1) Het eerste netwerk wordt dan ook:
1
2
1
2A
a 3
10 
Iab,1
1
b
Dit tweede netwerk kan vereenvoudigd worden tot:
2
2A
4
a
1
10 
Iab,1
b
zodat
2A
a
1
11,33 
Iab,1
b
We bekomen dan ook dat Iab,1 = 2A .(1/(1 + 11,33)) = 0,162 A.
2) Het tweede netwerk wordt dan ook:
1
2
1
a 3
1A
10 
Iab,2
1
b
Herken de driehoek bestaande uit 1, 2 en 3. Via een driehoek-ster-transformatie
kan die driehoek vervangen worden door een ster met weerstandswaarden 0,33, 1
en 0,5.
0,33 
0,5 
1
a
1
1A
10 
Iab,2
1
b
Hieruit weten we dat Iab,2 = 1A (1,33/(1,33 + 11)) = 0,108 A.
3) Volgende uit het superpositieprincipe weten we dat Iab = Iab,1 + Iab,2 = 0,27 A.
Let op:
Kies de zin van Iab, Iab,1 en Iab,2 aan elkaar gelijk.
Algemene opmerkingen:
Pas steeds de gevraagde methode toe.
Maak duidelijke figuren.