Slinger - WisNet

Slinger
©Wisnet-hbo april 2009
Analytische bepaling van uitwijking, snelheid en versnelling van een voorwerp met massa m
dat aan een touw hangt.
1 Beschrijving van de situatie
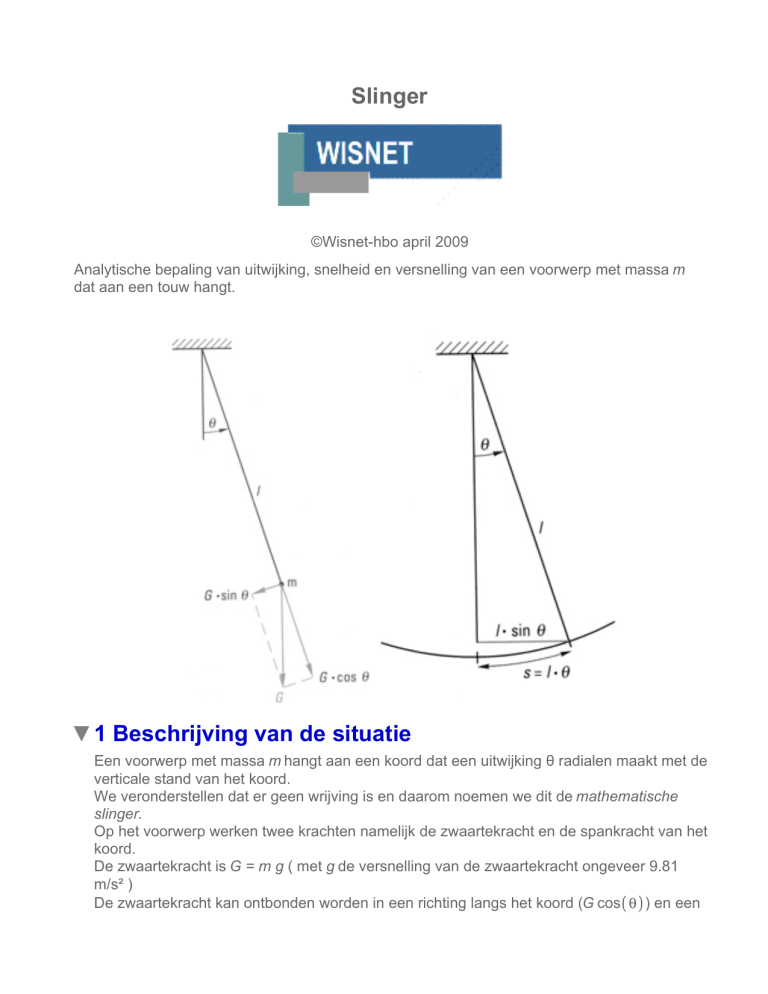
Een voorwerp met massa m hangt aan een koord dat een uitwijking θ radialen maakt met de
verticale stand van het koord.
We veronderstellen dat er geen wrijving is en daarom noemen we dit de mathematische
slinger.
Op het voorwerp werken twee krachten namelijk de zwaartekracht en de spankracht van het
koord.
De zwaartekracht is G = m g ( met g de versnelling van de zwaartekracht ongeveer 9.81
m/s² )
De zwaartekracht kan ontbonden worden in een richting langs het koord (G cos
) en een
richting loodrecht daarop (G sin(θ)).
De component langs het koord wordt opgeheven door de spankracht in het koord.
Blijft over de kracht G sin
die voor de beweging zorgt en is dus in feite de enige kracht
die overblijft en steeds tegengesteld aan de uitwijking s = l .
Deze uitwijking s (langs de cirkel boog) is een functie van t en kan dus geschreven worden
als
s t =l
t
De snelheid v is dan:
d t
v t = ds t =l
dt
dt
De versnelling a is dan:
2
d s t
a t =
2
=l
d
2
t
2
dt
dt
De krachtenvergelijking kan nu opgeschreven worden:
Ftot = G sin
Omdat de totale kracht altijd zorgt voor een uiteindelijke versnelling volgens de wet van
Newton:
Ftot = m a
Krijgen we de differentiaalvergelijking van de slinger:
d
ml
2
t
2
= m g sin
t
dt
Ook wel anders geschreven met de massa m uit de formule weggedeeld en herleid op 0.
l
d
2
t
2
g sin
t
=0
dt
Vervolgens passen we de benadering toe die geldig is voor kleine waarden van θ, immers
de hoek (in radialen) moet niet al te groot genomen worden bij de mathematische slinger
(want dan wordt de beweging veel groter en dus ook meer wrijving).
sin
De differentiaalvergelijking van de mathematische slinger:
2
d
t
2
dt
g
l
t =0
Opvallend is dat de massa van het voorwerp niet meer in de formule staat.
In het algemeen neemt men voor de massa van het voorwerp een niet al te kleine massa
om de invloed van de luchtwrijving relatief niet al te groot te laten zijn.
2 Oplossing van de differentiaalvergelijking
De differentiaalvergelijking van de mathematische slinger.
2
d
t
g
l
2
dt
t =0
Stel de algemene oplossing van de differentiaalvergelijking.
t = A cos
t
B sin
t
Bepaal de eerste afgeleide én de tweede afgeleide van θ(t)
d
d
t
dt
2
t
2
= A
= A
sin
2
cos
t
B
t
cos
B
2
sin
t
t
dt
Deze oplossing invullen in de differentiaalvergelijking van de mathematische slinger:
A
2
cos
t
B
2
sin
g
A cos
l
t
t
g
B sin
l
t =0
Dit klopt precies als je voor ω het volgende invult:
=
g
l
De constanten A en B zijn willekeurige constanten die afhangen van de beginsituatie op
tijdstip t = 0.
Randvoorwaarden 1
Stel de oplossing van de differentiaalvergelijking:
t = A cos
t
B sin
t
Als je aanneemt dat op t = 0 het voorwerp zich in de uiterste stand bevindt met uitwijking
, dan is A gelijk aan
.
max
max
(Immers de cosinus is op t = 0 gelijk aan 1).
Verder moet er nóg een gegeven zijn (omdat het een tweede orde
differentiaalvergelijking is) .
Je kunt nagaan dat het voorwerp geen snelheid heeft op het moment van het bereiken
van de uiterste stand.
Op tijdstip t = 0 is dan de snelheid gelijk aan 0.
d
t
dt
= A
sin 0
B
cos 0 = 0
Je kunt dus nagaan dat dan B = 0.
De oplossing van de differentiaalvergelijking voor de uitwijkingshoek θ in radialen is dan
met deze randvoorwaarden:
t =
cos
max
g
t
l
met randvoorwaarden dat het voorwerp op t = 0 in de uiterste
stand
max
in rust is.
Randvoorwaarden 2
Stel de oplossing van de differentiaalvergelijking:
t = A cos
t
B sin
t
Als je aanneemt dat op t = 0 de slinger zich in de evenwichtsstand bevindt, dan is A
gelijk aan 0.
(Immers de cosinus is op t = 0 gelijk aan 1).
Verder moet er nóg een gegeven zijn (omdat het een tweede orde
differentiaalvergelijking is) .
Je kunt nagaan dat het voorwerp een maximale snelheid heeft op het moment van het
bereiken van de uiterste stand.
Op tijdstip t = 0 is dan de snelheid gelijk aan.
d
t
dt
= A
Je kunt dus nagaan dat dan B =
De maximale snelheid is dan dus
sin 0
B
cos 0 = 0
.
max
max
.
De oplossing van de differentiaalvergelijking voor de uitwijkingshoek in radialen is dan
met deze randvoorwaarden:
t =
sin
max
g
t
l
met randvoorwaarden dat het voorwerp zich op t = 0 in de
evenwichtsstand bevindt met maximale snelheid.3
3 Frequentie, hoekfrequentie en slingertijd
In het bovenstaande is de hoeksnelheid is of ook wel de hoekfrequentie genoemd.
Het betekent dat éen slingering voltooid wordt in één periode van de beschreven sinus.
Als f de frequentie is (aantal volledige slingeringen of omwentelingen per seconde) dan is ω
= 2 π f het aantal radialen per seconde.
De slingertijd T is de tijd die het kost om één slingering of omwenteling te voltooien.
De hoekfrequentie bij slingeringen of draaiingen is dus altijd:
=2 f
De slingertijd T is altijd:
T=
2
1
=
f
In het geval van de mathematische slinger is de slingertijd T :
T=2
l
g
Aan deze formule is te zien dat de slingertijd T helemaal niet afhangt van de massa van het
voorwerp.
Verder wordt de slingertijd T groter naarmate de slingerlengte l groter wordt.
De slingertijd T wordt groter naarmate de versnelling van de zwaartekracht g juist kleiner
wordt.
Dus op de maan bijvoorbeeld zal de slinger langzamer bewegen. Immers de zwaartekracht
is daar veel minder.