[Trek de aandacht van uw lezer met een veelzeggend citaat uit het

Oefenmateriaal werkcollege 1 Gravitatie in het heelal
Deze opgaven en samenvattingen zijn ook terug te vinden in H17 Pulsar VWO. Het is
handig om Binas te raadplegen voor extra gegevens. Veel plezier met de opgaven
Exoplaneten zijn planeten bij andere
sterren. Een manier om een exoplaneet te
ontdekken is de transitmethode.
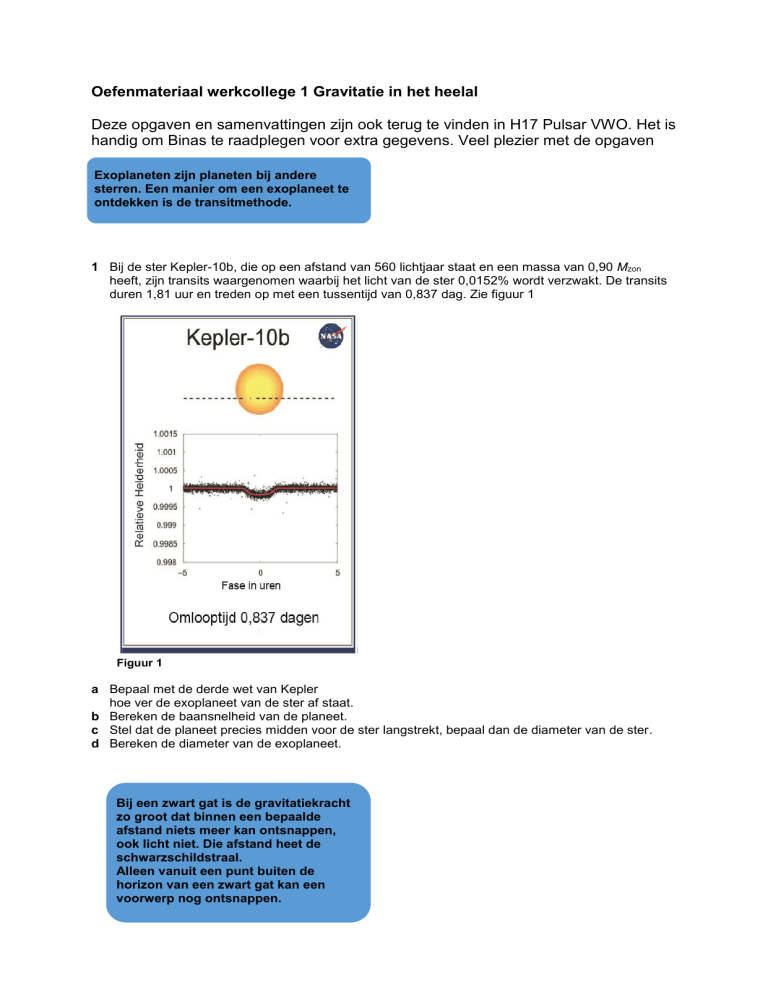
1 Bij de ster Kepler-10b, die op een afstand van 560 lichtjaar staat en een massa van 0,90 Mzon
heeft, zijn transits waargenomen waarbij het licht van de ster 0,0152% wordt verzwakt. De transits
duren 1,81 uur en treden op met een tussentijd van 0,837 dag. Zie figuur 1
Figuur 1
a Bepaal met de derde wet van Kepler
hoe ver de exoplaneet van de ster af staat.
b Bereken de baansnelheid van de planeet.
c Stel dat de planeet precies midden voor de ster langstrekt, bepaal dan de diameter van de ster.
d Bereken de diameter van de exoplaneet.
Bij een zwart gat is de gravitatiekracht
zo groot dat binnen een bepaalde
afstand niets meer kan ontsnappen,
ook licht niet. Die afstand heet de
schwarzschildstraal.
Alleen vanuit een punt buiten de
horizon van een zwart gat kan een
voorwerp nog ontsnappen.
[Trek de aandacht van uw lezer met een
veelzeggend citaat uit het document of
gebruik deze ruimte om een belangrijk
punt te benadrukken. Sleep dit tekstvak
als u het ergens anders op de pagina
wilt plaatsen.]
2 a Bereken de straal van de horizon voor een zwart gat met de massa van de aarde.
b Bereken hoe groot de dichtheid van de aarde wordt (in kg/dm3) als zij tot een balletje ter
grootte van haar horizonstraal wordt samengeperst.
c
Beantwoord dezelfde vraag voor de zon.
3 a
b
c
d
Als de straal van een bol gelijk is aan zijn schwarzschildstraal geldt deze formule:
𝑐
𝑅=
√8/3π𝐺𝜌
Hierbij is ρ de dichtheid van de bol.
Leid deze formule af.
Bereken hoe groot de massa van een bol materie met de dichtheid van water moet zijn, om
ervoor te zorgen dat zijn straal gelijk is aan zijn horizonstraal.
Reken de massa van b om naar zonmassa’s.
Beantwoord dezelfde vraag voor een bol met de dichtheid van lucht.
4 Bereken de horizonstraal Rh van het zwarte gat in het Melkwegcentrum als je weet dat het een
massa heeft van 4,5 zonsmassa’s
.
Licht kan door het zwaartekrachtsveld
van een zwaar object worden
afgebogen. Dit heet
gravitatielenswerking
5 Je ziet een cirkelvormige Einsteinring. De hoek, gemeten vanaf de aarde, tussen het centrum en de
rand van de ring is θ.
Je meet dat θ = 3,4·10-4 graden. De Einsteinring ontstaat doordat het licht van een quasar (de
heldere kern van een ver sterrenstelsel) op een afstand van 10 miljard lichtjaar wordt afgebogen
door een object op een afstand van 1,5 miljard lichtjaar.
De massa van het als lens fungerende stelsel kun je berekenen met deze formule:
𝑀lens =
5 ∙ 1020 ∙ 𝜃 2 ∙ 𝑑quasar ∙ 𝑑lens
(𝑑quasar − 𝑑lens )
De afstanden d in deze formule zijn in miljard lichtjaar en de massa van de lens is in de eenheid
zonsmassa.
a Leg aan de hand van een tekening het principe van de gravitatielens uit. Geef in de tekening
de afstanden dquasar en dlens aan. Geef ook de hoek θ aan.
b Bereken de massa van het object dat als lens fungeert.
c Wat voor soort object zou deze lens kunnen zijn? Licht je antwoord toe.
A Een aarde-achtige planeet.
B Een zonachtige ster.
C Een sterrenstelsel.
D Een cluster van 1000 sterrenstelsels.