Cyclisch rekenen

Cyclisch rekenen
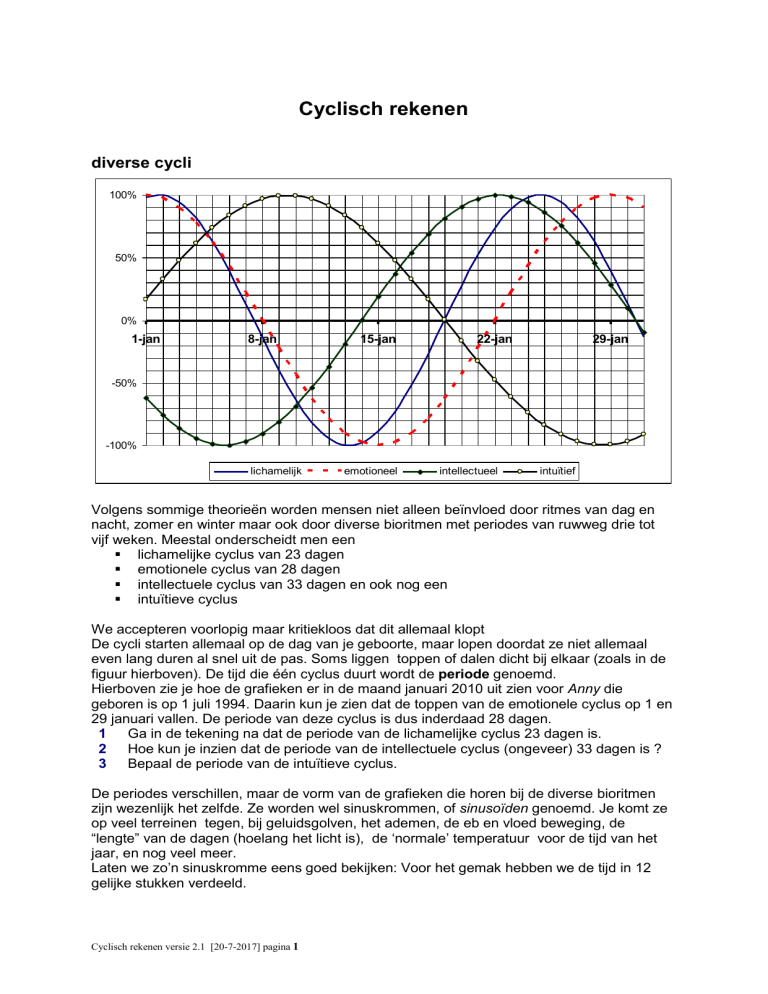
diverse cycli
100%
50%
0%
1-jan
8-jan
15-jan
22-jan
29-jan
-50%
-100%
lichamelijk
emotioneel
intellectueel
intuïtief
Volgens sommige theorieën worden mensen niet alleen beïnvloed door ritmes van dag en
nacht, zomer en winter maar ook door diverse bioritmen met periodes van ruwweg drie tot
vijf weken. Meestal onderscheidt men een
 lichamelijke cyclus van 23 dagen
 emotionele cyclus van 28 dagen
 intellectuele cyclus van 33 dagen en ook nog een
 intuïtieve cyclus
We accepteren voorlopig maar kritiekloos dat dit allemaal klopt
De cycli starten allemaal op de dag van je geboorte, maar lopen doordat ze niet allemaal
even lang duren al snel uit de pas. Soms liggen toppen of dalen dicht bij elkaar (zoals in de
figuur hierboven). De tijd die één cyclus duurt wordt de periode genoemd.
Hierboven zie je hoe de grafieken er in de maand januari 2010 uit zien voor Anny die
geboren is op 1 juli 1994. Daarin kun je zien dat de toppen van de emotionele cyclus op 1 en
29 januari vallen. De periode van deze cyclus is dus inderdaad 28 dagen.
1 Ga in de tekening na dat de periode van de lichamelijke cyclus 23 dagen is.
2 Hoe kun je inzien dat de periode van de intellectuele cyclus (ongeveer) 33 dagen is ?
3 Bepaal de periode van de intuïtieve cyclus.
De periodes verschillen, maar de vorm van de grafieken die horen bij de diverse bioritmen
zijn wezenlijk het zelfde. Ze worden wel sinuskrommen, of sinusoïden genoemd. Je komt ze
op veel terreinen tegen, bij geluidsgolven, het ademen, de eb en vloed beweging, de
“lengte” van de dagen (hoelang het licht is), de ‘normale’ temperatuur voor de tijd van het
jaar, en nog veel meer.
Laten we zo’n sinuskromme eens goed bekijken: Voor het gemak hebben we de tijd in 12
gelijke stukken verdeeld.
Cyclisch rekenen versie 2.1 [20-7-2017] pagina 1
4
Laat zien dat de gunstige en de ongunstige tijd ieder een derde deel uitmaken van de
cyclus.
Met behulp van deze grafiek kunnen we – met een klein beetje rekenwerk – voorspellingen
doen over de diverse cycli
Een voorbeeld. 22 januari 2010 is voor Anny intellectueel gezien een topdag. Wanneer
begint voor haar de ongunstige periode ?
In de grafiek is te zien dat van top naar ongunstig 4 (van de 12) stappen is, dus een derde
periode. De periode van de intellectuele cyclus is 33 dagen, dus na 11 dagen begint voor
Anny een ongunstige periode.
5 Welke datum is dat ?
6 Wanneer begint voor Anny emotioneel gezien een ongunstige periode?
7 Hoe staat Anny er lichamelijk voor op 10 februari ?
8 Hoe sta je er intellectueel gezien voor over vier weken als je nu een topdag hebt ?
Het rekenen op korte termijn is niet zo moeilijk, maar hoe bereken je hoe je ervoor staat over
drie maanden, een jaar of op de eerste dag van je eindexamen ?
9 Ga na hoe je zo’n berekening zou aanpakken.
Een probleem bij dit soort berekeningen is dat we te maken hebben met diverse cycli, de
bioritmen, de maanden en de jaren. Daarbij komt nog bij dat de lengte van de maanden
varieert, en die van de jaren ook nog enigszins (schrikkeljaren). Het is misschien goed om
eenvoudig te beginnen:
10 Iemand heeft op vrijdag een emotioneel dieptepunt. Laat zien dat zowel de
hoogtepunten als de dieptepunten altijd op een vrijdag zullen vallen.
11 Iemand heeft een lichamelijk topdag op zondag. Op welke dag van de week valt de
volgende topdag ?
12 Laat zien dat de intellectuele cyclus elke keer twee dagen ‘opschuift’. Welke richting ?
13 Laat zien dat bij de lichamelijke en intellectuele cyclus altijd alle dagen van de week
aan bod komen als topdag (of als ‘dipdag’ )
Door te letten op je verjaardag, of een andere belangrijke dag met een vaste datum heb je
vermoedelijk wel gemerkt dat deze normaal gesproken één weekdag opschuift, en één
maal in de vier jaar met twee dagen.
14 Laat zien dat een jaar net iets meer is dan 52 weken.
15 Laat zien dat in vier jaar een verjaardag 5 (week)dagen opschuift.
16 Laat zien dat er ruim elf intellectuele cycli in een (gewoon) jaar gaan.
17 Laat zien dat je in een gewoon jaar twee dagen ‘opschuift’ in je intellectuele cyclus.
18 Bereken hoeveel dagen je opschuift (in je intellectuele cyclus) in 4 jaar
19 Iemand heeft vandaag een intellectueel dieptepunt. Hoe is dat over 4 jaar ?
Cyclisch rekenen versie 2.1 [20-7-2017] pagina 2
Modulo, ggd en kgv
Je kunt zeggen dat als je een (gewoon) jaar in weken verdeelt, je één dag overhoudt
We schrijven daarom ook wel :
365/ 7 = 52 rest 1
Die 52 is in dit verband minder belangrijk, het gaat om de rest. Vandaar ook de volgende
notatie :
365 ≡ 1 (modulo 7)
Je kunt vertalen als “Als je in weken denkt is de 365e dag hetzelfde als de 1e “
Hoe kun je bijv. 365 modulo 23 berekenen ?
1. 365/23 = 15,869.. Er passen dus 15 hele cycli in het jaar
2. 15×23 = 345
Dat zijn 345 dagen
3. 365 − 345 = 20
Er zijn dus nog 20 dagen over
Het kan ook anders:
1. 365/23 =15,869..
2. 0,869.. × 23 = 20
Van de laatste cyclus is ca. 87%(0,869..) gedaan
Dus 20 dagen.
Op veel rekenmachines is het ook mogelijk om de breuk
herschrijven als 15
365
automatisch te
23
20
. Je kunt dan goed zien dat de rest 20 is.
23
Voor sommige rekenmachines is er een programmaatje die dit voor je doet.
20
21
22
23
Ga na hoe iemand die vandaag lichamelijk een topdag heeft er over een jaar voorstaat.
Laat zien dat 75 ≡ 3 (modulo 12)
Laat zien dat 70 modulo 24 gelijk is aan 22
Bereken 23 modulo 7.
Modulo rekenen gebruik je (onbewust) vaak bij het rekenen met tijden. Een paar
voorbeelden:
24 Iemand gaat om 21:00 uur (9 uur ’s avonds) naar bed, en slaapt 11 uur aan een stuk.
Hoe laat wordt hij wakker ?
25 Het is nu 20 over tien. Hoe laat is het over 50 minuten ?
26 Een recordpoging begint om 12:00 (’s middags). 57 uur later is het voorbij. Hoe laat is
het dan?
27 Op een digitale klok staat 21:51 Gebruik het begrip modulo om uit te leggen wat de
getallen 21 en 51 betekenen.
Met modulo rekenen kun je als het ware grote sprongen in de tijd doen.(bij cycli)
28 Bereken 365 modulo 33.
29 Laat zien dat na een (gewoon) jaar je intellectuele cyclus twee dagen is verschoven.
30 Hoeveel bedraagt de verschuiving in vier jaar (!).
31 Hoe zit dat met de intuïtieve cyclus ?
32 Iemand zat precies vier jaar geleden lichamelijk in een dal. Hoe is dat nu ?
Optellen en vermenigvuldigen kan bij modulo rekenen heel eenvoudig
33 Ga na dat (2001+102+8793) ≡ 6 (modulo 10)
34 Bereken (handig) (7001+ 702 + 73 +4) modulo 7.
35 Bereken (handig) (15×7001) modulo 7.
36 Bereken (handig) (1234x5678) modulo 10.
Cyclisch rekenen versie 2.1 [20-7-2017] pagina 3
De emotionele cyclus heeft een periode van 28 dagen, dus precies 4 weken.
Een jaar bestaat –zoals we gezien hebben - niet uit een heel aantal weken. Dat is makkelijk
na te rekenen op een rekenmachine, maar kan ook met een beetje hoofdrekenen worden
beredeneerd. Bijvoorbeeld zo:
 350 (=7x50) is een heel aantal weken
 Resteert nog 365−350 = 15 dagen ( of 366−350=16 dagen)
 Dat is geen heel aantal weken
 Een jaar bestaat dus niet uit een heel aantal weken
37 Ga na (zonder rekenmachine) of 1827 deelbaar is door 7
38 Ga ook na (zonder rekenmachine) of 1857 deelbaar is door 7
Soms kun heel snel de deelbaarheid bepalen
39 Noem drie even getallen. (getallen die deelbaar zijn door twee.)
40 Hoe kun je snel aan een getal zien of het even is ?
41 Noem drie getallen die deelbaar zijn door 5.
42 Noem drie getallen die deelbaar zijn door 3.
43 Is het getal 1234567891011 deelbaar door 3 ?
Om na te gaan of een getal deelbaar is door 3 bestaat een simpele regel
 Tel alle cijfers waaruit het getal bestaat bij elkaar op
 Ga na of dit getal (de som der cijfers) deelbaar is door 3
44 Tel de cijfers van 1234567891011 bij elkaar op.
45 Ga na of 4321 deelbaar is door 3.
46 Ga na hoe je het optellen van de cijfers nog wat kunt vereenvoudigen.
De achtergrond van dit ‘trucje’ is dat 10, 100, 1000 etc. allemaal modulo 3 gelijkwaardig zijn
aan 1.
10 ≡ 100 ≡ 1000≡…≡ 1 (modulo 3)
Modulo 3 zijn dus bijv 40, 400, en 4000 allemaal gelijkwaardig aan 4.
47 Bereken 4321 (4000+300+20+1) modulo 3.
48 Is 4321 (dus) deelbaar door 3 ?
49 Bereken 200820092010 modulo 3.
Het bepalen of een getal deelbaar is door 9 gaat ook prima op “deze manier”
50 Is het getal 1234567891011 deelbaar door 9 ?
51 Vroeger was het nummer op bankbiljetten altijd deelbaar door 9. Ga na of dat nog zo
is.
52 Leg uit waarom deze aanpak werkt bij 3 en 9, en bijv. niet bij 7.
Het getal 60 en veelvouden daarvan zoals 180 en 360 kom je vaak tegen bij hoeken en
tijden. In sommige culturen werd ook gewerkt met een jaar van 360 dagen. Achtergrond
hiervan is dat deze getallen flink wat delers hebben. Iets dergelijks geldt trouwens voor 12 en
24. Zo heeft het getal 12 zes delers: 1, 2, 3, 4, 6 en 12
53 Bereken alle delers van 60.
54 Bereken alle delers van 24.
55 Bereken alle delers van 360.
Tegenover getallen met veel delers staan getallen die maar twee delers: priemgetallen.
Voorbeelden zijn 5, 7, 13. Ze zijn alleen deelbaar door 1 en zichzelf.
56 Ga na welke van de volgende getallen priem zijn: 23; 28; 33; 37
Cyclisch rekenen versie 2.1 [20-7-2017] pagina 4
24 en 60 hebben verschillende delers gemeenschappelijk. De grootste daarvan is 12.
We noemde dit de grootste gemeenschappelijke deler, afgekort ggd.
ggd(24;60) =12
Wanneer je de getallen opvat als aantallen uren, kun je zeggen dat 12 uur (een half etmaal)
een goede maateenheid is. 24 uur is dan twee eenheden, en 60 uur is 5 eenheden.
De ggd kan o.a. van pas komen bij het vereenvoudigen van breuken.
24
60
210
Vereenvoudig
510
57 Vereenvoudig
58
De ggd kan soms ook verhelderend werken bij omgerekende maten
In een wat knullig uit het Engels vertaalde reisgids werden bij een plaatsje twee
bezienswaardigheden genoemd, een op 8045 meter afstand en een op 11263 meter
afstand van het dorp.
59 Enig idee wat er aan de hand zou kunnen zijn ?
60 Zoek uit hoeveel meter een Engelse (land)mijl is, en los het ‘raadsel’ op.
In dezelfde gids wordt ook gesproken over heuvels met een hoogte van ca. 366 en ca. 671
meter.
61 Probeer te achterhalen welke maateenheid oorspronkelijk gebruikt is.
Zonder kennis van de Engelse maten kunnen we in ieder geval proberen ggd (366;671) te
bepalen. Dat kan o.a. op de volgende manier.
 Noem g =ggd (366;671)
 671 en 366 zijn deelbaar door g, dus het hoogte verschil 305 [=671−366] ook
 Dus g = ggd(366;305)
 We gebruiken weer het verschil : 365 − 305 =61
 Dus g = ggd(61;305) = 61 (want 305 =5×61)
De gemeenschappelijk maateenheid is dus 61 meter (200 feet)
De ene heuvel is (ongeveer) 6 maal zo hoog [366/61 =6], dus 6 x 200 ft = 1200 ft
De andere is (ongeveer) 11 maal zo hoog [671/61=11], dus 11 x 200 ft = 2200 ft
De achtergrond van deze aanpak is het al eeuwenoude algoritme van Euclides.
We gebruiken een zelfde aanpak om ggd(280;945) te bepalen. We noemen dit weer g
62 Noem drie getallen (kleiner dan 945) die deelbaar zijn door g.
63 Bereken 945 modulo 280 .
64 Leg uit dat ggd(280;945).=ggd(280;105)
65 Bereken ggd(280;105)
66 Bereken met het algoritme van Euclides ggd(24;60)
Bij de bepalingen over de afmetingen van een tennisveld komen de volgende maten voor:
2377,44 cm ; 1097,28 cm en 822,96 cm
Probeer te achterhalen wat de gemeenschappelijk maateenheid is.
Om snel een ggd te berekenen van twee (hele) getallen kun je gebruik maken van
programmaatjes. Op sommige rekenmachines is de de ggd beschikbaar onder de Engelse
afkorting (gcd)
Cyclisch rekenen versie 2.1 [20-7-2017] pagina 5
67 Bereken ggd(23; 37)
68 Waarom had je het resultaat kunnen voorspellen ?
Bij de emotionele cyclus (periode 28 dagen) is een topdag altijd de zelfde dag van de week.
Als dinsdag je topdag is geldt het zelfde voor de volgende cyclus (28 dagen= 4 weken later)
Bij bijv de lichamelijke cyclus (periode 23 dagen) ligt dat anders. Als je topdag dit keer op
een dinsdag valt, is het volgende keer een donderdag. Immers 23 modulo 7= 2.
Zoals je makkelijk kunt narekenen valt na 7 periodes de topdag weer op dinsdag. We
zeggen dat beide cycli (lichamelijke cyclus en de weekcyclus) weer gelijk lopen
Zeven periodes zijn 7× 23 dagen = 23 × 7 dagen = 23 weken
69 Bereken na hoeveel dagen de intellectuele cyclus (33 dagen) en de weekcylcus weer
gelijk lopen
70 Na hoeveel dagen lopen de lichamelijke cyclus en de intellectuele cyclus weer gelijk ?
In bovenstaande gevallen kon je gewoon de periodes met elkaar vermenigvuldigen, maar zo
makkelijk is het niet altijd. Kijk eens naar de volgende tabel:
0
1
2
3
4
5
6
7
8
9
10
0
24
48
72
96
120
144
168
192
216
240
0
60
120
180
240
300
360
420
480
540
600
Je kunt bijvoorbeeld denken aan twee lampen, waarvan er één elke 24 minuten een keer
knippert, en de andere om het uur. Ze starten gelijk, wanneer knipperen ze voor het eerst
weer gelijk ? Al na 120 minuten, want 120 = 5×24 en 120 =2×60
We noemen 120 het kleinste gemeenschappelijke veelvoud van 24 en 60 :
kgv(24;60) = 120
Dat het kgv in dit geval zo klein is ( en niet bijv 24×60 = 1440) heeft alles te maken met het
ggd. Zoals eerder berekend geldt ggd(24,60) =12
71 Het kgv is hier gelijk aan 10 keer het ggd. Verklaar dat.
Er zijn allerlei manieren om het kgv te berekenen. Zie daarvoor de volgende pagina
Probeer de onderstaande vragen zo handig mogelijk op te lossen.
72 Bepaal kgv(12;30)
73 Bepaal kgv(7;28)
74 Bepaal kgv(30;365)
75 Bepaal kgv(28;366)
76 Bepaal kgv(28;33)
77 Bepaal kgv(23;28;33)
78 Bereken de periode van de drie bioritmes (lichamelijk, emotioneel en intellectueel)
samen. Hoeveel jaar is dat ongeveer?
79 De eb en vloed beweging heeft een periode van ruim 12 uur, zeg 12,4 uur. Stel dat
vandaag hoogwater precies om 13:00 uur valt. Hoe lang duurt het voordat dit weer
gebeurt?
Een bekende toepassing van het kgv is het gelijknamig maken van breuken (om ze op te
tellen of te vergelijken)
1
1
en
gelijknamig.
24
60
1 1
Bereken kgv( ; ) Tip: gebruik de gelijknamige breuken
24 60
80 Maak de breuken
81
82 Bereken ggd(24,60).
Cyclisch rekenen versie 2.1 [20-7-2017] pagina 6
1 1
a b
83 Formuleer een vermoeden over kgv( ; ) en ggd(a,b).
Hoe bereken je het kgv (kleinste gemeenschappelijke veelvoud) van twee getallen?
Er zijn diverse aanpakken
I proberen
Wanneer de getallen niet te groot zijn, of veel gemeenschappelijk hebben zie je vaak snel
wanneer twee reeksen elkaar ontmoeten: Bijv kgv(30,70):
30; 60; 90 ; 120; 150; 180; 210 ( = 3 x70) Sneller is natuurlijk 70, 140, 210 (=7x30)
II met behulp van verschuivingen
Ook een stapsgewijze aanpak, maar wat minder strak.
Stel je voor twee lampjes, een rode die knippert elke 910 seconden,en een groene die
knippert om de 1190 seconden. Om 0:00:00 knipperen ze samen, hoelang duurt het voordat
ze weer samen knipperen ?
1. De eerste keer knippert het groene lampje 280 (1190-910) sec te laat
2. Daar komt elke keer 280 sec bij.
3. Na 3 keer knipperen loopt het groene lampje 840 sec. achter op het rode, maar dat
is het zelfde als 70 sec. vóór. Immers over 70 sec. ( 910−840 ) knippert het rode
lampje weer !
4. Na 4×3 (=12) maal knipperen is de voorsprong 4×70 =280 sec.
5. Dus na 13 keer loopt het weer gelijk.
6. 13 × 910 = 15470
III met behulp van de ggd
Je bepaalt eerst de ggd van beide getallen. Als dat 1 is kun je gewoon beide getallen met
elkaar vermenigvuldigen, anders moet je corrigeren. Als voorbeeld: kgv(910;1190)
1. ggd(910;1190) = 70
2. 910 = 13 ×70
3. 1190 = 17 ×70
4. kgv(13;17) = 13×17=221 [13 en 17 hebben niets gemeenschappelijk !]
5. kgv(910;1190) =221×70= 15470 [ = 13×1190 = 17×910 ]
Een variant hierop gebruikt: kgv( a; b) 
a b
ggd( a; b)
Dus kgv(910;1190) = 1190×910 /70 = 15470.
IV met behulp je rekenmachine
Op sommige rekenmachines kun je het kgv laten berekenen. De Engels afkorting is lcm.
Daarnaast zijn er o.a. op internet alle programmaatjes beschikbaar.
Met wat kleine aanpassingen zijn deze methoden ook te gebruiken om het kgv te berekenen
van getallen die niet (allemaal) geheel zijn. Een aanpak is beide getallen met een geschikt
getal te vermenigvuldigen, en naderhand te corrigeren.
Bijvoorbeeld kgv(0,6 ; 1,4) = 0,1×kgv(6;14) = 0,1× 42= 4,2
Controle: 4,2 = 7×0,6 = 3×1,4.
Cyclisch rekenen versie 2.1 [20-7-2017] pagina 7
kalenders
Hierboven zie je een kalender voor de maand december voor de jaren 2003, 2009 en 2015
84 Hoe kun je narekenen dat de kalender het hele jaar 2015 gelijk is aan die voor 2009?
85 Leg uit waarom de kalenders van 2003 en 2009 niet identiek zijn.
Als je de kalender van 28 jaar geleden gebruikt zit je ‘altijd’ goed. Dit is als volgt in te zien
Bij kalenders heb je te maken met twee cycli
 Een cyclus van vier jaar (3 gewone en een schrikkel- ), oftewel 1461 dagen
 Een cyclus van een week oftewel 7 dagen
86 Berekenen kgv(7;1461)
87 Hoeveel jaar is dit aantal dagen ? (Hou rekening met schrikkeljaren!)
De lengte van ons jaar is gebaseerd op de beweging van de aarde om zon.
Een zonnejaar bestaat eigenlijk uit ca. 365,2422 dagen, vaak wordt dit afgerond op 365,25
dagen. De kalenders in Europa waren eeuwenlang gebaseerd op 365,25 dagen (eens in de
vier jaar een schrikkeljaar), maar dat is dus eigenlijk iets te lang
88 Bereken hoeveel minuten een jaar te lang duurde
89 Ga na dat na duizend jaar het verschil meer dan een week bedraagt
Om deze afwijking te corrigeren, werd in 1582 op last van paus Gregrorius XIII

De ‘kalender’ tien dagen voorgezet. Na donderdag 4 oktober volgde vrijdag 15
oktober 1582

Het systeem van schrikkeljaren aangepast, zodat elk jaartal dat deelbaar was
door 100 voortaan geen schrikkeljaar is, behalve als het ook door 400 te delen is.
Dat betekent dat bijvoorbeeld 1600, 2000 schrikkeljaren zijn, maar 1700, 1800,
1900 en 2100 niet.
90 Laat zien dat het gemiddelde kalenderjaar voortaan 365,2425 dagen duurt.
91 Hoeveel scheelt dan met het gemiddeld zonnejaar van 365,2422 dagen ?
Niet alle kalenders zijn gebaseerd op de zon. Er zijn er ook veel die de maancyclus als
uitgangspunt nemen. De maanstand heeft een periode van ca. 29,5306 dagen, wat vaak
afgerond wordt op 29,5 dagen. Bij een op de maandstand gebaseerde kalender is de
verdeling in jaren ondergeschikt aan die in maanden. Een voorbeeld hiervan is de
islamitische tijdrekening. Een islamitisch jaar bestaat uit exact 12 maanden van 29,5306
dagen. In de praktijk bestaan de maanden (min of meer afwisselend) uit 29 of 30 dagen
92 Uit hoeveel dagen bestaat het islamitisch jaar ?
93 Het begin van de Ramadan is gebaseerd op de stand van de maan. Deze datum
verschuift elk jaar een aantal dagen naar voren. Hoeveel ongeveer ?
Cyclisch rekenen versie 2.1 [20-7-2017] pagina 8
De islamitische tijdrekening begint – volgens de meeste interpretaties – op donderdagavond
15 juli 622 nC bij zonsondergang.
94 Bereken in welk jaar van de islamitische tijdrekening we nu zitten
Kijk eventueel op http://www.phys.uu.nl/~vgent/islam/islam_nl.htm ter controle.
Vaak werden zowel zon als maan gebruikt als richtsnoer voor de kalender.
In Mesopetanië (het huidige Irak) werd door de Babyloniërs ca. 3000 jaar geleden gewerkt
met maanden van 20 of 30 dagen, en 12 of 13 maanden per jaar.
De dertiende maand werd oorspronkelijk ingevoegd “wanneer nodig”, maar op een gegeven
moment ging met gebruik maken van de waarneming dat na 19 jaren zon en maan weer 'in
de pas' liepen.
95 Laat zien dat na19 jaar de zon en maan inderdaad weer in de pas lopen.
96 Hoe veel maanmaanden is dit ?
In het westen speelt de maan ook nog een rol bij de bepaling van de paasdatum. Er zijn
diverse formules ontwikkeld voor de berekening van de datum van Pasen. Daarbij speelt
het modulo 19 -rekenen een belangrijke rol.
97 Bereken de waarde van het huidige jaartal modulo 19.
Een zeer bijzonderde tijdrekening werd gebruikt door Maya’s
in Midden Amerika.
Zij gebruikte o.a. de “lange tijdrekening”, die als volgt was
opgebouwd:
 Winal (periode van 20 dagen)
 Tun ( 18 Winal)
 K’atun (20 Tun)
 B’ak’tun (20 K’atun)
98 Laat zien dat een Tun bijna een jaar duurt
99 Bereken hoeveel jaar een B’ak’tun duurt.
Het startpunt van deze tijdrekening komt (vermoedelijk)
overeen met een dag in het jaar 3114 vC. Volgens
berekeningen komt dan 13:0:0:0:0 (13 B’ak’tun) later overeen
met 21 december 2012
100 Ga na of dit enigszins kan kloppen.
Om makkelijker met tijden en datums te kunnen rekenen geeft een spreadsheet als Excel ze
(intern) weer als getal: hoeveel dagen er zijn verstreken sinds een bepaald tijdstip.
Zie de tabel:
datum en tijd
1-1-2000 0:00
1-1-2000 12:00
24-12-2008 10:19
1-1-2010 0:00
Cyclisch rekenen versie 2.1 [20-7-2017] pagina 9
getal
36526,000000
36526,500000
39806,430237
40179,000000
seconden
3155846400
3155889600
3439275573
3471465600
101 Ga na in welk jaar het beginpunt van deze telling ligt
102 29-02-1900 krijgt van Excel de getalswaarde 60. Waarom is dit onjuist ?
103 Beschrijf hoe je het aantal seconden berekent op basis van de getalswaarden.
104 Bereken hoeveel seconden een jaar ongeveer duurt
Bij de traditionele Chinese kalender krijgt elk jaar twee namen:
 Een verwijzing naar 10 verschillende Goden. jia, yi, bing, ding,…,gui
 Een verwijzing naar 12 verschillende dieren. rat, os, tijger, konijn,.. , hond,varken
1
2
3
4
5
6
7
8
9
10
jia
yi
bing
ding
wu
ji
geng
xin
ren
gui
1
2
3
4
5
6
7
8
9
10
11
zi
chou
yin
mao
chen
si
wu
wei
shen
yo
xu
rat
os
tijger
konijn
draak slang
aap
haan
paard schaap
hond
12
hai
varken
105 Laat zien dat er 120 combinaties met deze namen gemaakt kunnen worden
De naamgeving is echter niet (jia;zi) ,(jia;chou), (jia;yin) etc, maar (jia;zi ,(yi;chou), (bing;yin)
etc. Nadat alle goden aan bod zijn geweest, zijn er nog twee dieren over. De naamgeving
gaat (dus) verder met (jia; xu), (yi;hai), (bing;zi) etc.
106 Laat zien dat de Chinese kalender een cyclus heeft van 60 jaar
107 Welke combinaties worden niet gebruikt ? (geef tenminste twee voorbeelden)
====
Cyclisch rekenen versie 2.1 [20-7-2017] pagina 10