u = u(P,v,T) = interne energie = de som van alle soorten energie

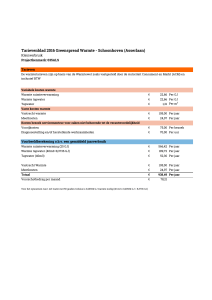
Samenvatting Technische Thermodynamica
Thermodynamica
Thermodynamica = het onderdeel van de natuurkunde dat zich bezighoudt met de effecten
van temperatuur, druk en veranderingen van volume van een fysisch systeem op
macroscopische schaal. Samengevat houdt thermodynamica zich bezig met de omzetting van
warmte-energie in arbeid en omgekeerd. De snelheid waarmee dat gebeurt is het vermogen.
De kunst is om ingewikkelde dingen als enthalpie uit te rekenen met meetbare variabelen,
zoals druk en temperatuur.
Bij het maken van sommen kijk je altijd naar een systeem. Dit systeem wordt afgebakend van
zijn omgeving door de systeemgrens. Deze systeemgrens kan zowel fysiek als denkbeeldig
zijn. Aan de systeemgrens kunnen 3 soorten transporten plaatsvinden:
Soort transport
Materie (massa, inclusief de energie die
in die massa opgeslagen zit, zoals
kinetische energie, zwaarte-energie en
potentiële energie)
Warmte (energie in de vorm van warmte)
Volume (Materialen die vervormen
krijgen een groter volume bij een gelijk
aantal atomen, dus dan stop je er volumearbeid in)
Indien wel/Indien niet
Open/gesloten
Diathermisch/Adiabatisch
Vervormbaar/Star
Indien er sprake is van zowel een gesloten als een adiabatisch systeem, dan spreken we van
een geïsoleerd systeem.
Belangrijke grootheden:
Grootheid
Arbeid
Warmte
Volume
Entropie
Interne energie
Enthalpie
Symbool
W
Q
V
S
U
H
Eenheid
Nm
J
m3
J/K
J
J
HOOFDLETTER = normale vorm, bijv. Q in J
kleine letter = gedeeld door massa, bijv. q = Q/m in J/kg
Fluctie = gedeeld door tijd, bijv. = W/t (= verm.) in J/s
Tekenafspraak: Arbeid of warmte die het systeem ingaat is positief
2 soorten arbeid:
1. Volume-arbeid: Zorgt voor de verplaatsing van materie
2. As-arbeid: Zorgt voor de rotatie van materie
Behoudswetten:
1. Wet van behoud van energie (of enthalpie)
2. De entropie (niet-bruikbare energie) van een geïsoleerd systeem dat niet in evenwicht
is zal altijd stijgen (warmte stroomt alleen van warm naar koud en niet andersom).
Deze wet verklaart ook dat we nuttige energie (dus het tegenovergestelde van
entropie) kunnen winnen uit een systeem dat niet in evenwicht is. Zo kan er nuttige
energie gewonnen worden uit water dat van hoog naar laag valt, of elektronen die van
de - pool naar de + pool stromen, of luchtdruk die er voor zorgt dat moleculen van
plaatsen met hoge luchtdruk wegstromen naar plaatsen met lage luchtdruk.
3. Alle processen komen tot stilstand als het absolute nulpunt genaderd wordt.
Postulaten: (Stellingen die niet bewezen hoeven te worden)
1. Macroscopisch evenwicht hangt alleen af van U, V en N
2. Entropie bepaalt de mate van macroscopisch evenwicht, dus entropie (S) is een functie
van U, V en N, ofwel: S (U,V,N)
3. Er kan extra entropie aan een systeem toegevoegd worden door meer interne energie
toe te voegen. De entropie als functie van U is een monotoon stijgende, continue en
differentieerbare functie
4. Als S = 0, dan T = 0 (absolute nulpunt, 0 K). ΔS = Q/T
We maken onderscheid tussen extensieve (veranderen mee met de situatie) en intensieve
(veranderen niet mee met de situatie) variabelen. In de thermodynamica moet je er voor
zorgen dat je zoveel mogelijk met intensieve variabelen rekent. Er zijn een aantal paren:
Extensief
s (entropie)
v (volume)
n (aantal deeltjes)
Intensief
T (temperatuur)
-P (druk met minteken)
μ (chemische potentiaal)
Veelgebruikte processen:
 Een isobarisch proces: druk is constant
 Een isochorisch proces: volume is constant
 Een isothermisch proces: temperatuur is constant
 Een isentropisch proces: bij constante entropie
 Een adiabatisch proces: zonder winst of verlies van warmte
Entropie = de warmte gedeeld door de temperatuur. Het is een maat voor de hoeveelheid
chaos. In een gesloten systeem zal de entropie steeds groter worden.
Interne energie = u = u(P,v,T) = de som van alle soorten microscopische energie, zoals
kinetische energie, vanderwaalsenergie en chemische energie
 u 
 u 
 u 
Totale differentiaal van u: du    ds    dv    dn
 s  v ,n
 v  s ,n
 n  s ,v
Hierbij geldt:
 u 
    T (Temperatuur)
 s  v ,n
 u 
     P (Druk met minteken)
 v  s ,n

 u 
    (Chemische potentiaal)
 n  s ,v
Invullen in du: du  T * ds  P * dv   * dn
Verschillende soorten energie:
Naam
Symbool
Formule
Differentiaal
Interne
energie
Enthalpie
u (s,v)
u
du  T * ds  P * dv   * dn
h (s,P)
h=u+
P*V
dg  T * ds  v * dP   * dn
Helmholtz
Vrije
energie
f (T,v)
f = u – T*s
df   s * dT  P * dv   * dn
Gibbs
Vrije
energie
g (T,P)
g = u – T*s
+ P*V
dg   s * dT  v * dP   * dn
Wordt gebruikt
voor:
Interne energie in
gesloten systemen
Open systemen bij
constante druk (dan
vervallen de laatste
twee termen;
daarom rekent
enthalpie ook veel
gemakkelijker dan
interne energie)
Het bepalen van de
maximaal
verkrijgbare nuttige
arbeid uit een
gesloten
isothermisch
systeem.
Dan is de helmholtz
energie op een
minimun, dus df = 0
Het bepalen van de
maximaal
verkrijgbare nuttige
arbeid uit een open
isothermisch en
isobarisch systeem.
Dan is de Gibbs
energie op een
maximum, dus dg =
0.
Met behulp van de 4 Maxwell-vergelijkingen kunnen we alle potentialen omschrijven naar
meetbare grootheden:
 T   P 
  = 
 v s  s v
 s   P 
  = 
 v T  T v
 T   v 
  = 
 P s  s P
 s 
 v 
  =  
 P T  T P
Meetbare grootheden:
Symbool
1  v 
=  
v  P T
1  v 
=  
v  T P
 h 
 s 
cP =    T  
 T  P
 T P
Tv 2
 u 
 s 
 T 
  Cp 
cV  

 T  v
 T v
IPC 
1  P 

*
 
P  T  v ,n P *
Naam
Isothermische compressibiliteitscoëfficiënt
Volumetrische uitzettingscoëfficiënt
Soortelijke warmte met constante druk
Soortelijke warmte met constant volume
Isocohorische drukcoëfficiënt
Hierbij komen de volgende rekenregels goed van pas (LET HIERBIJ OP DE
VARIABELEN DIE JE CONSTANT HOUDT!):
Regel
y x z
* *
 1
x z y
y
1

x  x 
 
 y 
y
y z

x x
z
Naam
Min 1 regel
Omkeerstelling
Kettingregel
Een ideaal gas is een gas dat zich gedraagt volgens de formule PV = NRT. In werkelijkheid
bestaan geen ideale gassen, maar veel gassen kun je wel benaderen met dit ideale gasmodel.
Voor een ideaal gas gelden de volgende dingen:
 PV = NRuT Met universele gasconstante Ru
 Pv = RT
Met stofafhankelijke gasconstante R
 α = 1/P
 β = 1/T
 IPC = 1/T
 cp-cv = R
(LET OP: R = stofafhankelijke gasconstante, en niet de universele
gasconstante)
 du = cv*dT
 dh = cp*dT
 P*vγ = constant
met v = RT/P en γ = cp/cv
Een incompressible liquid is een vloeistof waarvan het volume niet verandert onder invloed
van druk of temperatuur. Hierbij gelden de volgende dingen:
 v = constant, dus dv = 0
 α=0
 β=0
 c = cp = cv
 IPC = 0
 du = cp*dT
 dh = cp*dT + v*dP
De combinatie van temperatuur en druk bepaalt wanneer een stof begint te smelten of te
verdampen. Zo heeft water met een druk van 101,42 kPa (atmosferische druk) een kookpunt
van 100°C, maar water met een druk van 198,67 kPa heeft een kookpunt van 120°C.
T-s diagram
Engels
Melting
Sublimation
Desublimation
Freezing
Vaporizaton
Condensation
Latent heat
Solid
Liquid
Vapor
Saturated
Compressed
liquid
Saturated liquid
Nederlands
Smelten
Sublimeren
Desublimeren/rijpen
Bevriezen
Verdamping
Condenseren
Energie die nodig is om een
vloeistof te laten verdampen
Vaste stof
Vloeistof
Gas
Verzadigd
100% vloeistof
Grens tussen 100% vloeistof en
twee-fasengebied
Saturated mixture Half vloeistof, half gasfase
Saturated vapor
Grens tussen 100% gasfase en
twee-fasengebied
Superheated
100% gasfase
vapor
Fig.1: Een T-s diagram: Tijdens de fase-overgang blijven temepratuur en druk constant.
Een H-s diagram wordt ook wel een Mollier diagram genoemd.
Als een stof in het 2-fasengebied zit, is hij bezig over te gaan van de vloeistoffase naar de
gasfase, of andersom. Tijdens dit proces zijn de temperatuur en druk steeds constant; met
andere woorden: Bij elke gegeven druk hoort een bepaalde overgangstemperatuur. In dit
gebied kun je tevens de dampfractie x uitrekenen. Dit is het aantal dampdeeltjes gedeeld
door het totaal aantal deeltjes. Deze gebruik je onder andere voor het bepalen van de hwaarde, waarbij h = hf + x*(hg-hf). Buiten het 2-fasengebied is x niet gedefinieerd (dus x is
dan ook géén nul!).
De eerste hoofdwet van de thermodynamica:
n
n
P 1 2
E
1
 i  Q  W   (hi  vi 2  gz i ) * m i  Q  W
  (ui  i  vi  gz i ) * m
t
i 2
2
i 1
i 1
Gesloten systemen:
U2-U1 = Q + W or
Steady
flow
dU = dQ + dW
system
N
.
(tijdsonafhankelijk):
.
2
  (hi  1 vi  g z i )mi  Q  W shaft
2
i 1
Cyclisch proces:
Bernoulli: P 
 dq   dw  0
1 2
v  gz  const .
2
Steady-flow proces met massabehoud:
 in  m
 out  1v1 A1   2 v2 A2
m
(LET OP: Hier is “v” de snelheid!)
De tweede hoofdwet van de thermodynamica:
Reversible process:
Cyclic process:
dS 
dS 
dQ
T
or ( s 2 - s1 ) 
dQ
and dW= -PdV
T
Inequality of Clausius:
dq
 T 0
Exergy.
Open system:
exergy =  h - h0  - T0  s - s0 
Closed system:
exergy  u1  u0   T0 (s1  s0 )
Compressor:
Turbine:
isentropic =
isentropic =
 h isentropic
 h actual
h actual
hisentropic
.
q
T
Belangrijke apparaten in de thermodynamica:
Naam
Pomp
(Druk van
vloeistoffen
verhogen;
zet arbeid
om in
enthalpie)
Compressor
(Druk van
gassen
Verhogen;
zet arbeid
om in
enthalpie)
Turbine
(Druk
verlagen; zet
enthalpie om
in arbeid,)
Nozzle
(Zet
enthalpie om
in Ek)
Boiler
(Temp.
Verhogen;
Zet warmte
om in
enthalpie)
Condensor
(Temp.
Verlagen;
Zet
enthalpie om
in warmte)
Mixer
Open
Voedingswater
Symbool
1e hoofdwet (afleiding kennen!)
(behoud van energie)
rendement
W  (h2  h1 ) * m
isentropic =
 h isentropic
 h actual
W  (h2  h1 ) * m
isentropic =
 h isentropic
 h actual
W  (h1  h2 ) * m
isentropic =
h actual
hisentropic
1 2
1 2
m * (h1  v1 )  m * (h2  v 2 )
2
2
Met m  vA (v = snelheid!!!)
 * h1  Q  m
 * h2
m
 * h1  m
 * h2  Q
m
 2  h1 * m
1
h2 * m
 2  h1 * m
1
h2 * m

v2
2
v2 s
2
heater
LET OP: Een adiabatisch proces betekent dat Q =0, maar dit betekent absoluut niet dat Tin
en Tuit gelijk zijn. Zo kan het best dat bij een adiabatische nozzle de inlaattemperatuur 200°C
is en de uitlaattemperatuur 150°C. Dit temperatuurverschil wordt veroorzaakt doordat
enthalpieverlies optreedt ten gevolge van de hogere eindsnelheid (wet van energiebehoud).
TIP: In een gesloten starre tank blijft het specifiek volume gelijk.
TIP: Goed oefenen met vragen over nozzles. Ook de warmtewisselaar van 9,5 bekijken.
Cp
1
NOG OP TE ZOEKEN: Waar komt de volgende formule vandaan? ds 
dT  R * dP
T

LET OP: Soms is de druk “gage” of “”gemeten” gegeven. Dit betekent dat er ergens een
drukmeter zit die het drukverschil met de atmosfeer meet. Dit betekent dus dat de werkelijke
druk op dat moment 1 atmosfeer hoger ligt!
Stromingsleer
Bernoulli met de verlliesterm:
1
1
L 1
v 2 2  gz 2  P2  v1 2  gz1  P1   * f * * ( v 2 )
2
2
D 2
Hierbij is f de frictiefactor. Deze kun je bepalen met behulp van het Reynouldsgetal
(afgekort als Re).
D*v
 Re 
D = diameter; v = snelheid; ν (nu; kinematische viscositeit) = μ/ρ,

μ is dynamische viscositeit
64
 Voor Voor Laminaire stromingen (Re < 2300) geldt: f 
Re
k
 turbulente stromingen (Re > 2300) moet de relatieve ruwheid
bekend zijn. Hierin is
d
k de ruwheidsnorm van het materiaal waarvan de buis gemaakt is. Met
productiesystemen heette dit de oppervlakteruwheid Ra.
1
Luchtweerstand auto’s: Fw  C w * A frontaal *  lucht * * v 2
2
Rolweerstand auto’s: Fw,rol   * Fn
1
Liftkracht vliegtuigen: FL  C L * Avleugel *  lucht * * v 2
2
1
Luchtweerstand vliegtuigen: FD  C D * Avleugel *  lucht * * v 2
2