Hoofdstuk 2 De sinus van een hoek

Hoofdstuk 2 De sinus van een hoek
2.1 Hoe hoog zit m’n ventiel?
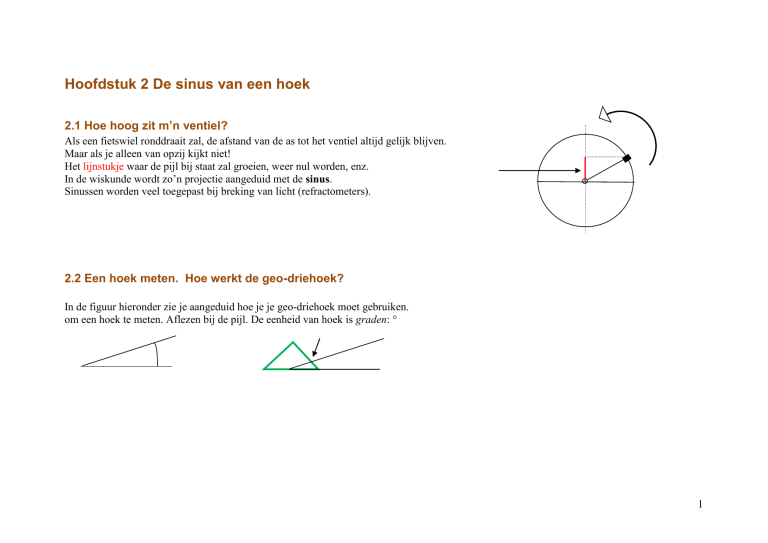
Als een fietswiel ronddraait zal, de afstand van de as tot het ventiel altijd gelijk blijven.
Maar als je alleen van opzij kijkt niet!
Het lijnstukje waar de pijl bij staat zal groeien, weer nul worden, enz.
In de wiskunde wordt zo’n projectie aangeduid met de sinus.
Sinussen worden veel toegepast bij breking van licht (refractometers).
2.2 Een hoek meten. Hoe werkt de geo-driehoek?
In de figuur hieronder zie je aangeduid hoe je je geo-driehoek moet gebruiken.
om een hoek te meten. Aflezen bij de pijl. De eenheid van hoek is graden: °
1
2.3 De sinus (definitie)
(0,1)
Rechts zie je een cirkel waarvan de straal 1 is.
De sinus van een hoek is de verticale projectie van de voerstraal in de eenheidscirkel.
α
De hoek is aangegeven met het boogje.
Het lijnstukje is de sinus. De afkorting van sinus is sin. Dus sin() betekent: de sinus van
hoek . (spreek uit: alfa)
Zie ook de applet:
(1,0)
(-1,0)
http://www.walter-fendt.de/m14nl/sincostan_nl.htm of http://www.ies.co.jp/math/java/samples/sinBox.html
(0,-1)
2
2.4 sinus: het gebruik van je rekenmachine
Zorg ervoor dat de rekenmachine met graden ° (engels:
degrees) werkt.
Casio fx-82MS : MODE MODE 1
Afhankelijk van het type rekenmachine moet je eerst de
hoek intypen en daarna de sin-toets of andersom.
zo vind je: sin(30°)= 0,5
Je rekenmachine kan ook de hoek vinden als de sinus
bekend is:
sin() =0,32   = 19°
Hiervoor gebruik je de SHIFT , de INV of de 2ndF toets.
D
3
oefensommen hoofdstuk 2
2.4.1
Maak de tabel kompleet

sin()
12 °
89°
0,13
-0,73
Bereken met je rekenmachine
a. sin(24°)=
b. sin(156°)=
c. Teken de hoeken in de eenheidscirkel en
verklaar de uitkomst van a. en b.
2.4.2
Bereken  met je rekenmachine
a. sin() = 0,36   =
b. sin() = -0,61   =
Geef van a. en b. in de eenheidscirkel sin() en  aan.
4
2.4.3
Bereken  met je rekenmachine
a. sin() = 1   =
b. sin() = -1   =
c.
Geef van a. en b. in de eenheidscirkel sin() en  aan.
5
Hoofdstuk 3. Breking van licht.
3.1 Wat is breking?
Een lichtstraal, die een grensvlak tussen twee stoffen passeert, verandert van richting. De deze
richtingsverandering is het gevolg van snelheidsverschillen. Bijvoorbeeld: licht gaat in lucht sneller dan in
water.
Je kunt dit vergelijken met een auto die van de weg raakt. De richting van een auto die in zand terecht komt
verandert. Het rechterwiel is eerst in het zand, het linkerwiel gaat dan (even) sneller!
lucht
water
zand
6
3.2 Invalshoek, brekingshoek.
In de figuur hiernaast zie je een lichtstraal die van lucht naar glas gaat en daarna weer naar
lucht. Op de plaats waar de lichtstraal het glas binnenkomt is een loodlijn getekend. Een
loodlijn op een vlak wordt ook wel een normaal genoemd.
De invalshoek i is de hoek tussen de invallende lichtstraal en de normaal.
De brekingshoek r is de hoek tussen de gebroken lichtstraal en de normaal.
De invallende lichtstraal wordt ook weerkaatst. De terugkaatshoek is gelijk aan de
invalshoek.
Geef zelf in de figuur aan de drie hoeken aan: i , r en t
Hieronder zie je de drie hoeken.
lucht
water
7
3.3 De wet van Snellius.
a. Breking naar de normaal toe.
Breking naar de normaal toe betekent: na breking maakt de lichtstraal een kleinere hoek met de normaal.
Dus: r is kleiner dan i.
Snellius heeft ontdekt hoe i en r met elkaar samenhangen.
Als je van i en van r de sinus neemt en daarna de sinussen deelt, komt er een constant getal uit.
Hij heeft dit constante getal de brekingsindex genoemd.
Het symbool is n.
n lucht,glas betekent: de brekingsindex voor de overgang van lucht naar glas
Snellius
sin i
sin r
De brekingsindex hangt van de stoffen af en van de kleur van het licht.
Zie BINAS, tabel 18.
formule:
n stof 1, stof 2 
lucht
Bij een suikeroplossing hangt de brekingsindex af van de concentratie. Een refractometer werkt met deze
eigenschap. (Refractie = breking)
water
b. Breking van de normaal af.
Een lichtstraal die uit het water komt zal van de normaal af gebroken worden.
Dus: r is groter dan i.
Geef zelf i en r in de figuur aan.
De brekingsindex is de omgekeerde waarde als die van lucht naar water.
1
formule: nwater ,lucht 
nlucht, water
lucht
water
n lucht,water = 1,33 (BINAS ) dus nwater, lucht= 0,75
8
c . Grenshoek (g).
Een lichtstraal gaat van een dichte stof naar een minder dichte stof.
Bijvoorbeeld van water naar lucht. De lichtstraal breekt van de normaal af.
Nu kan het gebeuren dat de invalshoek zo groot is dat er geen breking plaatsvindt.
Al het invallende licht wordt teruggekaatst!
Dit noemen we totale terugkaatsing. (zie figuur rechts)
De invalshoek waarbij dit nog net niet gebeurt noemen we de grenshoek (g).
Het licht treedt uit het water en loopt langs het oppervlak.
Als de invalshoek gelijk is aan de grenshoek, zal de brekingshoek 90° zijn.
definitie: de grenshoek is de invalshoek die voor een brekingshoek van 90° zorgt.
lucht
water
lucht
water
Uit de grenshoek is ook de brekingsindex te berekenen:
sin i
sin r
i  g dan r  90 
n water ,lucht 
maar sin 90   1
dus
n water ,lucht  sin g
9
3.4 Stralengang in een refractometer
Een refractometer meet de brekingsindex van een vloeistof.
Hiernaast zie je hoe een refractometer werkt.
De vloeistof zit tussen twee glazen blokken.
Je ziet een lichtstraal door het glas en de vloeistof gaan.
Bij overgang naar een minder dichte stof vindt breking van de normaal af plaats.
Bij een te grote hoek van inval krijg je totale terugkaatsing.
Het oog ziet daar een donker vlak.
Hieronder zie je de schaalverdeling in een refractometer.
glas
vloeistof
glas
donker
licht
oog
10
oefensommen hoofdstuk 3
3.3.1
Een lichtstraal wordt gebroken bij de overgang van lucht naar plastic.
De invalshoek bedraagt 58 °
De brekingshoek bedraagt 36 °
Bereken de brekingsindex, nl,p
3.3.2
Een gele lichtstraal komt gaat van lucht naar water.
Zoek de bijbehorende brekingsindex op.
De invalshoek is 76°.
Bereken de brekingshoek.
3.3.3
Een gele lichtstraal komt vanuit het water in lucht.
Bereken nw,l
De brekingshoek is 67°.
Bereken de invalshoek.
3.3.4
ijs
Een lichtstraal breekt als hij van lucht naar ijs gaat.
Bepaal door opmeten i en r. (zie figuur rechts)
Bereken nlucht,ijs
11
3.3.5
Een gele lichtstraal valt op een glazen blok.
a. Bepaal de invalshoek.
b. Het blok is van gewoon glas. Bereken de brekingshoek.
c. Het blok is van zeer zwaar flintglas. Bereken de brekingshoek.
d. Teken voor het geval van vraag c. de stralengang.
glas
3.3.6
water
Zoek de grenshoek van water op.
Maak in een tekening duidelijk wat wordt
bedoeld met de grenshoek van water.
3.3.7
Teken het verdere verloop van de (gele) lichtstraal hieronder.
water
12
3.3.8
Hieronder zie je een gele lichtstraal die een blok van plexiglas binnenkomt.
a. Meet de hoek van inval
b. Zoek de brekingsindex op en bereken de brekingshoek
c. Teken de verdere gang van de lichtstraal
13
Hiernaast zie je een prisma .
De grenshoek bedraagt 45,0 °
a. Bereken de brekingsindex
b. Leg uit waarom de lichtstraal bij I rechtdoor gaat.
c. Meet bij II de invalshoek op.
d. Teken, na rekenen, de stralengang
3.3.9
I
II
14
3.3.10
Van een glazen prisma met hoeken van 45, 90 en 45 graden geldt: n l,g=1,50
Teken in de figuur hieronder de stralengang
15