PowerPoint-presentatie

The art of slaying dragons
There once lived a man
who learned how to slay dragons
and who gave all he possessed
to mastering the art
After three years
he was fully prepared but
alas, he found no opportunity
to practise his skills.
Dschuang Dsi
As a result he began
to teach how to slay dragons
René Thom
ASO - derde graad
Leerplannen wiskunde
 Kader
 Opties leerplannen
 Vrije ruimte
Kader van verandering





Overheid
VVKSO
Overladenheid
Andere voorbereiding tweede graad
ICT verplicht
Overheid
 Opleggen van
eindtermen
(goedgekeurd in Vlaamse raad)
en specifieke eindtermen
(al goedgekeurd in Vlaamse onderwijsraad)
 Invoering derde graad:
1 september 2004
VVKSO
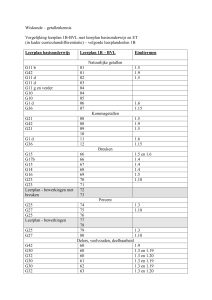
 lessentabel derde graad
wiskunde
wiskunde Compl. Compl.
basisvorming fundameneel
5
6
EC-MT
3
0 +2 0 +3
EC-WI
6
2
2 +1
GR-LA
3
1 +1 1 +2
GR-WE
4
1
1 +1
GR-WI
6
2
2 +1
LA-MT
3
0 +2 0 + 3
LA-WE
4
1
1 +1
LA-WI
6
2
2 +1
HU WE
3
1 +3 1 +3
MT-WE
4
0 +1 0 +2
MT-WI
6
1 +1 1 +2
WE-SP
4
1
1 +1
WE-WI
6
2 +1 2 +2
in 6
Est. -1
Est. -1
Est. -1
Est. -1
Est. -1
Est. -1
Est. -1
Est. -1
Est. -1
Est. -1
Est. -1
Est. -1
in 5 & 6 in 5 & 6
We. -1
MT -1
We. -1
We. -1
MT -1
We. -2
MT -1
MT -1
MT -1
We. -1
VVKSO
 lessentabel derde graad
zoals voorheen 3 – 4 – 6
 complementaire lestijden



8 lestijden blijft een mogelijke “vrije keuze”
Vorming van deze leerlingen blijft belangrijk,
dus ruimer opentrekken naar “brede vorming”!
Ondersteuning LPC kán, vanuit respect voor
vrije ruimte school / leraar (/ leerling?)
visie gs vrije ruimte (vakkenrakend, ….)
ASO - derde graad
Leerplannen wiskunde
 Kader
 Opties leerplannen
 Vrije ruimte
Leefwereld
Werkelijkheidsgebied
Probleem
Model
Analyseren
Mathematiseren
?
Berekenen
Controleren
Interpreteren
Oplossing
Verantwoorden
Ordenen
Creëren
Behandelingstechniek
Behandelingstechnologie
Wiskunde
theorie
Leerplannen ASO
 Leerplan a
……-wiskunde
 Leerplan b
……-wetenschappen
 Leerplan c
Economie-moderne talen
Grieks-Latijn
Humane wetenschappen
Latijn-moderne talen
Leerplannen ASO
LEERPLAN C
1 Vaardigheden en attitudes
2 Verplichte deel
ca. 105
Functieleer
Afgeleiden
Integralen
Exp. & log.
Goniom.
Statistiek
83
25
15
15
15
3 Keuzeonderwerpen
20
ca. 45
Leerplannen ASO
LEERPLAN C
3 Keuzeonderwerpen
ca. 45
Matrices en stelsels
15
Financiële algebra
Ruimtemeetkunde
Lin. regressie en correlatie
Betrouwbaarheidsinterv.
Toetsen van hypothesen
Telproblemen
Kansrekenen
Mathematiseren
Eigen keuze
max.
25
15
15
10
7
10
15
15
15
Leerplannen ASO
LEERPLAN B
1 Vaardigheden en attitudes
2 Verplichte deel
ca. 146
Functieleer
Afgeleiden
Integralen
Exp. & log.
Goniom.
Rationale
Statistiek
126
25
15
25
30
18
3 Keuzeonderwerpen
20
ca. 54
Leerplannen ASO
LEERPLAN B
3 Keuzeonderwerpen
ca. 54
Complexe getallen
12
Matrices en stelsels
Financiële algebra
Ruimtemeetkunde
Lin. regressie en correlatie
Betrouwbaarheidsintervallen
Toetsen van hypothesen
Telproblemen
Kansrekenen
Rijen en iteratie
Mathematiseren
Eigen keuze
max.
15
25
15
15
10
8
10
15
20
20
20
Leerplannen ASO
LEERPLAN A
De decretale specifieke eindtermen wiskunde
hebben betrekking op kennis, inzichten,
vaardigheden en attitudes waarmee leerlingen:
 verbanden leggen tussen wiskunde en
praktische toepassingen uit het dagelijkse leven
en zo relaties leggen met problemen uit
maatschappij, wetenschap en techniek;
 verbanden leggen binnen de wiskunde en
daarmee hun wiskundig kader meer
systematisch ordenen;
 een wiskundig denken en redeneren ontwikkelen,
d.w.z. een wiskundig eigen wijze van:
Leerplannen ASO
LEERPLAN A
… een wiskundig eigen wijze van



• bevragen, onderzoeken en formuleren van
vermoedens
• modelleren en structureren
• argumenteren en bewijzen;
gesloten en open problemen wiskundig kunnen
stellen en analyseren, en oplossingen
argumenteren en bespreken;
communiceren over wiskundig beschreven
situaties, met inbegrip van het vlotte gebruik
van meer specifieke wiskundetaal;
kritisch reflecteren op denken en handelen.
Leerplannen ASO
LEERPLAN A
Er moet aandacht besteed worden aan:






een efficiënte conceptvorming;
een adequaat en meer geformaliseerd taalgebruik;
de ontwikkeling van meer specifieke wiskundige
methoden en werkwijzen;
een accuraat aanwenden van heuristiek en
probleemoplossende vaardigheden;
een zinvol gebruik van ICT;
een meer systematische ordening van de
domeinspecifieke kennis.
Vrije ruimte
Verdieping
Uitbreiding
Basis
Kern
Leerplannen ASO
LEERPLAN A
 Basis: Kern-Verdieping

Conceptvorming/begripsvorming
• Betekenisgeving, context

Techniciteit (berekeningen)
• Beperken
• ICT

Fundamenten
• Kern of verdieping

Toepassen
 Uitbreiding/keuze
 Verband met vrije ruimte
Leerplannen ASO
LEERPLAN A
Analyse
Discrete wiskunde
Algebra
Meetkunde
Statistiek
Onderzoeksprojecten
Verdieping
Keuze
40 %
6%
10 %
10 %
10 %
4%
10 %
10 %
leerplan a - concreet
 Analyse

Algemene doelstellingen
problemen oplossen, manueel rekenen, ICT

Precalculus
• Veeltermfun, rationale, irrationale fun
V: + k, . k; samengestelde functies
U: rekenen met rat v.; irration vergel.; verschuiven
assenstelsel
• Exponentiële en logaritmische functies
U: log. schaal
• Goniometrische functies
V: Cyclometrische
leerplan a - concreet
 Analyse

Afgeleiden & Integralen
• Concept afgeleide, verloop,
extremumproblemen, asymptotisch gedrag
• Concept integraal, integratiemethodes
Splitsen, substitutie, partiële integratie
V: formelere definities, middelwaardestellingen,
oneigenlijke integraal
U: de l’Hospital, partieelbreuken, booglengte,
K: Differentiaalvergelijkingen
K: Convergentie reeks
K: Numerieke methoden
leerplan a - concreet
 Discrete wiskunde

Rijen en dynamische processen
• Convergentie
– Begrip oneindig
• Recursieve rijen
• Discrete veranderingsprocessen
K: Iteratie

Telproblemen
leerplan a - concreet
 Algebra

Complexe getallen
Begrip, rekenen, goniom. vorm, …
U: veeltermverg.nde graad, meetk. interpr.bewerkingen
K: Fractalen

Matrices
Begrip, berekeningen
Rijherleiden, stelsels
V: Inverse, stelsels één parameter
U: Determinant, eigenwaarden
K: Lineaire programmering
K: Financiële algebra
K: Getaltheorie
leerplan a - concreet
 Meetkunde

Ruimtemeetkunde
•
•
•
•
Vectorruimte (dim drie, coördin)
Rechte, vlak
Loodrechte stand, afstanden
Toepassen in meetkundige problemen
synthetisch en analytisch
vlak en ruimte
U: Bol, Krommen en oppervlakken, Transformaties
K: Analytische meetkunde
leerplan a - concreet
 Statistiek en kansrekenen

Statistiek
• Statistische gegevens interpreteren
– Steekproeftrekken
• Normale verdeling, standaardnormale verd.
• Betrouwbaarheid
K: Lineaire regressie en correlatie
K: Toetsen van hypothesen

Kansrekenen
• Begrip, voorwaardelijke kans
• Kansen bij normaalverdeelde gegevens
• Binomiale verdeling
leerplan a - concreet
Vanuit de eindtermen ook nog
 Wiskunde en cultuur
 Onderzoekscompetenties
Suggesties vanuit de uitbreiding en de
keuzeonderwerpen
ASO - derde graad
Leerplannen wiskunde
 Kader
 Opties leerplannen
 Vrije ruimte
Vrije ruimte
Principes

Vakoverschrijdende aanpak
• ‘vak’betrokken - vakkenbetrokken
• Vakkenrakend
• Niveau algemene vorming

Projectmatige aanpak
• Niet-exhaustief, deelaspect uitvergroot

Zelfsturend leren
• Begeleid zelfstandig leren

Uitdiepend leren
Hoe hiermee omgaan?
 Revolutie?
 Koppeling van vrije ruimte



aan zinvol “leren”,
aan verwerven van inhouden,
vaardigheden, attitudes, opvattingen, …
een bijzondere mogelijkheid hiertoe is
o.m. het koppelen van vrije ruimte aan
poolvakken (vormingtrekkende vakken)
Cf. een aantal keuzeonderwerpen geven aanleiding
tot ‘vrije ruimte’
Hoe hiermee omgaan?
 Wij hebben wat gevraagd wordt


Zelfsturend leren, projectmatige aanpak,
vakoverschrijdende aanpak past bij een
vernieuwde wiskundeaanpak
Vandaaruit constructief deelnemen aan de
begeleidingsgroep – schoolwerkgroep
 Werkgroep wiskunde op niveau
scholengemeenschap, diocees?


Opzoekwerk
Uitwisseling
Vrije ruimte en wiskunde
 Twee denkpistes


Aanzet vanuit wiskundeleraar
Aanzet vanuit vakoverschrijdend
samenwerken
vanuit wiskundeopdrachten
•
•
•
•
•
•
•
•
Coderen (cf. getaltheorie)
Dataverwerking (cf. statistiek, correlatie, …)
Planetenbanen (cf. kegelsneden)
Lenen en beleggen (cf. financiële algebra)
Groei
Benaderen
Testen en voorspellen
Simulatie
•…
vanuit wiskundeopdrachten
cf. zebraboekjes:
Kattenaids en statistiek
Perspectief, hoe moet je dat zien
Schatten, hoe doe je dat
De gulden snede
Poisson, de Pruisen en de lotto
Pi
De laatste stelling van Fermat
Verkiezingen, een web van
paradoxen
Veelzijdigheid van bollen
Fractals
Schuiven met auto's, munten en
bollen
Spelen met gehelen
Wiskunde in de Islam
Grafen in de praktijk
De juiste toon
Chaos en orde
vanuit vakoverschrijdende opdrachten
Architectuur en wiskunde
Atletiekrecords
Beleggen met wiskunde
Binaire coderingen
Blikken
Bouwen met regelmatige
figuren
Cartografie
Chaostheorie
Conditie en uithoudingsvermogen
DNA-test
Ecosystemen
Egyptische breuken
Elfstedentocht en zonneactiviteit
Escher
Fibonacci en het getal phi
Fractalen
Fruitautomaat
Geometrie in de gouden
eeuw
Gewicht en evenwicht
Global Positioning System
Girlpower
Groei wereldbevolking
Groeimodellen
Het handelsreizigersprobleem
Huren of kopen?
Islamitische wiskunde
Kiezen en wiskunde
Kunst en wiskunde
Kortste wegennet
Leesbaarheid
Lengtegroei en welvaart
Literatuur en wiskunde
Luiers wassen of wegwerpen?
Pascal nader bekeken
Perfecte getallen
Plaats ijscokar
Polynomen en patronen
Randomized response
Roken, hoe lang nog?
Roulette to win or not to
win
Sportland
Toren van Hanoi
Verpakkingen
Vlak- en ruimtevullingen
Warmteverlies
Wiskundige spellen
vanuit vakoverschrijdende opdrachten
Vaardigheden
Was Oranje wel zo goed?
Energie in huis
IJscokar
Functies en grafieken
Overgewicht
De C-14 methode
Huidoppervlakte
De geschiedenis van de
formule
De formule van Cardano
Rijden maar
Discrete analyse
Bevolkingsgroei in Nederland
De ontwikkeling van
wereldrecords
Hypotheek gratis door
inflatie
Handelsreizigersprobleem
Meetkunde
De Platonische lichamen
Koffiebekertje
Caleidocyclus
Obelisken in Egypte
Amsterdam die mooie stad
Wiskunde en kunst
Perspectief
Volvo Ocean Race
Differentiaal- en
integraalrekening
Files
Windenergie
De kogelbaan
Continue dynamische
modellen
Modelleren in Excel
Groeimodellen
Goniometrische functies
Exoplaneten
Krommen op de kermis
Rozen, limaçons en andere
krommen
Combinatoriek en
kansrekening
Verspreiding van de euro
Verkiezingen
De toekomst van het weer
Gooien maar
Op tijd?
Wiskunde B2
Enigma
Perfecte getallen
Wonderrecept
De oogbalstelling
Vrije ruimte – i-handboek
 Suggesties wiskunde





Geschiedenis en wiskunde
Codering en informatieverwerking
Wiskunde en kunst
Mathematiseren en het oplossen van
problemen
Bijkomende suggesties
Vrije ruimte
 Praktische suggesties



Niet alles in ‘projecten’
‘Behoud’ bestaande projecten
Geleidelijke overgang
• Leerfase leerkrachten
• Behoud lestijden seminarie + ‘contract/engagement’
• Infrastructuur: mediatheek / ICT / OLC

Vrije ruimte namiddag
• Keuze bij leerlingen vanuit aanbod
• Verschillende coachen aanwezig; uitwisselbaar

Projectweken, rest normaal lesrooster (bijv. 22 of 23

In 5de leerjaar voorbereiden via miniopdrachten
weken); compensaties?
• Leerfase leerlingen zelfstandig werken