Een karretje rijdt op een paar horizontale metalen

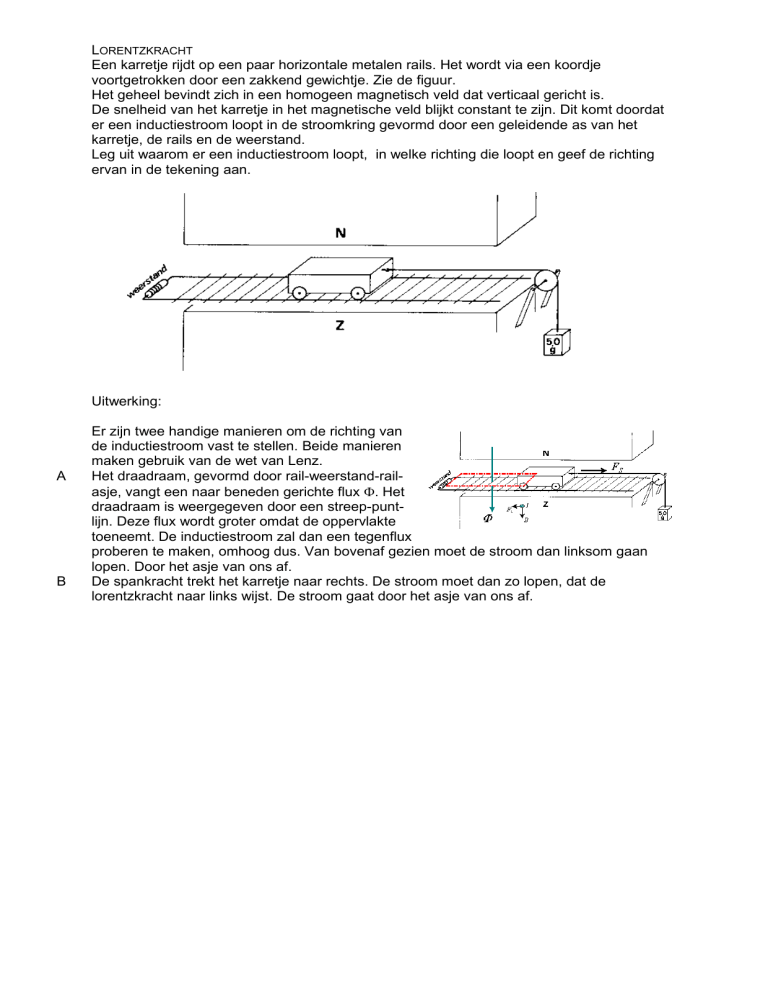
LORENTZKRACHT
Een karretje rijdt op een paar horizontale metalen rails. Het wordt via een koordje
voortgetrokken door een zakkend gewichtje. Zie de figuur.
Het geheel bevindt zich in een homogeen magnetisch veld dat verticaal gericht is.
De snelheid van het karretje in het magnetische veld blijkt constant te zijn. Dit komt doordat
er een inductiestroom loopt in de stroomkring gevormd door een geleidende as van het
karretje, de rails en de weerstand.
Leg uit waarom er een inductiestroom loopt, in welke richting die loopt en geef de richting
ervan in de tekening aan.
Uitwerking:
A
B
Er zijn twee handige manieren om de richting van
de inductiestroom vast te stellen. Beide manieren
maken gebruik van de wet van Lenz.
Het draadraam, gevormd door rail-weerstand-railasje, vangt een naar beneden gerichte flux . Het
draadraam is weergegeven door een streep-puntlijn. Deze flux wordt groter omdat de oppervlakte
toeneemt. De inductiestroom zal dan een tegenflux
proberen te maken, omhoog dus. Van bovenaf gezien moet de stroom dan linksom gaan
lopen. Door het asje van ons af.
De spankracht trekt het karretje naar rechts. De stroom moet dan zo lopen, dat de
lorentzkracht naar links wijst. De stroom gaat door het asje van ons af.
VERVOLG:
Een karretje rijdt op een paar horizontale rails. Het wordt via een koordje voortgetrokken
door een zakkend gewichtje.
De massa van het gewichtje is 5,0 g. Er treedt nergens wrijving op.
De afstand tussen de rails is 48 mm. Zie figuur.
Het geheel bevindt zich in een homogeen magnetisch veld dat verticaal gericht is.
De sterkte ervan is 0,50 T. Slechts één van de assen van het karretje vormt een geleidende
verbinding tussen de rails. De snelheid van het karretje in het magnetische veld blijkt
constant te zijn. Dit komt doordat er een inductiestroom loopt in de stroomkring gevormd
door de geleidende as van het karretje, de rails en een weerstand.
Bereken de grootte van de inductiestroom.
U = I × R levert meteen 3 onbekenden. Dat lijkt niet de weg.
In de inleiding staat dat het karretje met constante snelheid rijdt. Jij moet dan onmiddellijk
concluderen: F = 0 en dus FL = Fz.
De volgende stap is: BIL = mg, waarvan alles bekend is op de stroom na. Nu kunnen we
invullen en rekenen: 0,50 × I × 0,048 = 5,0103 × 9.81  I = 2,0 A
SPANNEND
Je ziet hieronder een grafiek van de door een spoel ontvangen flux  als functie van de tijd.
Bepaal de inductiespanning als functie van de tijd en teken de grafiek ervan.
Uitwerking:
De inductiespanning is evenredig met de fluxverandering per seconde en dus met de
steilheid van de lijnen in de grafiek. Er komen dus twee verschillende waarden, tegengesteld
van teken.
In de eerste 0,6 s:
U ind  
Dan:

3 0
 
 5 V
t
0,6  0
U ind  

 1 3
 
 20 V
t
0,8  0,6
TRANSFORMATOR
Leg uit waarom de transformator besproken wordt in een hoofdstuk over inductie.
A
B
VALLENDE MAGNEET
Een 2 cm lange staafmagneet valt door een 30 cm lange spoel. De noordpool zit aan de
onderkant van die staaf magneet. De bovenkant van de spoel noemen we A, het midden
van de spoel noemen we B en de onderkant noemen we C. Tussen de uiteinden van de
spoel is een lichtgevende diode aangesloten, een zgn. LED.
De doorlaatrichting van de LED is van boven naar beneden. Bij het passeren van A zien we
die kort oplichten.
Schets de spoel met LED. Zet de punten A, B en C erbij en maak duidelijk hoe de spoel
gewikkeld is.
Parallel aan de LED sluiten we een voltmeter aan, zodat deze de spanning tussen de
uiteinden van de spoel meet. We laten opnieuw het staafmagneetje met de noordpool naar
onder er door vallen.
Leg uit bij het passeren van welk van de punten A, B en C de gemeten spanning het hoogst
zal zijn.
HALOGEEN SPOTBOOG
Het is de dag van de reclames in de bus. Daar zit een reclame bij van een halogeen
verlichting, zoals hieronder is afgebeeld. Je ziet 4 halogeenlampen (12V; 20 W) aangesloten
op een transformator. Die zit in de zwarte cilinder in het midden van de lamp. Zie foto.
A
B
C
A
De transformator moet aangesloten worden op de netspanning van 230 V; 50 Hz.
De vier halogeenlampen branden zoals bedoeld.
Ze zijn bevestigd tussen twee metalen bogen zoals afgebeeld in de tekening. De bogen zijn
geleidend verbonden met twee metalen rechte staven, die beide in het midden contact
maken met een uiteinde van de secundaire spoel van de transformator.
Bereken wat de verhouding moet zijn tussen het primair en secundair aantal windingen.
Bereken ook de effectieve en de maximale
stroomsterkte in de rechte staven.
Teken de grafiek van het door de
transformator geleverde vermogen als functie
van de tijd. Licht je grafiek toe.
Uitwerking:
De lampen zijn parallel geschakeld. Ze branden dus allemaal op dezelfde spanning: 12 V.
De primaire spanning is 230 V, de secundaire 12 V.
Np
Ns
B
C

Vp
Vs

230
 19
12
Voor iedere lamp geldt:
P = I × U  20 = I × 12  I = 1,67 A.
Bekijk de schakeling een goed. Bij de
transformator splitst de secundaire stroom zich in
twee takken die elk twee lampen van stroom
voorzien.
Dus Ieff, staaf = 3,4 A en Imax,staaf = Ieff, staaf  2 = 4,7A.
Het door de transformator effectief geleverde vermogen is 4 × 20 = 80 W.
Bedenk dus dat vanwege het middelen, het topvermogen 160 W is.
Door de frequentie van 50 Hz wisselt de stroom 50 maal per seconde.
Maar de warmteontwikkeling is onafhankelijk van de stroomrichting en wisselt dus 100 maal
per s.
De grafiek is een periodieke functie met een periode van 0,010 s.
ENERGIETRANSPORT
De generator bij de elektriciteitscentrale levert 1,6 GW bij een spanning van 2700 V.
Bij de centrale wordt de spanning omhoog getransformeerd naar 380 kV om dan via een
hoogspanningskabel te worden getransporteerd naar de afnemers. Bij de afnemers staan
weer transformatoren die de spanning terugbrengen naar uiteindelijk 230 V.
Je mag de transformatoren als ideaal beschouwen.
A
Bereken de wikkelverhouding in de transformator bij de centrale.
Onderweg treden door warmte-ontwikkeling verliezen op. De hoogspanning na transport
blijkt een waarde te hebben van 370 kV.
B
Bereken de elektrische weerstand van de hoogspanningskabel.
Uitwerking:
De inleiding verwerken we eerst tot een tekening van de situatie.
Up
A
B
Us

np
ns

np
ns

2700
380  10 3
Je mag hier van maken 1:141.
De weerstand bereken je met U = IR.
De spanning U over de weerstand is
380  370 = 10 kV.
We moeten de stroomsterkte I nog
berekenen.
De stroomsterkte volgt uit het geleverde vermogen.
P = IU  1,6109 = I × 380103  I = 4211 A.
U = IR  10103 = 4211 × R  R = 2,4 
Een andere taktiek is dat je uit het spanningsverlies concludeert dat er 10/380e deel van het
vermogen verloren gaat in de weerstand, dus 10/380 × 1,6109 = 42106 W.
Dat is de warmte-ontwikkeling in de draad. P = U²/R  42106 = (10103)² / R 
R = 2,4 .
INDUCTIESPANNING
In een spoel wordt een flux  opgewekt, die voldoet aan (t) = 0,10 × sin (2 × 50t).
De (t)- grafiek is afgebeeld.
Midden in die spoel brengt men een klein
meetspoeltje van 80 windingen. De assen
van beide spoelen vallen samen.
A
Schets in de gegeven fluxgrafiek de gemeten inductiespanning als functie van de tijd
Niet alle gegevens van de spoel en het meetspoeltje zijn bekend. Daarom kun je niet
uitrekenen wat de maximale waarde van de gemeten inductiespanning is.
B
Leid af wat de theoretisch maximale waarde van de gemeten inductiespanning is en
welke gegevens je nog nodig hebt om de feitelijke maximale waarde te kunnen
berekenen.
A
B
Uitwerking:
De inductiespanning is evenredig met de afgeleide van de omsloten flux.
Waar de flux een uiterste waarde bereikt en de
afgeleide dus nul is, is de inductiespanning dat
ook. Waar de flux het sterkst verandert, is de
inductiespanning maximaal. Daalt de flux, dan is
de inductiespanning positief.
Omdat de eenheid weber en volt verschillend
zijn, kun je als schaal voor de spanning zelf een
keuze maken.
Aan de formule zie je dat de frequentie 50 Hz is
en dus T = 0,020 s.
U ind ,max  

t
 
raaklijn
 0,1  0,1
 30 V
0,02 / 3
per winding, dus maximaal 2,4 kV in de
veronderstelling dat de kleine spoel alle veldlijnen, gemaakt door de grote spoel omvat. Daar
de diameter van de kleine spoel kleiner is dan de binnendiameter van de grote, zal de
feitelijke kleiner zijn. Je moet dus weten welke fractie van de totale flux gevangen wordt door
de kleine spoel.
Ook mogelijk: Uind = ’ = 0,10 × 2 × 50 × cos (2 × 50t) 
Uind, max = 0,10 × 2 × 50 = 31 V per winding. De windingen zijn seriegeschakeld, dus Uind,max =
80 × 31 = 2,5 kV
A
B
DYNAMO
Bij een dynamo wordt een sinusvormige wisselspanning opgewekt bij een frequentie van 50
Hz en grafisch weergegeven.
Zie nevenstaande grafiek.
Bepaal de effectieve spanning van
de dynamo onder die
omstandigheden.
We verlagen het toerental van de
rotor zodat de afgegeven frequentie
40 Hz bedraagt.
Teken in de reeds getekende grafiek
die bij de 50 Hz hoorde, de grafiek
zoals je die nu verwacht. Licht je
grafiek toe.
Uitwerking:
Denk niet alleen aan de nieuwe trillingstijd, 0,025 s, maar ook aan de kleinere Utop.
Er staat 'teken' en dat vereist een grote nauwkeurigheid.
Bij Ueff = 220 V hoort een Utop = 220 × 2 = 311 V. Nu bij 40 Hz is die top slechts
40
U top 
 311  249 V  U eff  249  12 2  176 V
50
A
B
VALLENDE MAGNEET
Een 2 cm lange staafmagneet valt door een 30 cm lange spoel. De noordpool zit aan de
onderkant van die staaf magneet. De bovenkant van de spoel noemen we A, het midden
van de spoel noemen we B en de onderkant noemen we C. Tussen de uiteinden van de
spoel is een lichtgevende diode aangesloten, een zgn. LED.
De doorlaatrichting van de LED is van boven naar beneden. Bij het passeren van A zien we
die kort oplichten.
Schets de spoel met LED. Zet de punten A, B en C erbij en maak duidelijk hoe de spoel
gewikkeld is.
Parallel aan de LED sluiten we een voltmeter aan, zodat deze de spanning tussen de
uiteinden van de spoel meet. We laten opnieuw het staafmagneetje met de noordpool naar
onder er door vallen.
Leg uit bij het passeren van welk van de punten A, B en C de gemeten spanning het hoogst
zal zijn.
GLOEILAMP
Op een gloeilamp staat 230 V. De gloeilamp wordt aangesloten op het net, waardoor er een
stroom I gaat lopen. Voor de stroom geldt I(t) = 0,25 × cos (2 × 50t)
Bereken het elektrisch vermogen waarvoor deze lamp is bedoeld.
KETTING
Er bestaat een idee om van de ketting van je fiets
een dynamo te maken. In iedere schakel van je
ketting zou dan een magneetje worden geplaatst.
Naast de ketting komen dan spoelen.
Als je gaat fietsen, blijven de spoelen op hun
plaats, maar verschuiven de schakels en wordt er
een spanning opgewekt in de spoelen.
Op het tijdstip t = 0 is de situatie zoals in
nevenstaande figuur 1 is weergegeven.
De magneten bewegen naar boven in die figuur.
Na een tijdje T zijn de magneten een plaats
opgeschoven en ziet de situatie er weer net zo uit.
A
B
C
A
Geef door middel van veldlijnen in figuur 1 op het antwoordblad het magneetveld weer van
uitsluitend de magneet naast spoel CD.
Maar er zijn meer magneten. De flux voor
spoel CD als functie van de tijd is
geschetst in figuur 2.
Schets op het antwoordblad met
dezelfde tijdas de bijbehorende
inductiespanning in spoel CD als functie
van de tijd. De interessante plaatsen zijn
‘verlengd’.
In figuur 2 is een tijdstip S vlak na t = 0 aangegeven met een sterretje.
Leid af in welke richting de inductiestroom op dat moment door de spoel gaat. Van C naar D
of van D naar C.
Alternatieve vragen:
Geef door middel van veldlijnen in figuur 1 het magneetveld weer van uitsluitend de
magneet naast spoel CD en in figuur 2 het magneetveld van de aaneenschakeling van
magneten, die je kunt nummeren 1, 2, 3, enz......
Gebruik daarbij per noordpool 5 veldlijnen.
B
Schets een grafiek van de flux in spoel CD als functie van de tijd t voor 0 tot 2T
C
Schets met een andere kleur de grafiek van de flux in spoel CD als functie van de tijd als bij
dezelfde fietssnelheid de magneten met een oneven nummer worden verwijderd.
A
B
ENERGIETRANSPORT
Een generator wekt maximaal 500 MW elektrische energie op bij een spanning van 2700 V.
Dit wordt via hoogspanningskabels naar de afnemers vervoerd. Het omhoog en omlaag
transformeren gebeurt in ideale transformatoren. De transformator bij de generator heeft een
wikkelverhouding 1:140. Zie figuur.
Bereken de secundaire spanning en
stroomsterkte bij deze transformator.
De hoogspanningskabels hebben
een weerstand waardoor elektrische
energie verloren gaat.
Bereken de primaire spanning van
de transformator bij de afnemers als
het maximaal vermogen wordt gebruikt en 4% van de elektrische energie verloren gaat aan
warmte.
MAGNETISME
Aan een spaak van een fietswiel is een magneetje bevestigd. Als het
wiel ronddraait, passeert het magneetje een spoel die op de voorvork is
bevestigd. Zie de afgedrukte foto hiernaast. In de tekening eronder is dit
schematisch weergegeven.
A
B
C
D
Als het magneetje de spoel passeert, wordt een inductiespanning
opgewekt. Terwijl een fietser met constante snelheid rijdt, wordt deze
inductiespanning als functie van de tijd gemeten. Het
resultaat is weergegeven in de grafiek.
De diameter van het fietswiel is 71 cm.
Bepaal de snelheid van de fletser.
De fletser gaat sneller
fietsen. Opnieuw wordt
een (Uind,f)-diagram
gemaakt. Dit nieuwe
diagram heeft een
aantal verschillen met
de weergegeven
grafiek.
Noem deze verschillen
en leg van ieder
verschil uit waardoor
het ontstaat.
Of je als eerste een
neerwaartse piek te
zien krijgt, zoals in de gegeven grafiek, of een opwaartse, hangt af van de aansluitingen. In
de schematische tekening verwijdert het magneetje zich van de spoel die zich aan onze kant
van het magneetje bevindt.
Leg uit of in die situatie de boven- of onderkant van de voltmeter positief is t.o.v. de ander
kant.
Het magneetje heeft een massa van 20 g en bevindt zich 7,1 cm van het middelpunt van het
wiel.
Bereken de grootte van de vereiste middelpuntzoekende kracht op het magneetje, als de
fietser een constante snelheid heeft van 18 km/h.
A
Uitwerking:
Uit de grafiek leid je een periode van 0,5 s af. In 0,5 s draait het wiel dus eenmaal rond.
v
B
x 2 r   0,71


 4,46 m / s
t
T
0,50
 v = 4,5 m/s.
Sneller rond, periode kleiner, horizontale schaal kleiner: pieken smaller en volgen elkaar
sneller op.
Vind 
C
D

 t  De fluxverandering vindt in een kortere tijd plaats, dus de inductiespanning is
groter, de pieken dus hoger.
De noordpool maakt veldlijnen in onze richting. De noordpool verwijdert zich van de spoel en
dus neemt de flux door de spoel af. de inductiespanning zal proberen dat tegen te gaan door
juist veldlijnen onze kant uit bij te maken. Daartoe zal in de spoel een inductiestroom willen
ontstaan tegen de wijzers van de klok in, gezien van onze kant. Zou je een weerstand
opnemen i.p.v. de voltmeter dan loopt de stroom daardoor van boven naar beneden. De
bovenkant van de V-meter is dus positief.
Je mag geen conclusies trekken uit het feit dat in de grafiek eerst een dal komt en dan een
piek. Dat staat juist in de inleiding.
18 km/h = 5 m/s aan de rand van de band. De dynamo zit op 7,1 cm, terwijl de straal van de
band 35,5 cm = 5 × 7,1 cm is. De snelheid van het magneetje is dus 1,0 m/s.
Fmpz
mv 2 0,020  1,0 2


 0,28 N
r
0,071
.
Je kunt ook werken met F = m²r.
A
B
C
INDUCTIE EN INFORMATICA
Via een pad, waar auto’s elkaar niet
kunnen passeren, kom je bij de
goederenafgifte van een bedrijf. Daar
zit ook de portier.
De portier hoort dankzij een sensor
wanneer er een (vracht)auto aankomt,
maar hij krijgt geen geluidssignaal
wanneer er een wegrijdt.
In fietsers is hij niet geïnteresseerd. Er wordt een systeem ontwikkeld dat hiervoor kan
zorgen. Het ontwerp staat onder aan de bladzijde.
Als sensoren worden 2 inductielussen in het pad gebruikt.
Lus P bij de poort aan het begin van het pad en lus H halverwege het pad.
Iedere inductielus bestaat uit bestaat uit twee spoelen.
Spoel 1, aangesloten op een voeding, en een spoel 2, die wordt aangesloten op een
sensoringang. Zie tekening.
De twee inductielussen liggen zover van elkaar af dat de een na de ander een signaal geeft,
maar nooit tegelijk. Deze lussen geven een signaal af als een ijzeren voorwerp passeert,
dankzij het verschijnsel inductie.
Leg de werking uit van een inductielus. Je kunt hierbij gebruik maken van nevenstaande
tekening.
Het signaal van de lussen gaat naar de sensoringangen A en B.
Leg uit waarom de ontwerper van het systeem comparators in zijn ontwerp wil opnemen.
Leid af of lus P met ingang A verbonden moet worden en lus H met B, of juist andersom.
Uitwerking:
Met de rechterhandregel stel je vast dat je duim en daarmee de veldlijnen omhoog wijzen en
op de plaats van het vraagteken een N moet staan van noordpool.
Als de auto boven de spoelen komt wordt door het ijzerwerk de magnetische inductie B
vergroot. De flux naar boven neemt dus toe. De inductiestroom die daardoor ontstaat, zal dit
proberen tegen te werken en dus veldlijnen naar beneden gaan maken. Maar dan moet
volgens de rechterhand de stroom aan de voorkant van B naar A lopen. Sluit je op de spoel
een weerstand aan tussen A en B, dan loopt daardoor de stroom van A naar B.
Stroom door een weerstand loopt van + naar  A is dus positief t.o.v. B.
Als de auto de spoel nadert, neemt B toe. Als de toename het sterkst is, is de
inductiespanning maximaal. Dat is in ieder
geval niet als de auto midden boven de
spoel is, want dan is de flux maximaal en de
afgeleide ervan juist nul. Maar bij het
‘binnenrijden’ en ‘verlaten’ van de spoel
moet de verandering in flux een keer
maximaal zijn en dus ook de
inductiespanning
VARIAC
Een ideale variac is een ideale
transformator, waarbij men door
middel van een schuifcontact S een
groter of een kleiner aantal secundaire
windingen kan inschakelen. Zie voor
een schematische weergave van een
variac de figuur.
A
B
A
Het aantal primaire windingen
bedraagt 440.
De primaire spoel wordt aangesloten
op
een wisselspanning Vp van 220 V, 50 Hz; de secundaire spanning Vs kan dan worden
gevarieerd van 6,0 V tot 260 V als de schuifweerstand wordt verschoven.
Bereken tussen welke aantallen het aantal secundaire windingen kan worden gevarieerd.
Men stelt de variac op 6,0 V in en sluit op de secundaire spoel nu ook nog een lampje (6,0 V;
0,50 A) aan.
Schets een grafiek van de stroomsterkte in de primaire spoel als functie van de tijd met een
geschikte schaalverdeling.
Uitwerking:
Als er niets bijzonders bij staat heeft men het altijd over de effectieve waarde. Overigens
moet je consequent zijn. Veronderstel je dat 220 V de maximale waarde is van de
wisselspanning, dan moet je dat ook bij 6,0 V veronderstellen.
Up
Us
Up
B


np
ns
np

220 440

 ns  12
6
ns

220 440

 ns  520
260
ns
ns
Transformatorverhouding: U s
Variëren tussen 12 en 520 windingen secundair.
De primaire stroomsterkte moet je eerst uitrekenen.
Energiebehoud: (I × U)p = (I × V)s
220 × Ip = 0,50 × 6,0  Ip = 14 mA. Dat is de effectieve waarde. De topwaarde is 2 maal zo
groot dus 19 mA. Dat moet je wel uitrekenen omdat dat in een grafiek tot uiting komt. 50 Hz
betekent een periode van 1/50 s = 20 ms.
Teken een sinus met een periode van 20 ms en een uitersten van -19 en +19 mA.
EEN SPOEL IN EEN MAGNETISCH VELD
Een spoel is opgehangen aan een veer.
De spoel hangt voor een gedeelte in een homogeen
magnetisch veld. De spoel is opgenomen in een elektrische
schakeling. Zie de figuur.
De spoel KLMN is rechthoekig van vorm en heeft 200
windingen van koperdraad waarvan er twee getekend zijn
in de figuur.
De elektrische schakeling bestaat uit een ideale
spanningsbron van 6,0 V, een schuifweerstand en de
spoel, aangesloten op de in de figuur aangegeven manier.
A
De afstand van de onderkant van de spoel tot de grens van
het magnetische veld wordt y genoemd. Zie de figuur.
Als de spanningsbron nog niet is aangesloten, is y gelijk aan 5,0 cm. MN = 10,0 cm. De
spanningsbron wordt nu aangesloten, zodat de veer verder wordt uitgerekt doordat er een
lorentzkracht werkt. De stroomsterkte in de spoel kan worden veranderd door de schuif van
de schuifweerstand te verplaatsen. Bij een grotere stroomsterkte rekt de veer meer uit.
Leg uit hoe het magnetische veld is gericht.
De spanningsbron en de schuifweerstand met de toevoerdraden tot aan P en Q worden
verwijderd. Men trekt de spoel 4,0 cm uit de evenwichtsstand omlaag en laat die dan los. De
spoel gaat dan harmonisch trillen. Daardoor verandert de door elke winding omvatte
magnetische flux . Het verloop van de flux  door één winding is in de grafiek
weergegeven als functie van de tijd t.
B
Bepaal de maximale waarde van de spanning die tussen P en Q ontstaat.
A
Uitwerking:
De meesten gaan over inductiestroom spreken. Dat is niet verboden, maar zet je op het
verkeerde been. Als je de stroom door de spoel van 200 windingen groter maakt, zal de
lorentzkracht toenemen. Kennelijk wijst die naar beneden. Omdat de stroom op NK naar
rechts loopt, moet het magneetveld wel ‘het papier uit’ wijzen.
Menigeen komt wel tot deze richting, maar via een verkeerde route!
B
Vind = N × ’.
Bepaal dus de afgeleide van de flux, waar de flux het meest verandert. Dat is als de waarde
10103 Wb is. Trek daar een raaklijn. Doen!!!
Mijn raaklijn gaat door (2,25103 Wb; 0 s) en (0 Wb; 0,105 s).
Dus is ’ = 2,25103 / 0,105 = 21 mV en Uind = N × ’ = 200 × 0,021 = 4,3 V
Je mag natuurlijk ook de afgeleide bepalen via de wiskunde. Maar dan wel de goede formule
gebruiken:  = 0,80103 × cos (2 × t/0,24) + 1,0103 Wb.
Een voordeel heb je de afgeleide van 1,0103 is 0 en je moet de maximale waarde van de
sinus hebben en die is 1. Scheelt weer in het rekenen.
A
B
FLUX
Hierbij een grafiek van de flux , zoals die door een spoel wordt opgevangen, als functie van
de tijd t.
Schets de bijbehorende grafiek van de inductiespanning als functie van de tijd.
Zorg dat de tijdas duidelijk is.
De maximale flux in de grafiek is 0,21
Wb. De periode T van de sinus is 4,00
ms.
Bepaal of bereken de
inductiespanning op t = 0,16 s.
UITWERKING:
A
B
Vind    ' .
Dat betekent dus de afgeleide
bepalen en daarvan het
tegengestelde nemen.
De maxima en minima geven dan 0.
Waar de steilheid het sterkst is, is de
afgeleide het grootst. Waar de flux
het sterkst stijgt, krijgen we een
negatieve uiterste voor de
inductiespanning en waar die het
sterkst daalt de positieve uiterste
waarde.
Bedenk dat 4,00 ms betekent: 4,00103 s.
Dan is 0,16 s een tijd van 40 periodes en heeft de inductiespanning juist zijn maximale
waarde, tenminste als het 40,00 periodes zijn. Want als 40 periodes betekent met een marge
van 0,5 periode, dan is iedere waarde mogelijk tussen 0 en ± de uiterste waarde.
 (t) = 0,21 × sin 2ft  Uind = ’(t) = 0,21 ×2f × cos 2ft 
Uind, max = 0,21 × 2 / 0,00400 = 330 V.
De cosinus heeft zijn uiterste waarde en is dus ± 1. In plaats van met de formule werken,
mag je ook een raaklijn tekenen en daar de steilheid van berekenen.
EFFECTIEF
Een weerstand van 8,0  sluit men aan op een voeding met een effectieve wisselspanning
van 6,3 V. De maximale spanning wordt ook wel topspanning genoemd.
Bereken het topvermogen dat de weerstand te verwerken krijgt.
Uitwerking:
Umax = 2 × Ueff = 2 × 6,3 = 8,91 V  Ptop = U²/R = 8,91² / 8,0 = 9,9 W
TRAFO
Een transformator wordt aangesloten op 230 V wisselspanning. De secundaire spanning is
12 V. Het secundaire aantal windingen is 270. Aangesloten wordt een lamp die 5,0 W
opneemt aan vermogen.
Bereken de primaire stroomsterkte.
Uitwerking:
Als de lamp 5,0 W opneemt, moet er ook 5,0 W ingaan. Ervan uitgaande dat de trafo geen
verliezen heeft. Primair geldt dan P = I × V  5,0 = 230 × I  I = 0,022 A
Je kunt natuurlijk ook de secundaire stroom uitrekenen en dan gebruik maken van (IU)p =
(IU)s.
SPEELGOED KINDERWAGEN
In deze opgave zijn de belangrijke onderdelen:
De as met wielen van een kinderwagentje; de as met wielen zijn elektrisch goed
geleidend en maken met de rails een prima elektrisch contact.
Een recht stuk rails, waarover de wielen van de kinderwagen kunnen rijden
Een weerstand die de twee rails aan het uiteinde met elkaar verbindt
Een lange horizontale tafel; de rails liggen daarop
Een katrol, touwtje erover; aan het ene uiteinde de as van het karretje, aan het andere
een gewichtje.
Een homogeen magneetveld, loodrecht op de tafel naar beneden gericht.
De situatie is in boven- en zijaanzicht getekend. Laat je het gewichtje los, gaat de as
versnellen en blijkt er een inductiestroom door het asje te lopen.
A
B
A
B.
Leid af in welke richting de stroom door het asje loopt en welk uiteinde van het asje de
positieve pool is.
Het blijkt dat de versnelling van het asje geleidelijk afneemt. Leg dat uit. Maar schets eerst
een snelheid-tijd-grafiek.
Uitwerking:
Bekijk de oppervlakte tussen weerstand, asje en de twee stukjes rails. Als het asje naar
rechts gaat, zal het aantal veldlijnen en dus de flux naar beneden toenemen. De
inductiestroom zal dan veldlijnen omhoog proberen te maken. De rechterhandregel zegt dan
stroom tegen de wijzers van de klok in, dus door de weerstand van A naar B. Stroom door
een weerstand loopt van hoge naar lage potentiaal, dus A moet de positieve pool zijn en B
de negatieve.
Een andere redenering is deze: De spankracht in het touwtje werkt naar rechts. De
lorentzkracht ten gevolge van de inductiestroom zal naar links wijzen. Van de linkerhand
moet de duim naar links, de veldlijnen in de handpalm prikken, dus de stroom naar boven.
Dus door de weerstand naar beneden, dus de bovenste rail A is positief t.o.v. de onderste
rail
Je moet beredeneren dat de versnelling geleidelijk afneemt.
Door de spankracht krijgt het asje een versnelling naar rechts. De neerwaartse flux neemt
toe. Er ontstaat een inductiestroom en een tegenwerkende
lorentzkracht.
De versnelling zal dus worden:
a = (Fz  FL)/masje + gwicht. Door de versnelling gaat het asje
harder. Daardoor grotere fluxverandering, dus grotere
stroom, dus grotere lorentzkracht dus kleinere resulterende
kracht en versnelling. Als het asje de kans krijgt zal de
resulterende kracht nul worden en het asje met constante snelheid verder gaan.
INDUCTIESTROMEN.
Om een weekijzeren U-kern worden twee spoelen van elk 375 windingen geplaatst. Boven
op deze U-kern zijn twee stukken weekijzer bevestigd, zodanig dat er tussen deze twee
stukken een smalle luchtspleet is. Zie de linker figuur. In de rechter figuur is een doorsnede
getekend van de ijzeren kern en de luchtspleet. In deze figuur is een aantal magnetische
veldlijnen getekend. Het magnetisch veld wordt opgewekt door de twee spoelen in serie te
schakelen en aan te sluiten op een gelijkspanningsbron.
A
Voltooi in de rechterfiguur de schakeling waarin deze twee spoelen zijn opgenomen.
Geef in deze schakeling de richting van de elektrische stroom aan.
Voor de sterkte van het magnetische veld B in de luchtspleet van de afgebeelde magneet
geldt bij benadering:
B  0,27 
0  N  I
d
hierin is:
0 de permeabiliteit van vacuum,
N het aantal windingen om de ijzeren kern,
I de stroomsterkte,
d de breedte van de luchtspleet.
B
Bereken de magnetische inductie B in de luchtspleet van de hierboven afgebeelde
magneet als I = 5.0 A en d = 7.0103 m.
Een katrol is voor de helft in de luchtspleet geplaatst. Deze katrol is gemaakt van perspex,
waarin een viertal gesloten lussen van koperdraad zijn aangebracht. Een tweede katrol
bevindt zich verticaal boven de eerste. Zie de linkerfiguur. Over deze katrollen loopt een
touw. Aan dit touw wordt een blokje gevestigd. Als men dit blokje vanuit zijn hoogste positie
loslaat komt het in beweging. De katrollen ondervinden geen wrijving bij het draaien. Het
touw slipt niet tijdens de beweging. Als er geen stroom door de spoelen loopt, is de
beweging van het blokje eenparig versneld. Als er wel een stroom door de spoelen loopt,
wordt de beweging na korte tijd eenparig.
De onderstaande figuur is een momentopname van de onderste katrol tijdens het bewegen
bij ingeschakeld magneetveld. Dit magneetveld is naar voren gericht, dus loodrecht op het
papier naar de lezer toe, en is gearceerd weergegeven. De lussen zijn genummerd.
C
Teken in onderstaande figuur in die lussen, waarin een elektrische stroom loopt, de
richting van deze stroom. Licht het antwoord toe.
D
Geef in onderstaande figuur aan waar lorentzkrachten op de draadlussen werken en in
welke richting. Licht het antwoord toe.
E
Beredeneer waarom deze beweging eenparig wordt.
De sterkte van de magnetische inductie bedraagt nu 0,36 T. De oppervlakte van één lus is
2,0104 m2 . De weerstand van één lus is 9,3104 .
Tijdens de eenparige beweging schuift een lus in 0.085 s in zijn geheel het magneetveld in.
F
Bereken de stroomsterkte in die lus.
A
B
C
D
E
F
Met de rechterhandregel bepaal je dat de stroom in beide
spoelen aan de 'zichtzijde' naar binnen moet lopen. Vergeet
niet om de voeding te tekenen en om de twee spoelen in serie
aan te sluiten.
 NI
1,26  10  6  2  375  5,0
0
B  0,27 
 0,27 
 0,18 T
d
7,0  10  3
Er is geen fluxverandering in de lussen 1 en 3 en dus loopt
daarin ook geen inductiestroom.
De inductiestroom in 2 is zo gericht dat de lorentzkracht die
daar het gevolg van is tegenwerkt. De lorentzkracht op het 'korte' stukje moet dus wijzen
zoals getekend. Met de linkerhand volgt daaruit de
stroomrichting. Datzelfde kun je doen met lus 4.
Je kunt ook zeggen bij 4: de flux in onze richting
neemt toe en dus moet de inductiestroom zorgen
voor flux van ons af. De rechterhandregel geeft
dan de stroomrichting. M.m. geldt dat ook voor lus
2.
De stroomrichting, samen met de richting van het
magneetveld, bepaalt de richting van de
lorentzkrachten.
Door het blokje gaat het wiel draaien en treedt
fluxverandering op. Door de  ontstaat er een
inductiestroom met tegenwerkende lorentzkracht.
De versnelling van het wiel is daardoor kleiner,
maar de snelheid neemt toe, met nog grotere
inductiestroom en lorentzkracht. Maar kleinere
resulterende kracht en dus kleinere toename van
de snelheid. Dit gaat door totdat de resulterende
kracht nul is. Dan is de snelheid constant en de beweging eenparig.
We nemen als nulpunt het moment dat lus 4 het veld ingaat. Dan loopt er gedurende 0,085 s
een constante inductiestroom ten gevolge van
  0,36  2,0  10  4
U ind 

 8,47  10  4 V
t
0,085
, en dus
4
U 8,47  10
I

 4  0,91 A
R
9
,
3

10
is
.
We nemen aan dat de ruimte tussen de lussen verwaarloosbaar is.
Na die 0,085 s zit de lus geheel in het veld en is er geen inductiestroom meer. Na 0,019 s
weer wel, maar loopt de stroom de andere kant uit:
A
B
C
CENTRALE
Een centrale G produceert een wisselspanning van 2700 V, 50 Hz effectief. Via de
transformatoren en de niet getekende aan- en afvoerkabels is de centrale verbonden met de
verbruikers. De transformatoren mag je als ideaal beschouwen. Ook de weerstanden van de
aansluitkabels verwaarlozen we in eerste instantie.
Bereken op welke spanning de verbruiker aangesloten zal zijn onder de genoemde
benaderingen.
Teken de grafiek van de spanning van de verbruiker als functie van de tijd voor tenminste 2
periodes.
De weerstand tussen T1 en T2 bedraagt 20,0 . Het maximaal door de centrale geleverde
vermogen bedraagt 16,20 MW.
Bereken het vermogen dat door de verbruiker maximaal kan worden afgenomen
Uitwerking:
A
B
Uverbruiker = 2700 × 40 : 30 : 20 = 180 V
De periode is 0,020 s. Je moet dus twee sinussen tekenen, elk 0,020 s lang. Voor het
maximum en minimum moet je niet 180 V nemen, want dat is de effectieve waarde. De
topwaarde van de spanning is 180 × 2 = 255 V.
C
Uit trafo T1 komt 16,20 MW bij een spanning van 2700 × 40 V. Dan is de stroomsterkte
daar te berekenen via: P = I × U  16,20106 = I × 2700 × 40  I = 150 A.
Er gaat aan vermogen verloren P = I2R = 1502 × 20 = 0,45 MW. Over blijft 15,75 MW en dat
komt zonder verdere verliezen bij de gebruiker.
A
B
C
A
B
SPOEL
Een spoel vangt een flux op die in de loop van de tijd verandert volgens de grafiek.
Voor 6 s < t < 8 s is de functie van de flux in de grafiek gegeven.
De verandering van de flux is te wijten aan een verandering van de magnetische inductie B.
Het aantal windingen van de spoel is 10.000 en de gemiddelde oppervlakte van de spoel is
30 cm2.
De richting van de flux in de spoel naar ons toe, naar voren, noemen we positief.
De richting waarin de spoel gewikkeld is, is door een stippellijn op de voorkant aangegeven.
Bepaal de maximale grootte van de magnetische inductie B.
Teken de inductiespanning over de spoel als functie van de tijd.
Leid af welke aansluiting, A of E, positief is t.o.v. de andere op t = 5 s. Zie grafiek.
TRANSFORMATOR
Een lastransformator heeft primair 5000 windingen, secundair 20. De transformator wordt
aangesloten op het net, 230 V, en de primaire stroom is maximaal 16 A.
Bereken de grenswaarde van weerstand in de secundaire kring, waarbij de zekering
doorbrandt.
Leg aan de hand van de formules uit of de weerstand ter voorkoming van doorbranden van
de zekering groter of kleiner moet zijn dan die grenswaarde. Ter verduidelijking: ik verwacht
geen verhaal in de stijl van ‘je snapt wel dat als.....’ , maar een redenering waarin iedere stap
door formules wordt ondersteund.
ENERGIETRANSPORT
Bij de elektriciteitscentrale is de spanning op het hoogspanningsnet Ueff = 380 kV.
De stroomsterkte IMAX is op zeker moment 2000 A. Op dat moment blijkt een spanning van
Ueff = 378 kV bij het transformatorstation van de afnemers gemeten te worden.
De wikkelverhouding is daar 1000:20.
Bereken de weerstand van de betreffende hoogspanningskabels.
Aardlekschakelaar
Ter verduidelijking van de werking van een aardlekschakelaar doen we de volgende proef
die je thuis niet moet uitvoeren!!! Het snoer dat naar een stofzuiger gaat, wikkelen we om
een ijzeren staaf.. Om die ijzeren staaf schuiven we ook een spoel, waarvan de uiteinden
verbonden zijn met een relais. Als er stroom door de spoel loopt, schakelt het relais de
stroom naar de stofzuiger uit.
Leg uit of deze proef het principe van de aardlekschakelaar laat zien.
Antw: ja bij verschil in stroomsterkte ontstaat inductiestroom
a.
b.
DIODE
Hiernaast zie je een schakeling met een
wisselspanningsvoeding, een diode, een weerstand en een
wisselspanningsmeter. De meter wijst 10 V aan. De
frequentie is 50 Hz.
Teken de grafiek van de wisselspanning UAC van de bron als
functie van de tijd. UAC is positief als A positief is t.o.v. C.
Teken in die grafiek met een andere kleur of anderszins
duidelijk, de grafiek van UBC als functie van de tijd.
a.
TAFELPOOT
De tafelpoten van mijn tuintafel zijn gemaakt van een vierkantige aluminium buis met een
zijde van 3,0 cm. De dikte van het aluminium is 1,0 mm.
Hiervan zagen we een 'plak' van
1,0 cm lengte. Deze plak
monteren we op een houten
plankje en laten dat met
constante snelheid door het veld
van een elektromagneet glijden.
Zie de tekening.
In de tekening is aangegeven,
welke de noordpool van de
hoefijzervormige magneet is.
Geef in deze tekening de richting
aan van de magnetische veldlijnen tussen de polen van de magneet.
c.
Als de plak het magneetveld binnengaat,
ontstaat een inductiestroom.
Beredeneer in welke richting die
inductiestroom loopt, linksom of rechtsom.
Bereken de weerstand in de stroomkring.
d.
Als plaats x van de plak, kiezen we de
plaats van de 'voorkant'; zie tekening.
De stroomsterkte I als functie van de
plaats x van de plak kun je meten. Ga er
daarbij van uit dat het magneetveld tussen
de polen homogeen is en daarbuiten
verwaarloosbaar.
Schets de (I,x)-grafiek voor 0  x  6 cm
b.
Uitwerking:
a
zie tekening
b
De flux in 'onze' richting neemt toe. De inductiestroom zal dus veldlijnen 'van ons af' maken.
De richtingsregel zegt dan: stroom rechtsom.
c
De stroom moet door een aluminiumstrip met een lengte van
4·3,0 = 12 cm. Deze strip is 1,0 cm breed en 1,0 mm dik. R = 0,324 m
d
zie grafiek
b
Transformator
Een ideale transformator heeft primair 1200 en secundair
60 wikkelingen, 30 tussen A en B en 30 tussen B en C. Zie
tekening.
De primaire spoel sluiten we aan op een
wisselspanningsvoeding met een Ueff = 380 V. De
frequentie van de wisselspanning is 50 Hz.
De secundaire spoel AC belasten we met een apparaat
met een weerstand van 500 .
Bereken het vermogen dat door het apparaat wordt
opgenomen.
Bereken de stroomsterkte aan de primaire kant.
c
De grafiek van secundaire spanning UAC als functie van de
tijd is getekend, waarbij B is geaard.
Breng de geschikte assen en schaalverdeling aan.
a
d
a
b
c
d
Schets de grafiek van UAB als functie van de tijd in hetzelfde
assenstelsel als de gegeven grafiek van UAC(t).
Uitwerking:
Uit de wikkelverhouding volgt Us,top = 19·2 = 26,9 V
Nu de vraag P = U2/R = 192 / 500 = 0,722 W
Het primair vermogen is even groot, dus
P = IU  0,722 = I·380  I = 1,9·10-3 A
50 Hz geeft een periode van 0,020 s; ook
secundair.
De topwaarde is 26,9 V. A is afwisselend 26,9 V
positief en negatief t.o.v. C.
De helft daarvan t.o.v. B. Dat B geaard is, is
daarbij niet van belang.
a.
b.
TRAFO
Een transformator heeft primair 1200 windingen en secundair 400. Op de secundaire spoel is
een 12 V - 50 W lamp aangesloten die normaal blijkt te branden.
De wisselspanningsfrequentie is 50 Hz.
Bereken de primaire stroomsterkte.
We sluiten op de secundaire zijde van de trafo een meter aan die per ms het opgenomen
vermogen van de lamp registreert.
Teken de grafiek van het geregistreerde vermogen als functie van de tijd voor een periode
van 40 ms.
STAAF OP HELLING
AB en CD zijn evenwijdige
koperen staven, verbonden
door staaf AC. De Dwarsstaaf
PQ wordt zonder beginsnelheid
losgelaten en glijdt met een te
verwaarlozen wrijving
evenwijdig aan AC omlaag. Het
geheel staat in een homogeen
magnetisch veld waarvan B
loodrecht op het grondvlak V
staat en omlaag gericht is. De
staven AB en CD zijn, behalve
door AC en PQ niet geleidend
verbonden.
a.
b.
c.
Beredeneer welke richting de
inductiestroom in PQ heeft.
Beredeneer hoe de kracht gericht is die het magneetveld op de inductiestroom in PQ
uitoefent; geef de krachtrichting precies aan.
Leg uit waarom de versnelling waarmee PQ omlaag glijdt, voortdurend kleiner wordt.
Van alle staven heeft alleen AC weerstand: RAC = 0,40 . De massa van PQ is 0,25 kg. tan 
= 0,75. De afstand tussen AB en CD is 0,50 m. Het magneetveld dat ontstaat door de
inductiestroom beïnvloedt het oorspronkelijke magneetveld niet merkbaar. Als PQ een
snelheid krijgt van 5,0 m/s, glijdt PQ verder éénparig omlaag. B = 0,87 T.
d.
Bereken bij deze eenparige beweging de grootte van de inductiestroom.
INDUCTIEHELLING
Op een helling met een hellingshoek van 10 zijn twee evenwijdige geleiders gemonteerd
op een onderlinge afstand van 1,00 m. Bovenaan zijn deze verbonden door een kabel AB.
Er heerst een homogeen magneetveld, B = 0,50 T, loodrecht op het vlak van de helling. Op
de evenwijdige geleiders wordt een metalen
staaf PQ gelegd, die op t = 0 wordt losgelaten
en naar beneden gaat glijden. De massa van
de staaf PQ is 880 g en de staaf ondervindt
een constante wrijvingskracht van 1,0 N. De
positie van de staaf blijft daarbij loodrecht op
de evenwijdige geleiders.
Zie de tekeningen, ook op het
antwoordblad, waar een boven en
zijaanzicht getekend zijn.
a.
Teken op het antwoordblad in zowel het
boven- als in het zijaanzicht de krachten
die op de staaf PQ werken, terwijl de
staaf schuift.
We letten hierbij wel op de richting van
de krachten, niet op de grootte.
b.
Leid de richting af van de inductiestroom
af en geef deze op het antwoordblad
aan.
c.
Bereken de versnelling op t = 0.
d.
Het blijkt dat de snelheid vanaf t = 10 s
constant is.
Schets op het antwoordblad de (v,t)grafiek en verklaar de vorm van de
grafiek.
e.
f.
Schets op het antwoordblad de grafiek
van de omsloten magnetische flux als
functie van de tijd.
De weerstand van AB = 0,50 . De
overige weerstanden zijn
verwaarloosbaar.
Bereken Uind als de snelheid constant
is.
Uitwerking:
b.
c.
De lorentzkracht moet tegenwerken en dus naar 'links omhoog' wijzen. De richting van het
magneetveld is gegeven. Met de richtingsregel volgt de richting van I.
Op t = 0 is er nog geen snelheid, geen verplaatsing, geen lorentzkracht. De versnelling is
gevolg van de wrijving en de zwaartekrachtscomponent langs het vlak.
F = ma  Fzx - Fw = ma  1,499 - 1,0 = 0,880·a  a = 0,57 m/s2.
Door de versnelling op t = 0 gaat de staaf bewegen. Daarbij neemt de omvatte flux toe en
ontstaat ook een inductiestroom en daarmee tegen werkende lorentzkracht.
Naarmate de snelheid meer toeneemt, nemen ook de inductiestroom en de lorentzkracht toe.
De resulterende kracht wordt kleiner, de versnelling dus ook. Terwijl de snelheid dus
toeneemt, neemt hij steeds minder sterk toe. Kennelijk is op t = 10 s de versnelling al nul
geworden. De snelheid is dan constant.
d.
f.
ab.
d
Als v = 0, is er ook geen . Neemt de snelheid toe, dan neemt daarmee ook de  toe. Hoe
groter de snelheid, des te sneller  toeneemt. Bij constante snelheid is ook die toename
constant.
Als de snelheid constant is, is F = ma = 0. Fzx = Fw + FL  1,499 = 1,0 + BIl.
0,499 = 0,50·Iind·1,00  Iind = 0,998 A  Uind = IR = 0,50 V.