UITWERKINGEN Examentraining elektromagnetisme

UITWERKINGEN Examentraining elektromagnetisme – VWO6-Na1,2
1
UITWERKINGEN Examentraining elektromagnetisme – VWO6-Na1,2
1. a. Buiten een spoel lopen de veldlijnen van de
noordpool naar de zuidpool. Binnen een
spoel lopen ze juist van de zuidpool naar de
noordpool. In nevenstaande figuur moet de
linker zijde van de spoel dus de zuidpool zijn
(en de rechter zijde de noordpool).
b. De richting van de stroom in de spoel kan bepaald worden aan de hand van de
rechterhandregel voor een stroomspoel. De duim moet dan wijzen in de richting
van de veldlijnen binnen de spoel (dus richting de noordpool van de spoel). De
gebogen vingers geven dan de richting van de stroomsterkte aan. Aangezien
de stroom van plus naar min door een elektrische schakeling loopt, zal punt A
de pluspool zijn (en is punt B dus de minpool).
c. Voor een stroomspoel geldt de formule:
N ⋅I
B = µ0 ⋅
l
1550 ⋅ 34 ⋅10−3
B = 4 ⋅ π ⋅10−7 ⋅
= 2,4 ⋅10−4 T
0,28
d. Er geldt weer:
N ⋅I
B = µ0 ⋅
l
N ⋅ 63 ⋅10 −3
N
7,2 ⋅10 −5 = 4 ⋅ π ⋅10 −7 ⋅
→
= 9,1 ⋅10 2 windingen/m
l
l
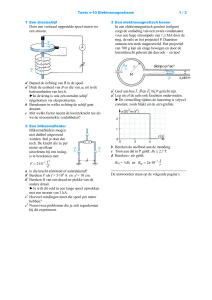
2. a. − Het elektron beweegt langs de cirkel.
In een bepaald punt van de baan kan
deze richting worden bepaald aan de
hand van een raaklijn. De richting van
de stroomsterkte is tegengesteld aan
de bewegingsrichting van het elektron
(een elektrische stroom is immers
vastgesteld als een verplaatsing van
positieve lading).
− De lorentzkracht is gericht naar het
middelpunt van de cirkelbaan. Deze
kracht veroorzaakt immers de voortdurende afbuiging van het elektron.
− Met behulp van de linkerhandregel (wijsvinger in richting stroom, duim in
richting magneetveld en vingers in richting lorentzkracht) kan dan worden
afgeleid dan de magnetische inductie het papier in is gericht.
Zie verder bovenstaande figuur.
b. De snelheid van het elektron in de loop van een cirkelbeweging is constant.
Verder levert de lorentzkracht de middelpuntzoekende kracht. Er geldt:
FL = Fmpz
B ⋅q ⋅v =
m ⋅ v2
r
→
B⋅q =
m⋅v
r
→
v=
B⋅q⋅r
m
UITWERKINGEN Examentraining elektromagnetisme – VWO6-Na1,2
v=
1,2 ⋅10−4 ⋅1,602 ⋅10 −19 ⋅ 0,043
= 9,1⋅105 m/s
−31
9,11 ⋅10
3. De inductiespanning kan berekend worden aan de hand van de wet van Faraday:
∆Φ
U ind = N ⋅
∆t
a. Als de magneet de spoel in beweegt, zal de
inductiespanning toenemen. Als de magneet
volledig in de spoel verdwenen is, zal de inductiespanning gelijk zijn aan 0 V. Er is dan immers
geen fluxverandering. Als de magneet de spoel
weer uit beweegt, neemt de inductiespanning
weer toe, maar nu in negatieve zin.
b. In bovenstaande wet van Faraday is te zien dat
de inductiespanning recht evenredig is met het
aantal windingen van de spoel. Een groter
aantal windingen betekent daarom een grotere
inductiespanning. Zie nevenstaande figuur.
c. Het laten vallen van de magneet vanaf een
grotere hoogte, betekent dat de magneet met
een hogere snelheid door de spoel valt en dat
dus de fluxverandering in een korter tijdsbestek
plaats zal vinden. De inductiespanning zal toenemen en zijn maximale waarde bereiken in een
kortere tijd.
4. Deze opgave kan worden opgelost door het consequent toepassen van enerzijds
de rechterhandregel voor een stroomspoel en anderzijds de wet van Lenz (deze
geeft aan dat een spoel zich altijd verzet tegen veranderingen). Zie verder
onderstaande figuur.
2
UITWERKINGEN Examentraining elektromagnetisme – VWO6-Na1,2
3
5. a. In punt A bevindt zich een positieve lading. Deze wordt afgestoten door de
positieve plaat en aangetrokken door de negatieve plaat. De elektrische kracht
is daarom gericht naar rechts.
b. Voor het elektrisch veld geldt:
F
E= e
q
2,00 ⋅ 10−6
= 3,3 ⋅ 105 N/C
−12
6,0 ⋅ 10
c. Aangezien er in deze situatie sprake is van een homogeen veld tussen de twee
platen van een plaatcondensator, zal de elektrische veldsterkte in punt B gelijk
zijn aan die in punt A. De elektrische kracht in punt B zal daarom ook gelijk zijn
aan de elektrische kracht in punt B.
d. De grootte van de elektrische kracht van de lading in punt C zal de helft zijn van
die in punt A. De lading is immers qua grootte gehalveerd ( Fe = q ⋅ E ). De
richting van de kracht op deze lading zal omgekeerd zijn. Dit vanwege de
negatieve lading.
E=
6. a. De snelheid zal in ieder geval toe moeten nemen omdat het elektron versneld
wordt vanaf de positieve plaat A naar de negatieve plaat B. Er geldt:
q ⋅ U AB = ∆Ek
∆Ek = 1,602 ⋅10 −19 ⋅ 25 = 4,005 ⋅10 −18 J (= 25 eV)
De kinetische energie in punt B zal daarom zijn: Ek ,B = 60 + 25 = 85 eV
b. Er geldt weer:
q ⋅ U PQ = ∆Ek
q ⋅ U PQ =
1
1
2
2
⋅ m ⋅ vB − ⋅ m ⋅ vC
2
2
1
1,602 ⋅10 −19 ⋅ U PQ = 85 ⋅1,602 ⋅10 −19 − ⋅ 9,11 ⋅10 −31 ⋅ 4,2 ⋅10 6
2
(
)
2
→
U PQ = 35 V
7. a. Voor de stroomsterkte geldt:
−
t
I (t ) = I (0 ) ⋅ e R⋅C
Op tijdstip t = 0 s staat de volledige spanning over de weerstand. De startstroomsterkte kan dan berekend worden met de wet van Ohm:
U
24
I= =
= 0,0051 A
R 4,7 ⋅103
De stroomsterkte op tijdstip t = 6,0 s bedraagt dan:
−
6,0
4 , 7⋅103 ⋅680⋅10− 6
I (6,0 ) = 0,0051 ⋅ e
= 7,8 ⋅10 −4 A
b. Voor het oplaadproces van de condensator geldt qua spanning:
t
−


U (t ) = U bron ⋅ 1 − e R⋅C 


6,0
−


3
−6
U (6,0 ) = 24 ⋅ 1 − e 4,7⋅10 ⋅680⋅10  = 20 V




UITWERKINGEN Examentraining elektromagnetisme – VWO6-Na1,2
c. Het tijdstip waarop de stroomsterkte 2,5 mA bedraagt kan berekend worden
met dezelfde formule zoals ook gebruikt in onderdeel a:
I (t ) = I (0 ) ⋅ e
−3
−
t
R⋅C
−
t
4 , 7⋅103 ⋅680⋅10− 6
2,5 ⋅10 = 0,0051 ⋅ e
→ t = 2,3 s
(uitstekend te berekenen met behulp van de “intersect”-optie op de grafische
rekenmachine).
4