Moment

Beginnen met Construeren
Module ribBMC01c
Opleiding: Bouwkunde / Civiele techniek / ROP
Propadeuse, kernprogramma 1e kwartaal
Week 04 en week 05
Theorie:
Momentstelling evenwichtsvoorwaarden
Onderwerp: Dwarskrachtenlijn (D-lijn) en momentenlijn (M-lijn)
Bereken de Momenten en teken M-lijnen van de liggers
Opdracht: Bereken de dwarskrachten en teken de D-lijn van liggers
Boek:
F.Vink, hst. 8 en 9 + opgaven
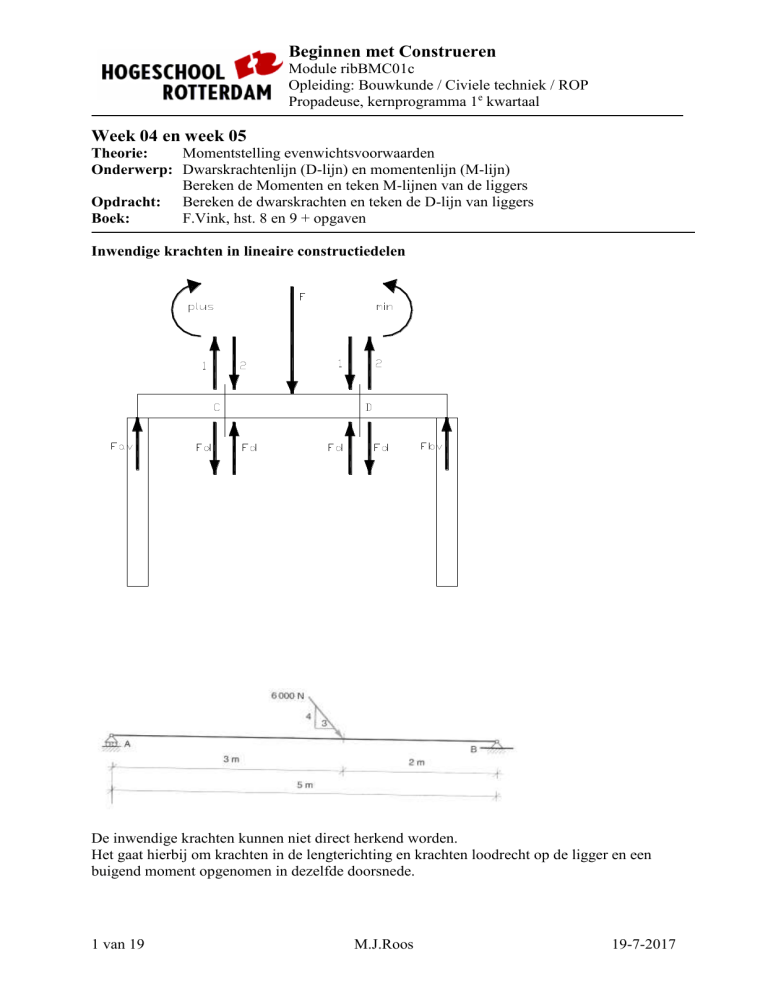
Inwendige krachten in lineaire constructiedelen
De inwendige krachten kunnen niet direct herkend worden.
Het gaat hierbij om krachten in de lengterichting en krachten loodrecht op de ligger en een
buigend moment opgenomen in dezelfde doorsnede.
1 van 19
M.J.Roos
19-7-2017
Beginnen met Construeren
Module ribBMC01c
Opleiding: Bouwkunde / Civiele techniek / ROP
Propadeuse, kernprogramma 1e kwartaal
Geconcentreerde belasting; inwendige krachten in een snede
Welke krachten werken er op doorsnede P op 1 meter afstand van A ?
Eerst zorgdragen voor uitwendig evenwicht.
Berekening reactiekrachten
ΣM = 0 tov A
-4800 * 3 + FvB * 5 = 0
FvB = 2880 N
ΣFv = 0
-2880 + 4800 – FvA = 0
FvA = 1920 N
ΣFh = 0
-3600 + FhB =0
FhB = 3600 N
Er wordt nu een denkbeeldige snede aangebracht in punt P, het rechterdeel wordt daarbij
weggelaten.
2 van 19
M.J.Roos
19-7-2017
Beginnen met Construeren
Module ribBMC01c
Opleiding: Bouwkunde / Civiele techniek / ROP
Propadeuse, kernprogramma 1e kwartaal
Welke krachten worden er nu door het weggelaten rechterdeel uitgeoefend op het linkerdeel
om in evenwicht te raken ?
Dwarskracht
ΣFv = 0
Om aan de bovengestelde voorwaarde te voldoen, moet er in de doorsnede een verticale
kracht werken groot 1920 N naar beneden gericht.
Deze kracht loodrecht op de staafas wordt nu de dwarskracht genoemd en wordt aangeduid
met de letter V.
Normaalkracht
ΣFh = 0
Op het linkerdeel (roloplegging) werken geen horizontale krachten, er werkt in deze
doorsnede dan ook geen normaalkracht.
Inwendig moment
Aanschouwen we het linkerdeel, dan zien we dat dit linkerdeel gaat roteren.
In de doorsnede moeten dus krachten werken die deze rotatie tegen gaan.
3 van 19
M.J.Roos
19-7-2017
Beginnen met Construeren
Module ribBMC01c
Opleiding: Bouwkunde / Civiele techniek / ROP
Propadeuse, kernprogramma 1e kwartaal
Doordat de ligger door een externe kracht, loodrecht op de doorsnede, wordt gebogen door,
ondergaan de bovenste vezels een verkorting en de onderste vezels een verlenging. Daardoor
wordt op de bovenste vezels een drukkracht en op de onderste vezels een trekkracht
uitgeoefend.
De resultante van deze trek- en drukkrachten vormen samen een koppel dat het inwendige
moment Mp wordt genoemd.
Dit inwendig moment gaat dus de rotatie tegen.
Berekening inwendig moment Mp
ΣM t.o.v P = 0
-1920 * 1 + Mp = 0
Mp = 1920 Nm
Welke krachten werken er op doorsnede Q op 1 meter afstand van B ?
We brengen in de denkbeeldige snede Q de krachten aan die er mogelijkerwijs optreden.
- een (verticale) dwarskracht VQ
- een (horizontale) normaalkracht NQ
- een inwendig moment MQ
4 van 19
M.J.Roos
19-7-2017
Beginnen met Construeren
Module ribBMC01c
Opleiding: Bouwkunde / Civiele techniek / ROP
Propadeuse, kernprogramma 1e kwartaal
Dwarskracht
ΣFv = 0
-1920 + 4800 + VQ = 0
VQ = - 2880 N
Normaalkracht
ΣFh = 0
-3600 – NQ = 0
NQ = -3600 N
Inwendig moment
ΣM = 0 t.o.v. Q = 0
-1920 * 4 + 4800 * 1 + MQ = 0
MQ = 2880 Nm
Het blijkt dat VQ en NQ negatief zijn, dit betekent dat de aangenomen richtingen onjuist zijn
geweest.
Voorbeeld 2
Denkbeeldige snede in punt D en E
5 van 19
M.J.Roos
19-7-2017
Beginnen met Construeren
Module ribBMC01c
Opleiding: Bouwkunde / Civiele techniek / ROP
Propadeuse, kernprogramma 1e kwartaal
Berekening reactiekrachten
ΣM = 0 tov A
-12 -8 * 1.5 + FvB * 4 = 0
FvB = 6 kN
ΣFv = 0
- FvA + 8 – 6 = 0
FvA = 2 kN
ΣFh = 0
-6 + FhA = 0
FhA = 6 kN
Er wordt nu een denkbeeldige snede aangebracht in punt D, het rechterdeel wordt daarbij
weggelaten.
Welke krachten worden er nu door het weggelaten rechterdeel uitgeoefend op het linkerdeel
om in evenwicht te raken ?
Dwarskracht
ΣFv = 0
Om aan de bovengestelde voorwaarde te voldoen, moet er in de doorsnede een verticale
kracht werken groot 2 kN naar beneden gericht.
Deze kracht loodrecht op de staafas wordt nu de dwarskracht genoemd en wordt aangeduid
met de letter V.
Normaalkracht
ΣFh = 0
Op het linkerdeel (inklemming) werken horizontale krachten, er werkt in deze doorsnede dan
ook een normaalkracht.
- 6 + ND = 0
ND = 6 kN
Inwendig moment
Aanschouwen we het linkerdeel, dan zien we dat dit linkerdeel gaat roteren.
In de doorsnede moeten dus krachten werken die deze rotatie tegen gaan.
6 van 19
M.J.Roos
19-7-2017
Beginnen met Construeren
Module ribBMC01c
Opleiding: Bouwkunde / Civiele techniek / ROP
Propadeuse, kernprogramma 1e kwartaal
De resultante van deze trek- en drukkrachten vormen samen een koppel dat het inwendige
moment MD wordt genoemd.
Dit inwendig moment gaat dus de rotatie tegen veroorzaakt door de dwarskrachten en het
uitwendig moment.
Berekening inwendig moment MD
ΣM t.o.v D = 0
-2 * 1 -12 + MD = 0
MD = 14 kNm
Voor punt E geldt.
Normaalkracht
ΣFh = 0
- 6 + 6 + NE = 0
NE = 0 kN
Dwarskracht
ΣFv = 0
-2 + 8 + VE = 0
VE = 6 kN
Berekening inwendig moment ME
ΣM t.o.v E = 0
-2 * 2 -12 + 8 * 0.5 + ME = 0
ME = 12 kNm
Grafieken van inwendige krachten
Zie voorbeeld 1
Het is dus mogelijk om op elke plaats van de ligger de inwendige krachten te berekenen. Om
in één oogopslag te kunnen zien hoe het verloop van de inwendige krachten in de constructie
is worden ze in grafieken weergegeven
Deze grafieken worden onder het belastingschema getekend.
7 van 19
M.J.Roos
19-7-2017
Beginnen met Construeren
Module ribBMC01c
Opleiding: Bouwkunde / Civiele techniek / ROP
Propadeuse, kernprogramma 1e kwartaal
We kiezen een willekeurig punt X tussen A en de kracht. X is variabel.
ΣFv = 0
-1920 + VX = 0
VX = 1920 N
In het antwoord komt de variabel X niet meer voor.
De dwarskracht is dus niet afhankelijk van X en heeft dus een constante waarde op het deel
links van de puntkracht.
ΣFh=0
In het beschouwde deel is geen horizontale kracht. De normaalkracht is dus nul.
ΣM t.o.v X = 0
-1920 * x + MX = 0
MX = 1920 * x
Mx is dus wel afhankelijk van de variabele x.
Mx wordt groter als x groter wordt.
Het moment kan dus beschouwd worden als een functie van de afstand.
Het moment kan dus worden genoteerd als M(x): het moment als functie van x.
8 van 19
M.J.Roos
19-7-2017
Beginnen met Construeren
Module ribBMC01c
Opleiding: Bouwkunde / Civiele techniek / ROP
Propadeuse, kernprogramma 1e kwartaal
Het punt X rechts van de puntlast
ΣFv = 0
-1920 + 4800 + VX = 0
VX = - 2880 N
De dwarskracht is ook hier constant, maar negatief. Hij moet dus aan de andere zijde van de
nullijn getekend worden.
ΣM t.o.v X = 0
-1920 * x + 4800 * (x – 3) + MX = 0
MX = - 2880 * x + 14400
Het moment is ook nu lineair afhankelijk van x. De grafiek gaat echter niet door de
oorsprong, maar snijdt de verticale as bij 14400 Nm.
De richtingscoefficient is – 2880 (was 1920). De grafiek vertoont op de plaats van de puntlast
een knik.
Het moment is maximaal op de plaats van de puntlast, dus als x = 3.
De waarde kan worden uitgerekend met het functievoorschrift van het linkerdeel;
Mmax = M(3) = 1920 * 3 = 5760 Nm
ΣFh=0
Aangenomen was dat de normaalkracht van de snede af gericht was. Het antwoord is negatief,
dus de kracht is naar de snede toe gericht.
Er heerst in het liggerdeel rechts van de puntlast dan een drukkracht van 3600 N
9 van 19
M.J.Roos
19-7-2017
Beginnen met Construeren
Module ribBMC01c
Opleiding: Bouwkunde / Civiele techniek / ROP
Propadeuse, kernprogramma 1e kwartaal
Verdeelde belasting
10 van 19
M.J.Roos
19-7-2017
Beginnen met Construeren
Module ribBMC01c
Opleiding: Bouwkunde / Civiele techniek / ROP
Propadeuse, kernprogramma 1e kwartaal
Reactiekrachten
ΣM tov A = 0
-10 * 5 * 2.5 -10 * 2 * 6 + FvB * 5 = 0
FvB = 49 kN
ΣFv = 0
70 – 49 – FvA = 0
FvA = 21 kN
De inwendige krachten in punt C op 1 m vanaf A
Snede aanbrengen in punt C, rechterdeel weglaten.
ΣFh = 0
Er zijn geen horizontale krachten, Nc = 0
ΣFv = 0
-21 + 10 * 1 + Vc = 0
Vc = 11 kN
ΣM t.o.v. C = 0
-21 * 1 + 10 * 1 * 0.5 + Mc = 0
Mc = 16 kNm
De inwendige krachten in punt D op 2 m vanaf A
Snede aanbrengen in punt D, rechterdeel weglaten
ΣFh = 0
Er zijn geen horizontale krachten, ND = 0
ΣFv = 0
-21 + 10 * 2 + VD = 0
VD = 1 kN
ΣM t.o.v. D = 0
11 van 19
M.J.Roos
19-7-2017
Beginnen met Construeren
Module ribBMC01c
Opleiding: Bouwkunde / Civiele techniek / ROP
Propadeuse, kernprogramma 1e kwartaal
-21 * 2 + 10 * 2 * 1 + MD = 0
MD = 22 kNm
Het blijkt dus dat voor een willekeurige doorsnede op afstand x vanaf A geldt:
ΣFh = 0
Er zijn geen horizontale krachten, Nx = 0
ΣFv = 0
-21 * 10 * x + Vx = 0
Vx = 21 – 10x kN
ΣM t.o.v. X = 0
-21 * x + 10 * x * x/2 + Mx = 0
Mx = 21x – 5x2 kNm
Mx = - 5x2 + 21x kNm
De V-lijn is nu een lineaire functie van x.
De M-lijn is nu een kwadratische functie van x.
Voor het liggerdeel rechts van oplegging B
(let op negatieve snede. De positief inwendige krachten werken dus tegengesteld aan de asrichtingen)
ΣFv = 0
-Vx + 10 * (7 – x) = 0
12 van 19
M.J.Roos
19-7-2017
Beginnen met Construeren
Module ribBMC01c
Opleiding: Bouwkunde / Civiele techniek / ROP
Propadeuse, kernprogramma 1e kwartaal
Vx = 70 – 10x kN
ΣMx = 0
-Mx – (7 – x)/2 * 10 * (7 – x) = 0
Mx = - 5x2 + 70x – 245 kNm
13 van 19
M.J.Roos
19-7-2017
Beginnen met Construeren
Module ribBMC01c
Opleiding: Bouwkunde / Civiele techniek / ROP
Propadeuse, kernprogramma 1e kwartaal
Tekenen van een parabolische momentenlijn
In beide gevallen moeten de momenten aan het einde van de parabool bekend zijn.
In beide gevallen moet het moment in het midden van de ligger bekend zijn,
De lijn door Mc evenwijdig aan de lijn Ma – Mb is de raaklijn aan de parabool in Mc.
In het 1e figuur zijn de raaklijnen getekend aan de parabool in de punten Ma en Mb.
Deze snijden elkaar op de verticale lijn door Mc waarbij de afstanden Mc – D en Mc – E
gelijk zijn.
In het 2e figuur zijn 2 parallellogrammen, hierin de beide halve parabolen opgenomen,
getekend.
Deze parallelogrammen zijn beiden in horizontale- en in verticale richting in vier gelijke
delen getekend.
14 van 19
M.J.Roos
19-7-2017
Beginnen met Construeren
Module ribBMC01c
Opleiding: Bouwkunde / Civiele techniek / ROP
Propadeuse, kernprogramma 1e kwartaal
Door de verticale verdeling wordt vanaf de horizontale verdeling stippellijnen getekend naar
punt Mc.
De gemarkeerde snijpunten zijn nu de punten van de parabool.
Tekensymbolen
De kurkentrekkerregel.
z- as
positief
Assenstelsel in een ligger
De x –as in lengterichting van de ligger.
De y – as loodrecht op de lengteas
De z-as naar beneden gericht.
Positieve asrichtingen
In het x-z vlak bevindt zich dan de langsdoorsnede van de ligger.
In het y-z vlak bevindt zich dan de dwarsdoorsnede.
Op het linkerdeel van de snede werken de positief genoemde inwendige krachten in de
positieve richting van de assen, daarom heet dit deel de positieve doorsnede.
De positief genoemde inwendige krachten op het rechterdeel werking in negatieve richting
van de assen, dit deel wordt daarom de negatieve doorsnede genoemd
15 van 19
M.J.Roos
19-7-2017
Beginnen met Construeren
Module ribBMC01c
Opleiding: Bouwkunde / Civiele techniek / ROP
Propadeuse, kernprogramma 1e kwartaal
-
Voor het buigend moment wordt in een grafiek een boogje geplaatst dat de kromming
van de ligger weergeeft.
De dwarskracht wordt weergegeven door een haak die de vervorming symboliseert
Een trekkracht; twee pijltjes van elkaar afgericht.
Een drukkracht; twee pijltjes naar elkaar toegericht.
Geconcentreerde belasting
F
A
½l
½l
Fb
Fa
16 van 19
B
M.J.Roos
19-7-2017
Beginnen met Construeren
Module ribBMC01c
Opleiding: Bouwkunde / Civiele techniek / ROP
Propadeuse, kernprogramma 1e kwartaal
ΣM to.v. A = 0
- F * ½ l + Fb * l = 0
Fb * l = ½ Fl
Fb = ½ F
ΣFv = 0
F – ½ F – Fa = 0
Fa = ½ F
Maximaal moment
M=½F*½l
M = ¼ Fl
Gelijkmatig verdeelde belasting
A
B
q kN/m
L
Fa
Fb
ΣM to.v. A = 0
- q * l * ½ l+ Fb * l = 0
Fb * l = q * l * ½ l
Fb = ½ ql
ΣFv = 0
q * l – ½ ql – Fa = 0
Fa = ½ ql
Maximaal moment
M = (½ ql)/2 * ½ l
M = 1/8 ql2
17 van 19
M.J.Roos
19-7-2017
Beginnen met Construeren
Module ribBMC01c
Opleiding: Bouwkunde / Civiele techniek / ROP
Propadeuse, kernprogramma 1e kwartaal
18 van 19
M.J.Roos
19-7-2017
Beginnen met Construeren
Module ribBMC01c
Opleiding: Bouwkunde / Civiele techniek / ROP
Propadeuse, kernprogramma 1e kwartaal
Buigend moment en momentenlijn
Oplegreacties zijn afhankelijk van de belasting
Het deel links van de snede zal ten opzichte van het rechter gedeelte bovenstaand figuur
willen aannemen.
De snede wil dus openbuigen.
Dit komt door het zogenaamd buigend moment
Mx = Fav * x
Zonder de snede blijft de constructie intact, de vezels bieden dan voldoende weerstand aan het
buigend moment Mx.
Hoe groter F, hoe groter Mx. De kans op gapingen en scheuren wordt dan ook groter, zonder
dat wij hiervoor een snede hoeven aan te brengen.
Tekenafspraak
We rekenen een buigend moment positief als de vezels onderin de balk op trek worden belast.
19 van 19
M.J.Roos
19-7-2017