Straaljager

317492443
Straaljager
v  at  t 
v 270 / 3, 6

 2, 08  2,1 s
a
36
.
s  12 at 2  12 36  2, 082  77,9 m = 78 m
veind  v0
270 / 3, 6  0
t
2, 08  78 m
2
2
(alleen bij een eenparig versnelde beweging (a constant)
of: s  vgemt 
mag je de gemiddelde snelheid zo uitrekenen.)
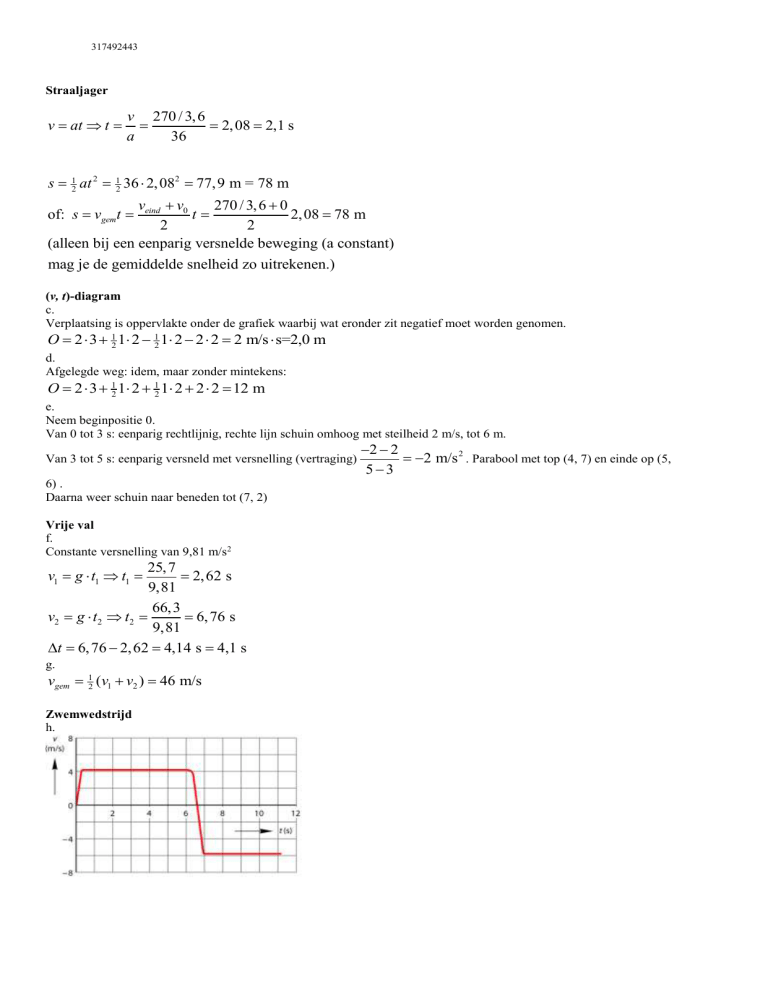
(v, t)-diagram
c.
Verplaatsing is oppervlakte onder de grafiek waarbij wat eronder zit negatief moet worden genomen.
O  2  3  12 1 2  12 1 2  2  2  2 m/s  s=2,0 m
d.
Afgelegde weg: idem, maar zonder mintekens:
O  2  3  12 1 2  12 1 2  2  2  12 m
e.
Neem beginpositie 0.
Van 0 tot 3 s: eenparig rechtlijnig, rechte lijn schuin omhoog met steilheid 2 m/s, tot 6 m.
Van 3 tot 5 s: eenparig versneld met versnelling (vertraging)
6) .
Daarna weer schuin naar beneden tot (7, 2)
Vrije val
f.
Constante versnelling van 9,81 m/s2
25, 7
 2, 62 s
9,81
66,3
v2  g  t2  t2 
 6, 76 s
9,81
t  6, 76  2, 62  4,14 s  4,1 s
v1  g  t1  t1 
g.
vgem  12 (v1  v2 )  46 m/s
Zwemwedstrijd
h.
2  2
 2 m/s 2 . Parabool met top (4, 7) en einde op (5,
53
317492443
Koord
De zwaartekracht wordt opgeheven door beide verticale componenten van de spankracht.
spankrachten wijzen langs het touw schuin omhoog.
  sin 1 (1,5 / 2)  48, 6o
cos  
1
2
1,5
Doe
2
1
Fz
20  9,81
 Fs  2
 148 N=1,5 102 N
o
Fs
cos 48, 6
Spin
j.
75 mg = 75.10-6 kg komt overeen met 7,35.10-4 N
Hoek α is nu 55°
cos (55°) = ½ Fg / Fspan
Fspan = 6,4.10-4 N
k.
Fspan max = 9.10-4 N
Ftrek = Fg tan (40 °)
cos (αmax) = ½ Fg / Fspan max
αmax = 66°
De totale hoek is 2αmax = 132 °
Hijskraan
l.
Strategie: bekijk de krachten op de twee massa’s samen; delen door de gezamenlijke massa levert de versnelling op (voor
zowel de linker die naar beneden wijst als voor de rechter die langs de helling schuin naar boven wijst); met de tijd
bereken je de verplaatsing.
1.
2.
Op de twee massa’s en het koord samen werken:
de zwaartekracht op de linkermassa: Fz ,links  mg ;
de component langs het vlak van de zwaartekracht op de linkermassa: Fz , rechts , parallel  mg sin 30  12 mg .
Fres 1
 g.
2m 4
Verplaatsing na 2 s: s(t )  12 at 2  12 14 gt 2  14 g  22  12 g  4,9 m = 5 m
Samen: Fres  12 mg . De versnelling van het geheel is dan a 
317492443
Evenwicht
m.
Voor de balk geldt: som der krachten is nul. Bovendien: T.o.v. bijvoorbeeld S2 is de
som der krachten nul.
M linksom, S2  Flinkerstaaf op balk  rS2 naar linkerstaaf  Flinkerstaaf op balk  1
M rechtsom, S2  Fz op balk  rS2 naar balk  15, 0  9,81 3
M linksom, S2  M rechtsom, S2  Flinkerstaaf op balk  441, 45 N = 4,4 102 N
Frechterstaaf op balk  Flinkerstaaf op balk  Fz op balk  441, 45  15, 0  9,81  588, 6 N = 5,9 102 N
BrievenWeger
n.
Zet de brief in de sleuf van 20 g. Indien de BrievenWeger niet kantelt dan moet men slechts € 0,39 plakken en is de brief
dus niet juist gefrankeerd. Kantelt hij wel, dan moet hij de brief in de sleuf van 50 g zetten. Kantelt de BrievenWeger nu
ook, dan is de massa groter dan 50 g en moet men meer dan € 0,78 plakken en is de brief niet juist gefrankeerd. Alleen als
hij nu niet kantelt weet je dat de massa van de brief tussen 20 en 50 g ligt, dus dat je € 0,78 moet plakken en dat de brief
juist is gefrankeerd.
o.
• Pas de momentwet toe, met K als kantelpunt.
• Er moet gelden F z,22 * r 1 = F nieuw * r 2
• r 1 = 41 mm en r 2 = 14 mm
• F z = m.g = m.9,81
• 0,022 * 9,81 * 41 = m * 9,81 * 14
• m = 64 kg
p.
• Als de BrievenWeger op deze manier schuin staat, zal de afstand van K tot de werklijn van F z, gehele BrievenWeger groter
worden.
• De afstand van K tot de werklijn van F z,brief zal kleiner worden.
• Met toepassen van de momentenwet is voor kantelen een grotere massa van de brief nodig.
• Dus: meer dan 22 gram.