2 1 1 0 0 2 , b = −1 1 1

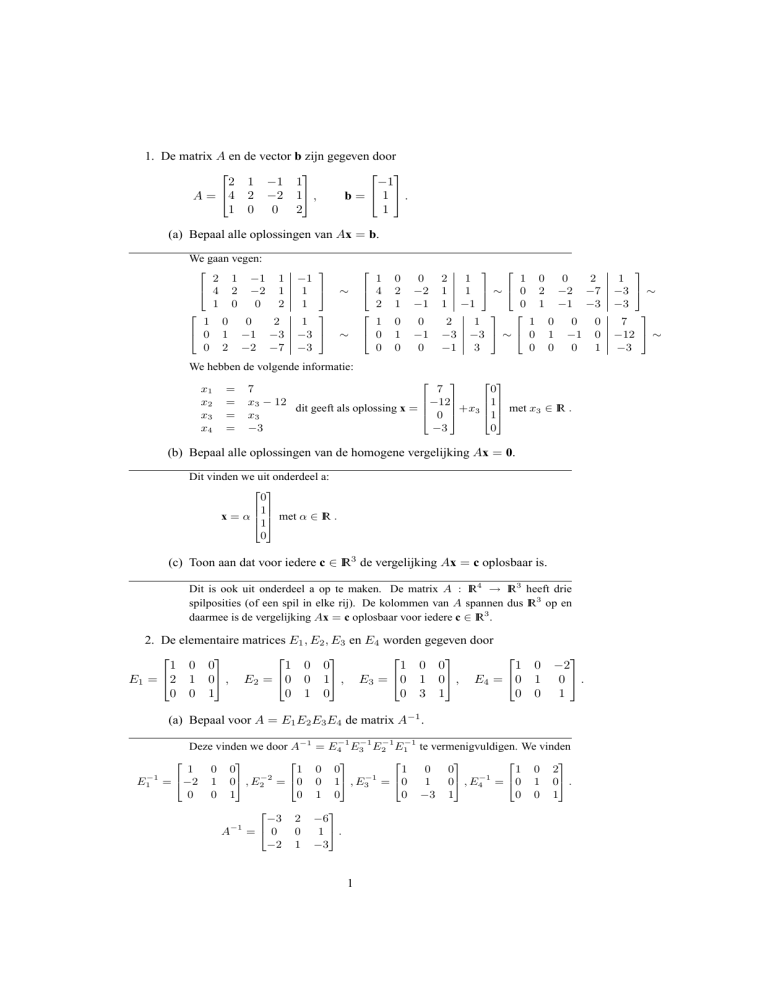
1. De matrix A en de vector b zijn gegeven door


 
2 1 −1 1
−1
A = 4 2 −2 1 ,
b =  1 .
1 0 0 2
1
(a) Bepaal alle oplossingen van Ax = b.
We gaan vegen:

2 1 −1 1
 4 2 −2 1
1 0
0
2

1 0
0
2
 0 1 −1 −3
0 2 −2 −7

−1
1 
1

1
−3 
−3

∼
∼
1
 4
2

1
 0
0
0
2
1
0
−2
−1
0
1
0
0
−1
0
 
1 0
0
2
1
1  ∼  0 2 −2 −7
0 1 −1 −3
−1
 
2
1
1 0
0
0
−3 −3  ∼  0 1 −1 0
−1
3
0 0
0
1
2
1
1
We hebben de volgende informatie:
x1
x2
x3
x4
=
=
=
=


 
7
7
0
−12
1
x3 − 12



 met x3 ∈ IR .
dit geeft als oplossing x = 
+x
x3
0  3 1
−3
−3
0
(b) Bepaal alle oplossingen van de homogene vergelijking Ax = 0.
Dit vinden we uit onderdeel a:
 
0
1

x = α 
met α ∈ IR .
1
0
(c) Toon aan dat voor iedere c ∈ IR3 de vergelijking Ax = c oplosbaar is.
Dit is ook uit onderdeel a op te maken. De matrix A : IR4 → IR3 heeft drie
spilposities (of een spil in elke rij). De kolommen van A spannen dus IR3 op en
daarmee is de vergelijking Ax = c oplosbaar voor iedere c ∈ IR3 .
2. De elementaire matrices E1 , E2 , E3 en E4 worden gegeven door







1 0 0
1 0 0
1 0 0
1
E1 = 2 1 0 , E2 = 0 0 1 , E3 = 0 1 0 , E4 = 0
0 0 1
0 1 0
0 3 1
0

0 −2
1 0 .
0 1
(a) Bepaal voor A = E1 E2 E3 E4 de matrix A−1 .
E1−1
Deze vinden we door A−1 = E4−1 E3−1 E2−1 E1−1





1
0 0
1 0 0
1
= −2 1 0 , E2−2 = 0 0 1 , E3−1 = 0
0
0 1
0 1 0
0


−3 2 −6
0
1 .
A−1 =  0
−2 1 −3
1
te vermenigvuldigen. We vinden



0
0
1 0 2
1
0 , E4−1 = 0 1 0 .
−3 1
0 0 1

1
−3  ∼
−3

7
−12  ∼
−3
E1
(b) Zij B =
0
−1
E2
E1
−1
. Toon aan dat B =
E3
0
−E1−1 E2 E3−1
.
E3−1
Omdat B vierkant is, is het voldoende B en B −1 met elkaar te vermengvuldigen
I 0
en op te merken dat het resultaat gelijk is aan de eenheidsmatrix
.
0 I
3.
Zij
 
1
v1 = 0 ,
1
 
1
v2 = 1 ,
0
 
0
v3 = 1 ,
1
 
1
e1 = 0 ,
0
 
3
c = 2 .
1
Van de lineaire transformatie T : IR3 → IR3 is gegeven dat T (v1 ) = v2 , T (v2 ) =
v3 , T (v3 ) = v1 .
(a) Bereken T (e1 ). Hint e1 = 12 (v1 + v2 − v3 ).
T (e1 ) = T ( 12 (v1 + v2 − v3 ) =
1
2
T (v1 ) + T (v2 ) − T (v3 ) =
 
0
Omdat T lineair is. We vinden T (e1 ) = 1.
0
1
2
v2 + v3 − v 1 .
(b) Bepaal de standaard matrix A van de transformatie T .
C C We hebben dat A = [T (e1 ) T (e2 ) T (e3 )]. T (e1 ) hebben we al bij onderdeel
a bepaald. Op dezelfde wijze vinden we dat e2 = 21 (v2 + v3 − v1 ) en e3 =
1
(v1 + v3 − v2 ). We vinden T (e1 ) = e2 , T (e2 ) = e3 en T (e3 ) = e1 . Dus
2

0
A = 1
0
0
0
1

1
0 .
0
(c) Bepaal x zodat T (x) = c.
 
2
Dit lossen we op met onderdeel b en vinden x = 1.
3
4. Zij A(t) de matrix die voor ieder reëel getal t gegeven wordt door


 
t
1
1
−1
A(t) = 1 t + 1 0 , en zij b =  1  .
1
t
1
1
(a) Toon aan dat de determinant van A(t) gelijk is aan t2 + t − 2.
Dit behoeft geen antwoord.
(b) Voor welke waarden van t is A(t) een inverteerbare matrix?
A(t) is inverteerbaar als zijn determinant ongelijk aan nul is. De determinant van
A(t) is gelijk aan nul voor t = 1 en t = −2. Voor de overige waarden van t is A(t)
inverteerbaar.
2
(c) Los de vergelijking A(t)x(t) = b op voor alle waarden van t.
We gaan vegen:


1
 0
0
t
 1
1
1
t+1
t
t
1
1 − t2
1
−1
1−t

−1
1 
1

1

0
−1 − t
1
0
1

∼
∼
1
 1
t

1
 0
0
t
t+1
1
t
1
0

1
1 ∼
−1
1
0
1
1
−1
2 − t − t2

1

0
−1 − t
We moeten de waarden t = −2 en t = 1 apart bekijken. Voor deze waarden is het
stelsel strijdig, dus geen oplossing.
Voor overige waarden van t hebben we


1 t
1
1
 0 1
 ∼
0
−1
0 0 2 − t − t2 −1 − t


t+1
1 t 0 1 − (t+2)(t−1)
 0 1 0

t+1

 ∼
(t+2)(t−1)
t+1
0 0 1
(t+2)(t−1)

1
 0
0

1

 0
0
t
1
0
1
−1
1
0
1
0
0
0
1
1
0
t+1
(t+2)(t−1)
1−

∼
(t2 +1)
t+1
− (t+2)(t−1)
(t+2)(t−1)
t+1
(t+2)(t−1)
t+1
(t+2)(t−1)
De oplossing wordtgegeven door


−3 − t
1
 t+1 
x(t) =
(t + 2)(t − 1)
t+1
5. Bepaal of de onderstaande beweringen juist of onjuist zijn. Indien de bewering
juist is, geef dan een bewijs. Als de bewering onjuist is, geef dan een tegenvoorbeeld. Met A en B worden steeds matrices met reële elementen aangeduid.
(a) A is een 5 × 4 matrix. Als Ax = 0 géén vrije variabelen heeft, dan heeft
Ax = b voor iedere b ∈ IR5 precies één opolssing.
De matrix A heeft maar 4 kolommen in IR5 en deze kunnnen dus nooit IR5 opspannen. Een tegenvoorbeeld wordt gegeven door


 
1 0 0 0
0
0 1 0 0
0


 

 
A=
0 0 1 0 en b = 0 .
0
0 0 0 1
0 0 0 0
1
(b) Voor alles m × m(m > 1) matrices A en B geldt: Als A, B en A + B
inverteerbaar zijn, dan is (A + B)−1 = A−1 + B −1 .
Neem voor A en B de 2 × 2 eenheidsmatrices en het is onjuist.
(c) Voor alles m × m(m > 1) matrices A en B geldt dat uit AB = 0 en A 6= 0
volgt dat B = 0.
Onjuist: Neem A =
1
0
0
0
en B =
0
0
3
0
.
1



(d) Zij A een m×n matrix en {v1 , . . . , vp } vectoren in IRn . Als {Av1 , . . . , AVp }
lineair onafhankelijk zijn, dan zijn ook {v1 , . . . , vp } lineair onafhankelijk.
Juist. We bewijzen dit vanuit het ongerijmde. Stel {v1 , . . . , vp } lineair afhankelijk.
Dan zijn er α1 , . . . , αp niet allen gelijk aan nul zodat
α1 v1 + · · · αp vp = 0.
Dan geldt ook
A(α1 v1 + · · · αp vp ) = A0 = 0.
maar dit is hetzelfde als
α1 Av1 + · · · αp Avp = 0.
Dus er is een lineaire combinatie van Av1 , . . . , Avp die nul oplevert en dus zijn de
vectoren {Av1 , . . . , Avp } lineair afhankelijk. Dit is in tegenspraak met de aanname
dus {v1 , . . . , vp } zijn lineair onafhankelijk.
(e) Voor iedere matrix A geldt dat det AAT ≥ 0.
Juist: det AAT = det A · det AT = det A · det A = (det A)2 , en dat is altijd
≥ 0.
(f) Ieder systeem van twee vergelijking met twee onbekenden dat een oplossing heeft, kan opgelost worden met de regel van kramer.
Onjuist. Dit systeem kan geschreven worden als Ax = b. Neem b = 0. Dan heeft
dit systeem altijd een oplossing. Neem nu A zodat det A = 0. Dit systeen kan niet
opgelost worden met de regel van Cramer.
6. Zij V de vectorruimte die bestaat uit alle veeltermen (=polynomen) p(t) van
de graad ten hoogste 3 met de gewone puntsgewijze optelling en scalaire vermenigvuldiging. Zij W = {p(t) ∈ V : p(1) = 0}. Toon aan dat W een lineaire
deelruimte van V is.
Om te na te gaan dat W een lineaire deelruimte van de vectorruimte(!) V is moeten we
drie dingen nagaan:
• Het nulpolynoom p(t) ≡ 0 zit in W . Voor dit polynoom geldt zeker p(1) = 0. Dus
inderdaad p(t) ∈ W
• Stel p1 (t) en p2 (t) zijn elementen van W . Voor het polynoom p(t) = p1 (t)+p2 (t)
geldt: p(1) = p1 (1) + p2 (1) = 0. Dus p(t) ∈ W .
• Stel q(t) ∈ W . Bekijk nu p(t) = c · q(t) voor c ∈ IR. Voor p(t) geldt p(1) =
c · q(1) = 0. Dus p(t) ∈ W .
Dus W is een lineaire deelruimte van V .
4