Hoofdstuk 6: Driehoeksmeting

Hoofdstuk 1: Tweedegraadsfuncties
Hoofdstuk 1: Tweedegraadsfuncties
1.1 Grafieken van de functies y = ax²
boek p.8-12
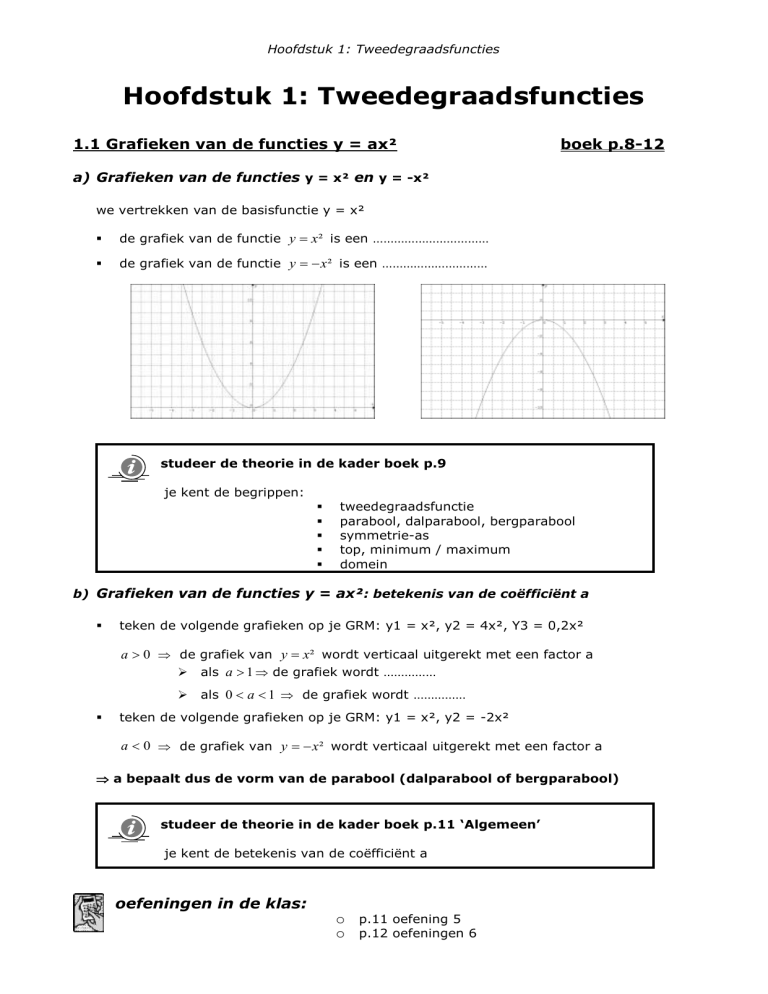
a) Grafieken van de functies y = x² en y = -x²
we vertrekken van de basisfunctie y = x²

de grafiek van de functie y  x² is een ……………………………

de grafiek van de functie y   x ² is een …………………………
studeer de theorie in de kader boek p.9
je kent de begrippen:





tweedegraadsfunctie
parabool, dalparabool, bergparabool
symmetrie-as
top, minimum / maximum
domein
b) Grafieken van de functies y = ax²: betekenis van de coëfficiënt a

teken de volgende grafieken op je GRM: y1 = x², y2 = 4x², Y3 = 0,2x²
a  0  de grafiek van y  x² wordt verticaal uitgerekt met een factor a
 als a  1  de grafiek wordt ……………


als 0  a  1  de grafiek wordt ……………
teken de volgende grafieken op je GRM: y1 = x², y2 = -2x²
a  0  de grafiek van y   x ² wordt verticaal uitgerekt met een factor a
 a bepaalt dus de vorm van de parabool (dalparabool of bergparabool)
studeer de theorie in de kader boek p.11 ‘Algemeen’
je kent de betekenis van de coëfficiënt a
oefeningen in de klas:
o p.11 oefening 5
o p.12 oefeningen 6
Hoofdstuk 1: Tweedegraadsfuncties
1.2 Grafieken van de functies y = a.(x-d)²+e
boek p.13-17
a) Grafieken van de functies y = ax²+e: betekenis van de coëfficiënt e
teken de volgende grafieken op je GRM: y1 = 2x², y2 = 2x²+2, Y3 = 2x²-1

e  0  de grafiek van y  ax² wordt naar …………… verschoven over een afstand ……

e  0  de grafiek van y  ax² wordt naar …………… verschoven over een afstand ……
studeer de theorie in de kader boek p.13 ‘Algemeen’
je kent de betekenis van de coëfficiënt e
b) Grafieken van de functies y = a.(x-d)²: betekenis van de coëfficiënt d
teken de volgende grafieken op je GRM: y1 = 3x², y2 = 3.(x-1)², Y3 = 3.(x+1)²

d  0  de grafiek van y  ax² wordt naar …………… verschoven over een afstand ……

d  0  de grafiek van y  ax² wordt naar …………… verschoven over een afstand ……
studeer de theorie in de kader boek p.15 ‘Algemeen’
je kent de betekenis van de coëfficiënt d
c) Samengevat: grafieken van de functies y = a.(x-d)²+e
Je bekomt de grafiek van de functie y  ax  d ²  e uit de basisgrafiek
y  x² door volgende stappen uit te voeren:




de grafiek vertikaal uitrekken met een factor a
de grafiek spiegelen om de x-as als a  0
de grafiek verschuiven naar boven (als e  0 ) of naar onder (als e  0 )
over een afstand |e|
de grafiek verschuiven naar rechts (als d  0 ) of naar links (als d  0 )
over een afstand |d|
De grafiek van y  ax  d ²  e is een …………………

met als symmetrie-as: ………….

en als top T(……,……)
oefeningen in de klas:
o
o
o
o
p.13
p.15
p.16
p.17
oefening 9
oefeningen 14 en 15
oefening 18
oefening 19
Extra oefeningen: groene kopie REEKS 1 oefening 1
Hoofdstuk 1: Tweedegraadsfuncties
1.3 Grafieken van de functies y = ax²+bx+c
boek p.18-21
De vergelijking van een parabool kan in twee vormen geschreven worden:
 eerste vorm (met haakjes): y  ax  d ²  e met top T(d,e) en symmetrie-as: x=d

tweede vorm (zonder haakjes): y  ax²  bx  c
(dit is de meest gebruikte vorm)
a) Grafieken van de functies y = ax²+bx+c

De grafiek van y  ax²  bx  c is ook een parabool. Een voorbeeld toont dit aan:
y  5.x  3²  4 stelt een parabool voor met top T (…… , ……) en s.a.: x = ……
gebruik de formule  x  a ² =

y  5.
²  4

werk de haakjes uit (distributiviteit)

voer de bewerkingen met de getallen uit
gebruik eenvoudigere symbolen a, b en c
de vergelijking staat nu in de tweede vorm;
deze vergelijking stelt dezelfde parabool voor als y  5.x  3²  4

Hoe kunnen we nu de vergelijking van de symmetrie-as en top vinden als de parabool
in de 2de vorm ( y  ax²  bx  c ) gegeven is?
Uit het vorige voorbeeld kunnen we afleiden: het symbool b (dat voor de x-term staat)
in de tweede vorm komt overeen met ………………… in de eerste vorm;
dus: …………………………… of
Met de vorige formule kunnen we de vergelijking van de symmetrie-as en de
coördinaten van de top vinden:
eerste vorm: y  ax  d ²  e
symmetrie-as
tweede vorm: y  ax²  bx  c
x=d
T (…… , …………)
top
T ( d, e)
y-coördinaat van de top: vul de
x-coördinaat in vergelijking van
de parabool ( y  ax²  bx  c ) in
Extra oefeningen: groene kopie REEKS 1 oefening 2
Hoofdstuk 1: Tweedegraadsfuncties
b) Verloop van een tweedegraadsfunctie
Met het verloop van een tweedegraadsfunctie bedoelen we het stijgen en dalen van een
functie (of de grafiek van de functie).
Werkwijze om het verloop van tweedegraadsfuncties te onderzoeken:
1. bereken de x-coördinaat van de top met de formule x 
b
2a
2. bereken de y-coördinaat van de top (door de x-coördinaat in het functievoorschrift
uit de opgave in te vullen)
3. onderzoek of we met een bergparabool of een dalparabool te maken hebben:
 als a positief is, dan is het een dalparabool
 als a negatief is, dan is het een bergparabool
4. stel de tabel met het verloop op:
als a positief is:
schets:
x
f(x)
als a negatief is:
schets:
x
f(x)
oefeningen in de klas:
o p.19 oefening 20 (1 en 4)
o p.20 oefeningen 22
Extra oefeningen: groene kopie REEKS 2 oefening 1
c) Extremumproblemen: minimum- en maximumproblemen
Werkwijze om minimum- en maximumproblemen op te lossen:
1. wat onbekend is (gezocht wordt) noem je x
opmerking: als er twee onbekenden zijn, dan stel je voor de tweede onbekende met behulp van de opgave - een formule op waarin x (de eerste onbekende)
voorkomt
2. wat maximaal of minimaal moet zijn noem je y
3. schrijf aan de hand van de opgave een formule voor y waarin x voorkomt
als eindresultaat bekom je een tweedegraadsfunctie in x waarin de termen
gerangschikt zijn volgens dalende graad
4. stel het verloop van y op (een tabel met stijgen en dalen)
5. formuleer het antwoord
Hoofdstuk 1: Tweedegraadsfuncties
voorbeeld van een extremumprobleem: oef.25 p.21
Een rechthoekig huis moet een omtrek hebben van 40 meter. Hoe groot moet de lengte zijn
om een maximale oppervlakte te verkrijgen?
1. wat onbekend is (gezocht wordt) noem je x: ………………………………………
2. wat maximaal of minimaal moet zijn noem je y: ……………………………………
3. schrijf aan de hand van de opgave een formule voor y waarin x voorkomt:
als eindresultaat bekom je een tweedegraadsfunctie in x waarin de termen
gerangschikt zijn volgens dalende graad
4. stel het verloop van y op (een tabel met stijgen en dalen):
5. formuleer het antwoord:
oefeningen in de klas:
o p.21 oefening 25
o p.34 oefening 50
o p.21 oefening 24
Extra oefeningen: groene kopie REEKS 2 oefening 2
Hoofdstuk 1: Tweedegraadsfuncties
1.4 Opstellen van functievoorschriften
boek p.22-25
Eerste soort oefeningen: de top en 1 punt zijn gekend
gebruik de eerste vorm van de vergelijking van de parabool: y  ax  d ²  e
en zoek de waarde van a, d en e
1. uit de coördinaten van de top kunnen we onmiddellijk de waarden van d en e afleiden
(want algemeen weten we: de coördinaten van de top zijn (d,e)
 vervang d en e in de vergelijking van de parabool door de gevonden waarden
2. vul de coördinaten van het gegeven punt in de vergelijking van de parabool in
 je vindt de waarde van a
3. vul de gevonden waarden voor a, d en e in de algemene vergelijking van de parabool in
voorbeeld: p.24 oefening 29(1)
Bepaal het voorschrift van de tweedegraadsfunctie waarvan de grafiek door de oorsprong gaat
en de top T(4,3) is.
We werken met de 1ste vorm van de vergelijking van de parabool: y  ax  d ²  e
1. d =
e=
2. vul de coördinaten van het gegeven punt in en bereken a:
3. het voorschrift van de tweedegraadsfunctie is:
Extra oefeningen: groene kopie REEKS 3 oefening 3
Hoofdstuk 1: Tweedegraadsfuncties
Tweede soort oefeningen: de symmetrie-as en 2 punten zijn gekend
gebruik de eerste vorm van de vergelijking van de parabool: y  ax  d ²  e
en zoek de waarde van a, d en e
1. gebruik de vergelijking van de symmetrie-as die opgegeven is om d te vinden
(want algemeen weten we: de vergelijking van de symmetrie-as is x=d)
 vervang d in de vergelijking van de parabool door de gevonden waarde
2. vul de coördinaten van het eerste punt in de vergelijking van de parabool in
 je vindt een formule waarin a en e staan: schrijf deze in de vorm e=……
 vervang e in de vergelijking van de parabool door deze formule
3. vul de coördinaten van het tweede punt in de vergelijking van de parabool in je vindt nu
een waarde voor a
4. met de formule uit stap 2 kan je nu ook de waarde van e vinden
5. vul de gevonden waarden voor a, d en e in de algeme vergelijking van de parabool in
voorbeeld:
Bepaal de vergelijking van de parabool met als symmetrie-as x=4
en die door de punten (0,3) en (2,-9) gaat.
1. d = ……
de vergelijking van de parabool wordt:
2. vul (0,3) in de vergelijking van de parabool in:
 e=……
 de vergelijking van de parabool wordt:
3. vul (2,-9) in de vergelijking van de parabool in:
 a=……
4. e = …………… (zie stap 2)
5. de vergelijking van de parabool is:
Extra oefeningen: groene kopie REEKS 3 oefening 1
Hoofdstuk 1: Tweedegraadsfuncties
Derde soort oefeningen: het minimum of maximum zijn gekend
gebruik de tweede vorm van de vergelijking van de parabool y = ax²+bx+c
en zoek de waarde van a, b en c
1. meestal is a al gekend (gegeven in de opgave)
2. in de opgave staat: de functie bereikt een minimum (of maximum) voor x = … (een getal)
b
en vervang x door dit getal
2a

gebruik de formule x 




je vindt een formule waarin a en b staan
vorm deze formule om tot de vorm b=……
vervang in deze formule a door de waarde die je kent (uit de opgave)
je hebt nu de waarde van b gevonden: vervang in de vergelijking van de parabool
het symbool b door deze waarde
3. in de opgave staat: ‘dit minimum (of maximum) is …… (een getal)’ of: ‘de functie heeft een
minimum (of maximum) met …… (een getal) als functiewaarde’
 vervang in de vergelijking van de parabool y door dit getal en x door de waarde die
je ook in de opgave terug vindt
 je vindt op die manier de waarde van c
4. vervang a, b en c in de vergelijking y  ax²  bx  c door de gevonden waarden
voorbeeld:
Bepaal b en c zodat de functie y  3x²  bx  c een maximum bereikt
voor x = -2 en dat dit maximum 6 is.
1. a = …………
2. ‘de functie bereikt een maximum voor x = -2’
b
en vervang x door het gegeven getal:
2a

gebruik de formule x 

b = …………

de vergelijking van de parabool wordt:
3. ‘dit maximum is 6’

vervang in de vergelijking van de parabool y (of f(x)) door 6 en x door -2:

c = …………
4. vervang a, b en c in de vergelijking y  ax²  bx  c door de gevonden waarden:
Extra oefeningen: groene kopie REEKS 3 oefening 2
oefeningen in de klas: p.24 oefening 28(P1), oefening 29, oefening 30