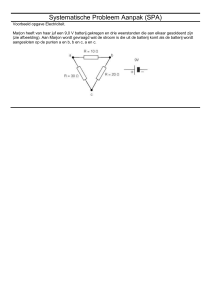
Gemengde schakelingen
Gemengde schakelingen
We hebben in vorige lessen de serieschakeling en de parallelschakeling behandeld. Veel schakelingen zijn een combinatie van de
serieschakeling en de parallelschakeling. Dat noemen we gemengde schakelingen.
Gemengde schakelingen zijn iets lastiger, want we moeten steeds kiezen of we de rekenregels van de serieschakeling gebruiken of de
rekenregels voor de paralelschakeling. In deze les leren we hoe je een gemengde schakeling kunt uitrekenen.
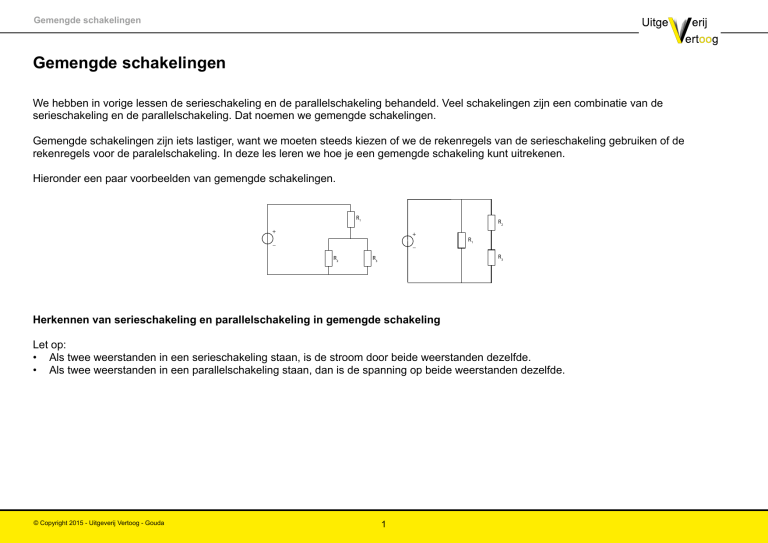
Hieronder een paar voorbeelden van gemengde schakelingen.
R1
R2
+
+
_
_
R2
R1
R3
R3
Herkennen van serieschakeling en parallelschakeling in gemengde schakeling
Let op:
• Als twee weerstanden in een serieschakeling staan, is de stroom door beide weerstanden dezelfde.
• Als twee weerstanden in een parallelschakeling staan, dan is de spanning op beide weerstanden dezelfde.
© Copyright 2015 - Uitgeverij Vertoog - Gouda
1
Gemengde schakelingen
We gaan nu eerst zoeken in onderstaande schakeling of er twee weerstanden zijn met dezelfde stroom. We zien dat R2 en R3 dezelfde stroom
hebben. Er is tenslotte geen enkel punt tussen R2 en R3 waar de stroom kan wegvloeien. De stroom door R1 is totaal anders, dus die staat niet
in dezelfde serieschakeling.
Er is in dit schema geen parallelschakeling te vinden. Er zijn geen twee weerstanden die dezelfde spanning hebben.
R2
+
R1
_
R3
Hoe pakken we het aan?
We kunnen nu eerst de serieschakeling uitrekenen. De twee weerstanden kunnen we dan vervangen door één Rtot23. Deze totale weerstand
vervangt dus de weerstanden R2 en R3. Als we dan een nieuw schema tekenen met R1 en Rtot23, dan zien we dat deze twee weerstanden parallel
staan. Nu kunnen we weer de rekenregels voor de parallelschakeling gebruiken en daarmee de Rverv uitrekenen.
Itot
Itot
I1
I2 3
I1
Itot
I2 3
R2
+
_
U
+
R1
_
U
R1
R3
© Copyright 2015 - Uitgeverij Vertoog - Gouda
2
Rtot 2 3
+
_
U
Rverv
Gemengde schakelingen
We gaan dat nog eens proberen. Nu met een ander schema. In het schema is te zien dat de weerstanden R1 en R2 parallel staan. Deze twee
weerstanden hebben dezelfde spanning. De stroom door R1 en R3 is niet dezelfde. En ook door R2 en R3 loopt niet dezelfde stroom. Er zit op dit
moment dus geen serieschakeling in het schema.
Itot
I1
I2
R1
R2
U1 2
+
Utot
_
R3
U3
Itot
De twee weerstanden R1 en R2 kunnen we vervangen door Rverv12. Als we dat gedaan hebben, hebben we een serieschakeling over van Rverv12
met R3. Van die serieschakeling kunnen we weer de totale weerstand Rtot uitrekenen.
Itot
Itot
U1 2
+
_
I1
I2
R1
R2
U1 2
+
Utot
_
U3
Itot
+
Utot
_
R3
U3
R3
Itot
Itot
© Copyright 2015 - Uitgeverij Vertoog - Gouda
Rverv 1 2
3
Utot
Rtot
Itot
Gemengde schakelingen
Oefenopgave 1
We gaan dat nu maar eens echt uitrekenen. We nemen het volgende schema. We weten de weerstanden en de spanning. We willen de
vervangingsweerstand weten van de gehele schakeling en we willen de stromen Itot, I1 en I2 weten.
Gegeven
R1 = 10 Ω
R2 = 4 Ω
R3 = 6 Ω
Utot = 20 V
Itot
I1
I2
R2 = 4 Ω
+
_
Utot = 20 V
R1 = 10 Ω
R3 = 6 Ω
Gevraagd
I1
I2
Rverv
Itot
Oplossing
Utot
I1 =
R1
20 V
I1 =
10 Ω
=2A
Om I2 te kunnen uitrekenen moeten we eerst van de serieschakeling van R2 en R3 de totale weerstand Rtot23 berekenen.
© Copyright 2015 - Uitgeverij Vertoog - Gouda
4
Gemengde schakelingen
Itot
Itot
I1
I2
I1
I2
R2 = 4 Ω
+
_
Utot = 20 V
+
R1 = 10 Ω
_
Utot = 20 V
R1 = 10 Ω
Rtot 2 3 = 10 Ω
R3 = 6 Ω
Rtot23 = R2 + R3
Rtot23 = 4 + 6 = 10 Ω
I2 =
I2 =
Utot
Rtot23
20
10
=2A
We hebben nu een parallelschakeling van R1 en Rtot23. We gaan nu de vervangingsweerstand Rverv uitrekenen.
1
=
Rverv
1
Rverv
Rverv
=
=
1
+
R1
1
10
10
2
+
1
Rtot23
1
10
=
2
10
=5
© Copyright 2015 - Uitgeverij Vertoog - Gouda
5
Gemengde schakelingen
De totale stroom kunnen we op twee manieren uitrekenen:
• We kunnen de stromen I1 en I2 optellen
• We kunnen de wet van Ohm gebruiken.
Eerst door het optellen van stromen:
Itot = I1 + I2
Itot = 2 A + 2 A = 4 A
Dan met de wet van Ohm:
U
tot
Itot =
Rverv
20 V
=4A
Itot =
5
Ω
© Copyright 2015 - Uitgeverij Vertoog - Gouda
6
Gemengde schakelingen
Oefenopgave 2
Nog maar eens zo’n opgave. We nemen het volgende schema. We weten de weerstanden en de spanning. We willen weten:
•
•
•
•
•
de vervangingsweerstand van de gehele schakeling
de stroom Itot
de spanning over R3
de spanning over R1
de stroom door R1
Itot
UR1
IR1
IR2
R1 = 12 Ω
R2 = 4 Ω
+
_
Utot = 32 V
R3 = 5 Ω
UR3
Gegeven
R1 = 12 Ω
R2 = 4 Ω
R3 = 5 Ω
Utot = 32 V
Gevraagd
Itot
UR3
UR1
IR1
© Copyright 2015 - Uitgeverij Vertoog - Gouda
7
Gemengde schakelingen
Oplossing
Om de totale stroom uit te rekenen moeten we de vervangingsweerstand van de gehele schakeling uitrekenen.
R1 en R2 zitten in een parallelschakeling. Die gaan we eerst uitrekenen
1
Rverv12
1
Rverv12
1
Rverv12
Rverv
=
=
=
=
1
R1
1
12
1
12
12
4
+
+
+
Itot
1
UR1
R2
_
R1 = 12 Ω
R2 = 4 Ω
Utot = 32 V
UR3
4
12
IR2
+
1
3
IR1
=
R3 = 5 Ω
4
12
= 3 Ω
Nu zit Rverv12 in serie met R3. We kunnen de totale weerstand van deze serieschakeling uitrekenen:
Rtot = Rverv12 + R2
Rtot = 3 + 5 = 8 Ω
De totale stroom kunnen we nu uitrekenen met de wet van Ohm:
Utot
Itot =
Rtot
32 V
Itot =
8Ω
=4A
© Copyright 2015 - Uitgeverij Vertoog - Gouda
8
Gemengde schakelingen
Deze totale stroom loopt door de batterij en door R3. De spanning over R3 is:
UR3 = Itot · R3
UR3 = 4 A · 5 Ω = 20 V
Itot = 4 A
Itot
UR1
IR1
IR2
R1 = 12 Ω
R2 = 4 Ω
UR1
+
_
+
Utot = 32 V
_
UR3
R3 = 5 Ω
Rverv 1 2 = 3 Ω
Utot = 32 V
UR3 = 20 V
R3 = 5 Ω
Als er van de 32 V van de batterij 20 V over R3 staat, dan is er nog maar 12 V over voor R1 en R2. R1 en R2 staan parallel, dus ze hebben beide
dezelfde spanning van 12 V.
Dus:
Utot = UR12 + UR3
UR12 = Utot – UR3
UR12 = 32 – 20 = 12 V
De stroom door R1 kunnen uitrekenen met de wet van Ohm. We weten de spanning over R1 en we wat de weerstand van R1 is
UR12
I1 =
R1
12 V
I1 =
12 Ω
=1A
Het is veel rekenwerk. Maar het is eigenlijk steeds weer dezelfde truc. Best lastig, maar als je het veel doet, wordt het vanzelf een stuk
makkelijker.
© Copyright 2015 - Uitgeverij Vertoog - Gouda
9