THEMA 4: bijzondere krachten

QUARK_6-Thema-04-bijzondere krachten
THEMA 4: bijzondere krachten
Blz.
1
QUARK_6-Thema-04-bijzondere krachten
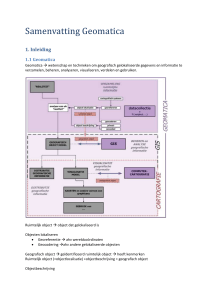
2dim.gevallen:
Componenten van positie-vector:
Blz.
Componenten van snelheids-vector
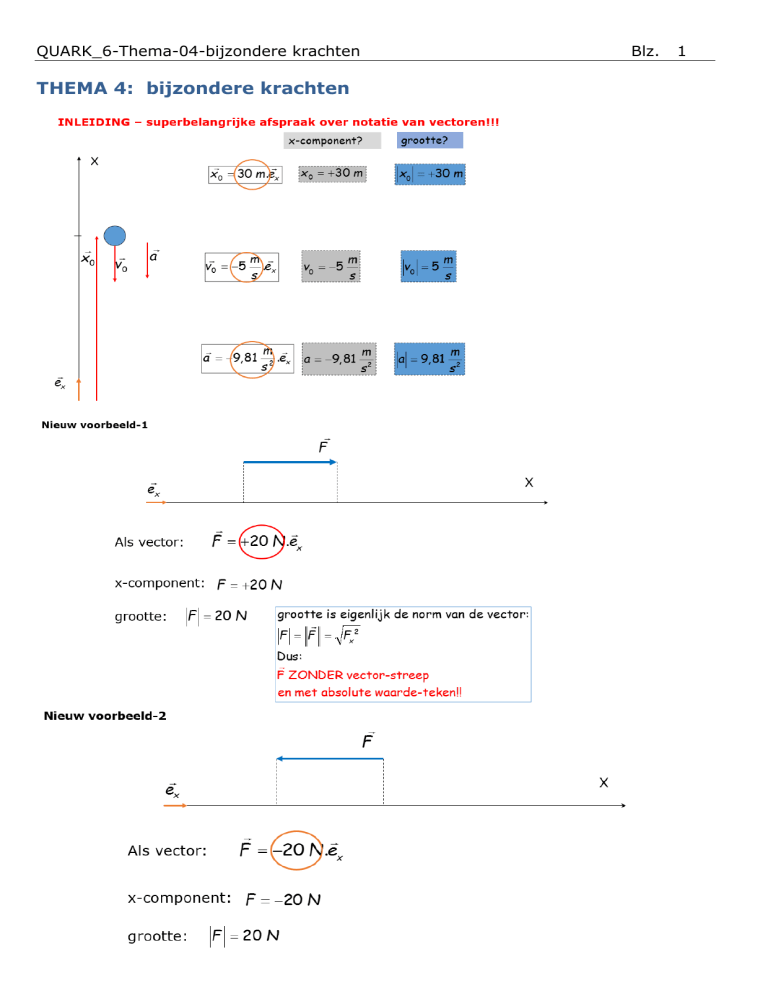
X
Normaalkracht
Een voorwerp dat ondersteund wordt, ondervindt vanwege het
steunvlak een normaalkracht Fn .
De normaalkracht staat steeds loodrecht op het steunvlak
Vectorvergelijking:
Projectie op X:
Fn + Fz = m.a
Fn − Fz = m.a x
2
QUARK_6-Thema-04-bijzondere krachten
Blz.
3
Wrijvingskracht
Proef:
Van (a) tot (d): statische wrijving
De statische wrijvingskracht heeft geen vaste waarde, maar wordt begrensd door een
maximale waarde. Hiervoor geldt: Fw , s max = µ s . Fn
µs is de statische wrijvingscoëfficiënt tussen twee oppervlakken.
Tijdens (e) en (f): dynamische wrijving
Voor de dynamische wrijvingskracht geldt: Fw ,d = µd . Fn
µd is de dynamische wrijvingscoëfficiënt tussen twee oppervlakken.
Er blijkt: µ s > µ d
BESLUIT:
Op een voorwerp in rust waarop een kracht F werkt evenwijdig met het
contactoppervlak met een ander voorwerp, werkt een statische wrijvingskracht
Fw,s die evenwijdig is met het contactoppervlak en tegengesteld aan F . Daarbij is
Fw,s < Fw ,s max = µ s . Fn
met
Fw,s max
de maximale statische wrijvingskracht en
Fn
de
normaalkracht.
Op een voorwerp dat over een oppervlak schuift, werkt een dynamische wrijvingskracht
Fw,d evenwijdig met het contactoppervlak en tegengesteld aan de zin van de
beweging, waarvoor geldt:
Fw ,d = µ d . Fn
QUARK_6-Thema-04-bijzondere krachten
Blz.
4
Spankracht
De grootte van de spankracht
Fs uitgeoefend door een gespannen touw of ketting op
een voorwerp, is gelijk aan de grootte van de kracht die door het touw wordt
doorgegeven. Daarbij wordt de massa van het touw verwaarloosd.
Fs = Fbt = Ftb = Fh
Er geldt:
De richting van de spankracht is die van het touw, de ketting, de staaf...
Intermezzo: verscheidene systemen kiezen (-> zie vb-opdracht ‘blokken op een rij’)
Zwaartekracht
Definitie
De aarde oefent op elk voorwerp met massa m een zwaartekracht uit:
Fz = m.g
Fz is gericht naar het middelpunt van de aarde. De grootte g van de
zwaarteveldsterkte of valversnelling is niet constant, maar verandert met de plaats op
aarde en neemt af met de hoogte boven het aardoppervlak.
In België is de gemiddelde waarde van g op het aardoppervlak gelijk aan 9,81 m/s2.
Zwaartepunt (L)
Gewicht
De kracht die de juffrouw op haar ondersteuning uitoefent, noemen we het
gewicht
Fg van de juffrouw.
Ze staat op een horizontale vloer en ze versnelt niet, daarom geldt:
Fg = Fz = Fn
BESLUIT:
Het gewicht Fg van een voorwerp is de kracht die dat voorwerp uitoefent op zijn
ondersteuning.
Deze kracht staat loodrecht op het contactoppervlak tussen het voorwerp en de
ondersteuning.
De normaalkracht
Fn is de reactiekracht op het gewicht Fg en Fg = Fn
Gewichtloosheid
Een voorwerp is gewichtloos als het geen kracht uitoefent op zijn ondersteuning.
1. Ruimtetuigen (-> L)
2. Paraboolvluchten (-> L)
QUARK_6-Thema-04-bijzondere krachten
Blz.
5
Gravitatiekracht
Definitie
Een puntmassa 1 met massa m1 oefent op een andere puntmassa 2 met massa m2
een aantrekkende gravitatiekracht
FG uit volgens de verbindingslijn tussen de
puntmassa’s. De grootte van die kracht is evenredig met m1 en m2 en omgekeerd
evenredig met het kwadraat van de afstand r tussen de puntmassa’s:
FG = G.
m1.m 2
r2
−11
Daarin is de gravitatieconstante G = 6,67.10
N.m2
kg2
Dat is de gravitatiewet.
De puntmassa 2 oefent op de puntmassa 1 een even grote aantrekkende gravitatiekracht
−FG uit.
Gravitatieversnelling
F = m.a ⇒ F = m. a 

mh
m
h =0
→
a = G. 2h
m.m h  ⇒ a = G.
2
en FG = G.
Rh
(Rh + h)
2 
R
+
h
( h ) 
De gravitatieversnelling op het aardoppervlak van de aarde noemen we de
valversnelling of zwaarteveldsterkte g .
Centripetale kracht
Op een voorwerp met massa m dat een cirkelvormige baan met cirkel R beschrijft met
een snelheid
v of een hoeksnelheid ω , werkt een centripetale kracht Fcp gericht
naar het middelpunt van de cirkel, met een grootte gelijk aan:
Fcp = m. a cp
met ω =
v2
= m. = m.ω2 .R
R
2π
= 2πf
T
QUARK_6-Thema-04-bijzondere krachten
Blz.
Satellietbanen
Voorbeeldopdrachten
Voorbeeldopdracht-1
Vectorvergelijking:
Fn + Fz = m.a
Projectie op X:
Fz .sin ( α ) = m.a x
Projectie op Y:
Fn − Fz .cos ( α ) = m.a y
⇒ ax =
Fz .sin ( α )
m
=
m.g.sin ( α )
m
= g.sin ( α )
6
QUARK_6-Thema-04-bijzondere krachten
Blz.
Voorbeeldopdracht-2
Voorbeeldopdracht-3
Vectorvergelijking:
Fn + Fz + FK + Fw,d = m.a
Projectie op X:
− Fw,d + FK .cos ( θ ) = m.a x
(1)
Projectie op Y:
Fn − Fz − FK .cos ( θ ) = m.a y
( 2)
Er geldt altijd : Fw,d = µ d. Fn ⇒ µ d =
Fw,d
Fn
We zoeken dus een uitdrukking voor de wrijvingskracht en de normaalkracht:
v = Ct ⇒ ax = 0 ⇒ Uit (1) : Fw,d = + FK .cos ( θ ) = 70, 7 N
v = Ct ⇒ ay = 0 ⇒ Uit (2 ) : Fn = Fz + FK .cos ( θ ) = 267 N
Besluit : µd =
Fw,d
Fn
=
70,7 N
= 0,265
267 N
7
QUARK_6-Thema-04-bijzondere krachten
Blz.
8
Voorbeeldopdracht-4
Vectorvergelijking:
Fn + Fz + Fw,d = m.a
(1)
Projectie op X:
− Fw,d = m.a x
Projectie op Y:
Fn − m.g = m.a y = 0 ( 2 )
Uit (1) ⇒ Fw,d = −m.ax
Uit (2 ) ⇒ Fn = m.g
(1')
(2 ')
Er geldt altijd : Fw,d = µd. Fn ,
dus via (1') en (2 ') : − m.ax = µd.m.g
⇔ ax = −µd.g = −0, 80.9, 81
m
m
≈ −7, 8 2
2
s
s
Voorbeeldopdracht-5
Vectorvergelijking:
Fn + Fz + Fs = m.a = 0
Projectie op X:
Fs − Fz .sin θ = 0
(1)
Projectie op Y:
Fn − Fz .cos θ = 0
( 2)
Uit (1) ⇒ Fs = Fz .sin θ = 98 N
Uit (2 ) ⇒ Fn = m.g.cos θ = 17.101 N
Extra-voorbeeldopdracht: blokken ‘op een rij’
Twee massa’s van 5,0 kg en 10,0 kg zijn met elkaar in contact. De blokken liggen op
een tafel en kunnen wrijvingsloos bewegen. Een uitwendige kracht van 30,0 N duwt
de massa’s naar links.
Zoek de versnelling van elk van die blokken.
Zoek de duwkracht P21 die het grote blok-2 uitoefent op het kleine blok-1.
QUARK_6-Thema-04-bijzondere krachten
Blz.
9
Extra-voorbeeldopdracht: inzicht over 3 blokken
Drie massa’s van 1,0 kg zijn met elkaar in contact via een touw. De blokken liggen op
een tafel en kunnen wrijvingsloos bewegen. Een uitwendige kracht van 30,0 N trekt
de massa’s naar rechts. Zoek de versnelling en netto-krachten op elk van die blokken.
We gaan nu even ‘kort door de bocht’ en proberen eens zonder het strakke stramien
van de vectorvergelijkingen. We doen dit om je inzicht te vergroten in de fysica achter
de situatie.
Extra-voorbeeldopdracht: dan toch maar eens Newton…
Twee massa’s van 2 kg en 6 kg zijn met elkaar verbonden via een touw. De blokken
liggen op een tafel en kunnen wrijvingsloos bewegen. Een uitwendige kracht van 15 N
trekt de massa’s naar rechts. Zoek de versnelling van elk van die blokken. Zoek ook
de spankracht die in het touw tussen de blokken heerst.
QUARK_6-Thema-04-bijzondere krachten
Blz.
Voorbeeldopdracht-6
Aap als systeem:
Vectorvergelijking:
Projectie op Y:
Fs1 + Fza = ma .a a
Fs1 − Fza = m a .a a
(1)
Banaan als systeem:
Vectorvergelijking:
ab
Projectie op Y:
aa
Fs2 + Fzb = mb .a b
Fs 2 − Fzb = m b .a b
( 2)
Dus:
Uit ( 2 ) : Fs2 = m b .a b + Fzb = m b .a b + m b .g ( 2 ')
en uit (1) : Fs1 = m a .a a + Fza = m a .a a + m a .g (1')
De versnellingen zijn even groot maar tegengesteld:
a b = −a a
De spankrachten zijn even groot en hebben dezelfde zin:
Fs1 = Fs2
Dus via (1') en ( 2 ') : m b .a b + m b .g = ma .a a + ma .g
en met a b = −a a : −m b .a a + m b .g = ma .a a + ma .g ⇒ a a =
m b .g − ma .g
m
≈ −2,1 2 ⇒ Fs1 = ...
m b + ma .
s
Voorbeeldopdracht-7
van 0 → 1: a = 2, 00
van 1 → 2 : a = 0
m
s2
(versnelling)
m
s2
(vertraging)
m
s2
van 2 → 4 : a = 1, 00
Oplossing:
Vectorvergelijking: Fn + Fz = m.a
(
Projectie op Y: Fn − Fz = m.a y ⇒ Fn = m. g + a y
van 0 → 1: a = 2, 00
) (1)
m
⇒ (1) wordt : Fn = m. ( g + a ) = 945 N
s2
m
⇒ (1) wordt : Fn = m. ( g ) = 785 N
s2
m
van 2 → 4 : a = 1 2 ⇒ (1) wordt : Fn = m. ( g − a ) = 705 N
s
van 1 → 2 : a = 0
10
QUARK_6-Thema-04-bijzondere krachten
Blz.
11
Voorbeeldopdracht-8
Vectorvergelijking: FL = m.a
Projectie op Y: FL = m. a
(1)
Nu is FL = B . Q . v
v2
R
2
mv
v
Dit vervangen we in (1) : B . Q . v = m.
⇒R=
B.Q
R
en we weten dat FL een cp-werking heeft ⇒ a = ω2 .R =
Voorbeeldopdracht-9
Vectorvergelijking: Fs + Fz = m.a
Projectie op X: Fs .sin θ = m.a x
(1)
Projectie op Y: Fs .cos θ − Fz = m.a y = 0
(1) wordt :
Fs .sin θ = m. a
(2)
(1' )
We kunnen we ( 2 ') schrijven als : Fs . cos θ = mg
mg
( 2 '')
cos θ
We weten ook dat FL een cp-werking heeft ⇒ a = ω2 .R
⇒ Fs =
Dit vervangen we in (1') samen met ( 2") :
mg .sin θ = m.ω .R
2
cos θ
( 2π ) .R.cos θ
g
 2π 
.sin θ =   .R ⇔ T 2 =

→
cos θ
 T 
g.sin θ
ω=
2π
T
L=
R
sin θ
→ T = ( 2π )
2
2
L cos θ
g
Voorbeeldopdracht-10
In het hoogste punt:
Vectorvergelijking: FnA + Fz = m.a
a cp
(1)
Projectie op Y: − FnA − Fz = m.a y
− FnA − Fz = − m. a ⇔ FnA + Fz = m. a
v2
We weten ook dat FL een cp-werking heeft ⇒ a = ω .R =
R
2
2
v
v
Dus : FnA + m.g = m. ⇒ FnA = m − mg ≈ 1,93.104 N
R
R
In het laagste punt:
2
Vectorvergelijking: FnB + Fz = m.a
Projectie op Y: FnB − Fz = m.a y
FnB − Fz = m. a ⇔ FnB = m. a + Fz
(1)
a cp
QUARK_6-Thema-04-bijzondere krachten
Blz.
We weten ook dat FL een cp-werking heeft ⇒ a = ω2 .R =
Dus : FnB = m.
v2
R
v2
+ m.g ≈ 26,3.10 4 N
R
Voorbeeldopdracht-11
In het hoogste punt:
a cp
Vectorvergelijking: Fn + Fz = m.a
Projectie op X: − Fn + Fz = m.a x
(1)
⇔ Fn = Fz − m. a
v2
We weten ook dat FL een cp-werking heeft ⇒ a = ω .R =
R
2
Dus : Fn = m.g − m.ω2 .R ⇒ valversnelling op evenaar : g ' = g − ω2 .R ≈ 9, 77
m
s2
12