Flowlabpracticum Samenvatting Lynn Verkroost, Nick

Flowlabpracticum - Lynn Verkroost, Nick Van Bossche en Michiel Haegeman
Vleugelprofiel
Drukcoëfficiënt
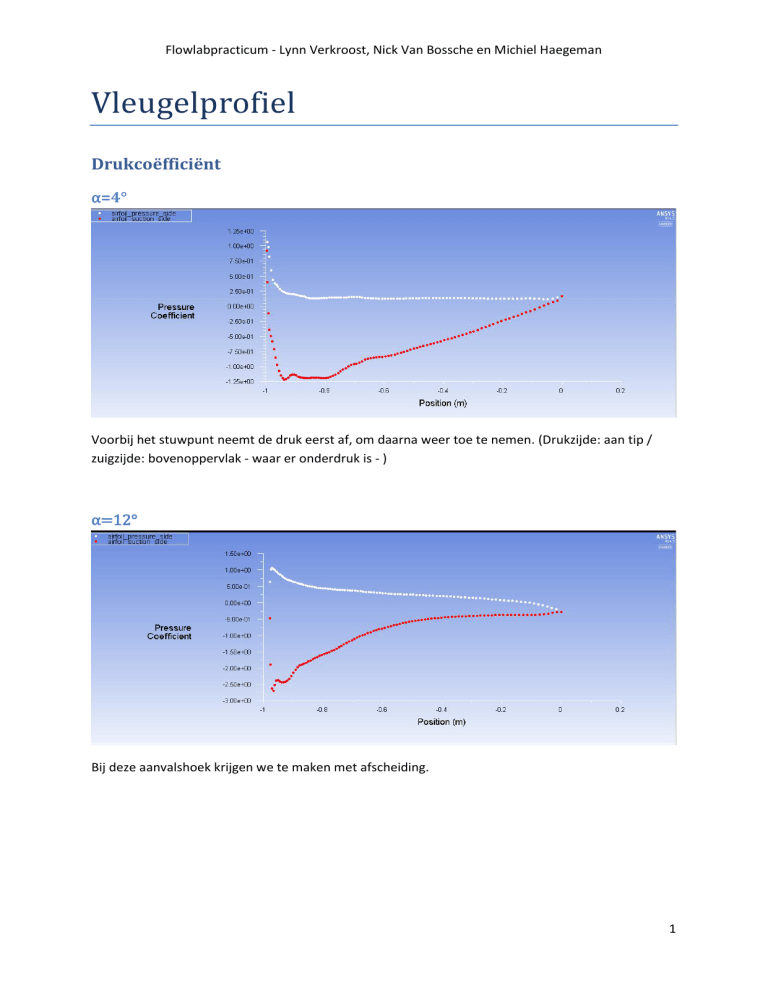
α=4°
Voorbij het stuwpunt neemt de druk eerst af, om daarna weer toe te nemen. (Drukzijde: aan tip /
zuigzijde: bovenoppervlak - waar er onderdruk is - )
α=12°
Bij deze aanvalshoek krijgen we te maken met afscheiding.
1
Flowlabpracticum - Lynn Verkroost, Nick Van Bossche en Michiel Haegeman
Lift- en weerstandsverloop
CL, CD
Voor grote α neemt CD toe, maar neemt CL af (want er is geen onderdruk meer). Het is dus niet zinvol
om de aanvalshoek te blijven vergroten. Het is wel zinvol om de verhouding CL/CD te optimaliseren.
Liftcoëfficiënt:
Hoe groter de draaiing tot op een bepaald niveau, hoe meer lift.
Waarom? Profiel is gedraaid. De lucht volgt mooi je profiel. Hierdoor is er ook een impuls in
de y-richting (negatieve zin). -> Actie = reactie -> Er is een lift naar boven om evenwicht te
behouden. Vanaf een bepaalde hoek (bv. 16°) zal je stroming niet meer mooi je profiel
volgen. (Bv. vleugel 90° gedraaid dan zal stroming inderdaad profiel niet meer mooi volgen.)
Hierdoor zal impuls dus minder zijn en zal je dus een lagere lift hebben.
Weerstandkracht:
Hoe meer je profiel gedraaid is, hoe meer weerstand.
Invloed van de aanvalshoek
Druk
α =4°
2
Flowlabpracticum - Lynn Verkroost, Nick Van Bossche en Michiel Haegeman
Aan de bovenkant van het vleugelprofiel is de druk het laagst (zuigzijde).
In het drukverloop zie je geen zog, want
. De druk verandert immers langs het profiel, niet er
dwars over.
α =12°
Het stuwpunt bevindt zich aan de drukzijde, een beetje voorbij de aanvalsboord. Indien dit niet het
geval zou zijn, zouden we in de grafiek van de drukcoëfficiënt de hoogste druk al moeten vinden voor
positie -1.
Snelheid
Voor lage snelheden (geen stromingsverliezen, visceuze termen verwaarloosbaar) geeft de wet van
Bernoulli het verband tussen snelheid en druk.
Op een stroomlijn die uit de buurt van de grenslaag blijft, mag Bernoulli dus toegepast worden.
Doorheen de grenslaag mag Bernoulli echter niet toegepast worden.
α =4°
Aan het stuwpunt is de snelheid laag.
De hoogste snelheid vind je aan de zuigzijde, want daar is de druk het laagst.
In de zogzone is de snelheid weer lager. Door viscositeit en impuls neemt de snelheid echter weer
toe.
3
Flowlabpracticum - Lynn Verkroost, Nick Van Bossche en Michiel Haegeman
α =12°
De grenslaag is dikker.
Hier krijgen we te maken met afscheiding.
Temperatuur
=
α =4°
4
Flowlabpracticum - Lynn Verkroost, Nick Van Bossche en Michiel Haegeman
De temperatuur stijgt aan het stuwpunt (door compressie, zie bij α=12°).
Ook in het zog stijgt de temperatuur, door dissipatie in de grenslaag (dit zie je niet in het
drukverloop).
Daarna neemt de temperatuur weer af. Dit is geen gevolg meer van de drukgradiënt of van dissipatie,
maar wel van de term
. Dit wil zeggen dat de temperatuur afneemt door conductie, omdat
boven en onder de warme zone de temperatuur lager is.
Een fluïdumdeeltje warmt op in de grenslaag.
Op tip: alle deeltjes worden op elkaar gedrukt, wat zorgt voor een hoge druk en dus voor
een hoge temperatuur.
Op het bovenvlak zien we een grote blauwe vlek. We hebben daar (doordat de deeltjes naar
boven worden gestuurd) een onderdruk. Dit staat gelijk met een lagere temperatuur. Op de
rand zelf zien we een hogere temperatuur. Dit komt door de wrijving van de luchtdeeltjes op
het oppervlak. Meer naar het einde toe wordt deze hogere temperatuurrand dikker en
dikker omdat men reeds veel wrijving heeft ondergaan. Wanneer men het vleugelprofiel
voorbij is, kan het door convectie beginnen afkoelen. Je ziet dat dit gebeurt. De omgevende
lucht is kouder dan de lucht die komt van de vleugel, dus is er een warmteoverdracht van
warm naar koud.
α =12°
Als je een stroomlijn volgt, neemt de temperatuur eerst af, om dan weer toe te nemen. (Daarna
komt afscheiding.) Dit heeft te maken met compressie (T en p stijgen) en expansie (T en p dalen) van
de fluïdumdeeltjes.
Aan het stuwpunt is er compressie: p en T stijgen.
In de zogzone heerst een hogere temperatuur, want de warmte van de deeltjes die door dissipatie
een hogere temperatuur hebben, wordt door afscheiding mee getransporteerd naar de zogzone. (Op
het einde van het vleugelprofiel zijn alle gradiënten en snelheden klein, en zijn de afstanden groot.
Hier vindt dus geen dissipatie meer plaats. De deeltjes waren dus al warm voor ze hier aankwamen.)
5
Flowlabpracticum - Lynn Verkroost, Nick Van Bossche en Michiel Haegeman
Machgetal
De (geluids)snelheid is een functie van de temperatuur en kan dus van punt tot punt veranderen.
M=0.3
Maximum = 0.44
Verloop M snelheidsverloop
M=0.8
Druk
Snelheid (Mach)
6
Flowlabpracticum - Lynn Verkroost, Nick Van Bossche en Michiel Haegeman
Vectorsnelheid
Aan de zuigzijde neemt het Machgetal toe.
De zone waar onderdruk heerst versnelt, waardoor het Machgetal 1 bereikt. In de divergente zone
stijgt de snelheid nog verder, omdat we nu met supersone snelheden werken.
Dus: normaal daalt de snelheid in het divergent, maar bij supersone snelheden stijgt de snelheid ook
in het divergent.
Er moet weer een overgang zijn van supersone naar subsone stroming. Dit gebeurt over een afstand
van enkele micrometers: een schokgolf. (In het echt is deze schokgolf dus haarfijn, maar door het
rekenrooster werd ze hier uitgesmeerd.)
M=1.3
De aankomende stroming is supersoon.
De schokgolf voor het profiel noemen we een boeggolf (cfr. schip).
7
Flowlabpracticum - Lynn Verkroost, Nick Van Bossche en Michiel Haegeman
Druk
Snelheid
M=2.0
Druk
Blauw: atmosfeerdruk
8
Flowlabpracticum - Lynn Verkroost, Nick Van Bossche en Michiel Haegeman
Snelheid (Mach)
Vectorplot snelheid (12° - al de rest (bovenstaande) is over 4° gedraaid)
Het effect is hier sterker dan bij M=1.3.
Aan het profiel moet de snelheid 0 zijn. Dit veroorzaakt de schokgolf.
9
Flowlabpracticum - Lynn Verkroost, Nick Van Bossche en Michiel Haegeman
Temperatuur
Druk
Snelheid
Intermezzo: raket
Waarom neemt de snelheid toe als de dwarsdoorsnede groter wordt? Dit lijkt toch niet in
overeenstemming met de wet van massabehoud ( =
)?
=
Bij supersone stroming:
M>1
 als A 
v
 ρ 
gas wordt ijl
10
Flowlabpracticum - Lynn Verkroost, Nick Van Bossche en Michiel Haegeman
Dit is dus niet in tegenspraak met de wet van massabehoud.
Dit kan wel enkel voor een compressibel fluïdum, zoals een gas.
Invloed van Machgetal
Wanneer CD daalt, blijft de weerstand D wel toenemen (want V∞ blijft toenemen).
M=0.3
De drukveranderingen spelen zich enkel af op kleine afstand van het profiel.
M=0.8
De schokgolf staat bijna loodrecht.
Wanneer de schokgolf zich verplaatst, krijg je plots andere krachten op je structuur. Hierdoor kan
deze sterk gaan trillen (hiermee moet je rekening houden in het ontwerp). Bovendien heb je veel
stuwkracht nodig, want D stijgt gigantisch.
De drukveranderingen blijven nog steeds lokaal.
11
Flowlabpracticum - Lynn Verkroost, Nick Van Bossche en Michiel Haegeman
M=1.3
De schokgolf verplaatst zich naar achter en wordt schuiner en schuiner.
De drukveranderingen (supersoon, boeggolf) zijn waarneembaar over grote afstand.
M=2.0
De stroming is stabiel.
Je hoort 2 knallen wanneer de schokgolven je bereiken.
Je hoort steeds een knal wanneer het vliegtuig supersoon vliegt (dus niet enkel bij het breken van de
geluidsmuur).
=2
drukgolf van
1
1 Pa  100 dB
10 Pa  120 dB
Je hoort dus wel degelijk luide knallen, zelfs al vliegt het vliegtuig zeer hoog.
12
Flowlabpracticum - Lynn Verkroost, Nick Van Bossche en Michiel Haegeman
Temperatuursinvloed
Door de luchtvochtigheid vormt er zich een wolk in de omgeving van het vliegtuig.
Wanneer de temperatuur daalt, treedt er immers condensatie op, waardoor deze wolk ontstaat.
bij Mach=0.8:
Aan het stuwpunt stijgt de temperatuur. Dan stijgt het Machgetal , de druk daalt, er treedt expansie
op en de temperatuur daalt. Hierdoor treedt condensatie op.
Bij de schokgolf is er weer een plotse temperatuurstijging, waardoor er verdamping optreedt en de
wolk weer verdwijnt.
13
Flowlabpracticum - Lynn Verkroost, Nick Van Bossche en Michiel Haegeman
Rechthoekige plaat
Snelheidsgrenslaag op het einde van de plaat
Voor ReL = 100 000 is er meer wrijving dan voor ReL = 10 000.
Voor ReL = 1E7 (turbulente stroming) is er veel meer impulsoverdracht op de grenslaag.
(Het rooster is eigenlijk niet fijn genoeg.)
Heel dicht bij de wand is de turbulentie weg.
Voor ReL = 1E7 heb je de grootste wrijvingscoëfficiënten en de grootste wrijvingsweerstand, maar
hier heb je wel weinig weerstand ten gevolge van drukkrachten.
Dikte van de grenslaag
ReL = 10 000, Pr = 1
Temperatuur
14
Flowlabpracticum - Lynn Verkroost, Nick Van Bossche en Michiel Haegeman
Snelheid

groot
 meer wrijving

klein
 minder wrijving
oranje lijn volgens
Wanneer Pr = 1 zijn de temperatuurs- en snelheidsgrenslaag even dik (zie PPT H12-19-20, slide 12).
De dikte van de grenslaag daalt wanneer ReL stijgt.
Hoe dunner de grenslaag (en dus hoe hoger ReL), hoe groter de gradiënt en hoe beter de
warmteoverdracht.
Op einde: kleinere temperatuursgradiënt. Temperatuursverloop op grotere afstand -> lagere grad.
15
Flowlabpracticum - Lynn Verkroost, Nick Van Bossche en Michiel Haegeman
Lokale convectiecoëfficiënt
Hoe dikker de grenslaag, hoe slechter de warmteoverdracht, want
=
.
Vooraan: grenslaag oneindig dun. Stilaan wordt grenslaag dikker. Temperatuursgradiënt
wordt groter als grenslaag dun is. Aan de wand zelf is er enkel conductie. Er is meer
warmteoverdracht voor een dunnere grenslaag (Want voor conductie: q/a = -k* grad(T) en
we stelden net dat de gradiënt meer stijgt naarmate de grenslaag in dikte daalt ) . Zelfde
temperatuur voor grotere afstand -> temperatuursgradiënt kleiner
16
Flowlabpracticum - Lynn Verkroost, Nick Van Bossche en Michiel Haegeman
ReL = 10 000, Pr = 100
Temperatuurgrenslaag
Snelheidsgrenslaag
De snelheidsgrenslaag is nu dikker dan de temperatuursgrenslaag.
Voor grotere Pr-getallen is de temperatuursgrenslaag dunner en dus is de warmteoverdracht dan
17
Flowlabpracticum - Lynn Verkroost, Nick Van Bossche en Michiel Haegeman
beter.
((Synthetische) olie heeft een hoger Pr-getal dan water, dus kan je met dezelfde geometrie een
betere warmteoverdracht - en dus een betere koeling - krijgen met olie dan met water.)
Re = 100 000, PR = 1
Thermische grenslaag:
Snelheidsgrenslaag
Verband tussen Nusselt, Reynolds en Prandtl
De gevonden formule geldt enkel bij laminaire stroming!
3. Berekeningen
a) Q=665.8 (via report-fluxes-wand….)
rho=1
Cp=1000
18
Flowlabpracticum - Lynn Verkroost, Nick Van Bossche en Michiel Haegeman
k=0.1
µ=0.0001
Nu=66.5832
b) Rho aanpassen naar 10
Q=2098
Nu=209.8
c) Cp=1000000
Q=3121.908
Nu=312.19
Stelsel van drie vgl en drie onbekenden -> Maple
Een turbulente grenslaag (ReL = 1E7, Pr = 1)
Hier is er veel meer wrijving dan bij ReL = 10 000.
De dikte van de grenslaag is ongeveer gelijk.
Er is bijna geen temperatuursvariatie, behalve heel dicht bij de wand. Daar is er een zeer grote
temperatuursgradiënt en is er dus ook goede warmteoverdracht.
Wanneer we Nu voorspellen mbv de laminaire formule, krijgen we NuL = 2083.9.
In werkelijkheid geldt NuL = 15 434.3.
Het gebruik van de laminaire formule in de turbulente grenslaag zorgt dus voor een zware
onderschatting!
Conclusie: voor een goede warmteoverdracht heb je turbulente stroming en grote Pr-getallen nodig.
19
Flowlabpracticum - Lynn Verkroost, Nick Van Bossche en Michiel Haegeman
Je ziet hier een héél dun laagje. Dit wijst op een hoge snelheidsgradiënt, wat te verwachten
is bij turbulente stroming. De grenslaag stijgt, maar dit is heel moeilijk te zien.
Hier zie je dat in het begin de snelheid héél sterk stijgt (in vergelijking met laminaire
stroming). Dit wijst op het turbulent karakter.
Turbulente stroming is een goede menger. Dit zal ervoor zorgen dat er kouder water van
boven meer tot bij de wand komt en warmer water van de wand meer naar boven gaat.
Hierdoor wordt de temperatuurgradiënt groter en dus de warmteoverdracht groter (q/A = k*grad(T) ). Turbulente stroming is dus belangrijk voor een goede warmteoverdracht.
Dit kan je ook zien op de onderstaande plots. Je zien dat de snelheidsgradiënt veel hoger ligt
(dunner laagje),...
20