Vraagstuk 1

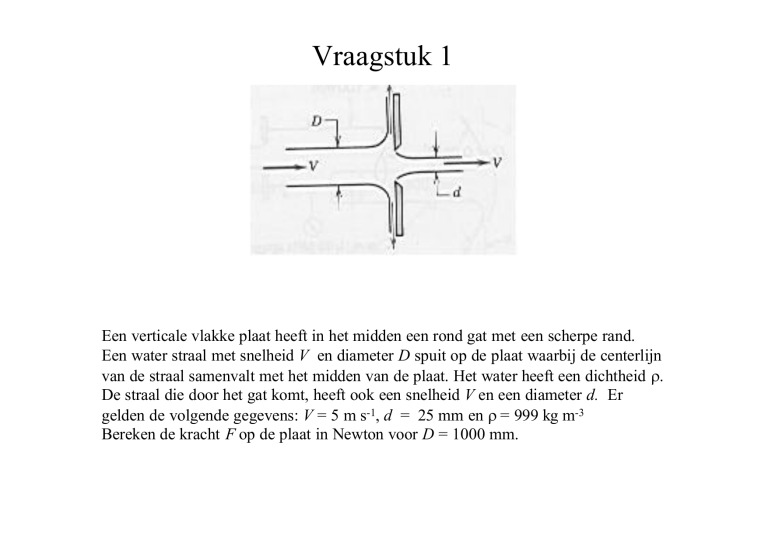
Vraagstuk 1
Een verticale vlakke plaat heeft in het midden een rond gat met een scherpe rand.
Een water straal met snelheid V en diameter D spuit op de plaat waarbij de centerlijn
van de straal samenvalt met het midden van de plaat. Het water heeft een dichtheid ρ.
De straal die door het gat komt, heeft ook een snelheid V en een diameter d. Er
gelden de volgende gegevens: V = 5 m s-1, d = 25 mm en ρ = 999 kg m-3
Bereken de kracht F op de plaat in Newton voor D = 1000 mm.
Vraagstuk 2
Een vloeistof met dichtheid
ρ = 891 kg/m3 stroomt door een ronde
buis met een bocht met diameters
D1=2R1=10 cm en D2 =2R2 = 6 cm.
Het vloeistofdebiet door de buis is
Q= 0.04 m3/s.
Bereken de y-component van de kracht in Newton op de buis alleen tengevolge van
impuls (de bijdrage van de druk mag verwaarloosd worden) voor:
a: een uniform snelheidsprofiel in doorsnede 1 en 2
b: in doorsnede 1:V1 ( r ) = V1
(1 − r 2 / R12 ) en in doorsnede 2: V2 ( r ) = V2
(1 − r / R2 )
1/7
waarin de r de radiele coördinaat is ten opzichte van de centerlijn van de buis.
De V2 en V1 zijn twee snelheden die volgen uit Q door toepassen van de definitie
van behoud van massa in doorsnede 1 en 2
Vraagstuk 3
De naald van een injectiespuit heeft
een binnendiameter van d = 0.1 mm
en een lengte van L = 25 mm.
We veronderstellen dat de kracht
die op de zuiger van de injectiespuit
wordt uitgeoefend gelijk is aan F =
45 N. De diameter van de zuiger is
D = 10 mm. We mogen
veronderstellen dat de stroming in
de injectienaald overal volledig
ontwikkeld is.
Bepaal het volume debiet Q in mm3 s-1 voor een vloeistof met µ = 5 10-3 kg m-1 s-1
(wrijving is alleen van belang in de naald en niet in de cylinder.)
Vraagstuk 4
Beschouw een horizontale plaat met een
halve breedte gelijk aan L (loodrecht op
F
het vlak van de tekening mag de plaat
V
oneindig lang genomen worden). De plaat
L
L
beweegt met een constante snelheid V=
p
0.5 m s-1 naar een vaste wand. Tussen de p0
0
plaat en de wand bevindt zich overal een
y
u
h
x
vloeistof met een dynamische viscositeit
µ = 5 10-3 kg m-1 s-1. Ter weerszijde van
en boven de plaat is de druk gelijk aan p0. De afstand tussen de plaat en de wand
bedraagt h = 5 mm
Bepaal de kracht F per meter (loodrecht op het vlak van de tekening) in kN m-1
die nodig is voor een plaat met L = 0.25 m.
Vraagstuk 5
De natuurlijke trillingsfrequentie van een massa
M geplaatst op een staaf met een lengte L en een
cirkelvormige doorsnede d is gelijk aan ω . De
stijfheid van de staaf is EI. Een proef met M = 3. x kg,
op een staaf van staal met L = 0.4 m, en een diameter
d = 12 mm levert voor de natuurlijke frequentie een
waarde op ω = 0.9 Hz.
Gebruik deze gegevens om de natuurlijke frequentie
te bepalen van een staaf met dezelfde afmetingen maar
gemaakt van aluminium en met een massa M = 2 kg
Verder geldt Estaal = 2.03 1011 Pa, Ealuminium = 7.4 1010 Pa
Vraagstuk 6
Door een buis met diameter D = 150 mm
stroomt water. De waterhoogte in de eerste
meetbuis is gelijk aan h = 1.6 m. De ruwheid
van de pijp e = 0.046 mm. Bereken het
volumedebiet van de vloeistof dat door de buis
stroomt. De zwaartekrachtsversnelling is g =
9.81 m s-2.
Verder is gegeven dat ν= 0.113 10-5 m2/s.
Vraagstuk 7
In het hiernaast geschetste systeem zijn
de lengten van de verschillende pijpen
gelijk aan: 75 m met een diameter van
20 cm , 150 m met 60-cm diameter en
100 m met 30 cm diameter. De
uitstroom ligt op een niveau van 0 m.
Voor de verliescoëfficiënten van elk van
de bochten geldt K = 0.95, van de klep
K = 6.3, van de plotselinge verwijding
K = 0.79 en van de inloop K = 0.5.
Bereken het maximale vermogen P in
kWatt dat de turbine kan leveren als het
water niveau gelijk is aan h = 50 m.
Verder is gegeven ρ = 1000 kg/m3, ν = 1.13 10-6 m2/s, e= 0.46 mm
voor alle pijpen en g=9.81 m/s2
Vraagstuk 8
Beschouw een T-stuk zoals hiernaast geschetst. De
Kk L
L2
2
-1
instroomsnelheid V = 3.0 m s . De lengte en diameter
p0
V
l
van de instroompijp zijn L1 = 2 m en D1 = 0.1 m. De
p0
Vr
druk in de instroom opening is p1 = 50 kPa. De twee
D2
zijtakken hebben een lengte van L2 = 4 m en diameter
Kb
van D2 = 0.08 m. De druk aan beide uitstroom
L1
D
1
openingen is p0. In de linker zijtak bevindt zich een
p1
klep die in geopende toestand een verliesfactor van
Kk= 5.0 introduceert. De rechte bocht plus
V
vernauwing heeft een verliesfactor van
Kb =1.0 betrokken op V. De ruwheid van alle pijpen is e = 0.1 mm. Voor de
berekening van de frictiefactor f moet de formule van Colebrook gebruikt worden.
De dichtheid is ρ = 999 kg m-3 en de viscoiteit µ = 0.001 Pa s.
a: Bereken de druk p0 in kPa voor het geval dat de klep dicht is dus V1=0.
b: Bereken de druk p0 in kPa voor het geval dat de klep open is (deze vraag is
moeilijk en vergt de oplossing van een set niet-lineare vergelijkingen met de
computer!).
Vraagstuk 9
Beschouw een laminaire grenslaag
met een snelheidsprofiel
 y  y p
u = U 2 −   
 δ  δ  
waar U = constant de snelheid buiten de
grenslaag is en de exponent p = 2.0.
Met de impulsbalans voor de grenslaag volgt voor de wrijvingscoëfficiënt
cf =
Bereken de constante C
C
Ux
ν
Vraagstuk 10
L
Lucht bij standaardcondities stroomt over een
dunne vlakke plaat van L=1.0 m lang en
b=0.3 m breed. De stroming is uniform aan de
voorrand van de plaat. Veronderstel dat het
snelheidsprofiel lineair is in de grenslaag. De
snelheid buiten de grenslaag is: U = 2.7 m/s. Op
de afstand L van de voorrand is de grenslaaghoogte δ = 8 mm. Beschouw de stroming als
twee-dimensionaal.
a: bereken met het controlevolume abcd de massastroom m& a b in g/s over het vlak ab
b: Bepaal de kracht F in mN die nodig is om de plaat op zijn plaats te houden
Voor lucht bij standaardcondities geldt voor de dichtheid ρ = 1.23 kg/m3
Vraagstuk 11
Een racewagen heeft met een gewicht van W = 12000 N en een
weerstandscoëfficiënt Cd = 0.4 betrokken op het frontaal oppervlak A = 2.3 m2.
De wagen versnelt van 0 tot V = 100 km uur-1 door middel van een constant
koppel op alle vier de wielen gelijk aan T = 1200 N m. De diameter van de
banden is D = 0.6 m.
De luchtdichtheid is ρ = 1.23 kg m-1 en de versnelling van de
zwaartekracht is g=9.81 m s-2.
Bereken de tijd waarin de snelheid V bereikt wordt
Vraagstuk 12
Een vleugelprofiel met een koorde c = 2 m staat onder een invalshoek α = 10 ° in
een horizontale stroming met snelheid U = 75 m s-1. De weerstandscoefficient
CD= 0.5 en de liftcoefficient is C L = 2π sin α. De luchtdichtheid is ρ = 1.23 kg m-1
Bereken de hoek θ (in graden) die de resulterende kracht op het vleugelprofiel
maakt met de horizontaal
Vraagstuk 13
Voor een vliegtuig dat met supersone snelheid vliegt, zijn de lift- en weerstandscoëfficiënt alleen een functie van het Mach getal:
CL= CL(M) en CD= CD(M)
Waarbij de CL en CD zijn betrokken op het oppervlakte van de vleugel dat een
spanwijdte van b = 75m een een koorde c = 5m heeft. Het vliegtuig vliegt met een
snelheid van V = 780 m/s en met een waarde van CD = 0.1 op een hoogte van 20km.
Op deze hoogte is de temperatuur gelijk aan T = 216.7 K. De prestaties van het
vliegtuig worden gemeten in een supersone windtunnel met een schaalmodel van 1
op 10. De wind-tunnel wordt gevoed uit een groot reservoir met gecomprimeerde
verwarmde lucht. De reservoir temperatuur TW = 527 °C= 800 °K en een reservoir
druk pw = 106 Pa . De stroming in de windtunnel kan als verliesvrij beschouwd
worden.
Wat is de weerstand FD van het model in kN?
Voor lucht geldt R = 286 Nm/(kgK) en κ=1.4
Vraagstuk 14
Door een convergent-divergent kanaal stroomt lucht vanuit een vat naar de
atmosfeer met een druk pa = 101 kPa. Het vat heeft een inhoud van I = 40 m3 en de
uitstroomopening van het kanaal heeft een oppervlak van Ae = 10 cm2. Bij het begin
van de stroming is de druk in het vat p0 = 800 kPa en de temperatuur T0 = 373 K.
De stroming mag als isentroop beschouwd worden.
De gasconstante voor lucht is R = 287 m2 s-2 K-1 en κ = 1.4.
Bereken
a: de doorsnede A* van de keel in cm2
b: de massastroom m uit het vat in kg s-1
Vraagstuk 15
In een raketmotor staat een
schok op de positie met een
doorsnede A = 0.25 m2. De
uitstroomopening Ae = 0.4 m2.
De doorsnede van de keel is Ak
= 0.2 m2. Bereken: de
stuwkracht F in kN tengevolge
van het uitstromende gas.
Ak
De gasconstante voor het gas is R = 355 m2 s-2 K-1 en κ = 1.4.
Ae
Vraagstuk 16
Een dunne staaf doorboort het oppervlak van de
stroming in een rechthoekig kanaal en creëert op
het oppervlak een wigvormige golf met een halve
tophoek α = 25 ° . De diepte van het kanaal is 35
cm.
De g = 9.81 m s-2 .
Bereken
a: de snelheid V in het kanaal in m s-1.
b: de kritieke diepte y c in m
V
α
Vraagstuk 17
Een verhoging h die 10 cm hoog
is veroorzaakt een hydraulische
sprong bovenstrooms van de
verhoging. De waterdiepte ter
plaatse van doorsnede 3 is
y3 = 35 cm
y3
V1
De stroming mag als wrijvingsloos beschouwd worden behalve in de hydraulische
sprong.
De g = 9.81 m s-2 .
Bereken de snelheid V1 voor de hydraulische sprong
Vraagstuk 18
Water wordt verpompt met een centrifugaal pomp waarvan het toerental
n = 1750 omw/min is. De impeller heeft achterwaarts gekromde vanen
met een uittree hoek van β2 = 60°. De breedte van de pomp is b2 = 12.5
mm. Het volume debiet is Q = 80 m2 hr-1 en de radiale uitstroomsnelheid
is vn2 = 3.6 m s-1.
Wat wordt de opvoerhoogte H in m als de pomp op een toerental
n2 = 1170 wordt afgesteld terwijl we stellen dat de pomp op zijn
werkpunt blijft
Tevens geldt dat g= 9.81 m s-2.