Vraag 1 - Medica

1ste Bachelor ARTS of TANDARTS
Academiejaar 2004-2005
BIOFYSICA: Toets II.2. Arbeid en energie : Oplossingen
Vraag 1
Een blok met massa m1 = 4 kg kan over een hellend vlak schuiven,
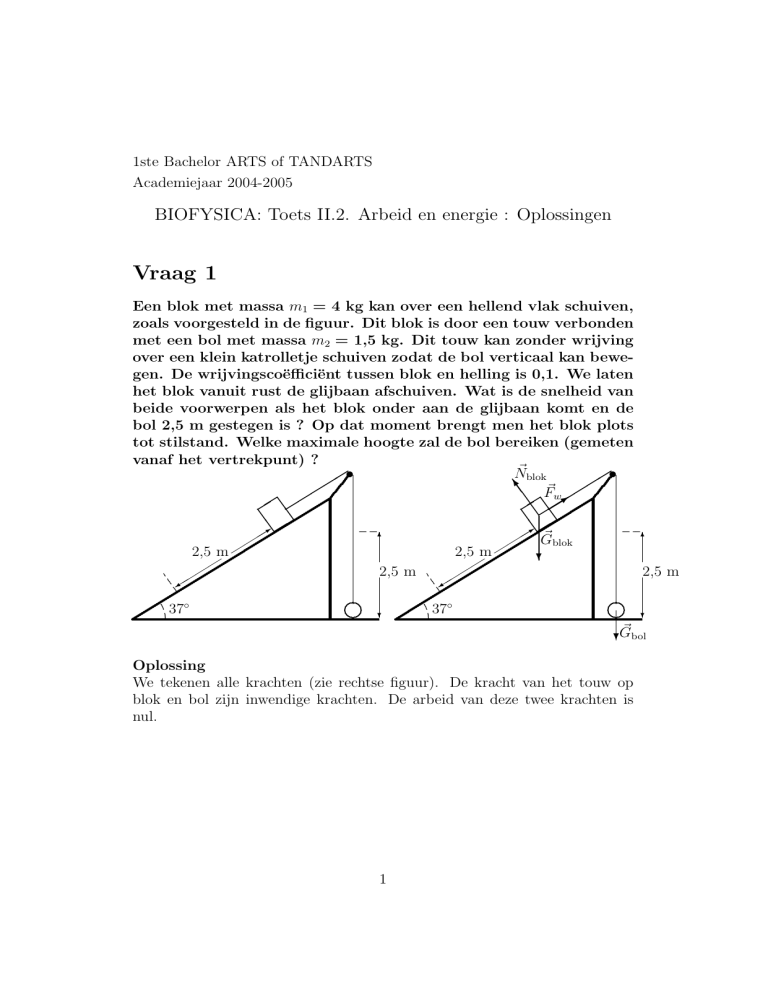
zoals voorgesteld in de figuur. Dit blok is door een touw verbonden
met een bol met massa m2 = 1,5 kg. Dit touw kan zonder wrijving
over een klein katrolletje schuiven zodat de bol verticaal kan bewegen. De wrijvingscoëfficiënt tussen blok en helling is 0,1. We laten
het blok vanuit rust de glijbaan afschuiven. Wat is de snelheid van
beide voorwerpen als het blok onder aan de glijbaan komt en de
bol 2,5 m gestegen is ? Op dat moment brengt men het blok plots
tot stilstand. Welke maximale hoogte zal de bol bereiken (gemeten
vanaf het vertrekpunt) ?
~ blok
N
qqqtq
qqqqqtq
q
qqqqqq
]
J
qqqqq
~w qqqqqqqqq
F
q
qqq
qqq
J
J qqqqqqqqq
J J
qqqqqq
qqqqqq
q
q
J
q
q
3
qqqqq
qqqqqq
q
q
q
q
q
2,5 mqqqq
qqqqq
qqq
q
q
q
q
..
qqqqqq
....
..
qqqqq
q
q
+
....
q
q
q
.q
qqqq.q
qq...q..qqq ◦
q
q
q
q
qqq 37
qqqqqq .....
3 qqqqqq
J
J
qqqqq
J J
qqqqqq
q
q
q
q
Jqqq
qqq
......... .........
3
~ blok
qqqqq G
q
6
q
q
q
q
qqq
2,5 mqqqq
qq qqqq
?
q
qqqqq
q
q
q
q
2,5 m ...... q
q
qqqq
..
+qqqqq
....
.q.qqqq
q
qqqqqq
..........
qqqqqq...... 37◦
q
..... ....
q
q
q
..
..........
? qqqqq
..
......... .........
6
2,5 m
..........
..... ....
..........
~
?
Gbol
?
Oplossing
We tekenen alle krachten (zie rechtse figuur). De kracht van het touw op
blok en bol zijn inwendige krachten. De arbeid van deze twee krachten is
nul.
1
Gegevens
• m1 = 4 kg
• m2 = 1.5 kg
• f = 0.1
• ∆ yblok = −2, 5 sin 37◦ m
• ∆ ybol = 2, 5 m
• v1,blok = v1,bol = 0 m/s
Er is maar één niet-conservatieve kracht die uigeoefend wordt op het systeem
en dat is de wrijvingkracht op het blok. We hebben dus:
W12 (F~w ) = E2 − E1
Nu is Nblok = m1 g cos 37◦ en dus Fw = f Nblok = f m1 g cos 37◦ . We kunnen hiermee de arbeid geleverd door de wrijvingskracht berekenen. Merk
op dat die negatief moet zijn aangezien deze kracht tegengesteld is aan de
bewegingsrichting.
W12 (F~w ) = −f m1 g (cos 37◦ ) 2, 5.
We moeten het verschil in energie nog berekenen. Dit is de som van het
verschil in potentiële energie en het verschil in kinetische energie.
E2 − E1 = ∆Ep + ∆Ek = ∆Ep,blok + ∆Ep,bol + ∆Ek .
Dit geeft
−f m1 g (cos 37◦ ) 2, 5 = m1 g ∆yblok + m2 g ∆ybol +
m1 + m2 2
(v2 − v12 )
2
of
v2 = [
1
2
(−f m1 g (cos 37◦ ) 2, 5−m1 g ∆yblok −m2 g ∆ybol )] 2 = 2, 29 m/s
m1 + m2
2
Als het blok dan tot stilstand word gebracht, heeft de bol een snelheid naar
omhoog gericht en zal dus in die richting voortbewegen. Er zijn geen nietconservatieve krachten meer. We kunnen dus de wet van behoud van energie
gebruiken. Noem 2 de situatie als het blok wordt gestopt en 3 de situatie als
de bol zijn maximale hoogte heeft bereikt. Dan hebben we
• v2 = 2, 2 m/s
• y2 = 2.5 m
• v3 = 0 m/s(de snelheid van de bol die omhoog gericht is zal afnemen omwille van de negatieve versnelling veroorzaakt door de zwaartekracht. Als de bol zijn maximale hoogte heeft bereikt zal zijn snelheid
0 worden en dan van teken omklappen, de bol valt terug naar beneden)
We hebben dus
m2 v22
+ m2 g y 2 = m2 g y 3
2
of
y3 = y2 +
v22
= 2, 77m
2g
3
Vraag 2
Een bolletje met massa 0,20 kg is vastgemaakt aan een touw en beschrijft een
cirkelbaan met middelpunt P in een verticaal vlak . De lengte van de touw
is 50 cm. In de laagste positie op de baan is de snelheid van het bolletje 6,72
m/s. Wat is de spankracht in het touw als het bolletje zich in de hoogste
stand (2) bevindt ?
x
2
......... ........... ......... ......
... ...
...
......
...
.......
....
..
...
....
.
....
.
.
.
....
.
..
..
.
..
.
...
..
...
...
...
..
...
.
...
...
...
..
..
.
.
...
...
...
...
..
...
..
..
..
.....
..
..
...
.
..
...
.
..
.
.
...
.
.
.
.
.
..
.
...
...
.
....
.
..
...
...
.
..
.
....
....
....
.
..
....
...
....
...
.
..
..
.
.
.
.
.
.
.
.
......
.
.. .
.. .
.
.......
........
...
........
......... .
........ .
........ .......... ......... ..
.........
.........
.......
. ..
......
sP
h
2
x
......... ......... ......... ......
... ...
..
......
.......
..
....
.
.
.
.
....
.
..
..
..
...
...
...
..
..
.
.
...
...
...
.
..
.
.
...
...
...
..
..
..
..
..
..
..
..
....
.
..
..
.
.
..
.
.
...
.
.
.
.
.
..
.
...
...
.
....
.
..
...
...
.
..
.
....
....
....
.
..
....
...
....
...
.
..
..
.
.
.
.
.
.
.
.
......
.
.. .
.. .
.
.......
........
...
........
......... .
........ .
........ .......... ......... ..
.........
.........
.......
. ..
......
...
.
...
T~ ?
... ~
... G
...
?
sP
T~ 0
6
1
h
~
G
?
Oplossing
We schrijven eerst de gegevens neer
• m = 0, 20 kg
• R = 0.50 m
• f = 0.1
• v1 = 6, 72 m/s
We moeten de spankracht berekenen in situatie 2. Hiervoor passen we de
tweede wet van Newton toe
~ + T~
m~a = G
Projectie op de normale as geeft ons m an = m g + T . We weten ook dat
v2
an = R2 zodat
v2
T = m 2 − mg
R
Om de spankracht te berekenen moeten we de snelheid kennen. Die kunnen
we vinden met de wet van behoud van energie. We hebben
E1 = E2
4
of
m v22
m v12
+ mg2R =
.
2
2
Waaruit we halen
m v22
R
=
m v12
R
− mg4 = 10, 21 N.
Als we dit invullen krijgen we de grootte van de spankracht
T = −m g +
m v2
= 8, 25N
R
Vraag 3
Teken het elektrisch veld in punt A. Verklaar je antwoord.
.
..........................................................................................
.................
............
...........
............
...........
..........
.
.
.
.
.
.
.
.
.
......
......
.......................................
........
..........
.
.
.
.
.
.
.......
....
.
.
.
.
.
.
......
....
.
.
.
.
.
.
.
.
.
....
........ ............
...
....
....
...
....
....
....
....
...
....
...
...
....
...
..
...
.
.
.
...
.
.
.
...
.
...
...
.
.
.
.
...
..
.
..
.
.
...
..
.
...
..
.
...
....
...
...
..
...
...
...
...
...
....
...
..
rA
−10 V
−5 V (maximale spanning)
−10 V
De elektrische potentiaal is maximaal in punt A. We hebben dus dat
∂V
∂V
∂V
=
=
=0
∂x
∂y
∂z
en dus
~ = −∇V
~ = (0, 0, 0).
E
Of Ex = − dV
en we kiezen een x-as door A loodrecht op het equipotentiaaldx
oppervlak. In een maximum is de afgeleide nul, dus ook het veld.
Het veld in A kan ook gezien worden als de som van twee elektrische veldvectoren, die tegengesteld gericht zijn en dezelfde grootte hebben.
5