Opgave 1 Elektrocardiogram H92-I-1

Natuurkunde Havo 1992-I
Opgave 1 Elektrocardiogram
De samentrekking van de hartspier wordt veroorzaakt door elektrische spanningen. Die spanningen
kunnen geregistreerd worden als functie van de tijd. Zo'n registratie wordt een elektrocardiogram
(ECG) genoemd. Een ECG verschaft inzicht in het functioneren van het hart.
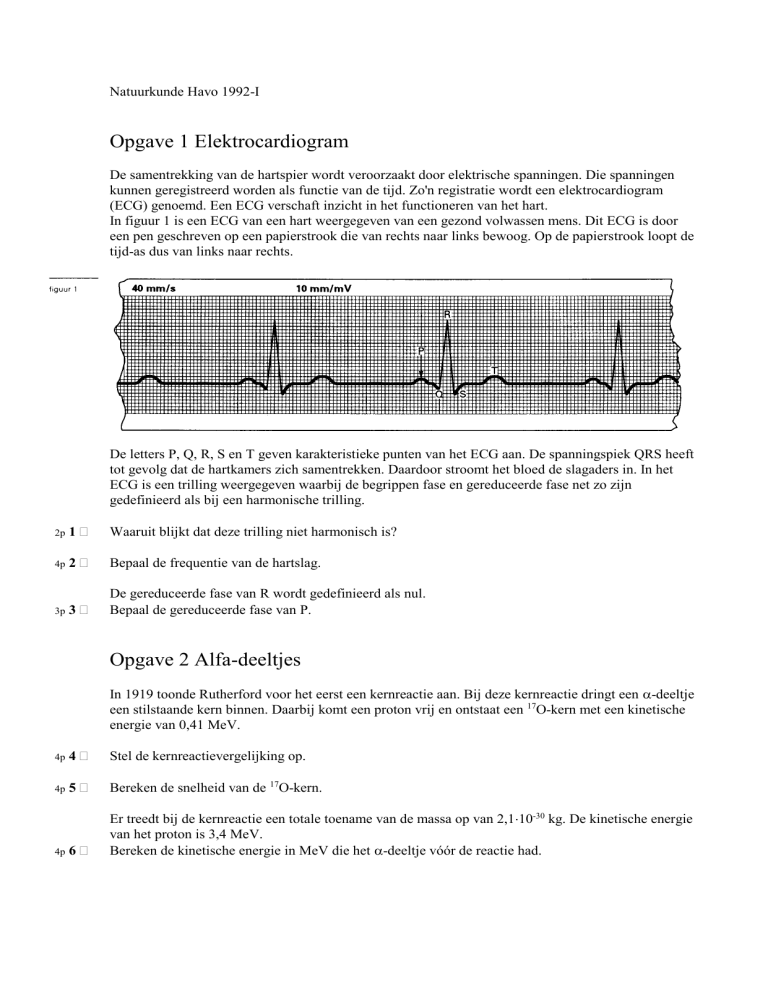
In figuur 1 is een ECG van een hart weergegeven van een gezond volwassen mens. Dit ECG is door
een pen geschreven op een papierstrook die van rechts naar links bewoog. Op de papierstrook loopt de
tijd-as dus van links naar rechts.
De letters P, Q, R, S en T geven karakteristieke punten van het ECG aan. De spanningspiek QRS heeft
tot gevolg dat de hartkamers zich samentrekken. Daardoor stroomt het bloed de slagaders in. In het
ECG is een trilling weergegeven waarbij de begrippen fase en gereduceerde fase net zo zijn
gedefinieerd als bij een harmonische trilling.
2p
1
Waaruit blijkt dat deze trilling niet harmonisch is?
4p
2
Bepaal de frequentie van de hartslag.
3
De gereduceerde fase van R wordt gedefinieerd als nul.
Bepaal de gereduceerde fase van P.
3p
Opgave 2 Alfa-deeltjes
In 1919 toonde Rutherford voor het eerst een kernreactie aan. Bij deze kernreactie dringt een -deeltje
een stilstaande kern binnen. Daarbij komt een proton vrij en ontstaat een 17O-kern met een kinetische
energie van 0,41 MeV.
4p
4
Stel de kernreactievergelijking op.
4p
5
Bereken de snelheid van de 17O-kern.
6
Er treedt bij de kernreactie een totale toename van de massa op van 2,110-30 kg. De kinetische energie
van het proton is 3,4 MeV.
Bereken de kinetische energie in MeV die het -deeltje vóór de reactie had.
4p
Opgave 3 Aluminium ring
In een spoel bevindt zich een weekijzeren kern.
Via een schakelaar S kan de spoel op een gelijkspanningsbron worden aangesloten. Als S gestoten
wordt, ontstaat in de weekijzeren kern een magnetisch veld. In figuur 2 zijn enkele veldlijnen
getekend.
3p
3p
7
8
Naast de spoel hangt een aluminium ring. Schakelaar S wordt geopend, en na enige tijd weer gesloten.
Direct na het sluiten van S ontstaat een inductiestroom in de ring.
Leg uit of de inductiestroom van F via G naar H loopt of van H via G naar F.
Zolang er een inductiestroom loopt, ondervindt de ring een lorentzkracht.
Figuur 2 staat ook op de bijlage. Punt H ligt op de onderkant van de ring.
Teken in de figuur op de bijlage de richting van de lorentzkracht in punt H op de ring.
Geef op de bijlage ook een toelichting.
Bijlage:
Opgave 4 Tralie
3p
4p
4p
9
Op een tralie valt een evenwijdige bundel
monochromatisch licht. Dit licht wordt door het
tralie in een aantal bundels gesplitst. Deze bundels
worden met behulp van een lens met een
brandpuntafstand van 75,0 cm scherp afgebeeld op
een scherm. In figuur 3 is een gedeelte van de
stralengang van een bundel van de eerste orde
getekend. Het optische midden van de lens is
aangegeven met de letter O. Figuur 3 staat vergroot
op de bijlage.
Construeer in de figuur op de bijlage het verloop
van de zeven lichtstralen tot aan het scherm.
10 
Punt M ligt op de hoofdas van de lens. Het eerste
orde maximum ontstaat in een punt scherm P op het
scherm. De afstand MP is 28,3 cm.
De tralieconstante d is 1,6710-6 m.
Bereken de golflengte van het gebruikte licht.
11 
Men wil de afstand tussen M en het eerste orde maximum bij dit licht en dit tralie vergroten.
Leg uit wat men achtereenvolgens moet doen om dit te bereiken.
Bijlage:
Opgave 5 Woonhuisverwarming
4p
12 
Een vrijstaand huis is opgetrokken uit muren en vloeren van beton. In het huis is 1,2105 kg beton
verwerkt.
Om de betonnen muren is een 'isolatiedeken' aangebracht, waarna de buitenmuren van baksteen zijn
gemetseld. In het huis bevindt zich 400 m3 lucht.
Op een zeker moment is de temperatuur van die lucht èn van het beton 8,0 °C. Dan wordt de
verwarming ingeschakeld. Men wil de temperatuur van de lucht in het huis laten stijgen tot 20,0 °C.
De gemiddelde temperatuur van het beton is dan 15,0 °C. De soortelijke warmte van het beton is
0,90103 J/(kgC), die van de lucht is 1,0103 J/(kgC).
Toon door berekening aan dat het veel meer warmte kost om het beton te verwarmen dan om de lucht
te verwarmen.
Een woning die op de gewenste temperatuur is, kan men op temperatuur houden door de
warmteverliezen via de ramen, de muren en het dak te compenseren door het huis te verwarmen.
Om met deze warmteverliezen te kunnen rekenen, heeft men de warmtedoorgangscoëfficiënt K
ingevoerd. Deze K geeft aan hoeveel warmte er per seconde door een oppervlakte van 1 m2 verdwijnt
bij een temperatuurverschil van 1 °C. De eenheid van K is W/(m2°C). Deze warmteverliezen kunnen
met onderstaande formule worden berekend:
P = K A T
Hierin is:
 P de energie (warmte) die per s verdwijnt (in watt)
 A de oppervlakte (in m2) waar de warmte doorheen stroomt
 T het temperatuurverschil (in °C) tussen binnen en buiten.
4p
13 
De oppervlakte van de muren is 114 m2.
De K-waarde voor deze muren is 0,80 W/(m2°C).
Een stookseizoen duurt in Nederland 250 dagen. Gedurende het stookseizoen is het
temperatuurverschil tussen binnen en buiten gemiddeld 13,0 °C.
Bereken de warmte die in een stookseizoen door de muren naar buiten gaat.
De totale warmteverliezen zijn in een stookseizoen 5,61010 J.
De ketel van de c.v. wordt gestookt met aardgas. Bij de verbranding van l,0 m3 aardgas komt een
warmte vrij van 35 MJ.
Het nuttig effect (rendement) van de ketel is 90%.
3p
14 
Bereken hoeveel m3 aardgas er per stookseizoen nodig is voor verwarming.
3p
15 
Bereken hoeveel procent aardgas er bespaard had kunnen worden als de thermostaat tijdens het hele
stookseizoen 1,0 °C lager was gezet.
Opgave 6 Halogeenlampen
3p
16 
Voor verlichting worden steeds vaker halogeenlampen gebruikt. De temperatuur van de gloeidraad is
hoger dan bij een gewone gloeilamp. Daardoor geven ze meer licht. De lampen zijn gevuld met een
gas dat er voor zorgt dat de gloeidraad bij deze hogere temperatuur nauwelijks verdampt.
Een halogeenlamp wordt aangesloten op een spanning van 12,0 V, waarbij zijn vermogen 40 W
bedraagt.
Bereken de weerstand van de gloeidraad van deze halogeenlamp tijdens het branden.
Om een dergelijke lamp op het lichtnet van 220 V wisselspanning aan te kunnen sluiten, is een
transformator nodig. Er wordt hiervoor een transformator gebruikt, die we als ideaal beschouwen. De
primaire spoel heeft 3000 windingen.
3p
17 
Bereken het aantal windingen van de secundaire spoel.
3p
18 
Bereken de stroomsterkte in de primaire spoel.
In figuur 4 is te zien hoe een halogeenlamp is opgehangen.
Twee metalen kabels zijn evenwijdig aan elkaar van muur tot muur gespannen. De kabels hebben een
doorsnede met een oppervlakte van 2,0 mm2. Via een transformator wordt tussen de kabels bij A en B
een wisselspanning van 12,0 V aangelegd.
Over iedere kabel wordt een soepele koperdraad gelegd. De koperdraden maken goed elektrisch
contact met de kabels en dienen voor de stroomvoorziening van de lamp. De koperdraden zorgen
eveneens voor de ophanging van de lamp. Om de lamp in evenwicht te houden zijn twee kogels
bevestigd aan de vrije uiteinden van de koperdraden. Op deze manier zijn twee verschillende lampen
L1, en L2 opgehangen. L1 hangt op 3,00 m van de muur, L2 hangt wat verder weg.
In figuur 5 is de elektrische schakeling schematisch weergegeven.
3p
4p
19 
De weerstand van 1,00 m metalen kabel is 1,410-2 .
Bereken de soortelijke weerstand van het metaal van de kabel.
20 
Door L1 gaat een stroom van 3,1 A en door L2 een stroom van 3,9 A. Verwaarloos de weerstand van
de koperdraden.
Bereken de spanning die in deze situatie over L1 staat.
In figuur 6 is de ophanging van lamp L1 nogmaals getekend.
4p
3p
21 
De massa van lamp L1 is 140 g. Elk van beide koperdraden maakt een hoek  met de verticale lijn
door de lamp. De massa van de koperdraden wordt verwaarloosd.
Bereken de spankracht in een stuk koperdraad tussen L1 en een kabel als hoek  gelijk is aan 35°.
22 
Door de kogels naar beneden te trekken is de lamp omhoog te brengen naar een nieuwe
evenwichtsstand. De spankracht in het verticale deel van de koperdraad tussen een kogel en de kabel
is dan weer even groot als voorheen.
Bij het omhoogbrengen van de lamp wordt hoek  groter. Daardoor wordt de spankracht in een
koperdraad tussen lamp L1 en een kabel groter. Deze spankracht is dus wel veranderd.
Leg uit hoe het mogelijk is dat, ook bij de hogere stand van de lamp, het geheel in rust blijft.
Let op: de laatste opgave van dit examen staat op de volgende pagina.
Opgave 7 Zonsverduistering
De maan draait in een baan rond de aarde. We nemen aan dat deze baan cirkelvormig is, met de aarde
als middelpunt.
De snelheid van de maan in haar baan rond de aarde is 1,02 km/s. Gegevens over de straal van de
maanbaan en over de massa van de maan zijn te vinden in tabel 31 van het informatieboek Binas.
3p
23 
Bereken de omlooptijd van de maan in haar baan rond de aarde.
3p
24 
Bereken de kracht waarmee de aarde de maan aantrekt.
De afstand van de aarde tot de zon is 1,501011 m. Met behulp van een positieve lens met een
brandpuntsafstand van 200 cm wordt een scherp beeld van de zon geprojecteerd op een scherm. De
diameter van dit beeld van de zon blijkt 1,8 cm te zijn.
3p
25 
Bereken hieruit de diameter van de zon.
Soms staat de maan tussen de aarde en de zon, en dan treedt een zonsverduistering op. In het geval dat
de schijf van de maan de hele schijf van de zon bedekt, spreekt men van een totale zonsverduistering.
In figuur 7 is de situatie waarbij een zonsverduistering plaatsvindt, schematisch voorgesteld. De
verhoudingen van de onderlinge afstanden en diameters zijn in de figuur niet in overeenstemming met
de werkelijkheid.
3p
3p
26 
27 
Figuur 7 staat ook op de bijlage.
Teken op de bijlage de stralen die het gebied op aarde bepalen waar een totale zonsverduistering te
zien is. Geef dat gebied met een pijltje aan.
Op plaatsen waar men een totale zonsverduistering waarneemt, is het niet helemaal donker. Er komt
daar dan nog licht dat afkomstig is van de gasvormige atmosfeer rondom de zon. Het spectrum van dit
licht bestaat uit een aantal lijnen. Eén van deze lijnen hoort bij een golflengte van 486 nm.
Bereken de energie van fotonen van dit licht.
Bijlage:
Einde.