09-05-18-Voorbeeldvragen voor proefwerk

Voorbeeldvragen voor proefwerk VWO-E2: Straling en Materie
1. Dubbelster.
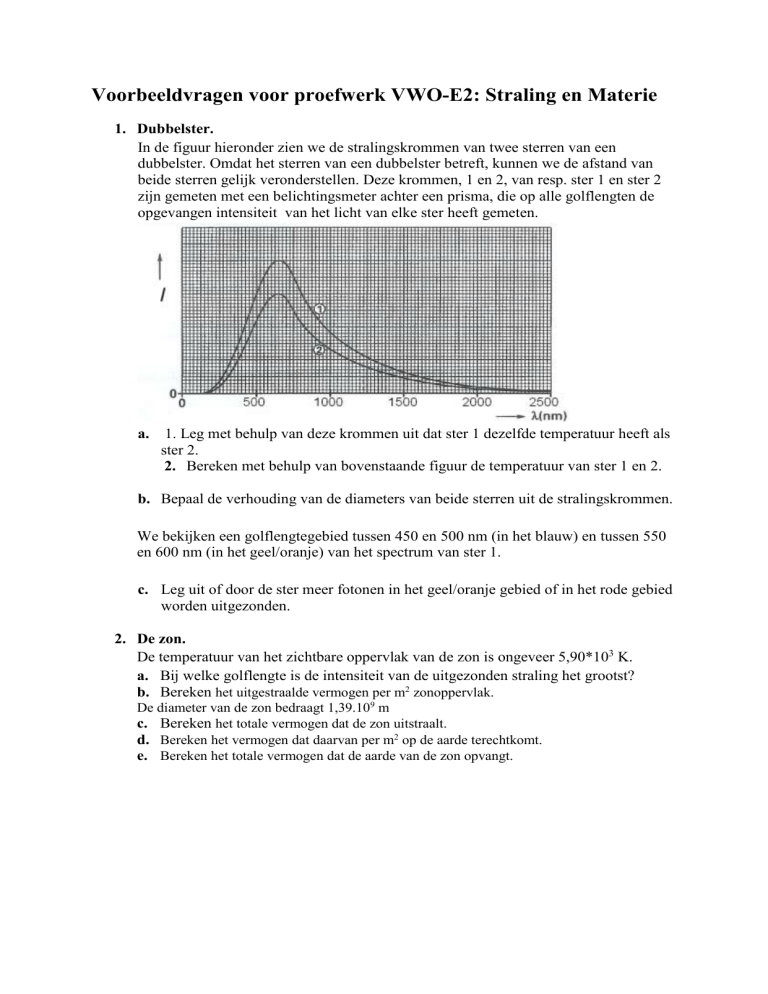
In de figuur hieronder zien we de stralingskrommen van twee sterren van een
dubbelster. Omdat het sterren van een dubbelster betreft, kunnen we de afstand van
beide sterren gelijk veronderstellen. Deze krommen, 1 en 2, van resp. ster 1 en ster 2
zijn gemeten met een belichtingsmeter achter een prisma, die op alle golflengten de
opgevangen intensiteit van het licht van elke ster heeft gemeten.
a.
1. Leg met behulp van deze krommen uit dat ster 1 dezelfde temperatuur heeft als
ster 2.
2. Bereken met behulp van bovenstaande figuur de temperatuur van ster 1 en 2.
b. Bepaal de verhouding van de diameters van beide sterren uit de stralingskrommen.
We bekijken een golflengtegebied tussen 450 en 500 nm (in het blauw) en tussen 550
en 600 nm (in het geel/oranje) van het spectrum van ster 1.
c. Leg uit of door de ster meer fotonen in het geel/oranje gebied of in het rode gebied
worden uitgezonden.
2. De zon.
De temperatuur van het zichtbare oppervlak van de zon is ongeveer 5,90*103 K.
a. Bij welke golflengte is de intensiteit van de uitgezonden straling het grootst?
b. Bereken het uitgestraalde vermogen per m2 zonoppervlak.
De diameter van de zon bedraagt 1,39.109 m
c. Bereken het totale vermogen dat de zon uitstraalt.
d. Bereken het vermogen dat daarvan per m2 op de aarde terechtkomt.
e. Bereken het totale vermogen dat de aarde van de zon opvangt.
3. Energieniveaus van een atoom.
Hiernaast zien we vier verschillende energieniveaus van
een denkbeeldig atoom.
a. Leg uit hoeveel verschillende spectraallijnen we
van het atoom kunnen identificeren, wanneer we
aannemen dat elektronen tussen alle niveaus
kunnen springen.
b. Een elektron springt van niveau n=4 naar n=3 en vervolgens direct naar de
grondtoestand n=1. Hierbij komen twee fotonen vrij. Het eerste foton heeft
frequentie f1, het tweede foton frequentie f2. Een ander elektron springt direct
van niveau n=4 naar n=1. Hierbij komt een foton vrij met frequentie f3. Toon
aan dat f1+f2=f3.
c. Bij elk van bovengenoemde frequenties hoort een golflengte, resp. λ1, λ2 en λ3. Toon
aan dat
d. Hoeveel spectraallijnen zou je waarnemen als de vier energieniveaus met n=1 t/m n=4
op gelijke afstanden van elkaar zouden liggen? Motiveer je antwoord.
4. Voorspelbare golflengte in het spectrum van waterstof?
In het spectrum van waterstof zijn van twee lijnen de frequenties bekend: 2,7.1014 Hz en
4,6.1014 Hz. Bij deze frequenties horen twee golflengtes. Bahez beweert dat op grond van
deze gegevens is te voorspellen dat er in ieder geval nog een golflengte in het spectrum van
waterstof moet voorkomen.
a. Bereken deze golflengte.
b. In welk gebied van het spectrum ligt deze golflengte?
5. Golflengten van fotonen uit een stralend atoom.
In het diagram hiernaast is het energieverschil tussen
niveau A en B tweemaal zo groot als die tussen niveau B
en C. Tijdens de sprong van niveau C naar B zendt het
elektron een foton uit met een golflengte van 600 nm.
a. Hoeveel bedraagt de golflengte van een foton bij een
energiesprong van niveau B naar niveau A?
b. En bij een energiesprong van niveau C naar niveau A?
6. Zonnezeil.
Met de kracht van fotonen afkomstig van de zon,
kunnen we in de ruimte een z.g. ‘zonnezeil’
aandrijven. Dat is cirkelvormig groot zeil van dun
reflecterend materiaal, die wordt aangedreven door
fotonen van de zon. De kracht die deze fotonen
uitoefenen is uitermate gering, maar voldoende om
dit zeil uiteindelijk een redelijke snelheid te geven.
Hierdoor zijn mogelijk in de toekomst lange reizen
langs diverse planeten te maken, zonder dat veel
brandstof nodig is.
Wanneer een foton van de zon loodrecht tegen het zonnezeil kaatst, wordt deze door
het zeil gereflecteerd, waardoor het zeil een (weliswaar zéér kleine) snelheidstoename
ondervindt.
a. Leg uit of de golflengte van het foton na de botsing iets groter of iets kleiner is
geworden.
We nemen aan dat voor het vervolg van de opgave de golflengteverandering van het
foton verwaarloosbaar is.
b. Bereken met de relatie van de Broglie dat een foton met een golflengte van 550
nm, dat door het zeil wordt teruggekaatst, een impulsverandering aan het zeil geeft
van 2,42*10-27 Ns.
De intensiteit van de zonnestraling vlakbij de aarde is
1,4*103 Wm-2. We nemen aan dat alle fotonen
loodrecht het zeil treffen. De vorm en maten van het
zeil staan in de figuur hiernaast (de oppervlakte van de
spleten is te verwaarlozen). Bovendien nemen we aan
dat de energie en de impuls van alle fotonen die het zeil
treffen, gelijk zijn aan die van een foton met een
golflengte van 550 nm.
c.
Bereken het aantal fotonen dat per seconde op het
zonnezeil terecht komt.
d. Bereken de totale kracht van de fotonen gedurende
één seconde op het zonnezeil.
7. Afstandsbepaling van een sterrenhoop.
Van twee open sterhopen,
Perseï en Praesepe zijn van
een aantal sterren het
opgevangen vermogen en de
oppervlaktetemperatuur
bepaald welke in het diagram
hiernaast zijn weergegeven.
De sterren van Perseï zijn
met kruisjes en de sterren
van Praesepe met cirkeltjes
aangegeven. De sterhoop
Perseï staat op een afstand
van 6,8*1019 m.
Bepaal op welke afstand de
sterhoop Praesepe zich
bevindt.
8. Pulserende ster.
Niet alle sterren hebben een
constante lichtkracht. Van een
bepaald type veranderlijke ster,
een Cepheïde (genoemd naar de
ster δ-Cepheï) variëren de straal
en de temperatuur periodiek,
waardoor ook de lichtkracht
periodiek verandert. Van een ster
is in de figuur de verhouding
tussen L(t) en Lminimum , de
kleinste waarde van L als functie
van de tijd weergegeven.
a. Leg uit dat de lichtkracht van de ster zowel afhankelijk is van de temperatuur als
van de straal van de ster.
Voor Cepheïden blijkt de gemiddelde lichtkracht, Lgem, evenredig te zijn met de
periode P van de variaties in de lichtkracht: Lgem = C*P, waarin C=1,8*1024 Ws-1 en
P de periode (in s).
b. Bepaal de gemiddelde lichtkracht, Lgem, van deze ster.
De intensiteit van de straling van deze ster is voor een waarnemer op de aarde
gemiddeld 1,1*10-9 W.
c. Bereken de afstand van deze ster tot de aarde.
Walter Baade, een Duits astronoom (1893-1960) onderscheidde in 1952 na uitgebreide
waarnemingen twee typen Cepheïden: Type I, waarvoor bovengenoemde relatie tussen
Lgem en P bestaat, en type II, waarvoor de constante C de waarde C=0,45*1024 Ws-1
heeft. Veronderstel dat de ster, zoals hierboven beschreven, niet van type I maar van
type II blijkt te zijn.
d. Beredeneer of de ster dan dichterbij of verder weg staat dan in c is berekend.
9. Snelheid van de ster Alpha Centauri.
Van de ster welke het dichtst bij de zon staat, Alpha Centauri, blijkt in het spectrum de
waterstoflijn een golflengte te hebben van 656,237 nm. Als de aarde en de ster ten
opzichte van elkaar stil zouden staan, dan is de golflengte gelijk aan 656,285 nm.
a. Beweegt de ster van ons af of naar ons toe?
b. Bereken de radiële snelheid van de ster ten opzichte van ons.
10. Gasontladingslampje
Een gasontladingslampje, dat wit licht uitstraalt, bevat ondermeer xenon. Dit lampje
wordt gestart door de xenonatomen erin te ioniseren. Dat kan door elektronen tegen
deze xenonatomen te laten botsen. Een elektron dat een potentiaalverschil doorloopt
van 1 volt, krijgt daardoor een kinetische energie van 1eV.
a. Leg uit, waarom over een dergelijk lampje daartoe een spanning moet worden
aangelegd van meer dan 12 volt.
Behalve xenon bevat dit lampje ook metaalzouten. Spoedig na het inschakelen
verdampen en ontleden deze metaalzouten door de warmteontwikkeling. De atomen in
deze damp stralen ook licht uit, waardoor wit licht uitgestraald wordt. In het diagram
hieronder is het uitgestraalde vermogen per nanometer uitgezet tegen de golflengte.
b. Beschrijf hoe met behulp van dit diagram het uitgestraalde vermogen van het
lampje kan worden bepaald. Je hoeft deze bepaling niet uit te voeren.
In het diagram zijn bij 312 nm en 405 nm pieken te zien die even hoog zijn. Het aantal
fotonen dat door een fotometer binnen een gebied van 1 nm rond 312 nm wordt
opgevangen, bedraagt 8,25.1016 per seconde.
c. Bereken het aantal fotonen, dat per seconde binnen een gebied van 1 nm rond 405
nm door de fotometer wordt opgevangen.
Juliette merkt op dat er volgens haar in het ontladingslampje ook kwik (Hg) bevindt.
d. Beredeneer met gebruikmaking van bovenstaand diagram of zij gelijk heeft. Geef
uitleg!
11. P.m.
Antwoord vraag 1 - Dubbelster:
a. 1. De temperatuur van elk van beide sterren is te herleiden uit λmax, de golflengte,
waarop de stralingsintensiteit maximaal is. Deze is voor beide sterren hetzelfde. Dat
betekent dat de temperatuur van beide sterren hetzelfde is.
2. Lees af bij curve 1 of 2: λmax = 650 nm. Met de verschuivingswet van Wien
volgt dan voor de temperatuur van elk van beide sterren: 4,5.103 K.
b. Voor de intensiteit van beide sterren geldt:
met:
I1,I2
de ontvangen stralingsintensiteiten van ster 1 resp. ster 2
P1,P2 het uitgestraalde vermogen van ster 1 resp. ster 2
d1,d2
de afstanden van beide sterren, die zijn gelijk
Het totaal uitgestraalde vermogen van elke ster is evenredig met de oppervlakte en
met T4. Omdat de temperaturen van beide sterren gelijk zijn, is dat vermogen in dit
geval alleen evenredig met de oppervlakte.
Dus ook het uitgestraalde vermogen op iedere golflengte is evenredig met de
oppervlakte.
Uit de figuur volgt:
Dus de diameter van ster 1 is
.
1,12 maal die van ster 2.
c. Het oppervlak onder de curve is voor het golflengtegebied van 450 -500 nm kleiner
dan voor het golflengtegebied van 550-600 nm. Dit is in de figuur te zien.
Bovendien is het zo dat de energie van een foton groter is naarmate de golflengte
afneemt. Beide argumenten samen leiden ertoe dat het aantal fotonen uit het 450500 nm gebied kleiner is dan het aantal fotonen uit het 550-600 nm gebied.
Antwoord vraag 2 - De zon:
a. Volgens de verschuivingswet van Wien geldt:
Dus voor de
golflengte waarop de intensiteit van de uitgezonden straling het grootste is, geldt:
b. De Volgens de wet van Stefan-Boltzman geldt:
c. Het totale vermogen van de zon is het uitgestraalde vermogen per m2 maal het
oppervlak van de zon. Deze bedraagt:
. Het totale vermogen dat de zon
uitstraalt is dan:
d. De afstand van de aarde tot de zon bedraagt: 1,5.1011 m. Het totaal uitgestraalde
vermogen van de zon wordt dus verdeeld over een denkbeeldig boloppervlak van
. Per vierkante meter is dat:
e. De (geprojecteerde) oppervlakte van de aarde bedraagt:
Dit betekent, dat de aarde een vermogen
opvangt van
Antwoord vraag 3 - Energieniveaus van een atoom.
a. In totaal 6, nl. 1↔2, 1↔3, 1↔4, 2↔3, 2↔4, 3↔4,
b. Er geldt, dat E4↔3+E3↔1=E4↔1 en omdat geldt, dat E=h.f, volgt:
h.f1+h.f2=h.f3, dus f1+f2=f3.
c. Er geldt, dat E4↔3+E3↔1=E4↔1 en omdat geldt, dat
, volgt:
Dus
d. Er zal slechts één spectraallijn zichtbaar zijn, omdat alle fotonen bij gelijke
energiesprong dezelfde energie hebben, dus dezelfde frequentie en dezelfde
golflengte.
Antwoord vraag 4 - Voorspelbare golflengte in het spectrum van waterstof?
a. Bij de frequenties van de fotonen behoren de volgende energieën:
en
Totaal is dat een hoeveelheid energie van 4,84.10-19 J.
Een elektron kan ook rechtstreeks een sprong maken met een energieverschil van
4,84.10-19 J. De golflengte van het bijbehorende foton bedraagt dan:
dus
b. In het blauw-violette gebied.
Antwoord vraag 5 - Golflengten van fotonen uit een stralend atoom.
a.
Van B naar A is de energie van het foton tweemaal zo groot. De golflengte is dus
twee maal zo klein, dus 300 nm.
b. Van C naar A is de energie van het foton driemaal zo groot. De golflengte is dus
driemaal zo klein, dus 200 nm.
Antwoord vraag 6 - Zonnezeil.
a.
Voor de golflengte λ van een foton geldt:
. Omdat het foton kennelijk
wat energie afstaat aan het zeil, wordt Ef kleiner. Dat betekent dat λ iets toeneemt.
b.
Voor de impulsverandering van het foton geldt:
, waarbij pf de
impuls van het foton is (de factor 2 komt vanwege het feit dat de richting van het foton
omkeert).
Er geldt:
dus
, zodat
Invullen
geeft:
Volgens de wet van behoud van impuls is dat gelijk aan de impulsverandering van het
zonnezeil.
c.
De energie per foton bedraagt voor een golflengte van 550 nm:
3,61*
e totale energie, die op per seconde
op het zeil valt bedraagt
Met:
En:
De opgevangen energie per sec bedraagt dus
Het aantal fotonen, dat per seconde het zeil treft, bedraagt dan:
d.
Het aantal fotonen, dat per seconde het zeil treft, is 2,74*1024 (zie vraag c). Er
geldt:
. In vraag b is berekend, dat ieder foton het zeil een
impulsverandering geeft van
. Iedere seconde ondervindt het
zeil dus een kracht van
Antwoord vraag 7 – Afstandsbepaling van een sterrenhoop.
We trekken twee rechte lijnen, zo goed mogelijk door beide groepen sterren en
bepalen dan voor een en dezelfde temperatuur de verhouding tussen het ontvangen
vermogen: deze bedraagt 170. Omdat de helderheden zich verhouden als het kwadraat
van de afstand, moet de sterrenhoop Praesepe zich op een afstand bevinden van
.
Antwoord vraag 8 – Pulserende ster.
a. Zoals in hoofdstuk 1 duidelijk is geworden, geldt voor de totale lichtkracht van een
ster:
. Hieruit kunnen we afleiden, dat zowel het oppervlak: (
)
als de temperatuur T bepalend is voor de lichtkracht van een ster.
b. Lgem =C*P
met: C=1,8*1024 Ws-1
P=6,0 dagen=6,0*24*60*60=5,18*105 s
Zodat Lgem=9,3*1029 W.
c. De afstand van de ster tot de aarde berekenen we met de kwadratenwet:
dus
of
d. De constante C is voor type II Cepheïden kleiner dan voor type I. Daar Lgem=C*P,
geldt dat Lgem kleiner is dan werd aangenomen. Dan is volgens
de afstand r kleiner. Dus staat de ster dichterbij dan aanvankelijk werd gedacht.
Antwoord vraag 9 – Snelheid van de ster Alpha Centauri.
a. Omdat de gemeten golflengte korter is dan de werkelijke golflengte, is er sprake
van een ‘blauwverschuiving’, d.w.z. de ster beweegt naar ons toe.
b.
Antwoord vraag 10 – Gasontladingslampje.
a. Volgens Binas – tabel 22 is de ionisatie-energie van xenon (Xe) 12,13 eV. Om
xenonatomen te ioniseren zal een ioniserend elektron dus minstens een energie van
12,13 eV moeten hebben. De spanning moet dus groter zijn dan 12,13 V.
b. Het door het lampje uitgezonden vermogen komt overeen met de oppervlakte
onder het diagram in het golflengtegebied van het zichtbare licht.
c. Het door de fotometer opgevangen vermogen is voor 312 nm even groot als voor
405 nm: immers de pieken zijn even hoog.
Dus voor het aantal fotonen, n, geldt:
n312U312=n405U405
of:
d. In Binas – tabel 20, de spectraalplaten, zijn de golflengten van de Hg-lijnen te
herkennen. Alle lijnen, die in het emissiespectrum van plaatje 10 zijn te zien,
komen ook in het diagram voor. Dus het is aannemelijk dat zich in het
gasontladingslampje kwik bevindt.