Vraagstuk 2 Een kanonkogel wordt afgevuurd en
advertisement
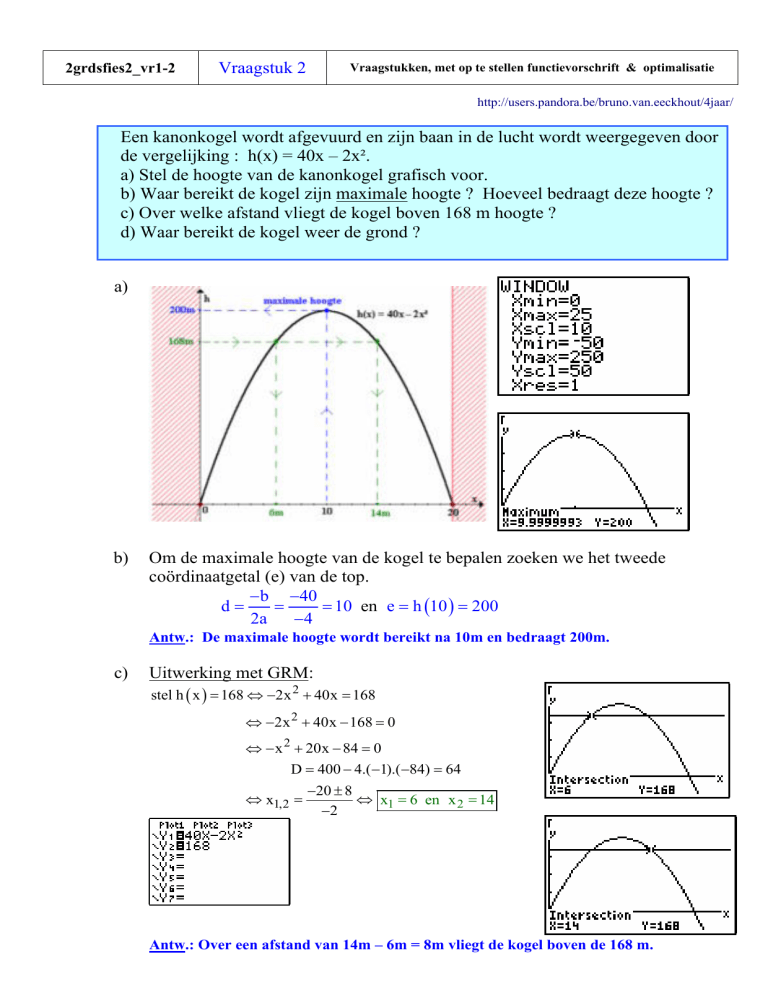
2grdsfies2_vr1-2 Vraagstuk 2 Vraagstukken, met op te stellen functievorschrift & optimalisatie http://users.pandora.be/bruno.van.eeckhout/4jaar/ Een kanonkogel wordt afgevuurd en zijn baan in de lucht wordt weergegeven door de vergelijking : h(x) = 40x – 2x². a) Stel de hoogte van de kanonkogel grafisch voor. b) Waar bereikt de kogel zijn maximale hoogte ? Hoeveel bedraagt deze hoogte ? c) Over welke afstand vliegt de kogel boven 168 m hoogte ? d) Waar bereikt de kogel weer de grond ? a) b) Om de maximale hoogte van de kogel te bepalen zoeken we het tweede coördinaatgetal (e) van de top. − b −40 d= = = 10 en e = h (10 ) = 200 2a −4 Antw.: De maximale hoogte wordt bereikt na 10m en bedraagt 200m. c) Uitwerking met GRM: stel h ( x ) = 168 ⇔ −2x 2 + 40x = 168 ⇔ −2x 2 + 40x − 168 = 0 ⇔ − x 2 + 20x − 84 = 0 D = 400 − 4.(−1).(−84) = 64 −20 ± 8 ⇔ x1,2 = ⇔ x1 = 6 en x 2 = 14 −2 Antw.: Over een afstand van 14m – 6m = 8m vliegt de kogel boven de 168 m. d) stel h ( x ) = 0 ⇔ −2x 2 + 40x = 0 ⇔ − x 2 + 20x = 0 ⇔ x ( − x + 20 ) = 0 ⇔ x1 = 0 en x 2 = 20 Antw.: De kogel bereikt de grond op een afstand van 20 m.
