Het dynamische gedrag van onregelmatige bandslijtage

Het dynamische gedrag van
onregelmatige bandslijtage
R.G.J. Rijkers
DCT 2008.079
Bachelor eindproject
Coaches:
Dr. Ir. I.J.M. Besselink
Ir. H. E. van Benthem (Vredestein)
Supervisor:
Prof. Dr. H. Nijmeijer
Technische Universiteit Eindhoven
Department Mechanical Engineering
Dynamics and Control Group
Eindhoven, April, 2008
Samenvatting
Onregelmatige bandslijtage is een complex fenomeen, omdat er erg veel factoren een
rol spelen. In samenwerking met bandenfabrikant Vredestein wordt in dit rapport
voortgeborduurd op eerder onderzoek van masterstudent Janno Veen. De centrale
vraag in dit onderzoek luidt: Wat is de oorzaak van onregelmatige bandslijtage en wat
kan er aan gedaan worden om het te voorkomen?
De door Janno Veen gebruikte laterale Magic Formula is vervangen door een
rigid ring model dat de verschillende relatieve translaties en kantelbewegingen tussen
band en velg modelleert. Met behulp van het bestaande bandmodel van J. Veen kan
slijtage worden gesimuleerd met het nieuw dynamisch lateraal bandmodel. De
verschillen tussen het gebruikte laterale bandmodel en de Magic Formula zijn echter
niet overtuigend. Met het nieuwe model is er nog steeds sprake van een statische
versterking met bijna verwaarloosbare fasedraaiing. De dwarskracht is met dit model
wel een factor twee hoger dan met de Magic formula wat ook twee keer meer slijtage
tot gevolg heeft.
Vervolgens is voor beter begrip van het lokale slijtmechanisme een
borstelmodel ontwikkeld. Dit model werkt met lange en korte rubberen blokjes die
het loopvlak van de band simuleren. Met een oneindig stijve bandgordel kunnen
eenvoudig krachten en verplaatsingen worden berekend per discrete tijdsstap. Deze
informatie wordt dan gebruikt voor de bepaling van slip en slijtage per blokje. Vooral
voor kleine sliphoeken bij bepaalde verticale krachten en blokdimensies is duidelijk
te zien dat een korter blokje meer slijt dan een lang blokje. Dit leidt uiteindelijk tot
onregelmatige slijtage, doordat een afgesleten stuk band relatief meer slijt dan de rest
van de band.
Een suggestie voor verder onderzoek naar onregelmatige slijtage is het
toepassen van een slijtagemodel met meerdere contactpunten zoals het gebruikte
borstelmodel terwijl krachtvariaties ook in acht worden genomen zoals bij het rigid
ring bandmodel. De parameters van het borstelmodel zouden gevalideerd moeten
worden zodat er meer inzicht wordt verkregen over de precieze werking van het
slijtagemechanisme en zodat men ook meer kan zeggen over de betrouwbaarheid van
de absolute resultaten. Voor beter begrip zou ook meetdata van translaties en
hoekkantelingen bij een onregelmatig slijtende autoband van pas komen.
2
Inhoudsopgave
1
Inleiding
1.1
Motivatie
1.2
Aanpak van dit onderzoek
4
4
5
2
Dynamisch lateraal bandmodel
2.1
Aanpak en beperkingen van het model van J. Veen
2.2
Ontwikkeling van het dynamisch lateraal bandmodel
2.3
Resultaten van het dynamisch lateraal bandmodel
6
6
9
12
3
Alternatief slijtagemodel
3.1
Probleem en globale aanpak
3.2
Modelvorming
3.3
Resultaten van het borstelmodel
15
15
15
16
4
Conclusies en aanbevelingen
4.1
Conclusies
4.2
Aanbevelingen
20
20
21
Referenties
22
Symbolenlijst
23
A
25
Bewegingsvergelijkingen van het verticale bandmodel
B.1 Parameterlijst van het model van J. Veen
26
B.2 Parameterlijst van het dynamisch lateraal bandmodel
27
C
Implementatie van het borstelmodel
28
D
Parameterlijst van het borstelmodel
31
E
State-space vorm van het dynamisch lateraal bandmodel
32
3
1
Inleiding
1.1
Motivatie
Behalve aërodynamische krachten en zwaartekracht worden alle grote krachten op
een auto via het contactoppervlak tussen band en weg uitgeoefend. Daarom is het
belangrijk dat het gedrag van de banden en het contact goed begrepen worden. Een
complex fenomeen in de bandenwereld is cupping. Dit is een vorm van
onregelmatige bandslijtage, die vooral optreedt op de achteras van
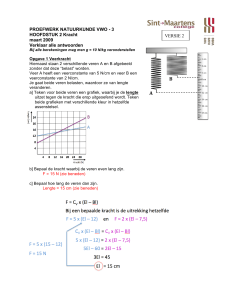
voorwielaangedreven auto’s. Van een gecupte band is sprake als er een hoogteverschil
ontstaat in de profielblokken op de schouder van de band. Zie figuur 1.1.
Figuur 1.1: Cupping [1]
De precieze oorzaak en maatregelen die moeten worden genomen zijn niet bekend.
Bandslijtage is al lastig te voorspellen, laat staan onregelmatige bandslijtage. Er
spelen zo veel factoren mee dat het probleem erg complex is. Afstudeerder Janno
Veen heeft een dynamisch model gemaakt, waarmee slijtage van een band kan
worden berekend. Dit model is gebaseerd op de theorie van Sueoka [5]. De resultaten
van zijn onderzoek zijn aanleiding voor nieuwe invalshoeken van het cupping
probleem. In samenwerking met bandenfabrikant Vredestein zijn bovendien enkele
suggesties bedacht om het model van Janno Veen te verbeteren en het probleem van
een andere kant te benaderen.
De centrale vraag van dit onderzoek evenals het onderzoek van J. Veen luidt als
volgt: Wat is de oorzaak van onregelmatige bandslijtage en wat kan er aan gedaan
worden om het te voorkomen?
4
1.2
Aanpak van dit onderzoek
In dit verslag wordt in hoofdstuk twee kort uitgelegd hoe het model van J. Veen
werkt. Vervolgens wordt beschreven waarom zijn Lateral Magic Formula vervangen is
door een bandmodel met laterale dynamica en hoe dit bandmodel werkt. Met deze
nieuwe insteek worden enkele tests gedaan en deze worden besproken.
De tweede helft van het onderzoek zoals beschreven in hoofdstuk drie richt
zich op het lokale slijtagemechanisme met behulp van een zogenaamd
‘borstelmodel’. De vraag is of een afgesleten stuk band meer slijt dan een niet
afgesleten stuk. Dit zou onregelmatige slijtage veroorzaken. Eerst wordt de globale
aanpak voor dit probleem besproken. Vervolgens wordt uitgelegd hoe het model
werkt en uiteindelijk zullen de resultaten van dit borstelmodel worden getoond.
In hoofdstuk vier zullen uit de resultaten van de twee onderdelen conclusies
worden getrokken en er zullen aanbevelingen worden gegeven voor verder onderzoek
wat betreft onregelmatige bandslijtage.
5
2
Dynamisch lateraal bandmodel
2.1
Aanpak en beperkingen van het model van J. Veen
Globaal overzicht van het slijtagemodel van J.Veen
De analytische dynamische modellen zijn een manier om meer inzicht te krijgen wat
betreft het onregelmatige slijtagepatroon op banden. Er wordt vooral gekeken naar
hele kleine instabiliteiten in de banddynamica tijdens een steady-state situatie bij
hogere snelheden (denk aan 100 km/u). Als uitgangspunt is het model van het
onderzoek van Janno Veen gebruikt [1]. De opbouw van dit model is weergegeven in
figuur 2.1.
Figuur 2.1: schematisch overzicht van gebruikte modellen van J. Veen
In deze modellen wordt met behulp van een verticaal rigid ring bandmodel en een
band met een onregelmatige straal een normaalkracht berekend. De straal van de
band die wordt ingevoerd is de initiatie. Door deze variaties in hoogte van de band zal
een variatie in de normaalkracht ontstaan. Deze normaalkracht Fz wordt met de
lateral Magic Formula omgerekend naar een spoorkracht Fy, welke de invoer is van
een slijtagewet. De berekende slijtage wordt ten slotte weer opgeteld bij de initiatie
van de band. In dit hoofdstuk wordt uitgelegd hoe enkele onderdelen van het model
van J. Veen werken en wat de beperkingen zijn.
Vertical rigid ring tyre model
Voor een juiste modellering van het gedrag van een band kan het verticale
dynamische gedrag van het hele voertuig worden bekeken. Dit gedrag kan een grote
invloed uitoefenen op de slijtage van de band. Een van de door J. Veen gebruikte
modellen is het ‘vertical rigid ring tyre model’. In figuur 2.2 is een schematisch
overzicht en een free body diagram gegeven van dit model.
6
Figuur 2.2: (a) Schematisch overzicht van het ‘vertical rigid ring tyre model’, (b) Free
body diagram van het model
De verplaatsingen van de as en de gordel van de band zijn respectievelijk
gemodelleerd met Za en Zb met daartussen veren en dempers. Dit bandmodel werkt
met een velg met voorgeschreven verplaatsing en neemt dus de trillingen van het
gehele voertuig niet mee (in tegenstelling tot een kwartvoertuig model). Voor
afleidingen van de bewegingsvergelijkingen en initiële condities zie appendix A. In
Matlab/Simulink heeft J. Veen dit model gekoppeld aan de invoer, namelijk de straal
van de band die continu varieert. Zo kan het verloop van de normaalkracht Fz
berekend worden. In figuur 2.3 is weergegeven hoe Fz varieert bij een simulatie voor
dit model met een enkel klein hoogteverschil op de band als initiatie. Parameters voor
deze simulatie staan in appendix B.1.
7
Figuur 2.3: Variaties in de normaalkracht Fz voor het ‘vertical rigid ring tyre model’
De normaalkracht gedraagt zich bij dit bandmodel als een gedempte sinus die
ontstaat als gevolg van de instantane stap in de initiatie (het kleine hoogteverschil op
de band). De frequentie van deze sinus is de eigenfrequentie van dit systeem en
bedraagt ongeveer 85 Hertz.
Laterale Magic Formula
De ‘Magic Formula’ wordt vaak gebruikt in voertuigdynamica onderzoek. Het is een
betrouwbaar model om de zijdelingse kracht te berekenen. De formule heeft als
invoer de variërende normaalkracht Fz , de camberhoek van het wiel γ en de
sliphoek α en kan dus in deze vorm worden geschreven:
F y = Magicformula (Fz (t ), γ , α )
(2.1)
Het verband is erg complex en voegt weinig toe aan de betrouwbaarheid van het
systeem ten opzichte van een lineaire variant, omdat er alleen kleine verplaatsingen
en verdraaiingen plaatsvinden. Bovendien wordt er geen dynamisch gedrag
gesimuleerd in dwarsrichting en in de verdraaiingen, maar verandert de spoorkracht
instantaan mee met de verticale kracht. Relaxatie-effecten zouden een grote rol
kunnen spelen in dit verband voor de spoorkracht, welke direct verbonden is met
bandslijtage. Om deze redenen is gekozen de Magic Formula te vervangen met een
dynamisch lateraal bandmodel die zijdelingse bewegingen en hoekverdraaiingen van
de band kan simuleren.
8
2.2
Ontwikkeling van het dynamisch lateraal bandmodel
Het dynamische gedrag van een band in zijdelingse richting is belangrijk voor het
simuleren van bandslijtage. De Vries heeft onderzoek gedaan naar de stabiliteit van
motorfietsen [2]. Er wordt aangenomen dat het ‘rigid ring tyre model’ wat bij deze
analyse gebruikt wordt het gedrag van een band goed weergeeft in dwarsrichting en
in de stuur- en camberhoeken. Het gaat hier om de aparte beweging van de velg en
de gordel van de band, welke met elastische verbindingen zijn gemodelleerd. Dit is
dus –voor de duidelijkheid- een rigid ring model in dwarsrichting (out-of-plane
motion), zodat er in feite een rigid ring model gebruikt wordt voor de verticale en
laterale richting. De gelineariseerde bewegingsvergelijkingen van dit model zijn
onder weergegeven (vergelijking 2.2-2.4). Omdat er sprake is van kleine bewegingen
rond een evenwichtspunt voldoet deze gelineariseerde vorm van het model in dit
geval. Een enkel subscript ( x ) geeft een translatie in die richting aan en een dubbel
subscript ( xx ) geeft een rotatie aan. De subscripts a en b staan respectievelijk voor de
velg en de gordel van de band.
I xx γɺɺb = − K xx (γ b − γ a ) − I yy Ωψɺ b − K zz Ω(ψ b −ψ a )
− rFy + ( yb − y a − rγ b )Fz
(2.2)
I zzψɺɺb = I yy Ωγɺb + K xx Ω(γ b − γ a ) − K zz (ψɺ b − ψɺ a ) − C zz (ψ b − ψ a ) + M z
(2.3)
M b ɺyɺb = − K y ( yɺ b − yɺ a ) − C y ( y b − y a ) + Fy
(2.4)
Een overzicht van het coördinatenstelsel en de kracht en momentrichtingen zijn
weergegeven in figuur 2.4.
9
Figuur 2.4: Overzicht van coördinatenstelsel en kracht en momentrichtingen [3]
In vergelijking (2.5) zorgt de relaxatielengte σ c ervoor dat het flexibele
contactoppervlak (die niet in het rigid ring model zit) toch kan worden meegenomen
in het model.
σ cαɺ 1 = rγɺb − aψɺ b + Vψ b − yɺ b − Vα 1
(2.5)
In de bedoelde toepassing van dit model waren Fz, Fy en Mz constanten, terwijl dat
voor deze applicatie niet zo is. De variërende term Fz maakt vergelijking 2.2 nietlineair door de vermenigvuldiging met andere variërende termen. Bovendien hangen
de termen Fy en Mz af van twee variabelen wat ook resulteert in een niet-lineair
verband. Er zijn dus aanpassingen nodig. In vergelijking 2.2 is de laatste niet-lineaire
term een soort knikkracht in de band en deze is erg klein ten opzichte van de andere
termen. Om het model lineair te houden wordt deze term verwaarloosd. Verder zijn
de termen Fy en Mz die afhankelijk zijn van de drifthoek en de normaalkracht Fz in
twee lineaire stukken gesplitst (zie vergelijking 2.6 en 2.7).
10
dC fa


 Fz ( t ) − Fz 0   ⋅ α 0 + αɶ1 ( t ) 
Fy = C fa ( t ) ⋅ α1 ( t ) = C fa 0 +
dFz


(2.6)


dC ma
[Fz (t ) − Fz 0 ] ⋅ [α 0 + α~1 (t )]
M z = C ma (t ) ⋅ α 1 (t ) = C ma 0 +
dFz


(2.7)
De constante waarden in deze formules zijn bepaald voor het werkpunt bij een
normaalkracht van vierduizend Newton en een sliphoek van één graad. De
verschillen met de eerder beschreven laterale Magic Formula zijn minimaal bij kleine
oscillaties rondom het werkpunt. Hiervoor zijn resultaten van krachtmetingen
gebruikt, een van deze plots is weergegeven in figuur 2.5 [3].
Figuur 2.5: linearisatie Fy voor variaties van Fz
De 2e term in Fy neemt dus de kleine variaties van Fz rondom het werkpunt voor zijn
rekening, zie hiervoor vergelijking 2.6.
De vier bewegingsvergelijkingen van dit laterale bandmodel zijn ingevoerd in een
state-space model en is vervolgens ingevoerd in Matlab/Simulink. Ingangen van het
state-space model zijn de hoekverdraaiing en verplaatsingscoördinaten van de velg.
Uitvoer van het model zijn de verplaatsingen en hoekverdraaiingen van de gordel en
sliphoek alfa. Zie appendix E voor het state-space model. Met deze sliphoek kan
vervolgens de spoorkracht Fy berekend worden die bepalend is voor de bandslijtage.
Dit state-space model is geïmplementeerd in het bandslijtage model van J. Veen in de
plaats van de laterale Magic Formula zodat onder dezelfde omstandigheden de
verschillen kunnen worden gesimuleerd. Er is een onderdeel toegevoegd die het
opstartverschijnsel weg filtert, zodat dit niet wordt meegenomen in de slijtage. Dit is
nodig omdat er gekeken wordt naar de slijtage bij stationaire situaties. Voor een
parameterlijst van de gebruikte modellen zie appendix B.
11
2.3
Resultaten van het dynamisch lateraal bandmodel
De eigenschappen van het gelineariseerde dynamisch lateraal bandmodel kunnen
worden bekeken. Een belangrijk detail voor de betrouwbaarheid van de simulatie zijn
de werkpuntswaarden. De werkpuntswaarde voor de verticale kracht is 4000 Newton
en deze is precies het gemiddelde van de responsie in de simulatie. Verder is het nog
van belang dat de sliphoek dicht rondom zijn werkpuntswaarde exciteert. Aangezien
er rekening wordt gehouden met het gedeformeerde contactoppervlak zal de
gebruikte gedeformeerde sliphoek anders zijn dan de stuurhoek van de velg. Om dit
te controleren wordt de gesimuleerde responsie van de gedeformeerde sliphoek α 1
bekeken, zie figuur 2.7.
Figuur 2.7: gesimuleerde responsie van gedeformeerde sliphoek α 1
Zoals te zien in de figuur oscilleert α 1 rond 0.0207 rad of 1.19 graden, wat ongeveer
overeenkomt met de ingestelde hoek ψ a van de velg die de werkpuntswaarde α 0 op
dient te leggen. Hieruit kunnen we concluderen dat de sliphoek en de verticale kracht
dicht bij hun werkpuntswaarden liggen. Het inschakelverschijnsel wordt weg
gefilterd zoals eerder vermeldt.
Nu de gebruikte functie voor Fy gevalideerd is kunnen de systeemeigenschappen
worden bekeken. De overdrachten tussen de in en uitgangen van het systeem kunnen
weergegeven worden met bode-plots. In figuur 2.8 is de overdracht Fz/Fy
weergegeven in een bodediagram.
12
Figuur 2.8: Bodediagram van de overdracht Fy/Fz voor het laterale banddynamica
model
De frequentie waarbij Fz exciteert ligt ongeveer op 85 Hertz. Bij deze frequentie is
een versterking van 0.35 en een fasedraaiing van -328 graden te zien. De
normaalkracht zal de spoorkracht dus niet veel anders beïnvloeden dan een simpele
statische versterking, die eerder ook al gebruikt is. Door de fasedraaiing in dit
systeem zal de onregelmatige bandslijtage wel op een iets andere plek komen.
Aangezien er slechts gekeken wordt naar stationaire situaties zal de verticale kracht
responsie altijd op een bepaalde frequentie liggen, waardoor versterking en
faseverschuiving vastliggen. Als zou worden gekeken naar variaties in deze verticale
krachtfrequenties over de tijd zou dit wellicht wel resulteren in een heel ander
slijtagepatroon.
13
Figuur 2.9: vergelijking tussen slijtage met laterale banddynamica model (a) en
lateral Magic Formula (b)
In figuur 2.9 is het verschil te zien tussen de gesimuleerde slijtage bij het laterale
banddynamica model en bij het model waar de Magic Formula toegepast is, beide in
combinatie met hetzelfde verticale bandmodel en beide met dezelfde
simulatieparameters. De slijtagegroeven zijn inderdaad enkele graden verdraaid ten
opzichte van elkaar zoals verwacht. Wat bovendien opvalt, is het verschil in slijtage
van ongeveer een factor 2. Dit is te verklaren met de hogere versterking die het statespace model geeft aan de relatie tussen verticale kracht en spoorkracht bij de
eigenfrequentie van 85 Hertz. Verder is er een relatief kleine slijtageplek te zien rond
de nul graden bij het dynamisch lateraal bandmodel. Door de kleine faseverschuiving
wordt Fy net voor de initiatiepiek –veroorzaakt door de straalvariatie van de bandlager dan bij het andere model waardoor er extra slijtage optreedt.
14
3
Alternatief slijtagemodel
3.1
Probleem en globale aanpak
Uit de evaluatie van het vrij gecompliceerde lateraal bandmodel met een simpel
slijtage model gaf relatief weinig nieuwe inzichten ten aanzien van onregelmatige
slijtage. In samenwerking met bandenfabrikant Vredestein is er een alternatieve
aanpak naar voren gekomen. De aandacht gaat meer uit van het lokale
slijtagemechanisme in plaats van de dynamica van velg en gordel. In het vorige deel
van dit onderzoek wordt de slijtage gesimuleerd met een puntcontact en een direct
verband tussen dwarskracht en slijtage op dat punt. Het slijtagemechanisme is in
werkelijkheid een stuk complexer. Daarom wordt in dit hoofdstuk getracht meer
inzicht te krijgen in het lokale slijtagemechanisme met een verdeeld contact. Met een
discreet borstelmodel kan lokale slijtage per tijdstap over een heel contactoppervlak
worden gesimuleerd, zie figuur 3.1. De volgende hypothese wordt onderzocht: is het
mogelijk dat een korte borstel sneller slijt dan een lange borstel bij constante
rijsnelheid en sliphoek en veroorzaakt dit onregelmatige bandslijtage?
3.2
Modelvorming
De band wordt gemodelleerd als een platte schijf met elastische borstels. Elke borstel
is in feite een rubberen blokje met een axiale stijfheid en een puntcontact aan de
grond. Elk blokje zit vast aan een vervormde oneindig stijve gordel, welke dus niet
van vorm verandert. De vorm ziet eruit als een afgeplatte parabool. Dit is geoorloofd
omdat alleen stationaire situaties worden bekeken zonder globale krachtvariaties in
verticale richting. De overige invloeden op vervorming van de gordel, zoals
krachtvariatie per blokje van de gordel en zijdelingse vervorming van de gordel
worden verwaarloosd. In figuur 3.1 is een schematische weergave van het model
gegeven. De borstels zijn hier weergegeven als sprieten.
Figuur 3.1: Borstelmodel [3].
15
De band wordt bij een constante snelheid gedwongen een voorgeschreven (constante)
sliphoek α te volgen, waardoor de rubberen blokjes zullen vervormen in dwarsrichting.
De krachtenbalans wordt opgelost en als de dwarskracht groter wordt dan de verticale
kracht maal een wrijvingscoëfficiënt op een blokje zal deze slippen en slijten. De slijtage
per blokje wordt berekend met de verrichte arbeid in de tijdstap maal een constante
slijtagefactor. Na een tijdstap schuiven alle blokjes een plaats op en begint de som
opnieuw. Dit alles wordt in stationaire situatie gesimuleerd in Matlab met discrete
tijdstappen. In appendix C wordt uitgelegd hoe de verschillende delen van het model zijn
opgebouwd. In appendix D is een parameterlijst voor een enkele simulatie weergegeven.
3.3 Resultaten van het borstelmodel
In deze paragraaf wordt besproken wat de resultaten zijn van het borstelmodel. Eerst
wordt gekeken naar een enkele simulatie en zal het onregelmatige slijtage proces
worden uitgelegd aan de hand van de resultaten. Vervolgens wordt gekeken naar
enkele parameterwijzigingen en de invloed daarvan op de slijtage.
Onregelmatige slijtage door verschillende initiële bloklengtes
Om het proces van onregelmatige slijtage uit te leggen worden de resultaten van een
enkele simulatie gebruikt. De gebruikte parameters staan in appendix D. Het verloop
van de verticale kracht Fz en dwarskracht Fy over de x-as op een lang blokje en op een
kort blokje is weergegeven in figuur 3.3.
Figuur 3.3: Krachten voor lang en kort blokje over de x-as
De blokjes lopen in de tijd over de x-as. Doordat de gordelvorm in hoogte varieert
over de x-as is de verticale kracht niet op elke plek hetzelfde. Verder is te zien dat de
verticale kracht voor een korter blokje over de hele tijd lager is dan voor een lang
blokje.
16
De oorzaak hiervan is dat een korter blokje minder wordt ingedrukt, omdat dit blokje
in onbelaste toestand korter is. Verder neemt de dwarskracht evenveel toe in de xrichting voor beide blokjes tot een zeker punt. Vóór dat punt is er sprake van totale
adhesie en geldt er Fy = µ·Fz , met bij deze simulatie µ = 1. Vanaf het punt dat de
dwarskracht hoger wordt dan de verticale kracht zal er dus slip optreden. De
dwarskracht hangt af van de y-positie van het blokje en deze is voor beide blokjes tot
het slippunt hetzelfde. Dit betekent dus dat door de lagere verticale kracht een kort
blokje eerder slipt dan de lange blokjes en dat is te zien in de laatste vier posities van
figuur 3.3
Als er slip optreedt bij een blokje zal deze gaan slijten. In figuur 3.4 is de
slijtage voor een kort en een lang blokje te zien.
Figuur 3.4: Slijtage voor lang en kort blokje over de x-as
Het korte blokje begint dus eerder met slijten dan de lange blokjes. Doordat het korte
blokje eerder slijt beweegt deze niet verder in de y-richting, waardoor de dwarskracht
in de laatste tijdstappen lager is dan voor de lange blokjes. Hierdoor is de instantane
slijtage aan het einde kleiner voor het korte blokje. Het feit dat het korte blokje op
meer posities slijt zal uiteindelijk zorgen voor meer slijtage per omwenteling van het
wiel. Zoals eerder vermeld gaat het niet om de absolute slijtage maar slechts om het
verschil tussen de slijtage van een kort en een lang blokje. Om dit duidelijk weer te
kunnen geven wordt een relatieve slijtage parameter geïntroduceerd:
ξ (t ) =
Totale slijtage van een kort blokje
Gemiddelde totale slijtage van lange blokjes
(3.1)
Na duizend tijdstappen is ξ (t = 1000) = 2.14 , dus heeft het korte blokje meer dan
twee keer zoveel gesleten als een lang blokje.
17
Parameter studie
In de vorige paragraaf wordt voor een enkele simulatie het onregelmatige
slijtagemechanisme uitgelegd. Of dit slijtagemechanisme echt op zal treden is te
betwijfelen, want sommige parameters zijn echter slechts in orde grootte bepaald.
Een parameterstudie zal hier wellicht een beter inzicht geven. Bovendien is het goed
te weten of bij variatie van bepaalde parameters de onregelmatige slijtage toeneemt of
afneemt. Het model van de vorige paragraaf is als uitgangspunt genomen (zie
parameterlijst in appendix D) en vervolgens zullen enkele parameters worden
gevarieerd. Met de relatieve slijtage ratio ξ zullen enkele invloedrijke
parametervariaties worden vergeleken.
Ten eerste wordt gekeken naar variaties in de sliphoek. Tabel 3.1 laat de
verschillende relatieve slijtage ratio zien voor deze parameterwijzigingen. De
dikgedrukte waarde is hetzelfde als de eerder gebruikte waarde.
α [graden] ξ
0.01
inf
0.02
2.14
0.041
1
0.05
0.88
0.1
0.64
1
0.64
10
0.64
Tabel 3.1: Relatieve slijtage ratio voor variaties in sliphoek alfa [graden].
Voor een sliphoek van 0.01 graden gaat de ratio naar oneindig. Dit betekent dus dat
de lange blokjes helemaal niet slijten, terwijl een kort blokje dat wel doet. Verder is te
zien dat vanaf een sliphoek van 0.041 graden en hoger de lange blokjes al meer
slijten dan de korte blokjes. De ratio heeft een limiet van 0.64. Korte blokjes slijten
meer bij kleine sliphoeken, omdat de dwarskracht lager is. Lange en korte blokjes
zullen beide minder slijten op hetzelfde punt, terwijl een kort blokje op meer punten
slijt. De waarden van de sliphoek waarvoor onregelmatige slijtage optreedt, is erg
laag.
De tweede parameter die de slijtage sterk beïnvloedt is de onderlinge afstand tussen
de blokjes. Als deze waarde kleiner wordt zullen er meer blokjes aanwezig zijn in het
contactoppervlak. Tabel 3.2 laat de resultaten zien.
18
dx [mm]
aantal blokjes n ξ
1
200
0.59
3
67
1.09
4
50
2.88
5
40
2.14
7
29
1.8
10
20
1
17
12
1
18
11
Tabel 3.2: Relatieve slijtage ratio voor variaties in onderlinge afstand tussen midden
van de blokjes dx bij een sliphoek van 0.02 graden
Een kort blokje slijt relatief het meeste bij een onderlinge afstand van 4 mm en 50
blokjes. Verder kan opgemerkt worden dat voor lagere en hogere onderlinge
afstanden (meer en minder blokjes) de relatieve slijtage afneemt. Bij een hoog aantal
blokjes slijten lange en korte blokjes op veel posities door de lage verticale krachten.
Korte blokjes slijten nog wel op meer posities, maar lange blokjes slijten harder op
die posities waar ze slijten. Bij 11 blokjes of minder slijten beide blokjes niets meer.
Dit heeft te maken met de hoge verticale krachten per blokje, die zorgen voor een
goede wrijvingskracht in het bandwegcontact waardoor er geen slip en slijtage zal
optreden.
Ten slotte zijn de variaties in de totale verticale kracht die wordt uitgeoefend
op de borstels gevarieerd. De resultaten staan in tabel 3.3.
Fz [N]
ξ
3000
0.92
3500
1.28
4000
2.14
4500
8.03
5000
0.89
Tabel 3.3: Relatieve slijtage ratio voor variaties in totale verticale kracht Fz bij een
sliphoek van 0.02 graden.
De relatieve slijtratio daalt voor lagere verticale krachten, omdat de lange blokjes dan
ook op meer posities zullen slijten. Voor hoge verticale krachten daalt de ratio
uiteindelijk ook, doordat de dwarskracht dan meer toeneemt dan de verticale kracht
waardoor er voor beide blokjes eerder slip en dus slijtage zal optreden. De ratio is
maximaal en opvallend hoog voor een verticale kracht van 4500 Newton. Bij deze
verticale kracht slippen de korte blokjes aanzienlijk meer dan de lange blokjes.
19
4
Conclusies en aanbevelingen
Dit hoofdstuk bevat de belangrijkste conclusies van dit onderzoek en geeft
aanbevelingen voor verder onderzoek ten aanzien van onregelmatige bandslijtage.
Het doel van het onderzoek is het uitbreiden van het onderzoek van Janno Veen in
het beantwoorden van de volgende centrale vraag: Wat is de oorzaak van
onregelmatige bandslijtage en wat kan er aan gedaan worden om het te voorkomen?
4.1
Conclusies
In het door Janno Veen gebruikte bandmodel is de laterale band dynamica niet
meegenomen, want de Lateral Magic Formula die hij gebruikte is slechts een
statische versterking voor kleine variaties in sliphoek tijdens een stationaire situatie.
Het vervangende laterale banddynamica model met een flexibel contactoppervlak
zorgt voor een meer realistische weergave van het dynamische gedrag tussen gordel
en contactoppervlak tussen band en weg. Het model resulteert voor de gebruikte
omstandigheden slechts in een statische versterking met verwaarloosbaar kleine
faseverdraaiing. Het resultaat komt dus globaal overeen met dat van J. Veen. De
versterking in de overdracht tussen verticale en dwarskracht is echter wel een factor
twee hoger, waardoor de band ook twee keer zo snel slijt.
Het borstelmodel dat gebruikt wordt voor een alternatief slijtagemodel laat
zien dat voor kleine sliphoeken en bepaalde omstandigheden de slijtage voor korte
blokjes duidelijk groter is dan voor lange blokjes. Dit leidt uiteindelijk tot
onregelmatige slijtage, doordat een afgesleten stuk band de slijtage op dat stuk
versterkt. Een belangrijke beperking van het model zijn verwaarlozing van verticale
krachtvariaties en gordelvervorming.
20
4.2
Aanbevelingen
De volgende aanbevelingen zijn gemaakt voor meer onderzoek in de toekomst over
onregelmatige bandslijtage.
•
Een relatie zou kunnen worden gelegd tussen de resultaten van het
borstelmodel en een dynamisch model van de ophanging en band. Een model
zou dan een verband kunnen leggen tussen de bandbewegingen en
krachtvariaties op de band en het lokale slijtagemodel dat hier is toegepast.
Met deze krachtvariaties zal het lokale slijtagemechanisme wellicht een heel
ander patroon vertonen.
•
Om meer inzicht te krijgen in de translaties en rotaties van de band in alle
richtingen moeten metingen worden gedaan. Hierbij kan worden gedacht aan
een auto met gecupte banden die met constante snelheid rechtuit rijdt op een
trommel. Men legt een vaste sliphoek op en meet de responsies van translaties
en hoekkantelingen van bandonderdelen. Met deze meetwaarden kunnen
bestaande modellen worden gecontroleerd en verbeterd en kan meer inzicht
worden verkregen over de trillingen in de ophanging.
•
De parameters van het borstelmodel zouden beter gevalideerd moeten worden
zodat er meer inzicht wordt verkregen over de precieze werking van het
slijtagemechanisme en zodat men meer kan zeggen over de betrouwbaarheid
van de absolute resultaten.
•
Een andere verbetering die kan worden gemaakt bij het borstelmodel is de
onderlinge relatie tussen blokjes. Hierbij kan men denken aan een toevoeging
van veer en dempers tussen de verschillende blokjes in longitudinale richting,
zodat de blokjes elkaar sterker beïnvloeden.
•
Bovendien kan worden nagedacht over de slijtage op andere posities van de
band. Tot nu toe zijn er alleen modellen gebruikt met één positie in de breedte
van de band. Het is denkbaar dat een band onder een sliphoek in een bepaalde
richting slijt die niet gelijk is aan de gebruikte assen en wellicht treedt er meer
onregelmatige slijtage op bij bepaalde posities in de breedte van de band.
21
Referenties
[1]
Veen, J., “An analytical approach to dynamic irregular tyre wear”, DCT
2007.093
[2]
De Vries, E.J.H. en Pacejka, H.B., “The effect of tire modeling on the stability
analysis of a motorcycle,” Delft University of Technology.
[3]
Besselink, I.J.M., “Vehicle Dynamics 4L150”, dictaat van vak 4L150 TU
Eindhoven, 2005-200.
[4]
Lupker, H., Cheli, F., Braghin, F., Gelosa, E. en Keckman, A., “Numerical
Prediction of Car Tyre Wear Phenomena and Comparison of the Obtained
Results with full-Scale Experimental Tests”, Tire Society meeting, 2003, pp 1418.
[5]
Sueoka, A., Ryu, T., Konou , T., Togashi, M. and Fujimoto, T.,
“PolygonalWear of Automobile Tire,’ JSME International journal series C,
Vol. 40, No.2, Juni 1997, pp. 209-217, ISSN 1344-7653
22
Symbolenlijst
α
α0
α1
α~1
γ
γb
γa
ψb
ψa
ξ
µ
σc
Sliphoek
[rad]
Werkpuntswaarde voor sliphoek
[rad]
Gedeformeerde sliphoek
[rad]
Variaties rondom werkpunt van gedeformeerde sliphoek [rad]
Kantelhoek
[rad]
Kantelhoek van de gordel
[rad]
Kantelhoek van de velg
[rad]
Stuurhoek van de gordel
[rad]
Ω
A
C fa
Stuurhoek van de velg
Relatieve slijtage parameter
Rolweerstand coëfficiënt
Relaxatielengte
Omwentelingssnelheid van het wiel
Effectief contactoppervlak van de band
Constante voor lineair verband tussen Fy en α
[rad]
[-]
[-]
[m]
[rad/s]
[ m2 ]
[N/rad]
C fa 0
Werkpuntswaarde voor lineair verband Fy ~ α 1
[N/rad]
dC fa / dFz
Werkpuntswaarde voor lineair verband Fy ~ Fz
[1/rad]
C ma 0
dC ma / dFz
Werkpuntswaarde voor lineair verband M z ~ α 1
Werkpuntswaarde voor lineair verband M z ~ Fz
[Nm/rad]
[m/rad]
Cy
Laterale stijfheid van één blokje
[N/m]
Cz
C z −totaal
C zz
dh gordel
dx
E
Fy
Verticale stijfheid van één blokje
Totale verticale stijfheid van alle blokjes
Torsie zijdelingse stijfheid rond z-as
Variërende hoogte van de gordel t.o.v. het midden
Onderlinge afstand tussen midden blokjes in x-richting
Elasticiteitsmodulus van rubber
Dwarskracht op blokje
[N/m]
[N/m]
[N/rad]
[m]
[m]
[Pa]
[N]
Fy − noslip
Dwarskracht op blokje voor oneindige rolweerstand
[N]
Fy −totaal
Totale dwarskracht op alle blokjes
[N]
Fz
Fz 0
Fz −totaal
i
I xx
Verticale kracht
Werkpuntswaarde verticale kracht
[N]
[N]
Totale verticale kracht op alle blokjes
Teller van het blokje
Traagheidsmoment van de gordel rond x-as
[N]
[-]
[kg m 2 ]
23
I yy
Traagheidsmoment van de gordel rond y-as
[kg m 2 ]
I zz
k1
k2
K xx
Ky
Traagheidsmoment van de gordel rond z-as
Slijtageparameter 1
Slijtageparameter 2
Torsie zijdelingse demping rond x-as
[kg m 2 ]
[1/N]
[-]
[Nm/rad]
Laterale demping
[Ns/m]
K zz
l0
Mb
Mz
n
r
slipweg
t
V
W
y
y noslip
Torsie zijdelingse demping rond z-as
Initiële lengte van een lang blokje
Massa van de gordel
[Nm/rad]
[m]
[Kg]
Zelf instellend moment van de band
Aantal rubberen blokjes
Effectieve straal van het wiel
Geslipte afstand van blokje gedurende een tijdsstap
Teller van de tijdsstap
Longitudinale snelheid van het voertuig
Verrichte arbeid per blokje gedurende een tijdsstap
Daadwerkelijke positie van een blokje op y-as
Positie van blokje op y-as voor oneindige rolweerstand
[Nm]
[-]
[m]
[m]
[-]
[m/s]
[Nm]
[m]
[m]
Za
Verplaatsing van de velg over de y-as
Verplaatsing van de gordel over de y-as
Verticale verplaatsing van de as
[m]
[m]
[m]
Zb
Verticale verplaatsing van de gordel
[m]
ya
yb
24
A
Bewegingsvergelijkingen van het verticale starre
ring bandmodel
Het verticale bandmodel is een dynamisch model voor de krachten en verplaatsingen
tussen de weg, de as en de gordel van een band. Het gebruikte model benadert de
werkelijkheid met twee voorgeschreven randvoorwaarden. De gordelmassa mb hangt
tussen de velg en de weg in met veren en dempers. De schematische weergave van
het model is zichtbaar in figuur 2.2a. De verplaatsingen van de velg, de gordel en de
dikte van het loopvlak van de band zijn respectievelijk gemodelleerd met Z a , Z b en
U (t − T ) met daartussen veren en dempers die zich als de ophanging gedragen. De
volgende krachtbalansen kunnen voor het bandmodel worden afgeleid:
Fz (t ) = c r (U (t − T ) − Z b (t ))
F (t ) = k ⋅ Zɺ (t ) + c (Z (t ) − Z
b
b
b
b
b
(A.1)
a0
)
(A.2)
In bovenstaande vergelijkingen is Fz de normaalkracht die op de weg werkt en Fb de
kracht werkend tussen de riem en de as van het wiel. Deze vergelijkingen worden
gebruikt om de bewegingsvergelijking van de gordel af te leiden.
mb Zɺɺb (t ) + k b ⋅ Zɺ b (t ) + cb (Z b (t ) − Z a 0 ) + c r (Z b (t ) − U (t − T )) + mb g = 0
(A.4)
De initiële conditie Fz 0 is bepaald door de som van de zwaartekracht van de gordel
met de constante kracht Fl 0 , die veroorzaakt wordt door de onafgeveerde en
afgeveerde massa van de auto.
Fz 0 = Fl 0 + mb ⋅ g
(A.5)
De initiële verplaatsingen worden afgeleid uit de bewegingsvergelijkingen in
stationaire situatie. Er is geen dynamische onregelmatige bandslijtage in stationaire
situatie, omdat er geen krachtvariaties zijn. Om deze reden is de waarde U 0 (t − T )
nul verondersteld.
Fl 0 + mb ⋅ g
cr
F + mb ⋅ g Fl 0
= − l0
−
cr
cb
Z b0 = −
(A.6)
Z a0
(A.7)
25
B.1 Parameterlijst van het model van J. Veen
Parameter Waarde
Eenheid Beschrijving
Vx
112 [km/u]
Voorwaartse snelheid
tmax
100 [s]
simulatie tijd
mb
4.6 [Kg]
gordelmassa
cr
2.99E+05 [N/m]
Residuele stijfheid
cb
0.941 [N/m]
zijdelingse stijfheid
kb
147 [Ns/m] zijdelingse demping
ms
383 [Kg]
afgeveerde massa
v
1.09E-12 [m/N]
slijtage weerstand factor
alfa
1 [deg]
sliphoek
gamma
0 [deg]
camberhoek
n
1 [-]
nth power van slijtage
r
0.3 [m]
Straal van het wiel
g
9.81 [m/s^2] gravitatie
Table B.1: Parameterlijst van het model van J. Veen
26
B.2 Parameterlijst van het dynamisch lateraal
bandmodel
Parameter
Ky
Cy
Cxx
Czz
Kxx
Kzz
Ixx
Iyy
Izz
oc
Waarde
100
800000
25500
25500
4
4
0.326
0.633
0.326
0.25
Eenheid
[Ns/m]
[N/m]
[N/rad]
[N/rad]
[Ns/rad]
[Ns/rad]
[Kg m^2]
[Kg m^2]
[Kg m^2]
[m]
Beschrijving
residuele zijdelingse demping
residuele zijdelingse stijfheid
zijdelinge torsiestijfheid rond x-as
zijdelinge torsiestijfheid rond z-as
zijdelinge torsiedemping rond x-as
zijdelinge torsiedemping rond z-as
traagheidsmoment rond x-as
traagheidsmoment rond y-as
traagheidsmoment rond z-as
relaxatielengte in werkpunt
halve bandcontactlengte in
a
0.1 [m]
werkpunt
Fz0
4000 [N]
totale verticale kracht in werkpunt
alfa0
1 [deg]
sliphoek in werkpunt
constante voor Fy bepaling rond
Cfa0
1250 [N/rad]
werkpunt
constante voor Mz bepaling rond
Cma0
45 [Nm/rad] werkpunt
constante voor Fy bepaling rond
dCfa/dFz
0.15 [1/rad]
werkpunt
constante voor Mz bepaling rond
dCma/dFz
0.01 [m/rad]
werkpunt
gamma_a0
0 [rad]
camberhoek van velg
gamma_at0
0 [rad/s]
camberhoeksnelheid van velg
psi_a0
0 [rad]
stuurhoek van velg
psi_at0
0 [rad/s]
stuurhoeksnelheid van velg
y_a0
0 [m]
translatie van velg over y-as
y_at0
0 [m/s]
snelheid van velg over y-as
Table B.2: parameterlijst van dynamisch lateraal bandmodel
27
C
Implementatie van het borstelmodel
Het tweede deel van dit onderzoek is gebaseerd op een discreet borstelmodel,
geprogrammeerd in Matlab. De achtergrond van dit model is gebaseerd op een
borstelmodel uit het collegedictaat van het vak ‘Vehicle Dynamics’ aan de Technische
Universiteit Eindhoven [3]. Ideeën over implementatie van het slip- en het
slijtagemechanisme zijn deels afkomstig van Hans van Benthem, werknemer bij
bandenfabrikant Vredestein. Hieronder wordt kort uitgelegd hoe de belangrijkste
onderdelen van de Matlab-file werken.
Axiale stijfheid per blokje
Er wordt uitgegaan van een constant contactoppervlak tussen band en weg. Er wordt
uitgegaan van een effectief contactoppervlak van 0.1 bij 0.15 meter met de weg, dus
de groeven van de band zitten hier niet bij. Het aantal rubberen blokjes n hangt af
van de contactlengte xtotaal en de onderlinge afstand tussen midden van de blokjes dx.
n=
xtotaal
dx
(3.1)
Vervolgens kan worden berekend wat de totale verticale stijfheid van het rubberen
blokje is. De axiale stijfheid per blokje C z wordt uiteindelijk als volgt afgeleid:
Cz =
C z −totaal E ⋅ A
=
n
n ⋅ l0
(3.2)
Vorm van de gordel
De vorm van de gordel is bepalend voor de krachtverdeling op de blokjes in verticale
richting. De vorm zal dus ook invloed hebben op de slijtage.
Omdat er slechts gekeken wordt naar stationaire situaties wordt er uitgegaan van een
constante (vervormde) gordelvorm. De gordel wordt oneindig stijf veronderstelt en
heeft de vorm van een afgeplatte parabool. De kromming van de parabool wordt
aangepast aan de parameters zodat de buitenste blokjes nog net de grond raken in
belaste toestand. Aangezien de buitenste blokjes het minste worden ingedrukt raken
alle gebruikte blokjes dus de weg.
Verticale en dwarskrachten
De blokjes worden samen belast met een totale kracht van 4000 Newton in verticale
richting. Deze kracht wordt verdeeld over de blokjes met een stijfheid berekening,
waarin de variërende hoogte van de gordel dh gordel in acht wordt genomen.
De totale dwarskracht op het contactoppervlak is een empirisch gefitte functie van de
sliphoek en totale verticale kracht.
28
Fy −totaal = C fα (Fz −totaal ) ⋅ α
(3.3)
De dwarskracht per blokje wordt bepaald met een dwarsstijfheid C y (t ) die afhangt
van y noslip (t , i ) . Dit is de y-positie van een blokje i op tijdstip t voor oneindige
weerstandcoëfficient ( µ = inf ).
C y (t ) =
Fy −totaal
(3.4)
mean( y noslip (t , i ))
Fy − noslip (t , i ) = C y (t ) ⋅ y noslip (t , i )
(3.5)
Slip
Per tijdsstap wordt aan de hand van een krachtenevenwicht bepaald of een blokje
slipt of niet. De maximale wrijvingskracht die het bandwegcontact kan leveren is
gelijk aan wrijvingscoëfficiënt µ maal verticale kracht Fz . Als de dwarskracht Fy − noslip
van een blokje groter wordt dan deze wrijvingskracht betekent dit dat blokje i slipt op
tijdstip t.
Als een blokje niet slipt dan is de positie y (t , i ) hetzelfde als y noslip (t , i ) en zal er geen
slijtage optreden. Slipt een blokje wel dan wordt de positie bepaald met de maximale
adhesiekracht en de dwarsstijfheid:
y (t , i ) =
Fy (t , i )
=
µ ⋅ Fz (t , i )
(3.6)
C y (t )
C y (t )
In theorie zal de blokje evenveel slippen als het verschil tussen y-positie bij geen slip
en bij slip. Dus geldt het volgende verband:
slipweg (t , i ) = y noslip (t , i ) − y (t , i )
(3.7)
Voor de duidelijkheid is in figuur 3.2 een bovenaanzicht van de posities per blokje
weergegeven.
Figuur 3.2: Bovenaanzicht blokje posities
29
Slijtage
Nu de slip bekend is kan een slijtagemodel worden toegevoegd aan het model. De
lokale slijtage van een blokje wordt vaak gemodelleerd als een functie van het
vermogen [4].
slijtage = k1 ⋅ W k 2
(3.8)
Met W het vermogen en k1 en k 2 constanten die bij bepaalde omstandigheden het
slijtagegedrag voor rubber karakteriseren. De waarden hiervan zijn niet zo belangrijk
voor dit onderzoek, omdat slechts aangetoond hoeft te worden dat kleinere blokjes
relatief meer slijten dan lange blokjes en niet hoeveel ze absoluut meer slijten.
Aangezien we in dit model rekenen met discrete tijdstapjes kan er gerekend worden
met verrichte arbeid in plaats van vermogen. De constanten k1 en k 2 zullen dan wel
een andere waarde en betekenis hebben maar dat is zoals eerder vermeld hier niet
van belang. De verrichte arbeid per blokje gedurende een tijdsstap wordt als volgt
berekend:
W (i ) =
( F ( t , i ) − F ( t − 1, i − 1) ) ⋅ slipweg
y
y
(3.9)
2
Voor de volgende tijdsstap wordt de nieuwe lengte en positie van elke blokje bepaald
door de slijtage er af te trekken en de krachtenbalans overnieuw uit te rekenen.
y noslip (t , i ) = y (t − 1, i − 1) + dx ⋅ α
(3.10)
Het blokje schuift elke tijdstap een stukje meer naar buiten over de y-as door de
sliphoek alfa die is opgelegd. Dit wordt berekend in verband (3.10). Het achterste
blokje sluit de volgende tijdsstap weer voor aan.
30
D
Parameterlijst van het borstelmodel
Parameter Waarde
Eenheid
Fz_totaal
4000 [N]
alfa
0.02 [deg]
mu
1 [-]
a
1E-08 [1/N]
b
1 [-]
E
1E+07 [Pa]
b_eff
0.1 [m]
x_totaal
0.2 [m]
l_eff
0.15 [m]
l0_kort
0.99E-03 [m]
l0
1E-03 [m]
Beschrijving
Totale verticale kracht op blokjes
sliphoek
wrijvingscoëfficient in slipbepaling
slijtage parameter 1
slijtage parameter 2
Elasticiteitsmodulus van rubber
Effectieve breedte van contactoppervlak
Totale lengte van contactoppervlak
Effectieve lengte van contactoppervlak
lengte kort blokje
lengte normaal blokje
onderlinge afstand tussen middens van blokjes in xdx
5E-03 [m]
richting
t_eind
1000 [-]
Aantal tijdsstappen voor simulatie
Tabel D.1: Parameterlijst van het borstelmodel
31
E
State-space vorm van het dynamisch lateraal
bandmodel
De vier bewegingsvergelijkingen van het dynamisch lateraal bandmodel zijn ingevoerd in
een state-space model. De verticale kracht Fz is een invoer van dit model. Deze kracht is
gelijk aan de normaalkracht van het tyre model of het quarter car model. De overige
ingangen bepalen simpelweg de stand en verplaatsingssnelheden van de velg en de
afgeleiden van deze stand naar de tijd worden nul gekozen. In Appendix B2 is een lijst
weergegeven met de gebruikte parameters. Het state-space model is als volgt
gedefinieerd:
xɺ = A ⋅ x + B ⋅ u
y = C ⋅ x + D ⋅u
en
Toestand
x = [γɺb ,ψɺ b , yɺ b , γ b ,ψ b , y b , α 1 ]
Invoer
u = [Fz , γɺ a ,ψɺ a , yɺ a , γ a ,ψ a , y a ]
Uitvoer
 K xx

 I xx
 I yy ⋅ ω

 I zz

 0
A=

 1
 0

 0
 r

 oc
(2.7)
T
(2.8)
T
[
y = Fy , γ b ,ψ b , y b , α 1
− I yy ⋅ ω
I xx
− K zz
I zz
0
0
1
0
−a
oc
(2.9)
]
T
(2.10)
0
−C xx
I xx
− K zz ⋅ ω
I xx
0
0
K xx⋅ω
I zz
−C zz
I zz
0
0
0
0
0
0
0
0
0
V
oc
−K y
Mb
0
0
1
−1
oc
0
32
−C y
Mb
0
0
0
0
− r ⋅ C fa 0 

I xx 
Cma 0 

I zz 
C fa 0 

Mb 

0


0

0

−V 

oc 
 dCma ⋅ α 0
 dF ⋅ I
z
zz

 dCma ⋅ α 0

 dFz ⋅ I zz
 dC fa ⋅ α 0
B=
 dFz ⋅ M b

0

0


0


0

0

0
C = 0

0
0

0
K zz
I zz
0
− K xx ⋅ ω
I zz
C zz
I zz
0
K zz
I zz
0
− K xx ⋅ ω
I zz
C zz
I zz
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
Ky
Mb
0 0 0 0 0 C fa 0 

0 0 1 0 0
0 
0 0 0 1 0
0 

0 0 0 0 1
0 
0 0 0 0 0
1 
 dC fa ⋅ α 0

 dFz

0
D=
0


0

0


0 0 0 0 0 0

0 0 0 0 0 0

0 0 0 0 0 0
0 0 0 0 0 0

0 0 0 0 0 0 
33

0 


0 

Cy 

Mb 
0 

0 
0 

0 