Natuurkunde 12 module D, E , I

EXTRA VIII
ELEKTROMAGNETISME
2016-17 BTn
NATUURKUNDE 6 VWO
Eerst 6 wat simpeler sommen, waarvan de antwoorden in de PPT ELEKTROMAGNETISME staan. Dan 9 oude VWO-examensommen, met antwoorden.
1 EM KANON
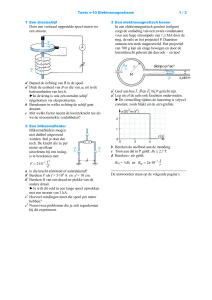
In een elektromagnetisch geschut springt er
een vonk over van P naar Q, daarbij zorgt de
‘spoel’ APQB voor een B-veld het papier in
(de kruisjes). Het gevolg is dat de vonk naar
rechts beweegt en het projectiel van 0,30 kg
meeneemt.
A Leg uit wat de pluspool is, A of B (Hint: RHR spoel gebruiken!)
B Toon aan dat de vonk naar rechts beweegt (Hint: LHR-kracht gebruiken).
Aan het eind van de loop na 0,005 s heeft het projectiel een snelheid van 600 m/s.
C Bereken de lengte van de loop (hint: uit de gemiddelde snelheid).
D Bereken uit de versnelling de gemiddelde kracht op het projectiel.
2 BOOTJE
Dit bootje dat in zout water drijft zou in principe
moeten gaan varen, door zich af te zetten op de
ionenstroom in het water. Via beide elektroden
loopt er stroom tussen de polen van de magneet.
A Waarom kan zo’n bootje in zoet water ook in
theorie niet varen?
B Leg uit of de noordpool onder of boven zit.
Het water heeft een weerstand van 25 Ohm per cm. De afstand tussen de elektroden is 20
cm. De spanning van de accu 12 V en de sterkte van het magneetveld 0,01 T.
C Bereken de grootte van de Lorentzkracht die je hiermee krijgt.
3 KARRETJE
Een karretje waarop een hoefijzer magneet is gemonteerd beweegt langs een spoel die
met een oscilloscoop verbonden is. Bij passeren van de spoel verschijnen in het beeld
van de oscilloscoop twee pieken (zie figuur, voor de getallen).
A Waarom zijn de twee pulsen tegengesteld?
B Waarom is het oppervlak van de pulsen even groot?
C Leg uit of de beweging versneld was, dan wel vertraagd of eenparig.
D Bereken de gemiddelde snelheid karretje?
E Welk beeld verschijnt er op de oscilloscoop als de magneet een halve slag draait.
4
VALLENDE MAGNEET
Een magneet valt door een plexiglazen buis omlaag, om de buis
Is een spoel geslagen, die op de aangegeven manier verbonden
is met een rood en een groen LEDje. Aan de onderkant van de
magneet zit een noordpool. Door de LEDjes kan alleen stroom
lopen in de doorlaatrichting (pijl), dan geven de LEDjes licht.
A
Leg met behulp van de wet van Lenz uit in welke volgorde
De LEDjes flitsen.
B
Beredeneer in welke volgorde de LEDjes flitsen als de buis
wordt omgedraaid en de magneet opnieuw omlaag valt, nu met
de zuidpool omlaag.
5
SLINGERENDE SPOEL
Een spoel slingert van rechts naar links over een sterke magneet. Op deze spoel zijn een
rode (R) en een groene (G) LED parallel aangesloten.
A Beredeneer in welke volgorde de LEDs zullen oplichten. Leg hierbij al je tussenstappen
heel precies uit!
B Leg ook uit hoe die volgorde is bij de volgende passage van de magneet.
6
SPOORRAILS
Van onder naar boven wijst een extern B-veld. Een asje wordt met 2,0 m/s naar rechts
getrokken, terwijl het geleidend verbonden is met twee metalen die door een 0,40 Ohms
weerstand zijn verbonden.
A Hoeveel spanning staat er over de weerstand als B = 0,020 (T)?
B Wat is er gestileerd, theoretisch, aan deze opgave?
A DE ONTDEKKING VAN HET ELEKTRON
Rond 1900 ontdekte JJ Thomson het elektron.
In een vacuüm buis deed hij experimenten met
kathodestralen: na ze met de bronspanning V KA
kathodestralen te hebben gemaakt boog JJ ze
af door een elektrisch veld E tussen de platen
A en B aan te leggen. Bij het positief maken
van B werden de kathodestralen omlaag
getrokken. Het zou dus kunnen gaan om
negatieve deeltjes met massa me, lading e en
snelheid v. Uit een energieomzetting leidde
Thomson af dat dan geldt:
e
v2
.

m 2V AK
A
Leidt deze formule af uit de energieomzetting voor het lanceren van elektronen.
De snelheid in deze formule is geen waarneembare grootheid. Om deze weg te krijgen
kreeg JJ het idee om tussen A en B ook nog een magnetisch veld aan te leggen dat zo
groot is dat de lorentzkracht de elektrische kracht precies opheft, zodat de elektronen
recht door gaan. Dit bleek de sleutel tot de oplossing.
B
Hoe moet het magneet veld tussen A en B dan gericht zijn en hoe kun je zo´n B-veld
handig maken?
C
Laat zien dat uit het feit dat tussen A en B bij rechtoor gaande elektronen met
snelheid v, massa me en lading e omdat daar de Lorentz- en de elektrische kracht el-kaar
opheffen volgt dat de snelheid gelijk is aan
E
v .
B
Combineren van deze vergelijkingen leverde Thomson voor de lading-massa verhouding
van elektronen op dat
e
E2
.

m 2 B 2V AK
D
Leidt deze regel af uit twee eerdere vergelijkingen.
Thomson had een magneet van 0,50 T en versnelde zijn elektronen over een spanning
VAK=0,800 (kV). Het elektrisch veld tussen A en B bedroeg E = 8,4x106 (V/m).
E
Bereken de lading-massa verhouding die Thomson voor elektronen vond.
Thomson vergeleek zijn resultaat met de lading-massa verhouding van het waterstof-ion,
dat bekend was uit elektrolyse experimenten.
F
Bereken die verhouding uit de gegevens in BINAS.
G
Wat concludeerde Thomson uit de vergelijking van zijn resultaten bij E en F?
B PROEF VAN MILLIKAN
Robert Andrew Millikan heeft in ‘n eindeloze reeks
experimenten aangetoond dat lading in de natuur
gequantiseerd is. Van 1896 tot en met 1913 heeft
hij zijn beroemde oliedruppel experimenten gedaan
die hem uiteindelijk in 1923 de Nobelprijs opleverde.
Hij liet minuscule oliedruppels tussen platen van
een condensator omlaag vallen om te bepalen hoe
groot de druppels zijn en vervolgens ging hij de
lading op die druppels meten door te kijken hoeveel
volt er nodig is om de druppels stil te hangen. Een
van zijn druppels had een tijd van 27,4 s nodig om
de afstand va 1,000 mm eenparig af te leggen.
Oliedruppels met straal r en snelheid v ondervinden een wrijvingskracht volgens Stokes’
formule
Fw  6rv ,
-5
hier is η = 1,80x10 (Ns/m2) de viscositeit van lucht. De druppels worden geacht bolvormig
te zijn, zodat er geldt
V  43 r 3
A
Toon met een krachtenanalyse voor een vallend druppeltje aan dat de snelheid van
het druppeltje gegeven wordt door
2 r 2 g
,
v
9
met ρ = 800 (kg/m3) de dichtheid van de olie waar het druppeltje uit bestaat.
B
Toon aan dat de massa van deze oliedruppel 7,8x10-16 kg is.
Er wordt spanning over de condensatorplaten gezet. Hierdoor ontstaat een omhoog
gericht elektrisch veld E = 23,7x103 (V/m). Bij deze veldsterkte blijft het druppeltje
stilhangen.
C
Is het druppeltje positief of negatief geladen?
D
Hoeveel elementair ladingen bevat de druppel?
C LORENTZKRACHT
Op een paar horizontale rails rijdt een karretje van 20,0 gram. Via een koord dat over een
katrol is geslagen wordt ‘t karretje voortgetrokken door een zakkend gewichtje. Er treedt
nergens wrijving op.
A
Bereken de versnelling die het systeem van karretje en massa krijgt als er geen
inductie stroom zou gaan lopen.
Er is een vertikaal homogeen magneetveld aanwezig. Er gaat wel een inductiestroom
lopen. Omdat het achterste asje van het karretje geleidend is vormen weerstand R, de
rails en het asje een circuit waarin elektrisch vermogen ontwikkeld en verbruikt wordt. Op
het geheel staat een magneetveld van 0,50 T. De afstand tussen de rails is 4,8 cm. Het
systeem gaat met constante snelheid v bewegen.
B
Leg uit in welke richting de inductiestroom loopt.
C
Bereken de grootte van de inductiestroom.
D
Leg uit waarom de snelheid constant wordt.
E
Bereken die snelheid als R = 0,020 Ohm.
D
PROEVEN MET ZUUR
In een schaaltje bevindt zich water met wat zuur.
De oplossing bestaat uit 1-waardige ionen, er zijn
dus evenveel positieve als negatieve ionen. Rand R
van het schaaltje is van metaal, de bodem van glas.
In het midden van het schaaltje staat een metalen
stift S. We sluiten R en S aan op ’n gelijkspanningsbron van 20 V. Er gaat dan 0,50 A lopen.
A
Geef in de figuur hieronder aan in welke richting de getekende ionen gaan bewegen.
B
Bereken hoeveel elektronen er per sec door de
ampèremeter lopen.
C
Bereken hoeveel joule er in 10 sec aan warmte
in de vloeistof ontwikkeld wordt (Hint: alleen deze
vloeistof heeft weerstand, de draden niet).
We plaatsen het bakje nu op een elektromagneet en
sluiten het bakje en de elektromagneet op dezelfde
spanningsbron G aan. De sterkte van het B-veld is in
verticale richting 1,0 T. De ampèremeter wijst weer
0,50 A aan. De vloeistof blijkt te gaan roteren met S
als middelpunt.
D
Welke kracht is hier voor verantwoordelijk?
E
Bereken de grootte van die kracht op een ion dat
met een (gemiddelde) snelheid van 1,0x10-4 (m/s) in de
richting van S beweegt.
F
Leg uit in welke richting de vloeistof gaat bewegen.
Geef de draairichting in de figuur hierboven aan, doe zit
voor zowel positieve als negatieve ionen.
Om de rotatie in de klas zichtbaar te maken, laten we ‘n paar kaarsjes op de vloeistof
drijven. Voor een goed effect blijkt ‘t nodig wat extra zuur aan de oplossing toe te voegen.
G
Leg uit waarom dat zo is.
H
Leg uit of de vloeistof wel of niet gaat roteren als we G wisselspanning geven.
E
SLINGERENDE SPOEL
Aan slinger van 1,60 m hangt een spoel met een weekijzeren kern. De uiteinden P en Q
van de slinger zijn niet verbonden. We laten de slinger een hoek van 60o met de vertikaal
maken alvorens los te laten. Bij deze hoek geldt de normale slingerformule van Huygens
bij benadering.
A
Bereken hoeveel sec na ´t loslaten van de slinger
de evenwichtsstand gepasseerd wordt.
B
Bereken de snelheid waarmee de evenwichtstand
gepasseerd wordt (Hint: energiebeschouwing!).
Onder de evenwichtsstand plaatsen we vervolgens een
sterke magneet, waarvan de noordpool boven zit. De
weekijzeren kern ondervindt hiervan een kracht.
C
Leg zowel voordat als nadat de evenwichtsstand
gepasseerd wordt uit of deze kracht aantrekkend dan
wel afstotend is.
P en Q worden met elkaar verbonden door op de spoel een lampje te plaatsen. We laten
de slinger weer bij een hoek van 60o los. Telkens als de spoel langs de magneet beweegt
licht het lampje even op.
D
Leg uit hoe dat komt.
Na een tijdje heen en weer slingeren neemt de snelheid
waarmee de evenwichtsstand gepasseerd wordt af.
E
Leg uit waarom het lampje dan minder fel brandt.
De spoel met kern ondervindt door het aanbrengen van het
lampje een extra kracht van de magneet.
F
Leg zowel voor- als nadat de evenwichtsstand gepasseerd wordt uit of de extra kracht aantrekkend of afstotend is en
welke pool onder zit bij de spoel.
Het verloop van de lichtsterkte van het lampje is als functie van de tijd gegeven. De grafiek
hierboven geeft het resultaat. Op de tijdas komt 1 hokje overeen met 0,20 s.
G
Bepaal de trillingstijd van de slingerbeweging
met behulp van de grafiek.
H
Leg uit waarom bij het passeren van de
evenwichtsstand een relatief minimum R van de
lichtintensiteit hoort.
De stroom noemen we positief als van P via het
lampje naar Q loopt.
I
Schets hiernaast de stroomsterkte door het
lampje bij het passeren van de evenwichtstand als
functie van de tijd en leg uit waarom je deze keuze
hebt gemaakt.
F
INDUCTIESTROMEN
Om een weekijzeren U-kern worden twee spoelen
van elk 375 windingen geplaatst. Bovenop deze Ukern zijn 2 stukken weekijzer bevestigd, zodat er
tussen beide stukken een smalle luchtspleet ontstaat. Hiernaast zie je een perspectieftekening
van de opstelling.
Op de volgende pagina is een doorsnede van
de opstelling getekend, compleet met het magneetveld dat door de spoelen wordt veroorzaakt. Beide
spoelen worden in serie aan gesloten op een gelijkspanningsbron.
A
Teken in die figuur hoe de spoelen met elkaar en
met de bron verbonden moeten worden, zodat ‘t
getekende B-veld ontstaat. Geef ook de stoom aan.
Voor de sterkte van het B-veld in de luchtspleet
van de afgebeelde magneet geldt bij benadering
 .N .I
B  0,27 0
d
waarin
μ0 permeabiliteit vacuüm (BINAS 7),
N het aantal windingen om de kern,
I de stroomsterkte (A) en
d de spleetbreedte (m).
B
Bereken de sterkte van het magneetveld in
de spleet als I = 5,0 (A) en d = 0,0070 (m).
Een katrol is voor de helft in de luchtspleet geplaatst. De
katrol is gemaakt van plexiglas, waarin een viertal gesloten
lussen van koperdraad zijn geplaatst. Een tweede katrol
bevindt zich verticaal boven de eerste. Over de katrollen
loopt een koord, waaraan een blokje is bevestigd. Als je
het blokje vanuit de hoogste positie loslaat komt het in
beweging. De katrollen ondervinden geen wrijving bij het draaien en het koord slipt niet
tijdens de beweging. Als er geen stroom in de spoelen loopt is de beweging van het blokje
eenparig versneld.
Als er wel stroom door de spoelen loopt
wordt de beweging van ‘t blokje al snel eenparig. Hiernaast is een momentopname van de
onderste katrol te zien, tijdens het bewegen
bij een ingeschakeld magneetveld. Het B-veld
is naar voren gericht (punt = naar voren). De
lussen zijn genummerd.
C
Geef in de figuur hiernaast aan in welke
lussen (inductie)stroom loopt door de richting
van die stroom aan te geven. Leg daarnaast uit
waarom de stroom die richting heeft.
D
Geef in die figuur ook aan wat de richting
is van de lorentzkracht op de lussen. Licht ook
hier je antwoord toe.
E
Beredeneer waarom de beweging eenparig wordt.
De sterkte van het magneetveld is B=0,36 (T). Tijdens de eenparige beweging schuift de
lus in 0,085 s helemaal het B-veld in. De weerstand van een lus is R = 9,3x10-4 ( Ώ) en de
oppervlakte van een lus is A = 2,0x10-4 (m2) .
F
Bereken de stroomsterkte in die lus.
G
VERSTROOING VAN ELEKTRONEN
Uit bron B komen elektronen die allemaal dezelfde energie hebben. Ze komen in ruimte I,
waarin zich uitsluitend kwikdamp onder zeer lage druk bevindt. Sommige elektronen
botsen tegen de kwikatomen, een proces waarbij energie van de elektronen op de
kwikatomen kan worden overgedragen. Wanneer de elektronen bij de botsingen een
geschikte richtingsverandering ondergaan komen ze via twee spleten S1 en S2 in ruimte II.
Deze ruimte wordt zo goed mogelijk vacuüm gehouden.
A
Leg met een schetsje uit waarom het nodig is minstens twee smalle spleten te
gebruiken wanneer we in ruimte II een smalle bundel elektronen willen krijgen.
In de figuur hiernaast is een deel van ruimte II nog
eens te zien. K en L zijn twee cirkelvormig gebogen
geleidende platen. Hiertussen bewegen elektronen
langs de stippellijn. De twee platen zijn aangesloten
op een regelbare spanningsbron.
B
Leg uit welke plaat de hoogste potentiaal
moet hebben.
De elektrische veldsterkte E tussen de platen K en L volgt
uit
de formule
V
E
d
waarin V (V) het potentiaalverschil tussen K en L is en d (m) de afstand. Elektronen met
een bepaalde kinetische energie Ekin cirkelen precies langs de stippellijn, andere
elektronen met een te hoge of een te lage energie maken een verkeerde baan. Ze
bereiken detector D dan niet omdat ze niet door spleet S3 gaan.
Voor de kinetische energie van de elektronen die detector D bereiken geldt de
formule
VeR
E kin 
2d
waarin R de straal die de elektronen doorlopen tussen K en L en e de elektronlading.
C
Leidt deze formule af uit bovenstaande gegevens.
In de opstelling is d = 2,0 (cm) en R= 10,0 (cm). De spanning V is ingesteld op 20,0 (V).
D
Bereken de kinetische energie van de elektronen die nu bij D arriveren in eV.
Alle elektronen die uit bron B komen hebben deze energie. In ruimte I kunnen ze 2 typen
botsingen met de kwikatomen ondergaan: ze kunnen elastisch botsen, waarbij ze hun
oorspronkelijke energie behouden, ze kunnen ook in-elastisch botsen waarbij ze een deel
van hun energie aan de kwikatomen afgeven. Door de spanning V tussen K en L te
varieren kunnen ook de elektronen die een deel van hun energie hebben verloren
geregistreerd worden. In de figuur hierboven is het aantal elektronen per sec dat D bereikt
(n/t) als functie van hun energie geregistreerd.
E
Leg uit waarom dit experiment Bohrs theorie van het atoom bevestigd.
F
Teken het energieschema van kwik dat uit dit experiment kan worden afgeleid.
G
Een kwiklamp geeft geel licht met ondermeer een golflengte van 579 nm. Bereken
de energie van de fotonen in eV.
H
Geef in het schema van vraag F aan welke overgang bij deze fotonen hoort.
H EEN KOPEREN RING
Een koperen ring is aan touwtjes aan een
hefboom opgehangen. Onder de ring bevindt zich een spoel met daarin een weekijzeren kern, die boven de spoel uitsteekt.
De spoel wordt op ‘n wisselspanningsbron
aangesloten. In de ring ontstaat daardoor
’n inductiestroom. De wisselstroom zorgt
er voor dat er een lorentzkracht die omhoog gericht is. Op enig moment is de situatie zoals getekend in de figuur hiernaast.
A
Leg uit dat de resultante van de Lorentzkrachten op de ring op dat moment
omhoog gericht is.
Met de hefboom wordt FL bepaald bij verschillende
hoogtes h van de ring boven de spoel. De hefboom is
homogeen en is voorzien van 21 pinnen op onderlinge
afstand 1,0 cm. Bij de meting die in de eerste figuur
getekend is hangen de ring (120 g), massa m1 (is ook
120 gr) en m2 (35 gr) aan de hefboom. Er is dan evenwicht. Hoogte h is op dat moment 1,0 cm.
B
Bereken de gemiddelde grootte van de Lorentzkracht FL die de ring dan ondervindt.
De meting wordt voor andere hoogtes h enkele malen
herhaald, op basis daarvan is de grafiek hiernaast gemaakt.
Vervolgens wordt de ring aan een veer opgehangen. De
wisselspanningsbron gaat uit. De spoel bevindt zich op
3,0 cm onder de ring. De ring gaat nu met een periode
van 1,26 s harmonisch trillen. De massa van de veer is
te verwaarlozen.
C
Bereken de veerconstante van de veer.
De ring ondervindt tijdens het trillen alleen zwaartekracht en de veerkracht. Als hoogte h boven de spoel
groter dan 3,0 cm is dan is de veerkracht kleiner dan
de zwaartekracht. De resultante van deze 2 krachten
is dan omlaag gericht en wordt hier Fneer genoemd. De
grootte van Fneer als functie van h voor h>3,0 cm is in
de figuur hiernaast weergeven, samen met de eerdere
grafiek van de lorentzkracht.
D
Bepaal uit Fneer nogmaals de veerconstante
De ring hangt weer stil op een hoogte van 3,0 cm en de
wisselspanningsbron wordt weer aangezet. De ring beweegt aanvankelijk omhoog.
E
Bepaal de versnelling van de ring als deze zich op
een hoogte van 4,0 cm boven de spoel bevindt.
F
Leg uit op welke hoogte boven de spoel de ring de
grootste snelheid behaalt.
G
Bereken deze met behulp van de grafiek hiernaast
van de kracht(en) tegen de hoogte.
I
MASSASPECTROMETER
Een massaspectrometer wordt gebruikt om vast te stellen welke waterstofisotopen er
bestaan. In de gaskamer wordt waterstofgas gedaan, door X-rays wordt het waterstof
geïoniseerd en versneld door de opening in de kathode. De eenwaardig positieve waterstofionen (1H) worden tot 5,0 x 106 m/s versneld door een onbekende spanning Vak.
A
Welke vergelijking geldt er voor het elektrisch versnellen van ionen van massa m tot
snelheid v.
B
Bereken het voltage Vak.
C
Bereken de snelheden v2 en v3 die de ionen van de isotopen 2H en 3H bij het verlaten
van het elektrisch veld hebben.
Na het elektrisch veld komen de 3 verschillende isotopen in een magnetisch veld B waar
ze gaan cirkelen en op massa gescheiden worden.
D
Teken de massa spectrometer en geef in je tekening aan hoe het B-veld gericht is.
E
Leg uit welke vergelijking er geldt voor het magnetisch rondcirkelen.
F
De straal van de 1H isotoop is 25 cm, bepaal de stralen van de 2H en 3H isotopen.