Lesgeheel 2: Spiegelen, verschuiven en draaien in het vlak

2
Spiegelen, verschuiven en
draaien in het vlak
Dit kun je al
1
2
3
4
de middelloodlijn van een lijnstuk herkennen en tekenen
een hoek meten en tekenen
de bissectrice van een hoek herkennen en tekenen
de coördinaat van een punt bepalen
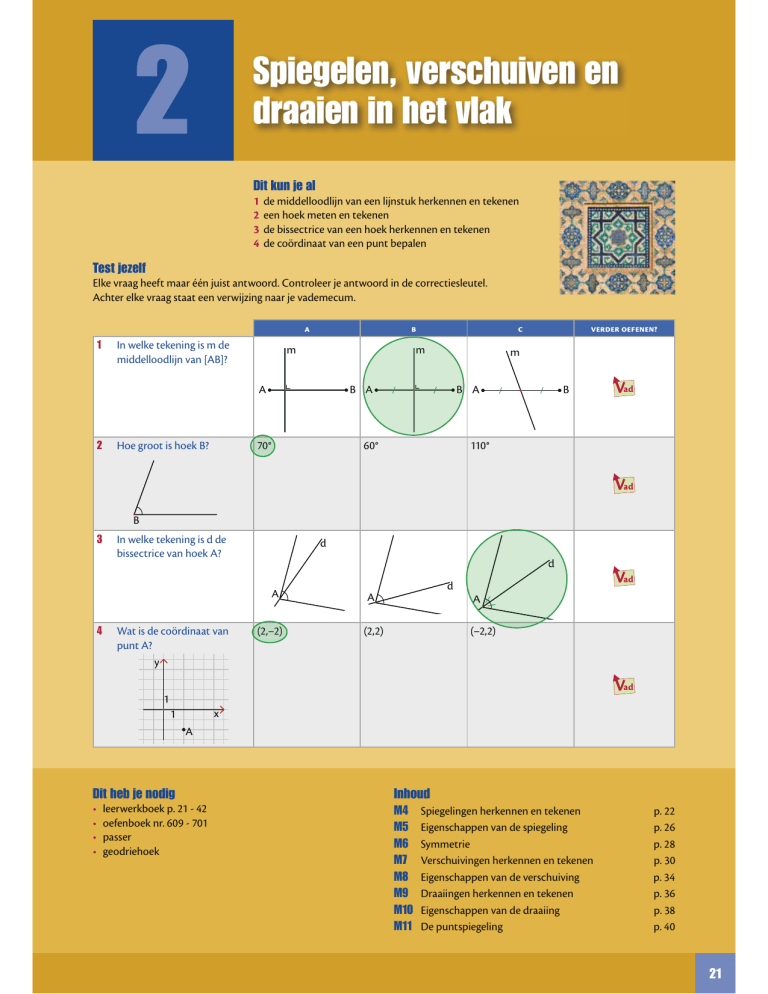
Test jezelf
Elke vraag heeft maar één juist antwoord. Controleer je antwoord in de correctiesleutel.
Achter elke vraag staat een verwijzing naar je vademecum.
A
1
In welke tekening is m de
middelloodlijn van [AB]?
B
m
m
A
2
Hoe groot is hoek B?
C
m
B A
70°
Verder oefenen?
B A
60°
B
ad
110°
ad
B
3
In welke tekening is d de
bissectrice van hoek A?
d
d
A
4
Wat is de coördinaat van
punt A?
y
(2,–2)
d
A
(2,2)
ad
A
(–2,2)
ad
1
x
1
A
Dit heb je nodig
Inhoud
•
•
•
•
M4
M5
M6
M7
M8
M9
M10
M11
leerwerkboek p. 21 - 42
oefenboek nr. 609 - 701
passer
geodriehoek
Spiegelingen herkennen en tekenen
Eigenschappen van de spiegeling
Symmetrie
Verschuivingen herkennen en tekenen
Eigenschappen van de verschuiving
Draaiingen herkennen en tekenen
Eigenschappen van de draaiing
De puntspiegeling
p. 22
p. 26
p. 28
p. 30
p. 34
p. 36
p. 38
p. 40
21
M4
Spiegelingen herkennen en tekenen
Op verkenning
a
Spiegelingen in de werkelijkheid
Dagelijks word je geconfronteerd met spiegels en
spiegelbeelden.
• Je staat voor de spiegel. Je zwaait met je rechterhand.
Wat doet je spiegelbeeld?
Mijn spiegelbeeld zwaait terug.
. . . ........................................................................ ....................................
•
Gebruikt je spiegelbeeld ook de rechterhand om te
zwaaien?
•
Je staat voor de spiegel. Je doet drie stappen achteruit. Wat doet je spiegelbeeld?
•
Raak met één vinger de spiegel aan. Wat doet je spiegelbeeld?
Neen, mijn spiegelbeeld zwaait met de linkerhand.
. . . ........................................................................ .................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
Mijn spiegelbeeld doet ook drie stappen achteruit.
. . . ........................................................................ .................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
Mijn spiegelbeeld raakt ook met één vinger de spiegel aan.
. . . ........................................................................ .................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
b
Het spiegelbeeld van een punt
• Teken het spiegelbeeld van het punt A. Noem dit punt A’.
•
Meet de afstand van A tot m en de afstand van A’ tot m.
Wat stel je vast?
d(A, m) = d(A', m)
. . . ........................................................................ ................................................
•
Teken het spiegelbeeld van het punt B. Noem dit punt B’.
•
Meet de afstand van B tot m en de afstand van B’ tot m.
Wat stel je vast?
d(B, m) = d(B', m)
A'
A
B'
B
. . . ........................................................................ ................................................
•
Wat is de onderlinge ligging van m en AA’ en BB’?
•
m " AA' en m " BB'
middelloodlijn
De rechte m is de .......................................
................................................
. . . ........................................................................ ................................................
m
van [AA’] en [BB’].
Wiskundetaal – begrippen
!
Het punt A’ is het spiegelbeeld van Beeld van een punt door een
het punt A door een spiegeling ten spiegeling:
sm(A) = A'
opzichte van (t.o.v.) spiegelas m
als en slechts als (a.s.a.)
AA' ! m
d(A,m) = d(A',m)
m de middelloodlijn is van [AA']
A
A’
m
Wiskundetaal – symbolen
wat gespiegeld wordt
(tussen ronde haakjes)
sm (A) = A'
spiegeling (kleine letter)
22
spiegelbeeld
naam van de spiegelas
(wordt een beetje lager geschreven)
Spiegelen, verschuiven en draaien in het vlak
Sa(A) = A'
lees je als het spiegelbeeld van A door
spiegeling t.o.v. spiegelas a is A'.
Stappenplan – het spiegelbeeld van een punt tekenen met de geodriehoek
$
"
#
$
%
&
'
(
(
"!
"(!
!
"
#!
"'!
!
"$&!
!
"#
'!
%! !
"%
$
$
""!
(!
"!!
*!
)!
*!
"!!
(!
""!
'!
"#
!
'
&
%
$
#
"
!
"
#
$
%
#
$
$
!
"$&!
"$&!
!
&
"
"
#
$! !
"&
#
#
'
(
"!
"(!
"
"
#!
"'!
#
$! !
"&
$
"%
%! !
"%
%! !
!
"#
'!
""!
(!
"!!
*!
)!
*!
"!!
(!
""!
(
'
%! !
"%
%
"&
$! !
"&
$! !
'!
"#
!
"$&!
!
&
%
$
#
"
!
"
#
$
%
&
"
"
#
#
"%
%! !
$
$
!
"$&!
!
"#
'!
""!
(!
"!!
*!
)!
*!
"!!
(!
""!
'
(
"!
"(!
&
"'!
#!
"'!
#!
#!
"'!
'
"(!
"!
"(!
"!
$! !
"&
A’
A
"&
$! !
%! !
"%
m
(
m
A
"'!
#!
'!
"#
!
"$&!
!
c
#
m
"(!
"!
!
!"Laat de loodlijn op de
tekenzijde samenvallen met de
spiegelas.
#"Verschuif de geodriehoek zodat
het punt A op de tekenzijde
A
ligt.
$"Meet de afstand van A tot aan
de spiegelas en duid op gelijke
afstand, aan de andere kant van
de spiegelas het punt A’ aan.
Het spiegelbeeld van een figuur
• Teken het spiegelbeeld van de figuur F ten opzichte van de spiegelas m. Hoe ga je te werk?
Teken het spiegelbeeld van alle hoekpunten. Verbind de hoekpunten.
. . . ........................................................................ .................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
F'
fig. F
m
•
Teken het spiegelbeeld van de cirkel t.o.v. spiegelas m. Hoe ga je te werk?
Teken s (O) = O' en dan een cirkel met middelpunt O en dezelfde straal als de
originele cirkel.
m
. . . ........................................................................
.................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
m
O
O’
Wiskundetaal – begrippen
Het spiegelbeeld van een figuur
vind je door de bepalende punten
van de figuur te spiegelen.
sm(ΔABC) = ΔA'B'C'
A
B
C
sm(ΔABC) = ΔA'B'C'
A’
B’
m
lees je als het spiegelbeeld van de
driehoek ABC t.o.v. de spiegelas m is de
driehoek A'B'C'.
C’
23
M4
Spiegelingen herkennen en tekenen (vervolg)
Oefeningen
WEER?
609
1
MEER?
610 - 612
c
m
B
A'
m
C'
A'
B'
e
A
D
m
B
A
d
C
2
b
A'
A
B'
C' = C
B
A
WEER?
613
614
a
Teken het spiegelbeeld t.o.v. de rechte m
a van de punten A, B en C
b van het lijnstuk AB
c van de driehoek ABC
d van het parallellogram ABCD
e van de cirkel C(C,r)
B'
B
C
D'
C'
C
m
A'
C'
m
B'
Teken de spiegelas x als je weet dat sx (A) = A'.
x
x'
x
A
x''
x'''
A = A’
A’
a
c
Hoeveel spiegelassen kun je tekenen?
Eén
Oneindig veel
.......................................................................... . . . . . . . . . . . . . . . . . . . . . . . . . .
b
x is de
middelloodlijn
............................................................ . . . . . . . van [AA'].
Hoeveel spiegelassen kun je tekenen?
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ....
b
is
Verklaar je antwoord. .Elke
. . . . . . . . . . . . .rechte
. . . . . . . . . . . . . . . . . . door
. . . . . . . . . . . . . . .A
. . . . . ....
een mogelijke spiegelas. Door één punt
kun je oneindig veel rechten tekenen.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ...
WEER?
615
3
Is figuur F' het beeld van figuur F door een spiegeling? Zo ja, teken dan de spiegelas.
a
b
c
fig. F’
fig. F’
fig. F
fig. F’
fig. F
fig. F
Ja
24
Spiegelen, verschuiven en draaien in het vlak
Ja
Neen
4
Kleur en vul aan.
a De rechte CF is de spiegelas. Kleur het spiegelbeeld van de blauwe
driehoek groen.
b Bekijk aandachtig het voorbeeld en vul in.
Voorbeeld: sBE ([CD]) = [AF]
B
A
[DC]
sAD([BC]) = .[FE]
...........
sCF([AB]) = .[ED]
...........
sBE([AF]) =
5
D
............
F
E
WEER?
617
Zijn de punten A en B t.o.v. dezelfde spiegelas gespiegeld? Zo ja, teken de spiegelas.
a
A
b
A’
A
c
B
A
a
B
B’
a
ja
A’
ja
d
e
B = B’
A’
ab
ja
B’
neen
f
B
A’
B
B’
A
A = A’
6
MEER?
616
C
A
A’
B
B’
B’
neen
neen
WEER?
618
Teken het spiegelbeeld van de rechte m t.o.v. de rechte a.
x'
a
x
y
m
y'
m'
m = m'
m
x'
a
x
m'
MEER?
619 - 621
y
x = x'
a
y'
a
2 punten . . .
Hoeveel punten moet je spiegelen om het spiegelbeeld van een rechte te kunnen tekenen? .....................................
b
Als de rechte de spiegelas snijdt:
–
–
c
Het snijpunt zelf
Hoeveel punten moet je nog extra spiegelen? . . .één
. . . . . . . . . . . punt
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
Wat is het spiegelbeeld van het snijpunt?
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
Wat merk je op als de rechte loodrecht op de spiegelas staat?
Het spiegelbeeld van de rechte valt samen met de oorspronkelijke rechte.
. . . ........................................................................ .................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ....
Wat moet je kunnen?
" spiegelbeelden herkennen
" het spiegelbeeld tekenen van een punt, lijnstuk,
rechte, vlakke figuren
" de spiegelas aanduiden of tekenen als een figuur en
zijn spiegelbeeld gegeven zijn
25
M5
Eigenschappen van de spiegeling
Op verkenning
Teken het spiegelbeeld van figuur ABCDE t.o.v. de rechte m. Het spiegelbeeld
van het punt A is het punt A’, het spiegelbeeld van B is B’, enz.
A
E
P
D
a
B'
B
A'
E'
P'
C
m
D'
C'
Lijnstukken
• Meet op de figuur de lengte van de lijnstukken.
1,5 cm
| B'C' | = . . .3
. . . . cm
.............................
| D'E' | = . . .1,7
. . . . . . . . cm
.........................
1,5 cm
| BC | = . . .3
. . . .cm
.............................
| DE | = . . .1,7
. . . . . . . . cm
.........................
| AB | = . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
| A'B' | = . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Wat stel je vast?
Het spiegelbeeld van de lijnstukken is even lang als de originele lijnstukken.
................................................................. .............................................................. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ......
•
Vergelijk in oefening 1b, 1c en 1d op p. 24 telkens |AB| en |A’B’|.
•
Wat kun je besluiten?
Elke spiegeling behoudt de lengte van een lijnstuk.
................................................................. .............................................................. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ......
b
Hoeken
• Meet op de figuur de grootte van de hoeken.
| A | = . . .135°
.................................
| B | = . . . 90°
.................................
| D | = . . 120°
..................................
| A' | = . . 135°
.................................
| B' | = . . .90°
................................
| D' | = . .120°
.................................
Wat stel je vast?
Het spiegelbeeld van de hoeken is even groot als de originele hoeken.
................................................................. .............................................................. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ......
•
Vergelijk in oefening 1c en 1d op p. 24 telkens | C | en | C' | .
•
Wat kun je besluiten?
Elke spiegeling behoudt de grootte van een hoek.
................................................................. .............................................................. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ......
c
De onderlinge ligging van rechten
• Wat is de onderlinge ligging van de rechten op de figuur? Vul in.
AB
•
//
.............
CD
A’B’
//
.............
C’D’
AB
.............
BC
A’B’
.............
B’C’
Wat kun je besluiten?
Elke spiegeling behoudt de onderlinge ligging van rechten.
................................................................. .............................................................. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ......
d
De oriëntatie van hoeken
• Teken op de figuur de rechte BP.
•
26
Teken het spiegelbeeld van de rechte BP. Moet je hiervoor het punt P spiegelen?
Spiegelen, verschuiven en draaien in het vlak
Neen
................................................
•
Verklaar je antwoord.
Een rechte wordt bepaald door twee punten. B en C zijn al gespiegeld.
. . . ........................................................................ .................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
•
B
Start bij punt A’ en wandel in wijzerzin door het spiegelbeeld. Welk hoekpunt kom je als eerste tegen? . .E’
. . . . . . . . . . . . .....
•
Wat stel je vast?
•
Start bij punt A en wandel in wijzerzin door de figuur. Welk hoekpunt kom je als eerste tegen?
. . . . . . . . . . . . . . . . ......
De oriëntatie van de hoeken is omgekeerd. De punten staan in omgekeerde volgorde.
. . . ........................................................................ .................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
Eigenschappen – de spiegeling
Het spiegelbeeld van een rechte is een rechte.
Het spiegelbeeld van een lijnstuk is een lijnstuk.
Het spiegelbeeld van een halfrechte is een halfrechte.
Elke spiegeling behoudt:
• de lengte van een lijnstuk;
• de grootte van een hoek;
(maar keert de oriëntatie van de hoeken om);
• de evenwijdigheid van rechten;
• de loodrechte stand van rechten.
A
A’
B B’
D
D’
C
De vorm en de grootte van een figuur blijft dus
behouden bij een spiegeling.
C’
m
Oefeningen
7
Gegeven: sm(A) = A' en | A | = 34°
a
b
WEER?
622 - 624
| A' | = . .34°
.............
MEER?
625
Welke eigenschap van de spiegeling heb je toegepast om dit antwoord te vinden?
Elke spiegeling behoudt de grootte van een hoek.
. . . ........................................................................ .................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
8
Teken door zo weinig mogelijk punten te spiegelen het spiegelbeeld …
a van een parallellogram.
1 Hoeveel punten moet je ten minste spiegelen
om een parallellogram te spiegelen?
B
A
A’
Twee
D’
................................................................. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .
2
Welke eigenschap(pen) heb je toegepast?
Elke spiegeling behoudt de hoekgrootte, de
lengte van een lijnstuk en
.................................................................
. . . . . . . . .de
. . . . . . . .evenwijdigheid.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .
B’
................................................................. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .
b
van een vierkant.
1 Hoeveel punten moet je ten minste spiegelen om een vierkant te
spiegelen?
Twee
................................................................. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .
2
A
D
Welke eigenschap(pen) heb je toegepast?
Elke spiegeling behoudt de grootte van een hoek,
de lengte van een lijnstuk
.................................................................
. . . . . . . . .en
. . . . . . . .de
. . . . . . . . evenwijdigheid.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .
D
C’
WEER?
626
MEER?
627 - 630
C
a
B
C
C’
B’
D’
A’
................................................................. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .
a
Wat moet je kunnen?
" de eigenschappen van de spiegeling onderzoeken in
oefeningen
" de eigenschappen van de spiegeling aantonen aan de
hand van een voorbeeld
" de eigenschappen van de spiegeling verwoorden
" de eigenschappen van de spiegeling toepassen om
het spiegelbeeld van een figuur te tekenen
27
M6
Symmetrie
Op verkenning
•
Teken een gelijkbenige driehoek met tophoek A die aan de volgende
voorwaarden voldoet.
| A | = 50°
| AB | = | AC | = 4 cm
•
Teken de bissectrice van de tophoek.
•
Spiegel het punt B t.o.v. de bissectrice en noem het B’.
•
Wat stel je vast?
B’ valt samen met C.
............................................................................................................................... . . . . . ....
A = A'
4 cm
Spiegel het punt C t.o.v. de bissectrice en noem het C’.
•
Wat stel je vast?
C’ valt samen met B.
............................................................................................................................... . . . . . ....
•
Spiegel het punt A t.o.v. de bissectrice en noem het A’.
•
Wat stel je vast?
A’ valt samen met A.
4 cm
B' = C
•
............................................................................................................................... . . . . . ....
•
Teken het spiegelbeeld van ∆ABC t.o.v. de bissectrice.
•
Wat stel je vast?
Het spiegelbeeld van de driehoek valt samen
met de originele driehoek.
B = C'
............................................................................................................................... . . . . . ....
Wiskundetaal – begrippen
a
a is symmetrieas van fig. F
!
Een symmetrieas van een figuur is
een rechte die de figuur op zichzelf
spiegelt.
Symmetrische figuren zijn
figuren met één of meerdere
symmetrieassen.
fig. F
Sa(fig. F) = fig. F
Oefeningen
WEER?
631 - 632
9
Zijn deze figuren symmetrisch? Indien ja, teken dan de symmetrieas(sen).
a
b
Neen
... ...........................................
28
c
Ja
.............. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Spiegelen, verschuiven en draaien in het vlak
d
Ja
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . .
Neen
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ............
10 Teken de andere helft van de vlinder.
WEER?
633
11 Teken de symmetrieas(sen).
WEER?
634
12 Teken in de symmetrische driehoeken alle symmetrieassen.
MEER?
635
a
Hoeveel symmetrieassen hebben ongelijkbenige driehoeken?
b
Hoeveel symmetrieassen hebben gelijkbenige driehoeken?
c
Hoeveel symmetrieassen hebben gelijkzijdige driehoeken?
A
B
E
0
.1
...................................................................................
.3
...................................................................................
....................................................................................
C
F
D
G
H
13 Teken de rest van de figuur als je weet dat x de symmetrieas is.
WEER?
636
x
Wat moet je kunnen?
" een symmetrieas herkennen in een figuur
" een symmetrieas van een figuur tekenen
" een figuur vervolledigen als de symmetrieas en een
deel van de figuur gegeven zijn
29
M7
Verschuivingen herkennen en tekenen
Op verkenning
a
Verschuivingen in de werkelijkheid
F
Tijdens een toneelstuk van ‘Finding Nemo’ moet
in het decor een school vissen worden verplaatst.
De vissen hangen allemaal aan elkaar vast en zijn
met een staafje aan het punt X vastgemaakt. Als
het punt X wordt verplaatst naar het punt Y, dan
verschuiven alle vissen in het decor. Zo gaat de
vis in punt A naar de plaats van de vis in punt A',
de vis in punt B gaat naar de plaats van de vis in
punt B', ... Naar welke plaats gaat de vis in punt
F? Noem het punt F' en teken de vis op de juiste
plaats.
b
X
A
C
E
B
D
F’
A’
Y
C’
E’
B’
D’
Het schuifbeeld van een punt
•
Teken in de bovenstaande figuur het lijnstuk AA’, het lijnstuk BB’, het lijnstuk CC’, het lijnstuk DD’ en
het lijnstuk FF’.
–
–
•
3,2 cm
|BB’|= . . .3,2
. . . . . . . . . .cm
........................
|CC’|= . .3,2
. . . . . . . . . .cm
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ......
3,2 cm
3,2 cm
|DD’|= ..................................
.............
|EE’| = . .3,2
. . . . . . . . . .cm
........................
|FF’|= ................................................
.....
De lijnstukken
Wat stel je vast? .............................
. . . . . . . . . . . . . .zijn
. . . . . . . . . . . allemaal
. . . . . . . . . . . . . . . . . . . . . . . . . . .even
. . . . . . . . . . . . . . .lang.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ......
Meet:
|AA’|=
.................................. . . . . . . . . . . . . .
Teken op [AA’] een pijl van A naar A’. Teken op [BB’] een pijl van B naar B’. Doe dit voor alle lijnstukken.
– Wijzen alle pijlen naar dezelfde kant? Of met andere woorden: hebben alle lijnstukken dezelfde zin?
Ja, alle lijnstukken hebben dezelfde zin.
................................................................. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
•
Wat is de onderlinge ligging van de rechte AA’, de rechte BB’, de rechte CC’, de rechte DD', ...
De rechten zijn evenwijdig.
•
Wat kun je nu vertellen over de richting van AA’, van BB’, ...
•
De dragers van de lijnstukken hebben dezelfde richting.
Meet: |XY| = 3,2
. . . . . . . . . .cm
. . . . . . . Vergelijk dit met de lengte van [AA’], van [BB’], van [CC’], ...
. . . ........................................................................ .................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
–
Weetje
. . . ........................................................................ .................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
Evenwijdige
rechten
hebben dezel
fde richting.
Wat stel je vast?
[XY] is even lang als de andere lijnstukken.
................................................................. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
•
Vergelijk de richting en de zin van [XY] met de richting en de zin van de andere lijnstukken.
– Wat stel je vast?
[XY] heeft dezelfde richting en zin als de andere lijnstukken.
................................................................. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
Alle lijnstukken met dezelfde lengte, richting en zin behoren tot dezelfde vector.
Wiskundetaal – begrippen
Een vector is een verzameling
lijnstukken die allemaal dezelfde
lengte, richting en zin hebben.
Een vector wordt voorgesteld
door een pijl.
#
XY$lees je als vector XY.
Y
P’
#
w$lees je als vector w.
X
P
# # #
XY$
, w$, PP'$stellen dezelfde
30
Spiegelen, verschuiven en draaien in het vlak
De pijl boven de letters geeft de zin
aan.
vector voor.
Wiskundetaal – begrippen
Een verschuiving wordt bepaald door
een vector.
Het punt A’ is het schuifbeeld van het
punt A door een verschuiving volgens
vector XY
Beeld van een punt door een
verschuiving:
a.s.a.
!
$(A) = A'
t#
XY
het lijnstuk AA’ evenwijdig is met het
lijnstuk XY
(de lijnstukken hebben dezelfde richting)
EN
het lijnstuk AA’ even lang is als het
lijnstuk XY
(de lijnstukken zijn even lang)
EN
de pijl van A naar A’ dezelfde zin heeft
als de pijl van X naar Y
(de lijnstukken hebben dezelfde zin).
[AA’] // [XY]
Y
X
A’
EN
| AA' | = | XY |
A
EN
[AA'] en [XY]
hebben dezelfde zin
Wiskundetaal – symbolen
$(A) = A'
t#
XY
wat verschoven wordt
(tussen ronde haakjes)
t#
$(A) = A'
XY
verschuiving (= translatie)
(kleine letter)
lees je als het schuifbeeld van
A door de verschuiving volgens
vector XY is A'.
schuifbeeld
de vector die de verschuiving bepaalt
(wordt een beetje lager geschreven)
Stappenplan – het schuifbeeld van een punt tekenen met de geodriehoek
A’
(
(
'
'
&
&
#
"
"
#
"
!
"!*!
#
"
"
!
#
"
#
#
$
"
%
#
"
(!"!
$
)!
*!
"!!
(!
""!
'!
"#!
&!
"$!
%!
"%!
$!
"&
!
"'#!
!
$
&
'
%
!
"!*!
(
$
"
#
"
(!"!
"!(!
"
$
%
$
!
"#
'! !
"#
'! !
$
)!
*!
"!!
(!
""!
'!
"#!
&!
"$!
%!
"%!
"!(!
"
$
"$!
&!
X
"%!
%!
"$!
&!
X
"&!
$!
Y
Y
"'!
#!
"%!
%!
A
%
A
"(!
"!
"&!
$!
$!
"&
!
"'#!
!
&
'
(
c
#
"'!
#!
Let op de zin van het lijnstuk.
Het punt A moet het beginpunt
zijn en het punt A' moet het
eindpunt zijn.
!
"(!
"!
!"Teken door het punt A een
evenwijdige met de rechte XY.
#"Plaats op de evenwijdige rechte
het punt A' zodat | XY | = | AA' |.
Het schuifbeeld van een figuur
•
#
#
Verschuif de figuur F volgens XY$
. Hoe ga je te werk? •
Verschuif de cirkel volgens AB$
. Hoe ga je te werk?
Teken
het schuifbeeld van elk hoekpunt.
. . . ........................................................................
........................
. . . . . . . . . . . . . . . . . . .m
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ....
Verbind
de schuifbeelden.
. . . ........................................................................
........................
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ....
Teken S (O) = O' en een cirkel met middelpunt
O' en dezelfde straal als de originele cirkel.
X
B
A Y
F
F’
O’
O
31
M7
Verschuivingen herkennen en tekenen (vervolg)
Wiskundetaal – begrippen
$(ΔABC) = ΔA'B'C'
t#
XY
Het schuifbeeld van een figuur vind
je door de bepalende punten van de
figuur te verschuiven.
t#
$(ΔABC) = ΔA'B'C'
XY
Y
X A’
A
lees je als het beeld van de driehoek
#
ABC door de verschuiving volgens XY$
(de vector XY) is de driehoek A’B’C’.
B’
B
C’
C
Oefeningen
WEER?
637 - 640
MEER?
641 - 644
14 Verschuif.
a
#
b
.
De verschuiving wordt bepaald door XY$
Verschuif de punten A, B, C en D.
A
#
De verschuiving wordt bepaald door TV$
.
Verschuif de punten E, F, G en H.
T X B
E
Y
C
D
A'
C'
WEER?
645
E'
F
G
B'
V
H
F'
G'
H'
D'
15 Werden de punten A en B door dezelfde verschuiving verschoven?
• Zo ja, verschuif het punt C volgens dezelfde verschuiving.
• Zo neen, verklaar waarom niet.
A’
a
B’
B’
A’
b
B’
A’
c
C'
A
B
A
C
d
A’
A
B
A’
e
B
C
f
C
A = A’
C
A
32
B’
B’
C
A
C
B = B’
B
Neen, de lijnstukken zijn niet even lang, ze behoren niet tot dezelfde vector.
a
. . . ........................................................................ .................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ....
b
. . . ........................................................................ .................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ....
c
. . . ........................................................................ .................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ....
d
. . . ........................................................................ .................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ....
e
. . . ........................................................................ .................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ....
f
. . . ........................................................................ .................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ....
Neen, de lijnstukken zijn niet evenwijdig, ze behoren niet tot dezelfde vector.
Ja
Neen, de lijnstukken hebben niet dezelfde zin, ze behoren niet tot dezelfde vector.
Neen, de lijnstukken zijn niet even lang, ze behoren niet tot dezelfde vector.
Ja
Spiegelen, verschuiven en draaien in het vlak
WEER?
646 - 649
16 Onderzoek de figuren. Is fig. F’ het beeld van fig. F door een verschuiving?
• Zo ja, teken de vector die deze verschuiving bepaalt.
• Zo neen, verklaar waarom niet.
a
c
b
e
d
fig. F
fig. F
fig. F
fig. F
fig. F
fig. F’
fig. F’
fig. F’
fig. F’
fig. F’
Ja
a
. . ........................................................................ ..................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
b
. . ........................................................................ ..................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
c
. . ........................................................................ ..................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
d
. . ........................................................................ ..................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
e
. . ........................................................................ ..................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
Neen, de lijnstukken zijn niet even lang, ze behoren niet tot dezelfde vector.
Ja
Ja
Neen, de lijnstukken zijn niet even lang, ze behoren niet tot dezelfde vector.
WEER?
650
651
17 Verschuif de figuren telkens volgens de gegeven vector.
a
b
t#u$(∆ABC) = ∆A'B'C'
A
t#v$(%ABCD) = %A'B'C'D'
B
v
C
u
B'
B'
A'
A
C'
D
c
A'
D'
B
C'
C
t#w$(%ABCD) = %A'B'C'D'
A
B
D
A'
C
B'
w
D'
C'
Wat moet je kunnen?
" het schuifbeeld van een punt, een lijnstuk, een rechte,
" het beeld van een verschuiving herkennen
" de vector die de verschuiving bepaalt aanduiden of tekenen een vlakke figuur tekenen
33
M8
Eigenschappen van de verschuiving
Op verkenning
#
Teken het schuifbeeld van figuur ABCDE. De verschuiving wordt bepaald door XY$
.
Het schuifbeeld van A is A’, het schuifbeeld van B is B’, enz.
Y
A'
X
A
B'
P'
B
E'
P
E
D
a
C'
D'
C
Lijnstukken
• Meet op de figuur de lengte van de lijnstukken.
1,2 cm
|AB| = ...................................................
|A’B’| = . .1,2
. . . . . . . . . cm
........................................
2,1 cm
|BC| = ...................................................
Wat stel je vast?
2,1 cm
|B’C’| = ...................................................
Het schuifbeeld van de lijnstukken is even lang als de originele lijnstukken.
. . . ........................................................................ .................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
•
Vergelijk in oefening 17 a, b en c op p. 33 |AB| en |A’B’|. Wat kun je besluiten?
Elke verschuiving behoudt de lengte van een lijnstuk.
. . . ........................................................................ .................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
b
Hoeken
• Meet op de figuur de grootte van de hoeken.
127°
| A' | = . .127°
...................................................
|A| =
.....................................................
| C | = . . 90°
......................................................
| C' | = 90°
......................................................
Wat stel je vast?
Het schuifbeeld van de hoeken is even groot als de originele hoeken.
. . . ........................................................................ .................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
•
Vergelijk in oefening 17 a, b en c op p. 33 | B | en | B' |. Wat kun je besluiten?
Elke verschuiving behoudt de grootte van een hoek.
. . . ........................................................................ .................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
c
De onderlinge ligging van rechten
• Wat is op de figuur de onderlinge ligging van de rechten? Vul in.
AB
•
//
...........
DC
A’B’
//
...........
D’C’
AB
...........
BC
A’B’
...........
B’C’
Vergelijk in oefening 17 de onderlinge ligging van de rechten in de figuren en hun schuifbeelden.
Wat kun je besluiten?
Elke verschuiving behoudt de onderlinge ligging van rechten.
. . . ........................................................................ .................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
. . . ........................................................................ .................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
•
Teken de rechte BP in het rooster.
•
Verschuif BP volgens t#
$.
XY
Moet je hiervoor het punt P verschuiven? . . Neen
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . ......
•
Verklaar je antwoord.
Het beeld van een rechte is een evenwijdige rechte.
. . . ........................................................................ .................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
•
Wat is de onderlinge ligging van BP en B’P’?
De rechte en haar beeld zijn evenwijdig.
. . . ........................................................................ .................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
34
Spiegelen, verschuiven en draaien in het vlak
Eigenschappen – de verschuiving
Het schuifbeeld van een rechte is een (evenwijdige) rechte.
Het schuifbeeld van een lijnstuk is een (evenwijdig) lijnstuk.
Het schuifbeeld van een halfrechte is een (evenwijdige) halfrechte.
A
X
Elke verschuiving behoudt:
• de lengte van een lijnstuk;
• de grootte van een hoek;
• de evenwijdigheid van rechten;
• de loodrechte stand van rechten.
Y
A’
B
B’
D
D’
C
C’
De vorm en de grootte van een figuur blijft dus behouden bij een verschuiving.
Oefeningen
18 Teken het beeld van het parallellogram ABCD volgens t#
$. Verschuif zo weinig mogelijk punten om je
XY
beeld te vinden.
a
b
X
Y
A'
Hoeveel punten moet je verschuiven? . .Eén
.......................
A
B'
Welke eigenschappen heb je toegepast?
verschuiving behoudt de lengte van
een
.De
. . ........................................................................
..........................
WEER?
652
B
D
D'
C'
C
De verschuiving behoudt de ..........................
evenwijdig.lijnstuk.
. . ........................................................................
van rechten. Een lijnstuk en zijn ..........................
beeld na
.heid
. . ........................................................................
verschuiving zijn evenwijdig. ..........................
.een
. . ........................................................................
#$.
19 Verschuif de rechte m volgens tAB
a Wat is de onderlinge ligging van een rechte en haar
schuifbeeld ?
b
A
B
X
rechte is evenwijdig met haar schuifbeeld.
.Een
. . ........................................................................
..........................
Hoeveel punten moet je ten minste verschuiven
Eén
om het beeld van een rechte te vinden? ......................
20
WEER?
653
X'
m
m'
#
Verschuif [XY] volgens vector w.$
M is het midden van [XY]. Is het beeld M’ van M ook
het midden van [X’Y’]? Verklaar.
X
Ja, de verschuiving behoudt de lengte
van een lijnstuk.
....................................................................................
..........................
M
X'
.................................................................................... . . . . . . . . . . . . . . . . . . . . . . . . . .
MEER?
655
Y
M'
Y'
21 Onderzoek.
a Kan vierkant B het beeld van vierkant A zijn door
WEER?
656 - 658
Ja, de zijden
een verschuiving? Verklaar. .....................
. . . . . .van
. . . . . . . .A
. . . .zijn
. . . . . . . .even
b
A
als de zijden van B en de hoeken zijn even groot.
.lang
. . ..................................................................................................
Kan fig. C het beeld van fig. A zijn door een
van A zijn
verschuiving? Verklaar. . Neen,
. . . . . . . . . . . . .de
. . . . . .zijden
. . . . . . . . ...........................
even lang als de zijden van C. ..........................
.niet
. . ........................................................................
MEER?
654
MEER?
659
660
C
B
Wat moet je kunnen?
" de eigenschappen van de verschuiving onderzoeken
in oefeningen
" de eigenschappen van de verschuiving verwoorden
" de eigenschappen van de verschuiving aantonen aan
de hand van een voorbeeld
" de eigenschappen van de verschuiving toepassen om
het schuifbeeld te tekenen
35
M9
Draaiingen herkennen en tekenen
Op verkenning
a
Draaiingen in de werkelijkheid
• Tom en Alec zitten in een reuzenrad. Nog 90° graden draaien en
hun bakje hangt helemaal bovenaan.
5
4
6
3
7
2
8
1
–
In welk bakje zitten ze als het rad met de klok meedraait (in wijzerzin)?
–
In welk bakje zitten ze als het rad niet met de klok meedraait (in tegenwijzerzin)?
–
–
Duid het punt (het centrum) aan waar het rad rond draait.
Vergelijk de afstand van de bakjes tot het centrum. Wat stel je vast?
In bakje 3
. .In
. . . . . . .bakje
. . . . . . . . . . . . . . . . .7
. . . . . . . . . . . . . . .....
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
De afstand tussen het centrum en de bakjes is telkens gelijk.
................................................................. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ....
•
•
Liesje zit in bakje 6 en het rad draait in tegenwijzerzin.
Hoe groot is de draaihoek die Liesje nog moet afleggen voor ze kan uitstappen?
225°
........................................ ....
De klasdeur draait open.
– Waarrond draait de klasdeur?
De scharnieren van de deur zijn het centrum van de draaiing.
................................................................. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ....
–
Welke draaizin heeft de deur van je klas als de deur open gaat?
Wijzerzin of tegenwijzerzin. (Afhankelijk van de deur.)
................................................................. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ....
b
Het draaibeeld van een punt
Als de auto 80 km/u rijdt, duidt de snelheidsmeter 80 aan.
B
•
Teken de naald voor 80 km/u.
•
. . . . cm
. . . . . . . . . en |AB| = .3
. . . . cm
.........
Meet |AC| = .3
•
Is de naald van lengte veranderd als ze 80 km/u aanduidt?
Neen
. . . ........................................................................ .................................................... . . . . .
•
Hoe groot is de hoek waarover de naald is gedraaid van 0 tot
80 km/u?
70°
A
C
. . . ........................................................................ .................................................... . . . . .
Wiskundetaal – begrippen
Het centrum van een draaiing is het punt waarrond
wordt gedraaid.
De draaihoek heeft een grootte (het aantal graden)
en een zin (wijzerzin of tegenwijzerzin).
Wijzerzin noteer je met een negatieve hoek.
Tegenwijzerzin noteer je met een positieve hoek.
36
Spiegelen, verschuiven en draaien in het vlak
Beeld van een punt
door een draaiing:
r(O,α)(A) = A'
!
Het punt A’ is het draaibeeld van het punt A door
een draaiing rond het punt O over een hoek α.
| AOA' | = α
| OA | = | OA' |
A’
O
70° (= tegenwijzerzin)
A
–70° (= wijzerzin)
A’’
wijzerzin: | AOA" | = –70°
tegenwijzerzin: | AOA' | = 70°
Weetje
alfabet
Griekse
t
t
e
h
it
u
k gebruik
letter
nde vaa .
u
k
α is een
is
w
e
t in d
uiden
en word ootten aan te d
r
g
k
e
o
om h
Wiskundetaal – symbolen
wat gedraaid wordt
(tussen ronde haakjes)
draaibeeld
r (O,α) (A) = A'
rotatie = draaiing
(kleine letter)
draaiingshoek
centrum van de draaiing
r (O,α) (A) = A'
lees je als het beeld van A door
draaiing met centrum O en over een
hoekgrootte α is A'.
Stappenplan – het draaibeeld van een punt tekenen met geodriehoek en passer
#
$ A’
&
A
A
'
A
(
"&!
$!
"'!
#!
"(!
"!
"%!
%!
"$!
&!
"#
'! !
%
""
(! !
#
$
)!
#
O
"
O
!
"!
*!
$
*!
"!!
"
(!
""!
!
$
O
'!
"#!
!"Teken een cirkel met centrum !
O en straal | OA |.
#"Teken [OA].
$"Teken hoek AOA' zodat A' op
de cirkel ligt. Let op de draaizin.
#
&!
"$!
"
"
#
%!
"%!
$
$!
"&
!
"'#!
!
%
"! !
"(
&
'
(
c
Het draaibeeld van een figuur
• Draai de figuur ABCDE rond centrum O over een
hoek van 120°.
• Hoe ga je te werk?
E’
Teken
het draaibeeld van alle
hoek. . . ........................................................................
..........................
punten.
Verbind de draaibeelden.
. . . ........................................................................
..........................
. . . ........................................................................ ..........................
D’
C
B
D
A
E A’
C’
B’
. . . ........................................................................ ..........................
O
Wiskundetaal – begrippen
r(O,–100°)(∆ABC) = ∆A'B'C'
Het draaibeeld van een figuur vind
je door de bepalende punten van de
figuur te draaien.
r(O,α)(∆ABC) = ∆A'B'C'
B’
A’
B
C
A
lees je als het draaibeeld van de
driehoek ABC rond centrum O over
hoek α is driehoek A'B'C'.
C’
–100° O
Oefeningen
WEER?
661
662
22 Bepaal de draaihoek.
23 Teken het draaibeeld van de punten A, B en C
door r(O,–40°).
-30°C F = F'
r(O,..........)
B
F
A
MEER?
666 - 679
A'C
F’
O
WEER?
663 - 665
B'
O
C'
Wat moet je kunnen?
" het draaibeeld van een punt, een lijnstuk, een rechte, een vlakke figuur tekenen
" een draaiing herkennen (het centrum van een draaiing vinden, de draaihoek van een draaiing bepalen)
37
M10
Eigenschappen van de draaiing
Op verkenning
Teken het draaibeeld van figuur ABCDE. De figuur wordt gedraaid
rond centrum O over een hoek van –100°. Het draaibeeld van A is A’,
het draaibeeld van B is B’, enz.
A
B
E
D
a
P
D’
C
C’
E’
A’
P’
B’
O
Lijnstukken
• Meet op de figuur de lengte van de lijnstukken.
1,2 cm
|AB| = ...................................................
|A’B’| = . .1,2
. . . . . . . . . cm
........................................
2 cm
|BC| = ...................................................
Wat stel je vast?
2 cm
|B’C’| = ...................................................
Het draaibeeld van de lijnstukken is even lang als de originele lijnstukken.
.................................................................. ............................................................. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
•
Vergelijk in oefening 22 de lengte van de overeenkomstige lijnstukken in de figuren en in hun draaibeeld.
•
Wat kun je besluiten?
Elke draaiing behoudt de lengte van een lijnstuk.
.................................................................. ............................................................. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
b
Hoeken
• Meet op de figuur de grootte van de hoeken.
|A| =
118°
..............
| A' | = . .118°
............
|B| =
90°
..............
| B' | = . . .90°
............
Wat stel je vast?
Het draaibeeld van de hoeken is even groot als de originele hoeken.
.................................................................. ............................................................. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
•
Vergelijk in oefening 22 de grootte van de hoeken in de figuren en in hun draaibeeld.
•
Wat kun je besluiten?
Elke draaiing behoudt de grootte van de hoek.
.................................................................. ............................................................. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
c
De onderlinge ligging van rechten
• Wat is op de figuur de onderlinge ligging van de rechten? Vul in.
AB
•
//
...........
DC
Wat stel je vast?
// D’C’
AB . . . . . . . . . . . BC
A’B’ . . . . . . . . . . . B’C’
Elke draaiing
. . . . . . . . . . . . . . . . . . . . . . . . . behoudt
. . . . . . . . . . . . . . . . . . . . . . . . . .de
. . . . . . . . onderlinge
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .ligging
. . . . . . . . . . . . . . . . . . . . .van
. . . . . . . . . . . .rechten.
.. . . . . . . . . . . . . . . . ....
A’B’
...........
Eigenschappen – de draaiing
Het draaibeeld van een rechte is een rechte.
Het draaibeeld van een lijnstuk is een lijnstuk.
Het draaibeeld van een halfrechte is een halfrechte.
B
Elke draaiing behoudt:
• de lengte van een lijnstuk;
• de grootte van een hoek;
• de evenwijdigheid van rechten;
• de loodrechte stand van rechten.
De vorm en de grootte van een figuur blijft dus behouden bij een draaiing.
38
Spiegelen, verschuiven en draaien in het vlak
C
B’
D
C’
A’
A
D’
O
Oefeningen
WEER?
680
681
24 Een cirkel met een oppervlakte van 20 cm² wordt gedraaid over een hoek van 180°.
20 cm²
a
Wat is de oppervlakte van het beeld van deze cirkel?
b
Welke eigenschap heb je gebruikt om je antwoord te vinden?
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ......
De draaiing behoudt de lengte van een lijnstuk; de straal blijft even groot.
. . . ........................................................................ .................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .....
WEER?
682
683
25 Gegeven: r(O, 90°)
Gevraagd: Kleur het draaibeeld van de blauwe driehoek.
O
WEER?
684
26 Teken door zo weinig mogelijk punten te draaien r(o,110°) (&ABCD) = &A'B'C'D'
a
Hoeveel punten heb je gedraaid om het beeld te vinden?
b
Welke eigenschap(pen) van de draaiing heb je gebruikt?
Twee
.............................................................................................. . . . .
MEER?
685 - 687
De draaiing behoudt de lengte van een lijnstuk, de hoekgrootte en de loodstand of de evenwijdigheid
van rechten.
.rechte
. . ........................................................................
....................................................
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ......
. . . ........................................................................ .................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ......
A B O
D C C’
B’
D’
A’
27 Het draaibeeld van de driehoek is fout. Aan welke
eigenschappen wordt niet voldaan?
De grootte van de draaihoek is verschillend. Hierdoor blijft de lengte
....................................................................................
. . . . . . . . . . . . .van
........
de lijnstukken en de grootte van
....................................................................................
. . . . . . . . de
.............
hoeken niet behouden, dus verandert
....................................................................................
.....................
de vorm en de grootte van de .driehoek.
....................................................................................
....................
WEER?
688
C
.................................................................................... . . . . . . . . . . . . . . . . . . . . .
C’
A
B
B’
O
Wat moet je kunnen?
" de eigenschappen van de draaiing onderzoeken in
oefeningen
" de eigenschappen van de draaiing aantonen aan de
hand van een voorbeeld
A’
" de eigenschappen van de draaiing verwoorden
" de eigenschappen van de draaiing toepassen om het
draaibeeld van een figuur te tekenen
39
M11
De puntspiegeling
Op verkenning
a
De puntspiegeling
Draai driehoek ABC over een hoek van 180° met K als centrum.
Het draaibeeld van het punt A is het punt A’, het draaibeeld van B
is B’ en het draaibeeld van C is C’.
• Meet de lengtes.
|AK| = . . .3,8
. . . . . . . . . .cm
............................
3,6 cm
1,7 cm
|CK| = .........................................
|BK| =
.........................................
|A’K| = . . . 3,8
. . . . . . . . . . cm
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . ......
3,6 cm
1,7 cm
|C’K| = ...........................................
.....
|B’K| =
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ......
Wat stel je vast?
K is het midden van de lijnstukken AA’, BB’ en CC’.
........................................................................................................................... . . ...
Deze bijzondere draaiing wordt ook een puntspiegeling genoemd.
C’
A’
B
K
A
B’
C
Wiskundetaal – begrippen
Een puntspiegeling is een draaiing met een
draaihoek van 180° of –180°.
r(O,180°)(F) = sO(F) = F'
Het centrum van de draaiing is het spiegelpunt.
O is het spiegelpunt.
A
B
C’
F
C
O
F’
B’
A’
Wiskundetaal – symbolen
wat gespiegeld wordt
(tussen ronde haakjes)
sO(A) = A'
spiegeling (kleine letter)
b
sO(A) = A'
spiegelbeeld
naam van het spiegelpunt
(wordt een beetje lager geschreven,
hoofdletter)
Het symmetriemiddelpunt
• Teken in vierkant ABCD de diagonalen.
• Noem het snijpunt van de diagonalen M.
• Spiegel ABCD t.o.v. het punt M.
• Wat merk je op?
lees je als het spiegelbeeld van
A door puntspiegeling met
spiegelpunt O is A'.
A = C'
B = D'
M
Het spiegelbeeld A’B’C’D’ valt
met ABCD.
.samen
. . ........................................................................
........................
. . . ........................................................................ ........................
D
40
Spiegelen, verschuiven en draaien in het vlak
= B'
C = A'
Wiskundetaal – begrippen
O is een symmetriemiddelpunt
van figuur F.
O
!
Een symmetriemiddelpunt van een
figuur is het spiegelpunt dat de figuur op
zichzelf spiegelt.
sO(fig. F) = fig. F
Oefeningen
28 Teken …
a sO(A), sO(B), sO(C)
b
C’
A
O
Y
A’
C
Y’
X
B’
O
B
het beeld van het lijnstuk sO([XY]).
WEER?
689
690
MEER?
691 - 693
X’
Wat is het punt O van figuur AC’B’A’CB?
Het punt O is het symmetriemiddelpunt van deze zeshoek.
. . . ........................................................................ ........................
c
sO(ruit ABCD)
A
C’
D
B
C
%c
O
B’
D’
&
29 Een kunstwerk van M.C. Escher.
A’
a Zoek het centrum van de draaiing die hond 1 op
hond 2 afbeeldt.
b
MEER?
694
........................................
Hoe groot is de draaihoek? . .180°
30 Onderzoek.
a Teken in de figuren de symmetriemiddelpunten in
blauw en de symmetrieassen in het rood. Let op!
Niet alle figuren zijn symmetrisch of hebben een
symmetriemiddelpunt.
b Hebben alle symmetrische figuren
Neen
een symmetriemiddelpunt?
....................
c Zijn alle figuren met een symmetrieNeen
middelpunt symmetrisch?
....................
31 Test je kennis van alle transformaties verder in het oefenboek.
Wat moet je kunnen?
" het beeld van een punt, een lijnstuk, een rechte, een vlakke figuur tekenen door een puntspiegeling
" het symmetriemiddelpunt van een figuur bepalen
MEER?
695
WEER?
696
697
MEER?
698 - 701
41
Problemsolving
1
De regelmatige vijfhoek OABCD (alle zijden zijn even lang en alle hoeken zijn
even groot) wordt gespiegeld t.o.v. de as OD, waarbij A wordt afgebeeld op A’.
De beeldvijfhoek wordt daarna gespiegeld t.o.v. OA’, waarbij D wordt afgebeeld
op D”. Zo ga je verder.
Na hoeveel keer spiegelen krijg je vijfhoek OABCD voor het eerst terug?
B
De som van de hoeken van een vijfhoek is. . .540°.
....................................................................................
. . . . . . . . . . .Eén
. . . . . . . . hoek
. . . . . . . . . . . .van
. . . . . . . ..een
. . . . . . . .regelmatige
.................................
A
vijfhoek bedraagt 540° : 5 = 108°. Eén keer spiegelen geeft hetzelfde resultaat als
....................................................................................
. . . . . . .met
. . . . . . . . .een
. . . . . . . . .draaiing
. . . . . . . . . . . . . . . . ..van
. . . . . . . . .216°,
. . . . . . . . . .…
......................
r(O,108°). Twee keer spiegelen komt overeen
Opdat de vijfhoek terug op de eerste plaats zou liggen moet de draaiingshoek een
veelvoud van 360° zijn. 2 · 360° = 720°. Dit is geen veelvoud van 108°.
3 · 360° = 1080° = 10 · 108°. De vijfhoek moet
....................................................................................
. . . . . . . .tien
. . . . . . . . .keer
. . . . . . . . . gespiegeld
. . . . . . . . . . . . . . . .. . . . . . . .worden.
..................................
.................................................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
Dylan moet een vierkant leggen met een aantal puzzelstukjes zoals hiernaast.
De puzzelstukjes mogen niet op elkaar liggen. Hoeveel puzzelstukjes heeft Dylan
nodig?
A 3
B 8
C 9
D 12
E 27
Als je een vierkant wilt bekomen moet het. . .aantal
....................................................................................
. . . . . . . . . . . . . . kleine
. . . . . . . . . . . . . .vierkantjes
. . . . . . . . . . .. . . . . . . . . . . .een
. . . . . . . . kwadraat
..........................
zijn. Omdat elk puzzelstukje uit drie vierkantjes bestaat, moet het totaal aantal
....................................................................................
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
vierkantjes deelbaar zijn door 3.
Kwadraten: 1
4
9
16
25
36
49
Kwadraten deelbaar door 3:
9
36
Met 9 vierkantjes (drie puzzelstukjes) kun .je
....................................................................................
. . . . geen
. . . . . . . . . . . .vierkant
. . . . . . . . . . . . . . . . . leggen.
. . . . . . . .. . . . . . . . .Met
. . . . . . . . .36
. . . . . .vierkantjes
......................
wel. Hiervoor heb je 36 : 3 = 12 puzzelstukjes nodig.
Maak de figuur symmetrisch door zo weinig mogelijk extra vierkantjes te kleuren.
.................................................................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
4
De cijfercombinatie van dit slot vind je als volgt.
• De eerste twee getallen zijn de coördinaatgetallen van punt Q. Q(30, 80)
• De twee volgende cijfers zijn de coördinaatgetallen van het spiegelbeeld van
Q (= Q’). Het punt Q wordt gespiegeld t.o.v. de rechte met als vergelijking x = 50.
• De twee laatste cijfers zijn de coördinaatgetallen van het snijpunt van [QQ’]
en de spiegelas.
De cijferslotcombinatie is: 30, 80, 70, 80, 50, 80
.................................................................................... ........................................... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
In een machine zitten twee tandwielen tegen elkaar. De straal van
het grote tandwiel is 3 keer zo groot als de straal van het kleine
tandwiel. Wat gebeurt er met het kleine tandwiel als het grote tandwiel één keer tegen de klok in rond draait?
Het kleine tandwiel draait in tegengestelde richting
.................................................................................... ........................................... . . . . . . . . . . . . . . . .
van het grote tandwiel.
.................................................................................... ........................................... . . . . . . . . . . . . . . . .
Omtrek kleine tandwiel: 2πr
.................................................................................... ........................................... . . . . . . . . . . . . . . . .
Omtrek grote tandwiel: 2π(3r) = 6πr
.................................................................................... ........................................... . . . . . . . . . . . . . . . .
Het kleine tandwiel draait drie keer met de klok mee.
42
Problemsolving
C
D
O
D''
A'