Practicum MMLogic

1
Practicum MMLogic
Inleiding
MMLogic is een computerprogramma waarmee digitale schakelingen kunnen worden gesimuleerd op
het scherm.
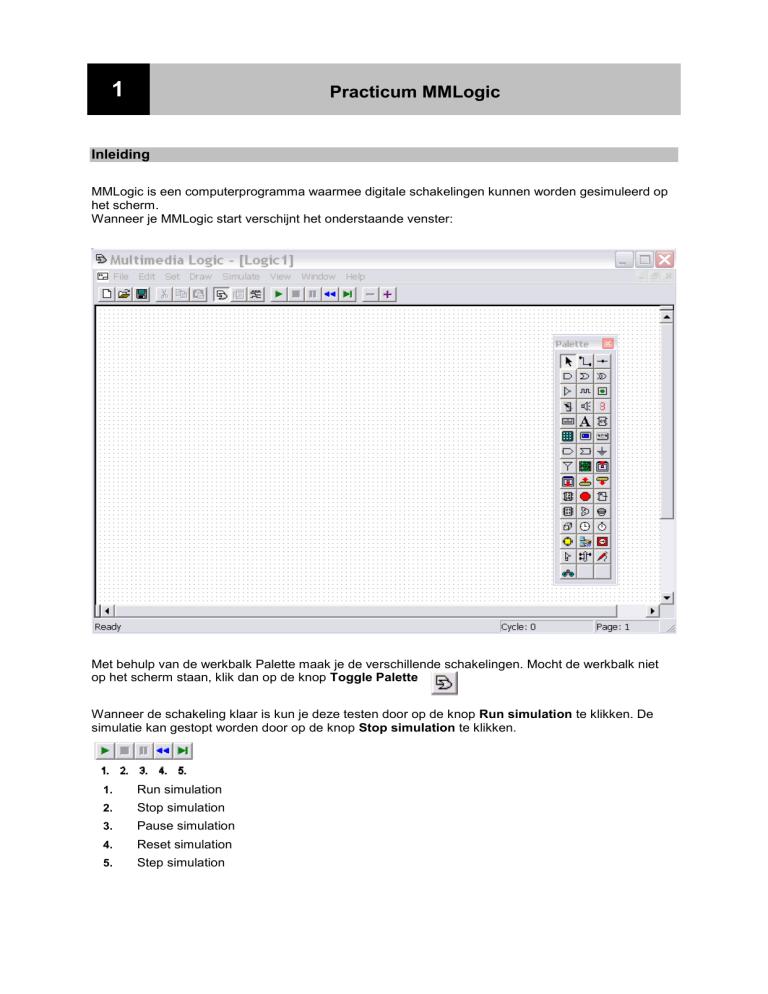
Wanneer je MMLogic start verschijnt het onderstaande venster:
Met behulp van de werkbalk Palette maak je de verschillende schakelingen. Mocht de werkbalk niet
op het scherm staan, klik dan op de knop Toggle Palette
Wanneer de schakeling klaar is kun je deze testen door op de knop Run simulation te klikken. De
simulatie kan gestopt worden door op de knop Stop simulation te klikken.
1.
Run simulation
2.
Stop simulation
3.
Pause simulation
4.
Reset simulation
5.
Step simulation
Turing ● Practicum MM-Logic
2
Logische operaties
De AND-poort
1. a. Maak de schakeling van de AND-poort.
Uit de werkblak Palette heb je de volgende componenten nodig:
Selector
Selecteren van een component
AND
AND-poort
Switch
Schakelaar of drukknop
LED
Light Emitting Diode (zuinig lampje)
Wire
Draad om twee componenten te verbinden
Text
Blokje om tekst toe te voegen aan het ontwerp
Door met de rechtermuisknop op een component te klikken
verschijnt een snelmenu. Met behulp van de keuze
Properties… kun je de eigenschappen van de component
wijzigen.
b. Test de schakeling, neem de waarheidstabel over in een Worddocument en vul kolom A and B in.
Zet vanaf nu alle andere antwoorden ook in dit Word-document!
A
B
A and B
0
0
..
0
1
..
1
0
..
1
1
..
Hoofdstuk 1 ● Informatieverwerkende systemen
3
De OR-poort
2. a. Maak de schakeling voor de OR-poort. Uit de werkblak Palette heb je de volgende extra
component nodig:
OR
OR-poort
b. Neem in je antwoorden, de volledig ingevude waarheidstabel over
van deze poort:
A
B
A or B
0
0
..
0
1
..
1
0
..
1
1
..
De NOT-poort
3. a. Maak de schakeling voor de NOT-poort. Uit de werkblak Palette heb je de volgende extra
component nodig: (inverter)
NOT
NOT-poort
b. Neem in je antwoorden, de waarheidstabel over van deze poort:
A
Not A
0
..
1
..
De XOR-poort
4. a. Maak de schakeling voor de XOR-poort. Uit de werkblak Palette heb je de volgende extra
component nodig:
XOR
XOR-poort
b. Neem in je antwoorden, de waarheidstabel over van deze poort:
A
B
A x-or B
0
0
..
0
1
..
1
0
..
1
1
..
4
Turing ● Practicum MM-Logic
5. a. Maak onderstaande schakeling. Test de schakeling.
b. Vul de waarheidstabel in en bewaar deze.
A
B
0
0
0
0
1
1
1
1
C
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
X
..
..
..
..
..
..
..
..
6. a. Beredeneer !!
In welke situaties zal de LED gaan branden. Maak zelf een waarheidstabel en vul hem vooraf
helemaal in.
b. Maak deze schakeling en controleer of je redenering klopte.
Hoofdstuk 1 ● Informatieverwerkende systemen
5
Chips
In de praktijk kom je geen losse poorten tegen, maar zijn ze geïntegreerd in een chip. Chips of IC’s
(geïntegreerde circuits) bestaan uit een stukje silicium waarop enkele poorten zijn aangebracht. Ze
worden gemonteerd in een plastic of keramische behuizing. Langs de rand bevinden zich rijen pinnen,
waarmee de chip wordt bevestigd op een printkaart.
In de afbeelding hieronder zie je een schematisch ontwerp van een chip met vier AND-poorten. Iedere
AND-poort heeft twee pinnen voor de input en een pin voor de output. Daarnaast heeft de chip een pin
voor de voeding (Vcc) en een pin voor de aarde (GND), die door alle poorten worden gebruikt. De
inkeping bij pin 1 zit er om de oriëntatie aan te geven.
Chips worden in vier klassen verdeeld op grond van het aantal poorten dat ze bevatten:
SSI-chips (Small Scale Integrated):
MSI-chips (Medium Scale Integrated):
LSI-chips (Large Scale Integrated):
VLSI-chips (Very Large Scale Integrated):
1 tot 10 poorten
10 tot 100 poorten
100 tot 100.000 poorten
meer dan 100.000 poorten
In het volgende deel van het practicum zul je het ontwerp van twee relatief eenvoudige chips bekijken:
de vergelijker en de opteller.
Turing ● Practicum MM-Logic
6
Vergelijker
De vergelijker, die hier getekend is, vergelijkt twee invoerwaarden A en B elk met een lengte van 4
bits. Wanneer beiden gelijk zijn zal de LED gaan branden (een 1) en anders niet (een 0).
De basispoort voor deze schakeling is de XOR, die een 0 als uitvoer geeft als de invoer gelijk is en
een als 1 als ze ongelijk zijn. Als twee waarden gelijk zijn, dan leveren alle vier de XOR-poorten een 0.
Deze vier signalen worden met OR-poorten gecombineerd. Als het resultaat van die combinatie 0 is
dan zijn de invoerwaarden gelijk, anders niet. Door als laatste poort een NOT te gebruiken wordt het
resultaat omgekeerd: is het resultaat een 1 (de LED brandt) dan zijn de waarden gelijk.
7.
a. Maak deze schakeling en controleer of zij correct werkt.
b. Aan de hand van dit ontwerp zou je een vergelijkerchip kunnen maken.
Hoeveel pinnen heeft deze chip nodig?
In de volgende schakeling worden de drie OR-poorten en de
NOT vervangen door een NOR-poort (NOT-OR-poort) met vier
ingangen. Een NOR-poort met vier ingangen maak je door de
Properties van een OR-poort te wijzigen (zie afbeelding
hiernaast).
Daarnaast worden de switches vervangen door twee keypads
en worden de waarden getoond op twee 7 segment LED’s.
Keypad
Hexadecimaal toetsenbord
7 segment LED
Display voor getallen
Hoofdstuk 1 ● Informatieverwerkende systemen
8.
7
a. Maak deze schakeling en controleer of zij correct werkt.
Denk eraan om de juiste uitgangen en ingangen met elkaar te verbinden.
b. Waaraan zie je het verschil tussen een OR-poort en een NOR-poort?
c.
Bouw een schakeling van een NOR-poort met 2 ingangen A en B. Vul de waarheidtabel van
deze NOR-poort. Bedenk hoe een NOR-poort met 4 inputs werkt.
d. Bouw een schakeling van een NAND-poort met 2 ingangen A en B.
Vul de waarheidstabel van de NAND-poort (NOT-AND) in.
Opteller
Een computer, die geen gehele getallen kan optellen, is ondenkbaar. Daarom vormt een schakeling
voor het uitvoeren van optellingen het hart van iedere CPU.
De half adder
Kijk eerst naar het optellen van 1-bits getallen:
0 + 0 = 00
0 + 1 = 01
1 + 0 = 01
1 + 1 = 10
Je zou het ook in een waarheidstabel kunnen zetten:
A
0
0
1
1
B
0
1
0
1
Tweetallen
0
0
0
1
Eenheden
0
1
1
0
Als je goed kijkt zie je dat onder de tweetallen het rijtje staan dat hetzelfde is als de output van een
and-poort geeft en onder de eenheden staat het rijtje van de xor poort. Daar kunnen we handig
gebruik van maken in onze 1-bits opteller:
Turing ● Practicum MM-Logic
8
9.
a. Maak de schakeling voor de half adder.
b. Test de schakeling, en controleer of de tabel klopt.
Deze schakeling wordt een half-adder (to add) genoemd. Met een half adder kun je alleen 1-bits
getallen bj elkaar optellen. Bij het optellen van grotere getallen krijg je een probleem van de
overdracht. Dit wordt hieronder uitgelegd.
De full adder
De half adder is geschikt om twee 1-bits getallen op te tellen en volstaat ook om de meest rechtse bit
van twee grotere getallen op te tellen. Voor het optellen van de andere bits heb je per positie een full
adder (volledige opteller) nodig, omdat er sprake is van overdracht van een bit (“1 onthouden”).
Voorbeeld:
Wanneer je de onderstaande optelling wilt doen gaat dat als volgt:
01
+ 11
100
Eerst tel je de eenheden op ( 0 opschrijven, 1 doorgeven naar tweetallen)
Dan tel je de tweetallen op ( 1+0+1 geeft 0 opschrijven en 1 doorgeven naar de viertallen.
Je krijgt dus een overdracht van de eentallen naar de tweetallen en van de tweetallen naar de
viertallen.
Met één half adder kun je eenheden bij elkaar optellen. Voor het optellen van de tweetallen moet je
eerst de tweetallen bij elkaar optellen en bij de uitkomst daarvan de overdracht. Dit kun je doen door
twee half adders achter elkaar te zetten:
10.
a. Maak de schakeling voor de full adder.
Hoofdstuk 1 ● Informatieverwerkende systemen
9
b. Test de schakeling en vul onderstaande waarheidstabel in, in je Word document:
A
(tweetallen)
0
0
0
0
1
1
1
1
B
(tweetallen)
0
0
1
1
0
0
1
1
Overdracht
eenheden
0
1
0
1
0
1
0
1
Som
..
..
..
..
..
..
..
..
Overdracht
tweetallen
..
..
..
..
..
..
..
..
De twee-bits opteller
We zullen als voorbeeld een twee-bits opteller bekijken. Voor het meest rechtse bit (de eenheden) heb
je een half adder nodig. Voor het tweede bit (de tweetallen) een full adder.
11
a. Maak de schakeling voor de twee-bits opteller.
b. Test de schakeling aan de hand van de volgende optellingen:
1+2 dus binair 0 1 + 1 0
2+2
1+3
3+2
3+3
Turing ● Practicum MM-Logic
10
De drie-bits opteller
Om twee drie-bits getallen op te tellen maak je een schakeling met een half adder voor het meest
rechtse bit (de eenheden) en twee full adders voor de overige twee bits (de tweetallen en de
viertallen).
12
a. Maak de schakeling voor de drie-bits opteller.
b. Test de schakeling aan de hand van de volgende optellingen:
2+3
3+3
1+6
4+2
6+5
7+7
Voor iedere bit dat de invoergetallen groter worden, moet er aan de schakeling een full adder worden
toegevoegd. Dit soort schakelingen wordt dan ook geïmplementeerd in een chip.
Tenslotte zullen we de switches vervangen door twee keypads en de invoerwaarden en de
uitvoerwaarde tonen op drie 7 segment LED’s.
Hoofdstuk 1 ● Informatieverwerkende systemen
13
a. Maak de nieuwe schakeling voor de drie-bits opteller.
b. Test de schakeling aan de hand van de volgende optellingen:
2+3
3+3
1+6
4+2
6+5
7+7
Lever je uitwerkingen op de afgesproken tijden in bij je docent.
11