Gegevens invoeren

Uitwerkingen opgaven hoofdstuk 6
6.1
Opgave 1
Ioniserende straling; eigenschappen en detectie
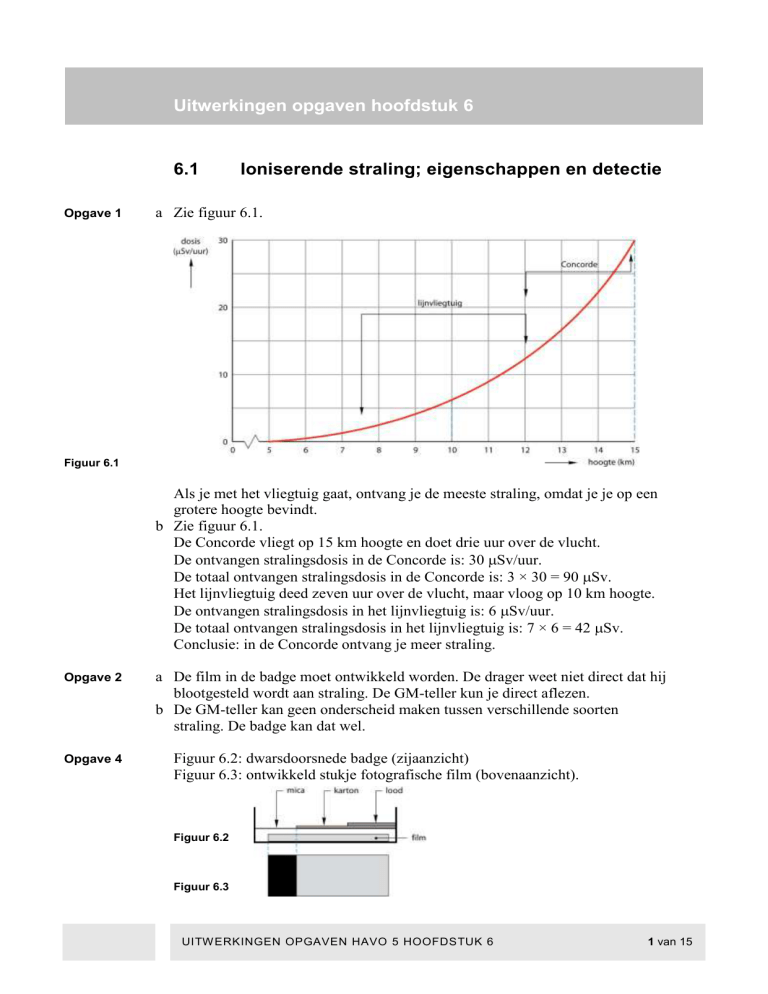
a Zie figuur 6.1.
Figuur 6.1
Als je met het vliegtuig gaat, ontvang je de meeste straling, omdat je je op een
grotere hoogte bevindt.
b Zie figuur 6.1.
De Concorde vliegt op 15 km hoogte en doet drie uur over de vlucht.
De ontvangen stralingsdosis in de Concorde is: 30 Sv/uur.
De totaal ontvangen stralingsdosis in de Concorde is: 3 × 30 = 90 Sv.
Het lijnvliegtuig deed zeven uur over de vlucht, maar vloog op 10 km hoogte.
De ontvangen stralingsdosis in het lijnvliegtuig is: 6 Sv/uur.
De totaal ontvangen stralingsdosis in het lijnvliegtuig is: 7 × 6 = 42 Sv.
Conclusie: in de Concorde ontvang je meer straling.
Opgave 2
Opgave 4
a De film in de badge moet ontwikkeld worden. De drager weet niet direct dat hij
blootgesteld wordt aan straling. De GM-teller kun je direct aflezen.
b De GM-teller kan geen onderscheid maken tussen verschillende soorten
straling. De badge kan dat wel.
Figuur 6.2: dwarsdoorsnede badge (zijaanzicht)
Figuur 6.3: ontwikkeld stukje fotografische film (bovenaanzicht).
Figuur 6.2
Figuur 6.3
UITW ERKINGEN OPGAVEN HAVO 5 HOOFDSTUK 6
1 van 15
a Het middengedeelte waar bèta- en gammastraling worden geregistreerd, en het
rechtergedeelte waar alleen gammastraling wordt geregistreerd, zijn even grijs.
Dit betekent dat er geen bètastraling aanwezig was.
b Het gedeelte voor gammastraling is lichtgrijs gekleurd. Het linkergedeelte, dat
gevoelig is voor alfa-, bèta- en gammastraling, is zwart. Dit betekent dat er
meer alfastraling dan gammastraling aanwezig was.
Opgave 4
Zie figuur 6.4.
Figuur 6.4
a De bron van de Rijn en de Waal ligt in de bergen in Zwitserland. Bij de
vorming van bergen komen relatief veel radioactieve mineralen aan de
oppervlakte. Deze stoffen worden door het water meegevoerd en, wanneer de
stroomsnelheid van het water afneemt, afgezet langs de oevers van de rivier.
De bron van de Maas bevindt zich op een hoogvlakte in Frankrijk. Dit is
geologisch gesproken een ouder gebied dan de Alpen. Op de hoogvlakte in
Frankrijk bevindt zich relatief minder radioactief materiaal aan de oppervlakte
dan in de Alpen.
b In Zuid-Limburg bevindt zich veel steenkool in de bodem. In dit erts komen
ook altijd veel radioactieve elementen, zoals radium, voor.
UITW ERKINGEN OPGAVEN HAVO 5 HOOFDSTUK 6
2 van 15
6.2
Radioactief verval
Opgave 5
a Het woord ‘model’ betekent in de genoemde context een vereenvoudigde
voorstelling van de werkelijkheid.
b Het woord ‘element’ betekent hier de verzameling van atomen met hetzelfde
aantal protonen in de kern.
Opgave 6
a Zie BINAS Tabel 25: 127 N; 137 N; 147 N; 157 N en
Z=7
b 147 N, voorkomen in de natuur 99,76%
A = 14, A = Z + N  N = 7
Opgave 7
a
b
c
d
Opgave 8
Een atoomkern bestaat uit 36 protonen en 50 neutronen
 Z = 36 en A = Z + N = 36 + 50 = 86. Zie BINAS Tabel 25: 86
36 Kr.
a Kr: zie BINAS Tabel 40A (gegevens van elementen) of Tabel 99 (periodiek
systeem der elementen): krypton.
82
84
86
b 4; zie BINAS Tabel 25: ( 80
36 Kr; 36 Kr; 36 Kr en 36 Kr); in de laatste kolom staat
een –.
85
–
Kr en 87
c 2; zie BINAS Tabel 25: ( 36
36 Kr); in de laatste kolom staat een  .
atoomsoort
3
2 He
87
36
Kr); in de laatste kolom staat een .
kerndeeltjes
2p + 1n
aantal elektronen
2
Z
2
A
3
He
2p + 2n
2
2
4
Ne
10 p + 12 n
10
10
22
Kr
36 p + 50 n
36
36
86
Ni
28 p + 40 n
28
28
68
U
92 p + 143 n
92
92
235
4
2
22
10
86
36
68
28
235
92
Opgave 10
N.
240
241
244
Zie BINAS Tabel 25: 239
94 Pu; 94 Pu; 94 Pu en 94 Pu.
Plutonium (Pu) heeft atoomnummer 94. De kern bevat dus 94 protonen. De
lading van de kern, uitgedrukt in elementaire ladingen, is +94e.
Een elementaire lading is gelijk aan 1,602 ∙ 10–19 C.
De lading van de plutoniumkern is dus 94 × 1,602 ∙ 10–19 = 1,506 ∙ 10–17 C.
Een atoom is per definitie neutraal, dus de lading bedraagt nul coulomb.
Nee, uit Tabel 25 van BINAS blijkt dat plutonium niet in de ‘vrije’ natuur
voorkomt.
81
85
Kr; 36
Kr en
d 3; zie BINAS Tabel 25: ( 36
Opgave 9
16
7
Neptunium: zie BINAS Tabel 40A (gegevens van elementen) of Tabel 99
(periodiek systeem der elementen): symbool Np.
a Np–237 ( 237
93 Np) zendt -straling (en -straling) uit.
–
Np–239 ( 239
93 Np) zendt  -straling (en -straling) uit.
UITW ERKINGEN OPGAVEN HAVO 5 HOOFDSTUK 6
3 van 15
b Neptunium–237:
237
233
4
93 Np  91 Pa  2 α  γ
of
237
233
4
93 Np  91 Pa  2 He  γ
Pa: zie BINAS Tabel 40A (gegevens van elementen) of Tabel 99 (periodiek
systeem der elementen): protactinium.
Neptunium–239:
239
239
0 
93 Np  94 Pu  1 β  γ
of
239
239
0
93 Np  94 Pu  1 e  γ
Pu: zie BINAS Tabel 40A (gegevens van elementen) of Tabel 99 (periodiek
systeem der elementen): plutonium.
Indium–114: zie BINAS Tabel 40A (gegevens van elementen) of Tabel 99
(periodiek systeem der elementen): symbool In
 indium–114: ( 114
49 In)
Opgave 11
a
114
49
In 
114
50
Sn  01β 
of
0
In  114
50 Sn  1 e
Sn: zie BINAS Tabel 40A (gegevens van elementen) of Tabel 99 (periodiek
systeem der elementen): tin.
114
0 
b 114
49 In  48 Sn  1 β
of
114
114
0
49 In  48 Sn  1 e
Cd: zie BINAS Tabel 40A (gegevens van elementen) of Tabel 99 (periodiek
systeem der elementen): cadmium.
114
49
Opgave 12
a 238 – 206 = 32
b Bij –-straling wordt in de kern een neutron omgezet in een proton en een
elektron. Daardoor verandert het massagetal niet. De verandering van het
massagetal is dan ook alleen te wijten aan het uitzenden van alfadeeltjes.
c Bij het uitzenden van een alfadeeltje neemt het massagetal met 4 af. Het
massagetal is met 32 afgenomen. Er zijn dan in de vervalreeks acht stappen
waarbij een alfadeeltje wordt uitgezonden.
6.3
Opgave 13
Halveringstijd en activiteit
Broom–82: zie BINAS Tabel 40A (gegevens van elementen) of Tabel 99
(periodiek systeem der elementen): symbool Br
 broom–82: ( 82
35 Br)
Nikkel–65: zie BINAS Tabel 40A (gegevens van elementen) of Tabel 99
(periodiek systeem der elementen): symbool Ni
 nikkel–65: ( 65
28 Ni)
a De activiteit is de hoeveelheid atomen die per seconde vervalt. De eenheid is
de becquerel (Bq) (zie ook BINAS Tabel 4: Bq = s–1).
UITW ERKINGEN OPGAVEN HAVO 5 HOOFDSTUK 6
4 van 15
65
b Broom–82 ( 82
35 Br) heeft een halveringstijd van 36 uur, nikkel–65 ( 28 Ni) heeft
een halveringstijd van 2,6 uur (zie BINAS Tabel 25). Broom heeft de grootste
halveringstijd.
c Broom–82 heeft de grootste halveringstijd. De kans dat een atoom broom–82
vervalt is dan kleiner. Broom–82 is stabieler dan nikkel–65.
d Het aantal atomen is in het begin vrijwel gelijk. Nikkel–65 heeft een kleinere
halveringstijd. Van nikkel–65 vervallen dan meer atomen per seconde dan van
broom–82. De activiteit van nikkel–65 is groter dan die van broom–82.
Opgave 14
Opmerking
De uitkomsten van de vragen van deze opgave zijn niet precies in
overeenstemming met elkaar omdat figuur 6.5 van het kernboek niet
nauwkeurig genoeg is getekend.
a Zie figuur 6.5.
In figuur 6.5 is te zien dat er van preparaat I na één uur meer atomen over zijn
dan van preparaat II. Er zijn dan minder atomen van preparaat I vervallen dan
van II. Preparaat I is daarom het stabielst.
b Het aantal kernen op t = 0 bedraagt N(0) = 5,0 ∙ 1014.
– na 1 halveringstijd (t½) zijn er nog 2,5 ∙ 1014 kernen;
– na 2 halveringstijden (2 ∙ t½) zijn er nog 1,25 ∙ 1014 kernen;
– na 3 halveringstijden (3 ∙ t½) zijn er nog 0,625 ∙ 1014 kernen.
Figuur 6.5
Figuur 6.5 (1): tI = 3 ∙ t½,I = 8,7 uur  de halveringstijd van preparaat I:
t½,I = 2,9 h
Figuur 6.5 (2): tII = 3 ∙ t½,II = 4,9 uur  de halveringstijd van preparaat II:
t½,II = 1,6 h
c Zie figuur 6.5.
De activiteit is het aantal kernen dat per seconde vervalt. In een (N,t)-diagram
is de activiteit op een bepaald tijdstip gelijk aan de steilheid van de raaklijn aan
de grafiek.
UITW ERKINGEN OPGAVEN HAVO 5 HOOFDSTUK 6
5 van 15
d
e
f
g
Opgave 15
Teken de raaklijn aan kromme I op t = 0 h en bepaal de steilheid ervan.
N 0
(0  5, 0  1014 )
 AI (0 h)  

 3, 2  1010 Bq
t0
4,35  3600
Zie figuur 6.5.
Teken de raaklijn aan kromme I op t = 2,8 h en bepaal de steilheid ervan
N 2,8
(0  4,1  1014 )
 AI (2,8 h)  

 1, 7  1010 Bq
t2,8
6,8  3600
Ja, de activiteit op t = 2,8 h is de helft van die op t = 0 h.
Zie figuur 6.5.
Het aantal atomen van preparaat II op t = 0 h: NII(0 h) = 5,0 ∙ 1014
Het aantal atomen van preparaat II op t = 5,0 h: NII(5,0 h) = 0,6 ∙ 1014
 het aantal atomen dat is vervallen
NII,vervallen = NII(0 h) – NII(5,0 h) = 4,4 ∙ 1014
Bij elke atoomkern van preparaat II die vervalt, wordt één alfadeeltje
uitgezonden. Preparaat II heeft dan ook 4,4 ∙ 1014 alfadeeltjes uitgezonden.
a Cesium–137: zie BINAS Tabel 40A (gegevens van elementen) of Tabel 99
(periodiek systeem der elementen): symbool Cs
 Cesium–137: ( 137
55 Cs)
Halveringstijd 137
55 Cs: 30 jaar (zie BINAS Tabel 25).
– na 1 halveringstijd (30 jaar) is er nog 50% over;
– na 2 halveringstijden (60 jaar) is er nog 25% over;
– na 3 halveringstijden (90 jaar) is er nog 12,5% over
 in het jaar 1986 + 90 = 2076 is er nog 12,5% over.
b Na 6,0 uur is er nog een kwart over, de oorspronkelijke hoeveelheid is dan
twee keer gehalveerd. Er zijn twee halveringstijden verstreken. De
halveringstijd bedraagt 3,0 uur.
Opgave 16
a Broom–82: zie BINAS Tabel 40A (gegevens van elementen) of Tabel 99
(periodiek systeem der elementen): symbool Br
 broom–82: ( 82
35 Br)
Halveringstijd 82
35 Br: 36 uur (zie BINAS Tabel 25).
87,5% van het aantal broomkernen is verdwenen  er is dan dus nog 12,5%
over.
– na 1 halveringstijd (36 uur) is er nog 50% over;
– na 2 halveringstijden (72 uur) is er nog 25% over;
– na 3 halveringstijden (108 uur) is er nog 12,5% over
 87,5% van de broomkernen is verdwenen na 108 uur  t = 1,1 ∙ 102 h
b Bij vraag a werd berekend dat er na 108 uur (drie halveringstijden) nog slechts
12,5% van de oorspronkelijke kernen overgebleven is.
Nog een halveringstijd later, dus na 108 h + 36 h = 144 h, resteert er dus
slechts 12 × 12,5% = 6,25% van de oorspronkelijke kernen.
Het aantal atomen dat nog over is na 144 h is 6,25% van 9,6 ∙ 1018 is:
6,0 ∙ 1017 = 0,6 ∙ 1018
Na 144 uur is dus vervallen: 9,6 ∙ 1018 – 0,6 ∙ 1018 = 9,0 ∙ 1018 kernen.
c De activiteit is rechtevenredig met het aantal atomen. Aangezien er van de
oorspronkelijke hoeveelheid atomen na 144 uur nog maar 6,25% over is, is er
UITW ERKINGEN OPGAVEN HAVO 5 HOOFDSTUK 6
6 van 15
ook nog maar 6,25% over van de oorspronkelijke activiteit. De activiteit na
144 uur is 6,25% van 7,4 ∙ 1014 Bq = 4,6 ∙ 1013 Bq.
Opgave 17
a Nee, de halveringstijd is een stofeigenschap en is niet afhankelijk van het
aantal atomen.
b Ja, de activiteit is rechtevenredig met het aantal atomen. In 2 gram zitten
tweemaal zoveel atomen. De activiteit is dan ook verdubbeld.
c Jood–131: zie BINAS Tabel 40A (gegevens van elementen) of Tabel 99
(periodiek systeem der elementen): symbool I
 Jood–131: ( 131
53 I)
Halveringstijd 131
53 I: 8,0 dag (zie BINAS Tabel 25).
Eerste manier
– na 1 halveringstijd (8,0 dag) is de activiteit
6,144  1015
Bq  3, 072  1015 Bq;
2
– na 2 halveringstijden (16 dagen) is de activiteit
3,072  1015
Bq  1,536  1015 Bq;
2
– na 3 halveringstijden (24 dagen) is de activiteit
1,536  1015
Bq  0, 768  1015 Bq;
2
– na 4 halveringstijden (32 dagen) is de activiteit
0,768  1015
Bq  0,384  1015 Bq;
2
– na 5 halveringstijden (40 dagen) is de activiteit
0,3840  1015
Bq  0,1920  1015 Bq  1,920  1014 Bq;
2
– na 6 halveringstijden (48 dagen) is de activiteit
1,920  1014
Bq  0,9600  1014 Bq  9, 600  1013 Bq;
2
– na 7 halveringstijden (56 dagen) is de activiteit
9,600  1013
Bq  4,800  1013 Bq;
2
– na 8 halveringstijden (64 dagen) is de activiteit
4,800  1013
Bq  2,400  1013 Bq;
2
– na 9 halveringstijden (72 dagen) is de activiteit
2,400  1013
Bq  1,200  1013 Bq;
2
– na 10 halveringstijden (80 dagen) is de activiteit
1,200  1013
Bq  0,6000  1013 Bq  6,000  1012 Bq;
2
 na 80 dagen is de activiteit van 6,144 ∙ 1015 Bq gedaald tot 6,000 ∙ 1012 Bq.
UITW ERKINGEN OPGAVEN HAVO 5 HOOFDSTUK 6
7 van 15
Tweede manier
Iedere halveringstijd daalt de activiteit met de helft:
6,144  1015
– na 1 halveringstijd is de activiteit
Bq;
2
6,144  1015
– na 2 halveringstijden is de activiteit
Bq;
22
6,144  1015
– na 3 halveringstijden is de activiteit
Bq;
23
enzovoort
6,144  1015
– na x halveringstijden is de activiteit
Bq;
2x
6,144  1015
6,144  1015
12
x

6,000

10

2

 1024  210
x
12
2
6,000  10
 na 10 halveringstijden (= 80 dagen) is de activiteit van 6,144 ∙ 1015 Bq
gedaald tot 6,000 ∙ 1012 Bq.
6.4
Effecten van ioniserende straling op mens en milieu
Opgave 18
a De gamma- en röntgenstraling worden sterk geabsorbeerd door het lood. Alfaen bètadeeltjes dringen helemaal niet door het lood heen.
b Bij nucleaire ongelukken kunnen ook radioactieve gassen en radioactief
besmette stofwolken vrijkomen. In het ziekenhuis komen deze gassen en
stofwolken niet voor.
Opgave 19
a D
Eontvangen
mweefsel
Eontvangen  Pstraling  t


Pstraling  5, 4  108 W  5, 4  108 J/s 

t  2,5 min  150 s

–8
 Eontvangen = 5,4 ∙ 10 × 150 = 8,10 ∙ 10–6 J
mpersoon  75 kg


mweefsel  0,020% van mpersoon 
0, 020
 mweefsel 
 75  15  103 kg
100
8,10  106
D
 5, 4  104 Gy
15  103




D  5, 4  104 Gy 
 H = 20 × 5,4 ∙ 10–4 = 1,1 ∙ 10–2 Sv
b H QD
Q -straling  20
UITW ERKINGEN OPGAVEN HAVO 5 HOOFDSTUK 6
8 van 15
Opgave 20
a Kalium–40: zie BINAS Tabel 40A (gegevens van elementen) of Tabel 99
(periodiek systeem der elementen): symbool K
 kalium–40: ( 40
19 K)
Kalium–40 is radioactief en vervalt onder uitzending van bètastraling:
40
40
0 
19 K  20 Ca  1 β
of
40
40
0
19 K  20 Ca  1 e
b De energie van één uitgezonden bètadeeltje bedraagt gemiddeld 0,44 MeV
 Eβ  0, 44 MeV  0,44  106  1, 602  1019  7, 05  1014 J
De activiteit van het radioactieve kalium in het spierstelsel bedraagt 3,1 ∙ 103 Bq
 per seconde: Estraling/seconde = 3,1 ∙ 103 × 7,05 ∙ 10–14 = 2,19 ∙ 10–10 J
 per jaar: Eontvangen = 2,19 ∙ 10–10 × 3,15 ∙ 107 = 6,90 ∙ 10–3 J
Eontvangen
6,90  103
D

 2,3  104 Gy
mspierweefsel
30
Opgave 21
a Radon–222: zie BINAS Tabel 40A (gegevens van elementen) of Tabel 99
(periodiek systeem der elementen): symbool Rn
 radon–222: ( 222
86 Rn)
Radon–222 is radioactief en vervalt onder uitzending van alfastraling (zie
BINAS Tabel 25):
222
218
4
86 Rn  84 Po  2 α
of
222
218
4
86 Rn  84 Po  2 He
b E = 5,486 MeV (zie BINAS Tabel 25)
E = 5,486 ∙ 106 × 1,602 ∙ 10–19 = 8,7886 ∙ 10–13 J
Het stralingsvermogen van het aanwezige radon–222 in de longen is:
P = 5,3 ∙ 10–14 W
 de stralingsenergie per seconde Estraling = 5,3 ∙ 10–14 J
5,3  1014
 Nα 
 6, 03  102
8, 7886  1013
c A2,5 dm3  6, 03  102 Bq
6,03  102
 24 Bq
2,5  103
d Per seconde: Estraling/seconde = 5,1 ∙ 10–14 J
 per jaar: Eontvangen = 5,3 ∙ 10–14 × 3,15 ∙ 107 = 1,67 ∙ 10–6 J
E

H  Q  D  Q  ontvangen 
mlongen 



Qα  20


mlongen  0,15 kg
1,67  106
 H  20 
 2,2  104 Sv
0,15
 A1 m3 
UITW ERKINGEN OPGAVEN HAVO 5 HOOFDSTUK 6
9 van 15
6.5
Opgave 22
Toepassingen van ioniserende straling in de
gezondheidszorg
Dit is bij alle situaties waarbij een stof wordt ingespoten om inwendige
bestraling toe te kunnen passen.
Opgave 23
a Een groot deel van de straling wordt niet geabsorbeerd door de tumor, maar
gaat door het lichaam heen.
b Alfastraling heeft een klein doordringend vermogen en kan niet door de wand
van de capsule heen dringen. Alfastraling bereikt in dit geval de tumor niet.
Daarom wordt er bètastraling gebruikt.
Opgave 24
a De stralingsdosis die de tumor ontvangt van drie bronnen is 1,5 keer de
stralingsdosis bij gebruik van één enkele bron. Een van de drie bronnen zendt
dan 0,5 keer de stralingsenergie uit van de oorspronkelijke hoeveelheid
energie. De intensiteit is dan ook de helft van de intensiteit bij gebruik van één
enkele bron.
b De tumor ontvangt een stralingsdosis die groter is dan bij het gebruik van één
enkele bron. Het omringende gezonde weefsel wordt echter bestraald door
maar een van de drie bronnen. Het gezonde weefsel ontvangt dan een kleinere
dosis, omdat er vanuit één bron minder straling komt.
c Bij een tumor die vlak onder de huid ligt heeft deze methode weinig zin, omdat
dan de straling sowieso door weinig gezond weefsel gaat. De methode zal dan
ook eerder bij diepliggende tumoren gebruikt worden.
6.6
Overige toepassingen van ioniserende straling
Opgave 25
a Nee, het bestraalde voedsel is niet radioactief geworden. Er komt geen straling
van af.
b Nee, het bestraalde voedsel is niet radioactief geworden. Je krijgt geen
radioactieve stoffen binnen.
c Ja, besmet voedsel is voedsel dat radioactieve stoffen bevat. Je ontvangt de
straling van deze stoffen.
d Ja, door besmet voedsel te eten, krijg je radioactieve stoffen binnen. Je bent
dan zelf ook besmet.
Opgave 26
a Zie figuur 6.6. d½ = 0,30 cm.
b Zie figuur 6.7 (1). Idoor = 44,5% van Iop.
Zie figuur 6.6 (2). Aflezen: dikte d = 0,33 cm.
c Er wordt minder straling doorgelaten dan het gemiddelde. Er wordt dus meer
geabsorbeerd. De staalplaat is dan bij P dikker dan het gemiddelde.
d Zie figuur 6.7 (3). Bij punt P: Idoor = 42% van Iop.
Zie figuur 6.6 (4). Aflezen: dikte d = 0,375 cm.
Eerste manier
0,373  0,33
 verschil in %:
 100%  13, 6%
0,33
 de afwijking in P is niet toegestaan.
UITW ERKINGEN OPGAVEN HAVO 5 HOOFDSTUK 6
10 van 15
Figuur 6.6
Figuur 6.7
Tweede manier
Voor de variatie in dikte is 10% toegestaan
 de dikte d van de plaat moet zijn: 0,33 ± 0,033 cm:
0,297 cm < d  0,363 cm
 de afwijking in P is niet toegestaan.
Opgave 27
a Het voedsel kan dan langer bewaard worden, zodat er grotere
voedselvoorraden aangelegd kunnen worden. Ook is er meer tijd om het
voedsel te verspreiden.
b De producenten van de isotopen hebben dan een nieuwe afzetmarkt voor hun
producten.
c Het produceren van meer isotopen levert meer radioactief afval op.
d Als de eigen oogst is mislukt, kan het land voedsel importeren of teren op
aangelegde voorraden.
e Enkele nadelen zijn:
– Het land moet veel geld steken in het bouwen van opslagplaatsen.
– Het opgeslagen of geïmporteerde voedsel heeft minder voedingswaarde.
– Er moet dan meer voedsel worden opgeslagen of geïmporteerd.
f Er wordt een eigen mening gevraagd, dus wordt hier geen antwoord gegeven.
6.7
Opgave 28
Kernenergie
a E  m  c 2 (BINAS Tabel 7) 

m  1  u  1, 66054  1027 kg 
c  2,99792458  108 m/s 

E = 1,66054 ∙ 10–27 × (2,99792458 ∙ 108)2
 E = 1,492419 ∙ 10–10 J
1,492419 1010
E
 931,49 106 eV  931,49 MeV
1,6021765 1019
UITW ERKINGEN OPGAVEN HAVO 5 HOOFDSTUK 6
11 van 15
b Molybdeen–99: zie BINAS Tabel 40A (gegevens van elementen) of Tabel 99
(periodiek systeem der elementen): symbool Mo
 molybdeen–99: ( 99
42 Mo)
Technetium–99m: symbool Tc  technetium–99m: ( 99m43Tc)
Mo 
99
42
Tc  01β 
99m
43
of
Mo  99m43Tc  01 e
Gebruik Tabel 25 en Tabel 7 uit BINAS en maak de volgende tabel.
99
42
99
42
99m
43
Mo
Tc
0 1
1
β
massa van het atoom (u)
98,90772
massa van de atoomkern (u)
98,88467964
98,90640
massa van het deeltje (u)
0,00054858
98,882881106
m = mvoor – mna = 98,88467964 – (98,882881106 + 0,00054858) = 0,00132 u
c Een massa van 1 u komt overeen met een energie van 931,49 MeV (zie BINAS
Tabel 7 of vraag a van deze opgave).
 0,00132 u komt overeen met een energie van 0,00132 × 931,49 = 1,23 MeV
d De berekende energie van het –-deeltje is gelijk aan de in BINAS Tabel 25
(laatste kolom) vermelde waarde. De energie die ontstaat bij het bètaverval
wordt meegegeven aan het elektron als kinetische energie. De kinetische
energie die de kern van technetium-99m krijgt is te verwaarlozen ten opzichte
van die van het elektron.
Opgave 29
a
235
92
90
?
U  01 n 
90
Sr  X  2 01 n
Sr: zie BINAS Tabel 40A (gegevens van elementen); Tabel 99 (periodiek
systeem der elementen) of Tabel 25 (Isotopen):
90
38
Sr.
144
1
U  01 n  90
38 Sr  54 X  2 0 n
X opzoeken: Tabel 99 (periodiek systeem der elementen) of Tabel 25
(Isotopen): 144
54 Xe
Xe = xenon (zie BINAS Tabel 40A (gegevens van elementen); Tabel 99
(periodiek systeem der elementen).
b Gebruik Tabel 25 en Tabel 7 uit BINAS en maak de volgende tabel.
235
92
235
92
90
38
144
54
U
Sr
1
0
n
massa van het atoom (u)
235,04393
massa van de atoomkern (u)
234,9934606
89,90775
89,88690396
Xe
143,93823
massa van het deeltje (u)
1,008665
m = mvoor – mna = 234,9934606 + 1,008665 – (89,88690396 + 143,93823 + 2
× 1,008665) = 0,159662 u
1 u = 1,66054 ∙ 10–27 kg (BINAS Tabel 7)
 m = 0,159662 × 1,66054 ∙ 10–27 = 2,651 ∙ 10–28 kg
UITW ERKINGEN OPGAVEN HAVO 5 HOOFDSTUK 6
12 van 15
c Eerste manier
E = m ∙ c2 = 2,651 ∙ 10–28 × (2,99792458 ∙ 108)2 = 2,383 ∙ 10–11 J
Tweede manier
m = 0,159662 u
Een massa van 1 u komt overeen met een energie van 931,49 MeV (zie BINAS
Tabel 7)
 0,159662 u komt overeen met een energie van 0,159662 × 931,49 =
148,7236 MeV = 148,7236 ∙ 106 × 1,6027165 ∙ 10–19 = 2,384 ∙ 10–11 J
Opgave 30
a
235
U-kern: zie BINAS Tabel 40A (gegevens van elementen) of Tabel 25
(isotopen): 235U-kern ( 235
92 U).
Twee middelgrote atoomkernen met de massagetallen 94 en 140:
middelgrote kern (1): ( 94?? X)
middelgrote kern (2): ( 140??Y)
U  01 n  94 X  140 Y  ?? 01 n
(totaal aantal protonen en neutronen)voor de kernreactie = 235 + 1 = 236
 (totaal aantal protonen en neutronen)na de kernreactie = 236
aantal protonen + neutronen 94X + 140Y = 94 + 140 = 234
 (totaal aantal vrije neutronen)na de kernreactie = 236 – 234 = 2
b Een van de middelgrote kernen: cesium (Cs).
Cesiumkern: zie BINAS Tabel 40A (gegevens van elementen) of Tabel 25
(isotopen): ( 140
55 Cs).
235
92
1
U  01 n  94Z X  140
55 Cs  2  0 n
ZX = 92 – 55 = 37
X opzoeken: Tabel 99 (periodiek systeem der elementen) of Tabel 25
(Isotopen): 94
37 Rb
(Dit isotoop van rubidium komt niet voor in Tabel 25 van BINAS.)
235
1
94
140
1
92 U  0 n  37 Rb  55 Cs  2  0 n
235
92
c Bij het uitzenden van een –-deeltje neemt het atoomnummer met één toe. Het
massagetal blijft gelijk  bij het uitzenden van drie –-deeltjes nemen de
opeenvolgende atoomnummers iedere keer met één toe en het massagetal blijft
gelijk. Bij de uiteindelijke kern die ontstaat, is dus het massagetal niet
veranderd en is het atoomnummer met drie toegenomen
Bij rubidium: 94
37 Rb (94 kerndeeltjes en 37 protonen)
De kern die ontstaan is, bezit dus nog steeds 94 kerndeeltjes, het aantal
protonen is 40 geworden  94
40 Zr (Zr = zirkonium, BINAS Tabel 99).
Bij cesium: 140
55 Cs (140 kerndeeltjes en 55 protonen).
De kern die ontstaan is, bezit dus nog steeds 140 kerndeeltjes, het aantal
protonen is 58 geworden  140
58 Ce (Ce = cerium).
UITW ERKINGEN OPGAVEN HAVO 5 HOOFDSTUK 6
13 van 15
Opgave 31
Californium-252: ( 252
98 Cf)
Tin-132: zie BINAS Tabel 40A (gegevens van elementen) ( 132
50 Sn).
Ook ontstaan er drie neutronen:
252
132
117
1
98 Cf  50 Sn  48 X  3  0 n
X opzoeken: Tabel 99 (periodiek systeem der elementen) of Tabel 25
(Isotopen): 117
48 Cd
252
98
Cf 
6.8
132
50
1
Sn  117
48 Cd  3  0 n
De kerncentrale
Opgave 32
a Nee, bij het produceren van de brandstofstaven ontstaat nog altijd CO2.
b Nee, ook het uranium raakt op korte termijn uitgeput.
c Het produceren van isotopen voor de gezondheidszorg, voor zover dat niet op
een andere manier gerealiseerd kan worden.
Opgave 33
a De resterende 75% wordt omgezet in warmte van het koelwater, het reactorvat
en de brandstofstaven.
b De centrale levert een elektrisch vermogen van P = 575 MW = 575 ∙ 106 W =
575 ∙ 106 J/s.
Dit is 25% van de door de splijtingsreacties geleverde energie.
De splijtingen leveren per seconde in de kerncentrale dus een energie op van
Ekern = 4 × 575 ∙ 106 = 2300 ∙ 106 J
Elke splijting levert een energie per seconde op van Esplijting = 175 MeV
Esplijting = 175 MeV = 175 ∙ 106 × 1,602 ∙ 10–19 = 2,804 ∙ 10–11 J
2300  106
 het aantal splijtingen per seconde is Nsplijting 
 8, 2  1019
11
2,804  10
c Eerste manier
Elke splijting levert een energie per seconde op van Esplijting = 175 MeV.
Een massa van 1 u komt overeen met een energie van 931,49 MeV (zie BINAS
Tabel 7)
 175 MeV komt overeen met een massaverschil van
175
mper splijting 
 0,18787 u 
931, 49
0,18787 × 1,66054 ∙ 10–27 = 3,1197 ∙ 10–28 kg
De totale massa-afname per uur mper uur = 8,2 ∙ 1019 × 3600 × 3,1197 ∙ 10–28 =
9,21 ∙ 10–5 kg
Tweede manier
De splijtingen leveren per seconde in de kerncentrale een energie op van
Ekern = 2300 ∙ 106 J
 de splijtingen leveren per uur een energie op van
Eper uur = 3600 × 2300 ∙ 106 = 8.2800 ∙ 1012 J
Dit komt overeen met een massaverandering per uur van
E
8, 2800  1012
m  2 
 9, 21  105 kg
8 2
c
(2,99792458  10 )
UITW ERKINGEN OPGAVEN HAVO 5 HOOFDSTUK 6
14 van 15
d Per uur neemt de hoeveelheid U-235 af met mper uur = 9,21 ∙ 10–5 kg
Dit is 0,080% van de totale hoeveelheid U–235 die per uur gebruikt wordt.
9, 21  105
In totaal wordt er dus mU- 235 
 100  0,115 kg verbruikt.
0,080
U–235 maakt slechts voor 4,0% deel uit van de totale hoeveelheid uranium
splijtstof.
0,115
Er is dus mverrijkt uranium 
 100  2,9 kg per uur nodig.
4, 0
e Als er hoog verrijkt uranium als brandstof wordt gebruikt, verandert de in
totaal omgezette massa niet. De massa van het uranium–235 verandert ook
niet. Omdat het uranium–235 een groter deel uitmaakt van het totale uranium,
neemt de massa van het uranium–238 af. De massa van het gebruikte uranium
wordt kleiner.
Opgave 34
De neutronen worden afgeremd, doordat ze bij botsingen kinetische energie
overdragen aan de kernen waarmee ze botsen. Er wordt meer energie
overgedragen als de massa van de kern gelijk is aan de massa van het neutron.
Aangezien een neutron een kleine massa heeft, zijn lichte kernen beter.
Opgave 35
a Het aantal elektronen van een kryptonatoom (36) is samen met het aantal
elektronen van een bariumatoom (56) even groot als het aantal elektronen van
een uraniumatoom (92). Dus de massa van de elektronen speelt geen rol bij de
berekening van het massadefect.
1
92
141
1
b 235
92 U  0 n  36 Kr  56 Ba  3 0 n
De massa voor de kernsplijting:
1
–25
mvoor = massa 235
+ 1,67493 ∙ 10–27 =
92 U + massa 0 n = 3,90299 ∙ 10
3,919739 ∙ 10–25 kg
De massa na de kernsplijting:
141
1
mna = massa 92
36 Kr + massa 56 Ba + 3 × massa 0 n =
1,52647 ∙ 10–25 + 2,33993 ∙ 10–25 + 3 × 1,67493 ∙ 10–27 = 3,916648 ∙ 10–25 kg
het massaverschil Δm = mvoor – mna = 3,919739 ∙ 10–25 – 3,916648 ∙ 10–25 =
3,091 ∙ 10–28 kg
E = m ∙ c2 = 3,091 ∙ 10–28 × (2,99792458 ∙ 108)2 = 2,778 ∙ 10–11 J
Massaverschil uitgedrukt in u × 931,49 = (3,091 ∙ 10–28/1,66 ∙ 10–27) × 931,49 =
173,4 MeV = 173,4 ∙ 106 × 1,6021765 ∙ 10–19 = 2,779 ∙ 10–11 J
c Bij een constant vermogen is het aantal splijtingen per seconde constant. Van
de drie vrijkomende neutronen veroorzaakt er gemiddeld één een nieuwe
splijting.
d Om het vermogen te vergroten, moeten er meer splijtingen per seconde
plaatsvinden. Dit kan door het aantal neutronen dat een nieuwe splijting
veroorzaakt te vergroten. Daarvoor moeten de regelstaven uit het uranium
geschoven worden tot het gewenste vermogen bereikt is. Om het vermogen
weer constant te krijgen, mag er weer slechts één neutron per reactie een
nieuwe splijting veroorzaken. Daarvoor moeten de regelstaven naar de oude
stand worden teruggeschoven.
e Als een reactor kritisch is, veroorzaakt gemiddeld één neutron per reactie een
nieuwe splijting. Het vermogen van de reactor is dan constant.
UITW ERKINGEN OPGAVEN HAVO 5 HOOFDSTUK 6
15 van 15