Opgave 1 Hoogspanningskabel (vwo – na1 – 2001 – tijdvak 1)

Opgave 1 Hoogspanningskabel (vwo – na1 – 2001 – tijdvak 1)
Tussen Rotterdam en Ommoord ligt een 3,0 km lange ondergrondse hoogspanningskabel.
De kabel heeft een weerstand van 7,2  10 2 . Hij bestaat uit een bundel koperdraden.
Elke draad heeft een cirkelvormige doorsnede met een diameter van 0,80 mm.
4p
4p
1
Bereken het aantal koperdraden in de kabel.
2
De hoogspanningskabel moet een elektrisch vermogen kunnen afleveren van maximaal 400 MW bij
een spanning van 150 kV.
Bereken het vermogen dat door warmteontwikkeling in de kabel verloren gaat als de gebruikers het
maximale elektrische vermogen afnemen.
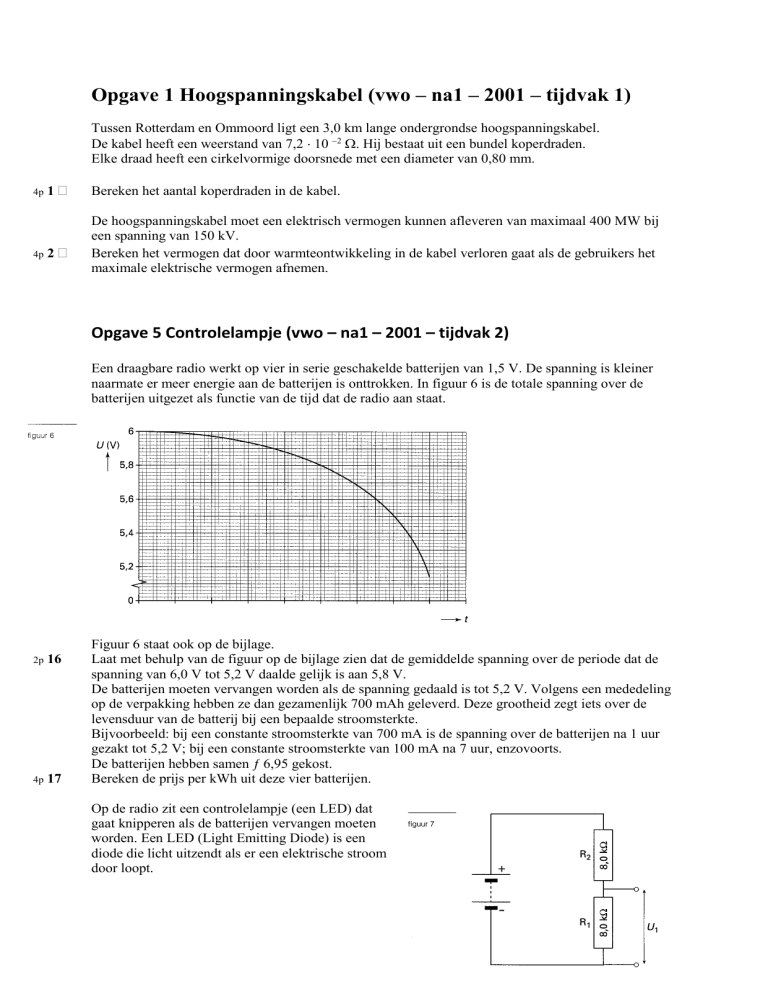
Opgave 5 Controlelampje (vwo – na1 – 2001 – tijdvak 2)
Een draagbare radio werkt op vier in serie geschakelde batterijen van 1,5 V. De spanning is kleiner
naarmate er meer energie aan de batterijen is onttrokken. In figuur 6 is de totale spanning over de
batterijen uitgezet als functie van de tijd dat de radio aan staat.
2p
16
4p
17
Figuur 6 staat ook op de bijlage.
Laat met behulp van de figuur op de bijlage zien dat de gemiddelde spanning over de periode dat de
spanning van 6,0 V tot 5,2 V daalde gelijk is aan 5,8 V.
De batterijen moeten vervangen worden als de spanning gedaald is tot 5,2 V. Volgens een mededeling
op de verpakking hebben ze dan gezamenlijk 700 mAh geleverd. Deze grootheid zegt iets over de
levensduur van de batterij bij een bepaalde stroomsterkte.
Bijvoorbeeld: bij een constante stroomsterkte van 700 mA is de spanning over de batterijen na 1 uur
gezakt tot 5,2 V; bij een constante stroomsterkte van 100 mA na 7 uur, enzovoorts.
De batterijen hebben samen ƒ 6,95 gekost.
Bereken de prijs per kWh uit deze vier batterijen.
Op de radio zit een controlelampje (een LED) dat
gaat knipperen als de batterijen vervangen moeten
worden. Een LED (Light Emitting Diode) is een
diode die licht uitzendt als er een elektrische stroom
door loopt.
Om de spanning te meten, is in de radio een spanningsdeler op de batterijen aangesloten. Zie figuur 7.
Deze spanningsdeler bestaat uit twee weerstanden R 1 en R 2 van ieder 8,0 k.
Ook als de radio uit staat, loopt er een stroom door de weerstanden. Daarom wordt aangeraden de
batterijen te verwijderen als de radio lange tijd niet gebruikt wordt.
Iemand vergeet dit en zet de radio met volle batterijen weg.
4p
18
Bereken hoe lang het duurt voordat de LED gaat knipperen.
Opgave 2 Temperatuursensor (vwo – na1 – 2002 – tijdvak 1)
Een temperatuursensor heeft drie aansluitingen. Aan elke aansluiting is een aansluitdraad met
een andere kleur bevestigd. Zie figuur 2.


5p
4
In de sensor bevinden zich een
temperatuurafhankelijke en een
temperatuuronafhankelijke weerstand.
Zie figuur 3.
Er wordt een meetplan opgesteld voor een
eenvoudig experiment. Het experiment moet
twee vragen beantwoorden:
Tussen welke twee aansluitdraden bevindt
zich de temperatuurafhankelijke weerstand?
Is de temperatuurafhankelijke weerstand een
NTC-weerstand?
Je hebt de beschikking over een batterij, een
stroommeter, een warmtebron en
aansluitdraden.
Beschrijf voor het meetplan:



• welke metingen je achtereenvolgens moet
doen;
• welke schakelingen je daarbij moet
gebruiken;
• hoe je op basis van de meetresultaten de
twee vragen kunt beantwoorden.
De waarden van de weerstanden van de
temperatuursensor worden nauwkeurig
gemeten. R1 heeft een waarde van 47,0 k.
Van R2 is de weerstand als functie van de
temperatuur weergegeven in figuur 4.
De rode draad wordt aangesloten op +5,0 V;
de zwarte wordt geaard.
De sensorspanning is de spanning tussen de
gele en de zwarte draad.
4p
5
Bepaal de sensorspanning bij een temperatuur
van 36 °C.
Opgave 5 Lantaarnpaal (vwo – na1 – 2002 – tijdvak 2)
Een lantaarnpaal op een tropisch eiland is voorzien van
een zonnepaneel en een lamp.
Zie figuur 6. Het zonnepaneel zet overdag zonlicht om in
elektrische energie en laadt daarmee een accu op.
's Nachts levert de accu een constante spanning van 24 V.
De lamp gebruikt dan een elektrisch vermogen van 36 W.
3p
17
Bereken de weerstand van de lamp.
Opgave l Elektromotor (vwo – na1 – 2003 – tijdvak 2)
De spanning over een kleine elektromotor
wordt geregeld met een spanningsbron van
12 V en een schuifweerstand.
Zie het schakelschema in figuur l.
Figuur 2 is een foto van de apparatuur.
-
figuur 2
De aansluitpunten voor de verbindingsdraden zijn in de figuur aangegeven met een wit
rondje. De foto staat vergroot op de bijlage.
4p
1
Teken in de foto de verbindingsdraden zodat de schakeling van figuur l ontstaat.
De schuifweerstand is 20,0 cm lang en is in te stellen van 0 Ω tot 40,0 Ω. Tijdens het hijsen
geldt: PS = 6,4 cm.
4p
3
Bereken de stroomsterkte die de spanningsbron levert.
Opgave 1 Valentijnshart (vwo – na1,2 – 2004 – tijdvak 1)
Met een Valentijnshart kun je een geheime geliefde
verrassen. Het hart bestaat uit een frame van metaaldraad
met tien lichtjes. Het hart kan worden vastgedrukt op een
batterij, die behalve als spanningsbron ook als voetstuk
dient. Figuur 1 is een foto van het Valentijnshart met zijn
schaduw.
De foto van figuur 2 toont de tien lichtjes van het
Valentijnshart. De lichtjes zijn LED’s.
Een LED is een halfgeleiderdiode die licht uitzendt als er
een elektrische stroom door loopt.
In figuur 3 is schematisch weergegeven hoe de LED’s zijn
geschakeld.
In de foto van figuur 2 zijn vier punten van het frame aangegeven met de letters A, B, C en D.
3p
3
Geef in figuur 3 op de uitwerkbijlage met de letters A, B, C en D aan welke punten overeenstemmen
met de punten A, B, C en D op de foto van figuur 2.
De LED in het midden van het hart is groter dan de andere negen. Deze negen LED’s zijn
identiek.
Met behulp van een spanningsmeter en een stroommeter kan het elektrisch vermogen worden
bepaald dat de grote LED opneemt wanneer hij licht uitzendt. Het frame van het
Valentijnshart kan worden losgekoppeld van de batterij. Zie de figuur op de uitwerkbijlage.
3p
4
Teken in de figuur op de uitwerkbijlage de verbindingsdraden die nodig zijn om het vermogen van de
grote LED te kunnen bepalen.
Uitwerkbijlage bij vraag 4:
De spanning over de grote LED is 5,0 V. De batterij levert een spanning van 9,0 V.
De spanning over de vijf LED’s aan de linkerkant noemen we UL.
De spanning over de vier LED’s aan de rechterkant noemen we UR.
Zie figuur 4.
4p
5
Leg aan de hand van figuur 4 uit dat UL kleiner is dan 2,0 V.
Opgave 5 Halogeenlamp (vwo – na1 – 2004 – tijdvak 2)
In figuur 5 zie je een 2,0 keer vergrote afbeelding van een buisvormige halogeenlamp.
Oscar en Loes doen een onderzoek aan deze halogeenlamp.
Ze beelden met een lens de gloeidraad van de brandende lamp sterk vergroot af op een
wand van het natuurkundelokaal. In figuur 6 zie je een deel van het beeld op de wand op ware grootte.
3p
17 
Uit het beeld op de wand kunnen ze zien dat de gloeidraad dubbelgewonden is.
De diameter van de gloeidraad is 40 µm. De gloeidraad is gemaakt van wolfraam.
Met behulp van een weerstandsmeter vinden zij dat bij kamertemperatuur de weerstand van de
gloeidraad 24  bedraagt.
Bereken de lengte van de gloeidraad.
Met behulp van een dimmer kunnen Loes en Oscar de spanning over de halogeenlamp langzaam
opvoeren van 0 tot 230 V. Bij verschillende waarden van de spanning willen zij de stroomsterkte door
de lamp meten. Zij maken daartoe eerst een voorspelling van de vorm van de (I,U)-karakteristiek.
Zij discussiëren over drie verschillende mogelijkheden: 1, 2 en 3. Zie figuur 7.
2p
18 
Leg uit welke van de mogelijkheden 1, 2 of 3 het beste overeenkomt met de te meten grafiek.
De halogeenlamp heeft bij 230 V een vermogen van 150 W.
Voor het meten van de stroomsterkte gebruiken Loes en Oscar een universeelmeter.
Figuur 8 is een foto van de “standenknop” van de gebruikte universeelmeter.
Het getal bij elke stand geeft het meetbereik aan.
In figuur 8 wijst de standenknop recht naar boven en is de meter uitgeschakeld.
3p
19 
Om de verschillende stroomsterktes die nodig zijn voor het verkrijgen van figuur 7 te bepalen, wordt
de standenknop in één vaste stand gebruikt.
Leg uit welke stand het best gebruikt kan worden om alle metingen uit te voeren.