Inductiestroom

Opgave 1
Een koperen draad is 60 cm lang.
Van de draad is rechthoekig raam gemaakt, dat 20 cm lang en 10 cm breed is.
10 cm
20 cm
Het draadraam wordt door Guus met een constante snelheid naar links getrokken een
homogeen magnetisch veld in. De sterkte van het veld is 0,36 T; de veldlijnen staan loodrecht
op het vlak van de tekening.
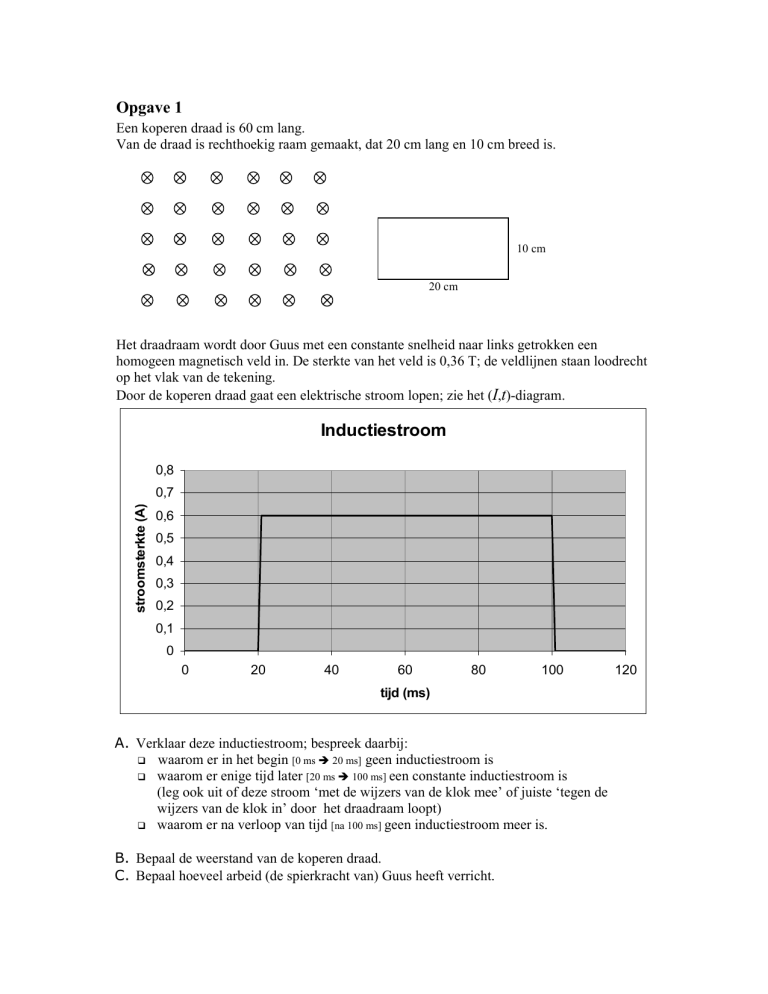
Door de koperen draad gaat een elektrische stroom lopen; zie het (I,t)-diagram.
Inductiestroom
0,8
stroomsterkte (A)
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
0
20
40
60
80
100
tijd (ms)
A. Verklaar deze inductiestroom; bespreek daarbij:
waarom er in het begin [0 ms 20 ms] geen inductiestroom is
waarom er enige tijd later [20 ms 100 ms] een constante inductiestroom is
(leg ook uit of deze stroom ‘met de wijzers van de klok mee’ of juiste ‘tegen de
wijzers van de klok in’ door het draadraam loopt)
waarom er na verloop van tijd [na 100 ms] geen inductiestroom meer is.
B. Bepaal de weerstand van de koperen draad.
C. Bepaal hoeveel arbeid (de spierkracht van) Guus heeft verricht.
120
Opgave 2
Een homogeen magnetisch veld heeft (opnieuw) een sterkte van 0,36 T.
B
A
Een tweewaardig ion vliegt met een snelheid van 4,0.10 2 m/s bij punt A het magnetisch veld
binnen; het ion verlaat het magnetisch veldbij punt B.
A. Leg uit of het ion positief of negatief geladen is.
B. Bereken de lorentzkracht op het ion.
C. Bewijs:
m=
B⋅q⋅r
.
v
D. Toon aan dat bovenstaande figuur niet ‘op ware grootte’ kan zijn.
Opgave 3
Een variac is een ideale transformator, waarbij men door middel van een schuifcontact S een
groter of een kleiner aantal secundaire windingen kan inschakelen.
Het aantal primaire windingen bedraagt 440.
De primaire spoel wordt aangesloten op een wisselspanning
Vp van 220 V, 50 Hz; de secundaire spanning Vs kan dan
worden gevarieerd van 6,0 V tot 260 V als het schuifcontact S
wordt verschoven.
A. Bereken tussen welke aantallen het aantal secundaire windingen kan worden gevarieerd.
B. Noteer:
de indeling van de
horizontale (tijd) as
de indeling van de verticale
(stroomsterkte) as.
Stroom PRIMAIRE spoel
stroomsterkte (A)
Men stelt de variac op 6,0 V in en
sluit op de secundaire spoel een
lampje (6,0 V; 0,50 A) aan.
In de grafiek staat de
stroomsterkte in de primaire
spoel als functie van de tijd.
Naam: ....................
30,00
20,00
10,00
tijd (s)
0,00
0
-10,00
-20,00
-30,00
0,01
0,02
0,03
0,04
0,05
Antwoorden
Opgave 1A
waarom er in het begin [0 ms 20 ms] geen inductiestroom is
Zolang het draadraam buiten het magneetveld is, ‘prikken’ er geen veldlijnen door het
omsloten oppervlakte binnen het draadraam (flux Φ = 0). De flux verandert dus niet
(fluxverandering ∆Φ = 0) en er wordt geen inductiespanning opwekt. Inductiestroom
is dus niet mogelijk.
waarom er enige tijd later [20 ms 100 ms] een constante inductiestroom is
Als het draadraam het magneetveld binnengaat, ‘prikken’ er steeds veldlijnen door het
omsloten oppervlak binnen het draadraam). De flux verandert en er wordt een
inductiespanning opwekt.
Omdat de grootte van het oppervlak binnen het magneetveld (door de constante
snelheid) lineair met de tijd toeneemt en omdat het magneetveld homogeen is, neemt de
omvatte flux lineair met de tijd toe (∆Φ / ∆t = constant). Er ontstaat een constante
inductiespanning en (omdat het draadraam van koper is) dus een constante
inductiestroom.
(leg ook uit of deze stroom ‘met de wijzers van de klok mee’ of juiste ‘tegen de wijzers
van de klok in’ door het draadraam loopt)
Deze inductiestroom is werkt de fluxverandering ‘tegen’.
De richting van deze stroom met de RHR:
De richting van de stroom is ‘tegen de wijzers van de klok in’; er wordt een magnetisch
veld opgewekt dat ‘het papier uit’ prikt, zodat de toename van de flux wordt bestreden.
De richting van deze stroom met de lorentzkracht en de LHR:
De richting van de stroom is ‘tegen de wijzers van de klok in’. Hierdoor loopt de stroom
in het linker-zijkant van het draadraam omlaag en werkt er een lorentzkracht naar
rechts, die de beweging van het draadraam hindert. Op de rechter-zijkant van het draadraam wertk geen
lorentzkracht, omdat dit deel van het draadraam zich nog niet in het magnetisch veld bevindt.
waarom er na verloop van tijd [na 100 ms] geen inductiestroom meer is.
Zodra het draadraam helemaal binnen het magneetveld is, ‘prikken’ er een constante
hoeveelheid veldlijnen door het omsloten oppervlakte binnen het draadraam (flux Φ =
constant). De flux verandert dus niet (fluxverandering ∆Φ = 0) en er wordt geen
inductiespanning opwekt. Inductiestroom is dus niet mogelijk.
Opgave 1B
∆Φ B ⋅ ∆A 0,36 ⋅ 0,020
=
=
= 0,090 V
∆t
∆t
80.10 −3
U 0,090
R= =
= 0,15 Ω
I
0,60
U ind =
Opgave 1C
Flor = B ⋅ I ⋅ l = 0,36 ⋅ 0,60 ⋅ 0,10 = 0,022 N
Fspier = Flor = 0,022 N
WF = F ⋅ s = 0,022 ⋅ 0,20 = 0,0043 J
Opnieuw opgave 1B (nu m.b.v. het antwoord van opgave 1C)
Q = P ⋅ ∆t = U ⋅ I ⋅ ∆t = I 2 ⋅ R ⋅ ∆t
Q
0,0043
→ R= 2
=
= 0,15 Ω
I ⋅ ∆t 0,60 2 ⋅ 0,080
Opgave 2A
LHR voor lorentzkracht
In punt A ondervindt het ion een lorentzkracht naar rechts.
Het magnetisch veld ‘prikt het papier in’.
Omdat het ion juist niet in de richting van de vingers van
een linkerhand beweegt, is hier sprake van een negatief ion.
B
A
Opgave 2B
Flor = B ⋅ q ⋅ v = 0,36 ⋅ 2 ⋅1,6.10 −19 ⋅ 4,0.10 2 = 4,6.10 −17 N
Opgave 2C
Fmpz = Flor
→
m ⋅v2
B⋅q⋅r
= B ⋅q ⋅v → m =
r
v
Opgave 2D
Stel het plaatje is wel ‘op ware grootte’: de straal van de cirkelbeweging ≈ 10 – 2 m.
De massa van het ion ≈ 10 – 24 kg (formule opgave 2C).
Er bestaan echter geen ionen met zo’n grote massa, omdat de massa van atomen (en dus van
ionen) ≈ 10 – 26 kg is. Conclusie: het plaatje is niet ‘op ware grootte’.
Opgave 3
Zie: http://www.natuurkunde.nl/artikelen/view.do?supportId=2143