Uitwerking SE Lineair programmeren

Uitwerking SE Lineair programmeren
Opgave 1
a.
b.
Deze bevat 1000 gr prot. , 1 gram vit. en 70 gram mineralen. Is dus genoeg
x kg soja en y kg graan
1. 100 x + 300 y ≥ 600  x + 3y ≥ 6
2. 0,4 x+ 0,2 y ≥1 
2x + y ≥ 5
3. 10 x + 20 y ≥ 52 
5x + 10 y ≥ 26
K = 40 x + 30 y ( of 0,3 x + 0,4 y)
2 pt
4 pt
y
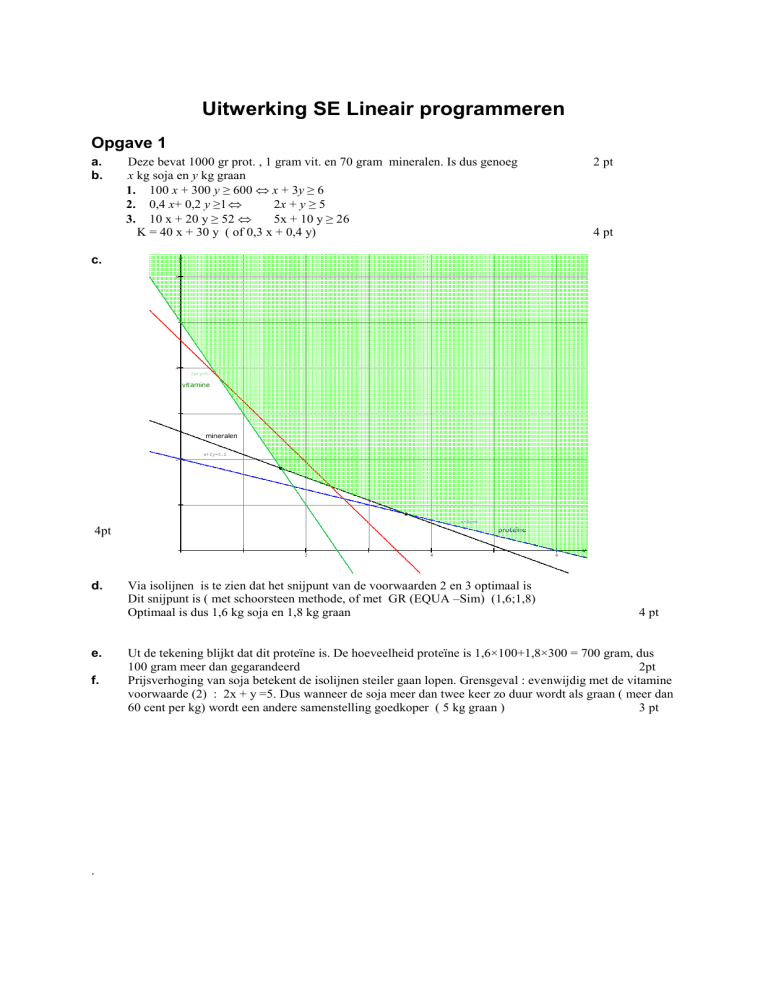
c.


2x+y=5
vitamine
mineralen

x+2y=5.2
x+3y=6
proteïne
4pt

d.
e.
f.
.

Via isolijnen is te zien dat het snijpunt van de voorwaarden 2 en 3 optimaal is
Dit snijpunt is ( met schoorsteen methode, of met GR (EQUA –Sim) (1,6;1,8)
Optimaal is dus 1,6 kg soja en 1,8 kg graan

x
4 pt
Ut de tekening blijkt dat dit proteïne is. De hoeveelheid proteïne is 1,6×100+1,8×300 = 700 gram, dus
100 gram meer dan gegarandeerd
2pt
Prijsverhoging van soja betekent de isolijnen steiler gaan lopen. Grensgeval : evenwijdig met de vitamine
voorwaarde (2) : 2x + y =5. Dus wanneer de soja meer dan twee keer zo duur wordt als graan ( meer dan
60 cent per kg) wordt een andere samenstelling goedkoper ( 5 kg graan )
3 pt
opgave2
a)
voorwaarden: [ 6 pt]
0. b+g ≤ 400 [niet vergeten !]
1. w ≤ 200  b+g ≥200
2. b≥ g
3. 100 b + 50 w ≤ 25 000 
100 b + 50(400−b−g) ≤ 25 000 
50 b −50 g + 20 0000 ≤ 25 000 
50 b −50 g ≤ 5 000 
b − g ≤ 100
4. 15 b + 6 g ≤ 3000  5b + 2g ≤ 1000
b)
[6 pt]
c)
[2 pt]
O = 1500 b + 1000 g + 500 ( 400−b−g) = 200 000 + 1000 b + 500 g
d)
[4 pt]
Een iso-opbrengst lijn is (bijv) 2b + g =400.
Deze gaat door (200;0) en (0;400)
De richting van deze lijn(en) geeft aan dat het beste punt is het snijpunt van [2]en [ 4] dus
Ca 142,9 ha bos; 142,9 ha grasland, en de rest (ruim 114 ha) water
( De opbrengst hiervan bedraagt € 414.285,71 )
e)
De opbrengst per ha bos noemen we p [4 pt]
grensgeval is als de isolijnen evenwijdig lopen aan de lijn die hoort bij voorwaarde 4
Dus
p-500
500
5
2
Moet een verhoudingstabel zijn
Hieruit volgt : p−500 = 1250  p =1750
Dus bij een opbrengst van meer dan 1750 euro per ha brengt een andere verdeling meer op ( Punt C
wordt dan optimaal)
Er is nog een grensgeval ( maar doorvoor is een grote opbrengstdaling nodig)
De isolijn kan ook nog evenwijdig lopen aan AD
p-500
500
1
-1
Hieruit volgt p =0
Bij een opbrengst van minder dan 0 euro per ha bos, is punt A optimaal
Maar dat is wel heel vreemd…..