Sleetje op helling, inclusief uitwerking

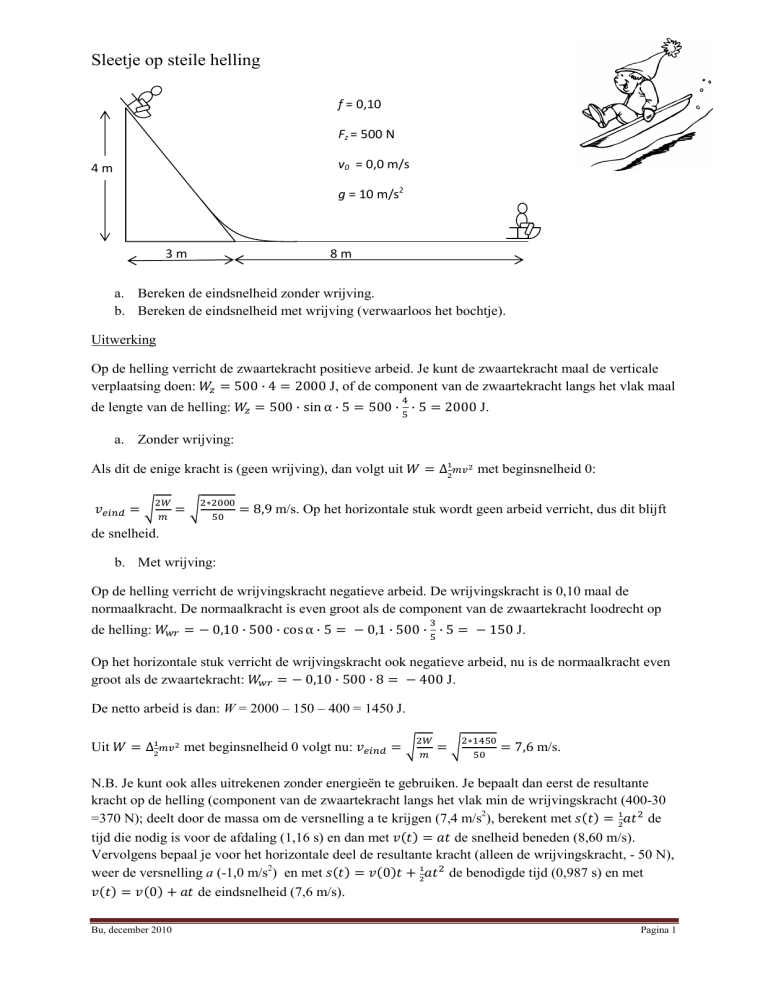
Sleetje op steile helling
f = 0,10
Fz = 500 N
v0 = 0,0 m/s
4m
g = 10 m/s2
3m
8m
a. Bereken de eindsnelheid zonder wrijving.
b. Bereken de eindsnelheid met wrijving (verwaarloos het bochtje).
Uitwerking
Op de helling verricht de zwaartekracht positieve arbeid. Je kunt de zwaartekracht maal de verticale
verplaatsing doen: ܹ௭ = 500 ∙ 4 = 2000 J, of de component van de zwaartekracht langs het vlak maal
ସ
de lengte van de helling: ܹ௭ = 500 ∙ sin α ∙ 5 = 500 ∙ ହ ∙ 5 = 2000 J.
a. Zonder wrijving:
Als dit de enige kracht is (geen wrijving), dan volgt uit ܹ = ∆భమ௠௩ మ met beginsnelheid 0:
ଶௐ
‫ݒ‬௘௜௡ௗ = ට ௠ = ට
ଶ∗ଶ଴଴଴
ହ଴
= 8,9 m/s. Op het horizontale stuk wordt geen arbeid verricht, dus dit blijft
de snelheid.
b. Met wrijving:
Op de helling verricht de wrijvingskracht negatieve arbeid. De wrijvingskracht is 0,10 maal de
normaalkracht. De normaalkracht is even groot als de component van de zwaartekracht loodrecht op
ଷ
de helling: ܹ௪௥ = − 0,10 ∙ 500 ∙ cos α ∙ 5 = − 0,1 ∙ 500 ∙ ହ ∙ 5 = − 150 J.
Op het horizontale stuk verricht de wrijvingskracht ook negatieve arbeid, nu is de normaalkracht even
groot als de zwaartekracht: ܹ௪௥ = − 0,10 ∙ 500 ∙ 8 = − 400 J.
De netto arbeid is dan: W = 2000 – 150 – 400 = 1450 J.
ଶௐ
Uit ܹ = ∆భమ௠௩ మ met beginsnelheid 0 volgt nu: ‫ݒ‬௘௜௡ௗ = ට ௠ = ට
ଶ∗ଵସହ଴
ହ଴
= 7,6 m/s.
N.B. Je kunt ook alles uitrekenen zonder energieën te gebruiken. Je bepaalt dan eerst de resultante
kracht op de helling (component van de zwaartekracht langs het vlak min de wrijvingskracht (400-30
=370 N); deelt door de massa om de versnelling a te krijgen (7,4 m/s2), berekent met ‫ݏ‬ሺ‫ݐ‬ሻ = భమܽ‫ ݐ‬ଶ de
tijd die nodig is voor de afdaling (1,16 s) en dan met ‫ݒ‬ሺ‫ݐ‬ሻ = ܽ‫ ݐ‬de snelheid beneden (8,60 m/s).
Vervolgens bepaal je voor het horizontale deel de resultante kracht (alleen de wrijvingskracht, - 50 N),
weer de versnelling a (-1,0 m/s2) en met ‫ݏ‬ሺ‫ݐ‬ሻ = ‫ݒ‬ሺ0ሻ‫ ݐ‬+ భమܽ‫ ݐ‬ଶ de benodigde tijd (0,987 s) en met
‫ݒ‬ሺ‫ݐ‬ሻ = ‫ݒ‬ሺ0ሻ + ܽ‫ ݐ‬de eindsnelheid (7,6 m/s).
Bu, december 2010
Pagina 1