Werkles Ruimtevaart Heelal e)

Werkles Ruimtevaart
Heelal e)
1) Het internationale ruimtestation ISS dat rond de aarde cirkelt, is afgeleid van
de ideeën van de Duits-Amerikaanse raketgeleerde Wernher von Braun. Deze
ontwierp rond 1950 een wielvormig ruimtestation.
We gaan er in het vervolg van deze opgave vanuit dat dit ruimtewiel ook
werkelijk gerealiseerd is en op 1730 km hoogte in een cirkelvormige baan rond
de aarde draait. Voor de baansnelheid v van een ruimteobject dat in een
cirkelbaan met straal r om de aarde draait, geldt:
v
a) Leid dit af.
b) Bereken de omlooptijd van het ruimtewiel rond de aarde, in uren.
GM aarde
r
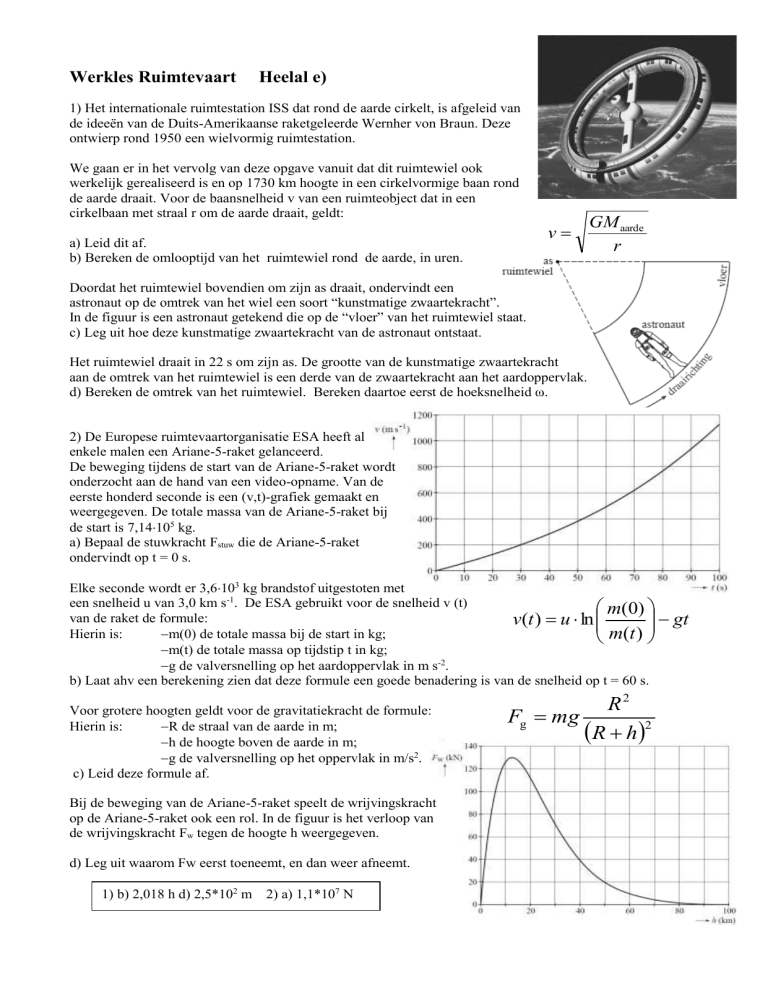
Doordat het ruimtewiel bovendien om zijn as draait, ondervindt een
astronaut op de omtrek van het wiel een soort “kunstmatige zwaartekracht”.
In de figuur is een astronaut getekend die op de “vloer” van het ruimtewiel staat.
c) Leg uit hoe deze kunstmatige zwaartekracht van de astronaut ontstaat.
Het ruimtewiel draait in 22 s om zijn as. De grootte van de kunstmatige zwaartekracht
aan de omtrek van het ruimtewiel is een derde van de zwaartekracht aan het aardoppervlak.
d) Bereken de omtrek van het ruimtewiel. Bereken daartoe eerst de hoeksnelheid ω.
2) De Europese ruimtevaartorganisatie ESA heeft al
enkele malen een Ariane-5-raket gelanceerd.
De beweging tijdens de start van de Ariane-5-raket wordt
onderzocht aan de hand van een video-opname. Van de
eerste honderd seconde is een (v,t)-grafiek gemaakt en
weergegeven. De totale massa van de Ariane-5-raket bij
de start is 7,14105 kg.
a) Bepaal de stuwkracht Fstuw die de Ariane-5-raket
ondervindt op t = 0 s.
Elke seconde wordt er 3,6103 kg brandstof uitgestoten met
een snelheid u van 3,0 km s-1. De ESA gebruikt voor de snelheid v (t)
 m(0) 
van de raket de formule:
  gt
v(t )  u  ln 
Hierin is:
m(0) de totale massa bij de start in kg;
m
(
t
)


m(t) de totale massa op tijdstip t in kg;
g de valversnelling op het aardoppervlak in m s-2.
b) Laat ahv een berekening zien dat deze formule een goede benadering is van de snelheid op t = 60 s.
Voor grotere hoogten geldt voor de gravitatiekracht de formule:
Hierin is:
R de straal van de aarde in m;
h de hoogte boven de aarde in m;
g de valversnelling op het oppervlak in m/s2.
c) Leid deze formule af.
Bij de beweging van de Ariane-5-raket speelt de wrijvingskracht
op de Ariane-5-raket ook een rol. In de figuur is het verloop van
de wrijvingskracht Fw tegen de hoogte h weergegeven.
d) Leg uit waarom Fw eerst toeneemt, en dan weer afneemt.
1) b) 2,018 h d) 2,5*102 m 2) a) 1,1*107 N
R2
Fg  mg
R  h 2