1 Meerkeuzevragen met slechts één juist antwoord

Evaluatie druk p.1
DRUK
1 Meerkeuzevragen met slechts één juist antwoord
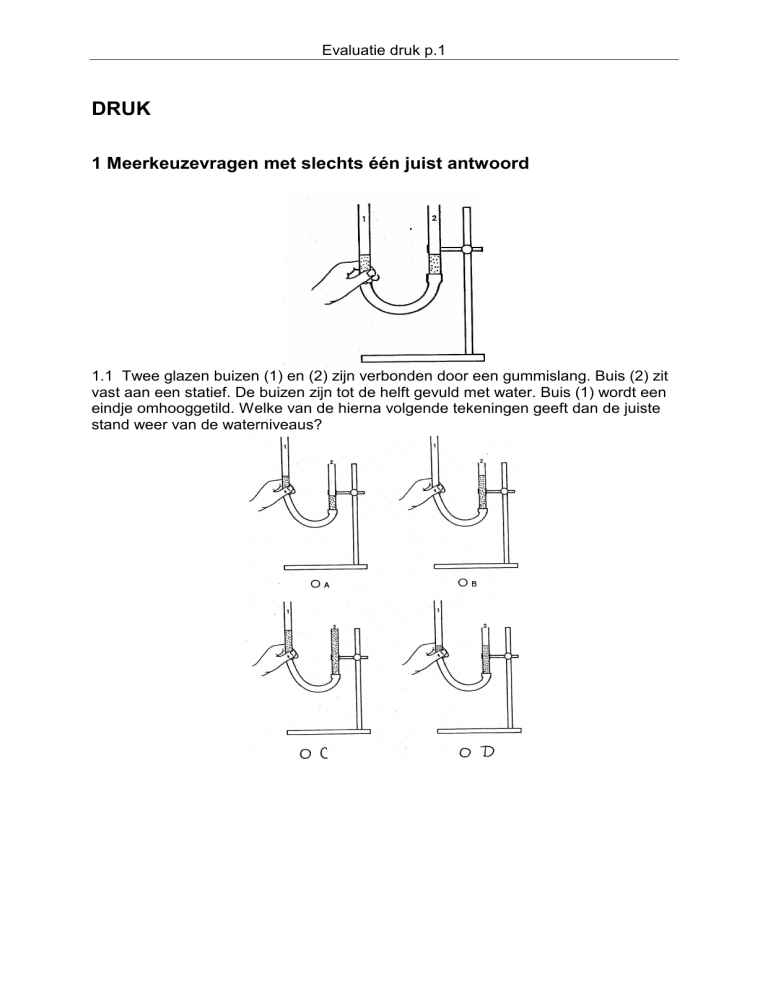
1.1 Twee glazen buizen (1) en (2) zijn verbonden door een gummislang. Buis (2) zit
vast aan een statief. De buizen zijn tot de helft gevuld met water. Buis (1) wordt een
eindje omhooggetild. Welke van de hierna volgende tekeningen geeft dan de juiste
stand weer van de waterniveaus?
Evaluatie druk p.2
1.2 Een U-vormige buis bevat drie niet mengbare vloeistoffen A, B en C.
Uit de figuur kan je over de massadichtheid van de vloeistoffen besluiten dat:
A. ρA < ρB < ρC
B. ρB < ρA < ρC
C. ρA < ρC < ρB
D. ρC < ρA < ρB
1.3 Op nevenstaande figuur drukt het kwik tegen de onderkant van een kraan k.
Indien we de kraan opendraaien dan:
A. zal het kwik uit de buis spuiten.
B. zal het kwik in de buis op dezelfde hoogte komen als in de bak.
C. zal het kwikniveau in de buis niet veranderen.
D. zal er over het kwikniveau in de buis niets kunnen gezegd worden omdat de
atmosferische druk niet gegeven is.
1.4 Een kolf is gevuld met chloroform (dichtheid: 1,5 g/cm3) tot een hoogte h. In een
erlenmeyer bevindt zich ether (dichtheid: 0,75 g/cm3) tot een zelfde hoogte h. De
hydrostatische druk op de bodem van de kolf met chloroform is:
Evaluatie druk p.3
A.
Twee maal groter dan de hydrostatische druk op de bodem van de
erlenmeyer met ether.
B. Twee maal kleiner dan de hydrostatische druk op de bodem van de
erlenmeyer met ether.
C. Even groot als de hydrostatische druk op de bodem van de erlenmeyer met
ether.
D. Deze vraag is niet te beantwoorden: het hangt af van het oppervlak van de
bodem van de kolf en de erlenmeyer.
1.5 Men meet in een vat waarin zich twee verschillende niet mengbare vloeistoffen
bevinden, de hydrostatische druk p bij toenemende diepte h. Uit de onderstaande
grafiek kunnen we afleiden dat in dit geval:
A. dichtheid vloeistof A < dichtheid vloeistof B
B. dichtheid vloeistof A > dichtheid vloeistof B
C. dichtheid vloeistof A = dichtheid vloeistof B
D. deze situatie is onmogelijk
1.6 Men meet in twee vaten die met vloeistof gevuld zijn, de druk p in functie van de
diepte h.
Dit levert de onderstaande grafiek op. Hieruit kun je besluiten dat:
A.
B.
C.
D.
dichtheid vloeistof A < dichtheid vloeistof B
dichtheid vloeistof A > dichtheid vloeistof B
de vloeistofkolom bij B het hoogst is
de atmosferische druk op B het grootst is
Evaluatie druk p.4
1.7 Hier zie je 3 vaten.
Alle vaten hebben hetzelfde grondvlak. In alle vaten giet men een zelfde massa van
dezelfde vloeistof. Dan is de hydrostatische kracht op de bodem het grootst voor:
A. vat a
B. vat b
C. vat c
D. voor alle vaten even groot
1.8 Hier zie je 3 vaten.
Alle vaten hebben hetzelfde grondvlak. In alle vaten giet men tot dezelfde hoogte
dezelfde vloeistof. Dan is de hydrostatische kracht op de bodem het grootst voor:
A. vat a
B. vat b
C. vat c
D. voor alle vaten even groot
1.9 Gegeven een open vat gevuld met vloeistof. Eveneens gegeven is de druk in de
punten a en b aangeduid in de bijgaande figuur.
De massadichtheid van de vloeistof in het vat is ongeveer/
A. 90 kg/m3
B. 180 kg/m3
C. 900 kg/m3
D. 1800 kg/m3
1.10 Men giet vloeistof A in een cilindervormig vat met diameter d tot een hoogte h1.
Om in een vat met diameter d/2 een zelfde hydrostatische druk te bekomen moet
men het vat vullen met vloeistof A tot een hoogte h2 waarbij:
Evaluatie druk p.5
A.
B.
C.
D.
h1 = h2
h1 = 2 h2
2 h1 = h2
geen van de vorige mogelijkheden.
1.11 Het doel van het gebruik van een hydraulische pers is:
A. een kleine druk omzetten in een grote druk
B. een kleine kracht omzetten in een grote kracht
C. een grote druk omzetten in een grote kracht
D. drukken te meten
1.12 Wat gebeurt er met de druk uitgeoefend door een kubus, die op een van zijn
zijvlakken op de tafel rust, als we de afmetingen van de kubus verdubbelen maar wel
hetzelfde materiaal gebruiken.
A. de druk halveert
B. de druk wordt 4x groter
C. de druk wordt 4x kleiner
D. de druk verdubbelt
1.13 We meten eerst de overdruk in een gasleiding met een open manometer
gevuld met water en daarna met open manometer gevuld met alcohol. Het
hoogteverschil tussen de vloeistofspiegels in beide benen is dan:
A. het grootst bij de manometer gevuld met water
B. het grootst bij de manometer gevuld met alcohol
C. in beide manometers even groot
D. niet te bepalen omdat de luchtdruk niet gekend is
1.15 Bekijk de onderstaande figuur.
A.
B.
C.
D.
E.
De druk in punt a is gelijk aan de druk in punt b.
De druk in punt c is gelijk aan de druk in punt d.
De druk in punt e is gelijk aan de druk in punt f.
De druk in punt b is hoger dan 101 300 Pa.
Het drukverschil tussen de punten a en c is 98 Pa indien het niveauverschil
tussen de twee wateroppervlakken 1,0 cm bedraagt.
1.16 De luchtdruk op de top van een berg is:
A. hoger dan de luchtdruk in het dal
B. lager dan de luchtdruk in het dal
C. gelijk aan de luchtdruk in het dal
D. deze vraag kan niet beantwoordt worden
Evaluatie druk p.6
2 Juist of foutvragen met verklaring
2.1 Hydrostatische druk wordt uitgeoefend door vloeistoffen en vindt zijn oorzaak in
de zwaartekracht.
2.2 Hoe groter de dichtheid van de vloeistof, hoe groter de hydrostatische druk.
2.3 Aan duikers leert men dat de druk in het water stijgt met ongeveer 1 bar per 10
m.
2.4 De druk op de bodem van een vat af van de volgende grootheden:
- de grootte van de bodem
- het volume vloeistof in het vat
- de hoogte van de vloeistof in het vat
- de massa van de vloeistof in het vat
- de massadichtheid van de vloeistof
2.5 De hydrostatische druk op een bepaalde diepte h hangt af van de atmosferische
druk.
2.6 De hydrostatische druk op een bepaalde diepte h hangt af van de
massadichtheid van de vloeistof.
2.7 De hydrostatische druk op een bepaalde diepte h hangt af van de vorm van het
vat waar de vloeistof inzit.
2.8 In een zwembad is de totale druk in het water op een diepte 2h dubbel zo groot
als de totale druk op een diepte h.
2.9 In een U-vormige buis is er evenwicht tussen verschillende vloeistoffen.
(massadichtheid gegeven)
2.10 “Duiker A bevindt zich op 10 m onder de zeespiegel. Duiker B op 20 m. Duiker
B ondervindt een druk die dubbel zo groot is als de druk die Duiker A ondervindt.”
2.11 “Thuis kook je een eitje gaar in een zestal minuten; boven op een hoge berg
duurt het heel wat langer”
2.12 Als we bij de proef van Torricelli een buis met dubbele doorsnede nemen, dan
halveert de hoogte van de kwikkolom.
2.13 Als de Maagdenburgse halve bollen perfect gasledig zijn, is het totaal
onmogelijk om ze uit elkaar te trekken.
2.14 De druk in een vloeistof op een diepte 2d is dubbel zo groot als de druk in de
vloeistof op een diepte d.
Evaluatie druk p.7
3 Reproductievragen
3.1 Wat is de Archimedeskracht en hoe hebben we die kracht in de klas
aangetoond?
3.2 Bewijs de volgende uitspraak: "In een U-vormige buis gevuld met 2 niet
mengbare vloeistoffen A en B staan de vrije vloeistofoppervlakken in beide benen
niet even hoog."
3.3 Vervolledig de tekening.
3.4 Geef het essentiële verschil tussen het ontstaan van de hydrostatische druk in
een vloeistof en de druk in gassen.
3.5 Bespreek de proef van Torricelli
A. Maak een tekening.
B. Verklaar het verschijnsel
C. Hoe kan je hieruit de luchtdruk berekenen?
3.6 Een open vloeistofmanometer is aangesloten op een kolf gevuld met een gas.
a. Wat gebeurt er als de gasdruk kleiner is dan de atmosferische druk ? Leg uit en
maak een schets.
b. Hoe kun je de gasdruk in dat geval berekenen?
3.7 Beschrijf de proef van Torricelli. Wat nemen we waar als de atmosferische druk
de normwaarde heeft? Bereken uit deze proef de normale atmosferische druk.
3.8 Wat gebeurt er met een klein opgeblazen ballonnetje onder de vacuümklok?
3.9 We sluiten de deur van een diepvrieskast.
We kunnen ze niet onmiddellijk openen omdat pg … patm
Dit noemt men... druk.
3.10 We vullen de tweehalzige fles tot boven met water.
Evaluatie druk p.8
De twee halzen worden met een kurk afgesloten zodat ze in contact zijn met het
water. Op een van de kurken geven we een korte hamerslag. De andere kurk springt
eruit. (zie figuur)
Welk beginsel wordt hier geïllustreerd? Geef dit beginsel.
3.11 Wat is de hydrostatische druk?
3.12 Geef de werking van verbonden vaten.
3.12 figuur 8
Gegeven is het schema.
a)Wanneer komt het plaatje los?
b)Stel de formule op voor de hydrostatische druk in een punt p op een diepte h in
een vloeistof met massadichtheid ρ.
c)Controleer de eenheden.
3.13 Beschrijf de proef met de Maagdenburgse halve bollen. Welk natuurkundig
verschijnsel wordt hiermee aangetoond?
Evaluatie druk p.9
4 Grafieken
4.1 Een glazen trechter is onderaan afgesloten met een gummivlies en wordt
verbonden met een U-vormige buis, die gedeeltelijk gevuld is met gekleurd water. De
trechter wordt geleidelijk dieper in een bak water gedompeld en op een vijftal dieptes
(h) wordt telkens het bijhorende niveauverschil (∆h) tussen de vloeistofoppervlakken
in de U-vormige buis afgelezen. (zie figuur)
30
∆h (mm)
23
60
45
90
69
120
91
150
118
h (mm)
Wat is het doel van deze proef? (∆h een maat is voor ….?)
In de tabel vind je een aantal meetresultaten: teken de overeenkomstige grafiek.
Welke grafiek bekom je?
Wat is bijgevolg het wiskundig verband tussen ∆h en h?
Welke berekeningen moet je doen om dit te controleren? (in de 3de kolom van de
tabel) Tot welk besluit kom je uiteindelijk? Formuleer dit in woorden!
4.2 Welk diagram geeft het verloop van de hydrostatische druk met de diepte weer in
een vat gevuld met een vloeistof?
4.3 Je wil op een oppervlak A een constante druk uitoefenen. Welke grafiek geeft
het juist verband weer tussen kracht en oppervlakte?
Evaluatie druk p.10
4.4 Bij een experiment werd de hydrostatische druk gemeten op verschillende
diepten in olie en in water. De meetresultaten staan in onderstaande tabel:
H (m)
0,50
1,00
1,50
2,00
2,50
P (hPa) in water
49,1
98,1
147
196
245
P (hPa) in olie
45,0
90,1
135
180
225
a. Stel de grafiek op.
b. Welk verband tussen druk en diepte kun je hieruit afleiden?
c. Hoe zou de grafiek er uitzien (niet tekenen !) indien niet de hydrostatische, maar
de totale druk was gemeten?
4.5 In een open vat gevuld met een vloeistof (dichtheid 0,75 g/cm³) meten we de
hydrostatische druk op verschillende diepten.
a. Teken (algemeen) de grafiek die het verband weergeeft tussen de hydrostatische
druk p en de diepte h in het blauw.
b. Teken op hetzelfde rooster de grafiek die het verband weergeeft tussen de totale
druk in die vloeistof en de diepte h in het zwart.
c. Teken op hetzelfde rooster de grafiek die het verband weergeeft tussen de
hydrostatische druk in een vloeistof met dichtheid: 1,5 g/cm3 en de diepte h in het
groen.
4.6 Gegeven volgende grafiek.
druk (kPa)
400
300
200
100
0
0
5
10
15
20
diepte (m)
Bepaal de hydrostatische druk op een diepte van 13 m.
25
Evaluatie druk p.11
4.7 Teken in een diagram (p, H) de juiste voorstelling voor de druk in functie van de
diepte in een vloeistof.
Construeer nauwkeurig de grafiek die voorstelt: de totale druk p (verticale as) in een
vloeistof in functie van de diepte h (horizontale as). De vloeistof heeft een
massadichtheid van 1,8.103 kg/m3. Vergeet niet dat bij diepte h = 0 m, de totale druk
gelijk is aan de atmosferische druk (1013 hPa)
Evaluatie druk p.12
5 Rekenvragen
5.1 Een walvis heeft een totale huidoppervlakte van 200 m2. Hij duikt bliksemsnel
van een diepte van 5,0 m onder de zeespiegel naar een diepte van 200 m. Bereken
de druk en de drukkracht verandering die hierdoor ontstaat? Je begrijpt meteen,
waartoe de meer dan 30 cm dikke speklaag van de blauwe vinvis dient: niet alleen
als bescherming tegen de kou, maar als een zeer efficiënte bumper!
5.2 Het venster van je studeerkamer geeft uit op de tuin en is 150 dm² groot. Stel
dat de luchtdruk 1018 mbar bedraagt.
Hoe groot is dan de kracht die langs buiten op het venster wordt uitgeoefend? Hoe
komt het dat het raam niet breekt onder invloed van deze grote kracht?
5.3 Een stuk tuinslang is gedeeltelijk met water gevuld. Persoon 1 blaast aan één
uiteinde zodat het niveauverschil tussen beide waterniveaus 1,0 m bedraagt (zie
figuur).
Hoe hard (= met welke druk) blaast hij in de tuinslang? De atmosferische druk
bedraagt op dat ogenblik 1030 hPa.
5.4 Een cilinder met een los bodemplaatje wordt ondergedompeld in een bak met
water, zoals op de figuur getekend is. Je giet voorzichtig benzine in de cilinder.
Tot op welke hoogte moet je de benzine minstens gieten opdat het bodemplaatje zou
loskomen. De massa van het bodemplaatje is te verwaarlozen.
De massadichtheid van de benzine is 660 kg/m³.
Evaluatie druk p.13
5.5 Het hoogteverschil ab bedraagt 30,0 cm olie. De atmosferische druk is 1000
hPa.
5,00 l van een gas X bevinden zich bij 60,0°C in het vat.
Hoeveel moleculen telt het gas? Bereken het normvolume van dit gas. ρolie = 800 kg
/m3
5.6 Een barkruk weegt 70,0 N en rust op 3 poten. Het steunvlak van één poot is een
cirkel met een diameter van 5,00 cm. Hoeveel vergroot de druk op de vloer wanneer
een persoon van 85,0 kg op de kruk gaat zitten.
Als je het vorige vraagstuk niet kon oplossen, kan je nog de helft van de punten
krijgen voor het correct oplossen van het volgende vraagstuk:
Men slaat met een kracht van 250 N met een hamer op een spijker, waarvan de punt
een oppervlakte van 0,250 mm² heeft. Met welke druk (in Pa) wordt de spijker in het
hout gedreven?
5.7 Een gashouder wordt aangesloten op een open vloeistofmanometer die met
water gevuld is. In het open been staat het water 7,2 cm hoger. De atmosferische
druk bedraagt1025 hPa.
a. Bereken de gasdruk
b. De atmosferische druk stijgt tot 1040 hPa. Wat zal er gebeuren met het
hoogteverschil tussen de vloeistofniveaus in de manometer. Bereken het nieuwe
hoogteverschil.
Evaluatie druk p.14
5.8 De druk in een olieveld op 2,00 km diepte is 2,00.107 Pa. Hoe hoog moet de zuil
boormodder die deze druk in bedwang kan houden minstens zijn als de dichtheid van
modder 1,90 g/cm³ bedraagt.
5.9 Een open vloeistof manometer, gevuld met gekleurd water, wordt aangesloten
op een gaskraan van het lab. Als de gaskraan geopend wordt, daalt het vloeistofpeil
in het been dat met de gaskraan verbonden is 11,0 cm. Bereken de overdruk van het
gas in de kraan.
5.10 Bereken de hydrostatische druk van 4,0 km diepte in zeewater (p = 1030 kg /
m³)
5.11 Een meisje van 580 N staat op ski’ s met elk een oppervlakte van 90 cm².
Bereken de uitgeoefende druk op de sneeuw.
5.12 Een slee met twee personen oefent een totale druk uit op de sneeuw van
4048,5 Pa. Het oppervlak van de slee, dat met de sneeuw in contact staat, heeft een
lengte van 90 cm en een breedte van 35 cm. De lege slee oefent op de sneeuw een
druk uit van 311,4 Pa. Een persoon stapt af en oefent op de sneeuw een druk uit van
24525 Pa. Het oppervlak van één schoen bedraagt 120 cm². Bereken de massa van
de persoon die nog op de slee zit.
5.13 In een dolfinarium, gevuld met zeewater met een massadichtheid van 1020
kg/m³, zijn de ruiten 2,00m lang, 1,00 m hoog en 7,00 cm dik. De onderrand bevindt
zich op een diepte van 3,50 m. Hoe groot is de hydrostatische druk op de ruit?
5.14 figuur 9
Aan het linkerbeen van een open vloeistofmanometer wordt een glazen kolf gesloten,
waarin een gas zit. Bij een omgevingsdruk van 1025 hPa staat het waterniveau in de
linkerbuis 7,0 cm lager dan in de rechterbuis.
a)Bereken de druk van het gas in de kolf.
b)Indien de omgevingsdruk plots stijgt tot 1045 hPa, wat gebeurt er dan met de
vloeistofniveaus?
5.15 In een U-buis staat kwik (13,6.103 kg/m3). Daarboven staat in het ene been 24,0
cm water. Hoeveel cm ether (750 kg/m3) moet men in het andere been gieten opdat
de bovenvlakken in een zelfde horizontaal vlak zouden liggen?
Evaluatie druk p.15
6 Inzicht
6.1 Een lichaam wordt ondergedompeld in water (ρ = 1000 kg/m3) en heeft een
volume van 11 cm3. Zal het zinken, zweven of drijven in het water als je weet dat het
voorwerp een massa heeft van 15 g? Waarom?
6.2 Een hotel aan zee heeft zijn zwembad gevuld met zeewater. Vergelijk de
hydrostatische druk op 1 m diepte met de hydrostatische druk op dezelfde diepte in
een ander zwembad dat gevuld is met zuiver water. Speelt de grootte van het
zwembad hier een rol? Verklaar.
6.3 Je moeder heeft aardbeienconfituur gemaakt en giet de hete confituur in glazen
potten. De potten worden onmiddellijk luchtdicht afgesloten met een schroefdeksel.
Een week later wil je wel eens proeven, maar je krijgt de pot niet open. Waarom?
6.4 Een vatenstelsel met communicerende vaten is in evenwicht. Het middelste vat
wordt afgesloten. Aan één kant wordt er water bijgegoten.
Hoe staat het water in het stelsel als er weer evenwicht is?
6.5 Een visser heeft een laars aan een haak geslagen. Verklaar waarom de vislijn
pas sterk zal doorbuigen bij het ophalen van de laars uit het water.
6.6 Waarom snijdt een mes beter als het goed geslepen is?
6.7 Gegeven: 3 vaten zijn respectievelijk gevuld met water, ethanol en kwik.
Rangschik deze vaten volgens stijgende hydrostatische druk op de bodem van het
vat. Motiveer je antwoord.
6.8 figuur 10
Dit vat is tot aan de bovenrand gevuld met water. Bereken de druk door de vloeistof
uitgeoefend in de punten a en b.
Evaluatie druk p.16
(massadichtheid water: 998 kg/m3)
6.9 Leg uit hoe het komt dat, als je met een grote kracht een duimspijker in een
muur duwt, je nauwelijks iets voelt van die kracht.
6.10 Verklaar waarom een zuignapje niet gemakkelijk loslaat (of van de wand valt).
6.11 Tot welke hoogte zou de vloeistof in de buis van Torricelli komen bij normale
atmosferische druk, als deze buis met water is gevuld? (massadichtheid water =...)
(massadichtheid kwik =...)
6.12 Waarom legt men om de 50 cm dwarsliggers onder de treinrails?
6.13 Drijft lood op kwik? ρHg = 13590 kg/m³ ρPb = 11300 kg/m³
6.14 Enkel met landbouwmachines met rupsbanden kan men over natte akkers
rijden. Leg dit uit met het begrip druk.
6.15 Welk spijkerbed zal de fakir verkiezen: een bed met veel spijkers of een bed
met weinig spijkers?
Evaluatie druk p.17
7 Doevragen of opdrachtvragen
7.1 De druk van het gas in de gasleiding meten met een vloeistofmanometer en
daaruit de gasdruk in hPa bepalen.
7.2 Lees de barometerdruk af in cm en in Pascal. Waarom is de afgelezen waarde
niet gelijk aan de normale atmosferische druk.
Evaluatie druk p.18
ARBEID, ENERGIE EN VERMOGEN
1 Meerkeuzevragen met slechts één antwoord
1.1 Op een voorwerp kunnen vier verschillende krachten aangrijpen. Het verband
tussen grootte van de kracht en de verplaatsing voor deze gevallen is hieronder
weergegeven. In welk diagram staat de kracht die het meest arbeid geleverd heeft?
1.2 Een wagentje van 1000 kg legt op de foor de weg af, die hieronder getekend is.
Als het wagentje in punt a uit rust vertrekt en als de wrijving te verwaarlozen is, wat is
dan juist?
A. De kinetische energie van het wagentje zal groter zijn in punt c dan in punt b.
B. De kinetische energie van het wagentje zal kleiner zijn in punt b dan in punt c.
C. Het wagentje zal stilvallen in punt c.
D. Het wagentje zal nooit in punt c aankomen.
a
b
c
1.3 In welke van onderstaande grafieken staat de kracht die het meest arbeid
geleverd heeft.
Evaluatie druk p.19
1.4 De wet van behoud van energie betekent dat:
A.
B.
C.
D.
ieder lichaam waarop geen kracht werkt steeds uit zichzelf tot rust komt.
de som van de kinetische en de potentiële energie steeds gelijk blijft.
de som van de kinetische en de potentiële energie steeds nul is.
de kinetische energie steeds gelijk blijft aan de potentiële energie.
1.5 Het rendement van een hydro-elektrische centrale is 80 %. Dit betekent dat:
A. 80 % van de potentiële energie van het water uit het stuwmeer omgezet wordt
in elektrische energie en dat 20 % ervan wordt omgezet in warmte.
B. 80 % van de potentiële energie van het water uit het stuwmeer omgezet wordt
in warmte en dat 20 % ervan wordt omgezet in elektrische energie.
C. 80 % van de potentiële energie van het water uit het stuwmeer omgezet wordt
in elektrische energie en dat 20 % ervan wordt omgezet in kinetische energie
van het vallende water.
1.6 Gegeven: twee vrachtwagens A en B. De massa van vrachtwagen B is dubbel
zo groot als de massa van A en B rijdt met een snelheid die dubbel zo groot is als de
snelheid van A. Wat weet je over de kinetische energie van deze vrachtwagens?
Evaluatie druk p.20
A.
B.
C.
D.
E.
Ek, B = 2 Ek,A
Ek, B = 4 Ek,A
Ek, B = 6 Ek,A
Ek, B = 8 Ek,A
Ek, B = 16 Ek,A
1.7 Wanneer we beroep doen op een mechanisch werktuig om een bepaald karwei
op te knappen, dan moeten we:
A. meer arbeid leveren
B. minder arbeid leveren
C. evenveel arbeid leveren
D. is afhankelijk van het soort werktuig
1.8 We hebben vier verschijnselen:
1 het rollen van een biljartbal over het laken
2 het dalen van een parachutist
3 het omhoog werpen van een bal
4 het wegrijden van een auto op een horizontale weg
De potentiële energie verandert bij:
A. 1 en 2
B. 3 en 4
C. 2 en 3
D. 1 en 4
1.9 Wanneer vergroot de potentiële energie?
A. bij het vallen van een regendruppel
B. bij het omhoog gaan van een weggeschoten pijl
C. bij het rollen van een bal over een horizontaal oppervlak
D. in geen enkele van de gegeven situaties
1.10 Een massa van 508 g valt in 3,0 s van een hoogte van 18 m verticaal op de
grond. Van welke hoogte moet een massa van 254 g vallen opdat de zwaartekracht
dezelfde arbeid zou leveren?
A. 9,0 m
B. 36 m
C. 72 m
D. Niet te berekenen met deze gegevens
1.11 Als het vermogen van motor A groter is dan het vermogen van motor B dan
betekent dit dat:
A. motor A meer arbeid levert dan B
B. motor A een grotere snelheid haalt dan B.
C. motor A meer kracht levert dan B.
D. geen van de vorige antwoorden is juist.
Evaluatie druk p.21
2 Juist of foutvragen met verklaring
2.1 Een arbeider die een zak cement 3 m hoog draagt, levert arbeid.
2.2 Een arbeider die met een zak cement 3 m hoog op een ladder staat, levert
arbeid.
2.3 Een arbeider die een zak cement in 2 minuten naar boven draagt, heeft een groter vermogen dan
zijn collega die daar 1 minuut voor nodig heeft.
2.4 1 kWh is een eenheid van vermogen.
2.5 Tussen de eenheden van kracht, arbeid en vermogen gelden volgende
verbanden:
a. 1 J = 1 N/m
b. 1 W = 1 J.s
2.6 Iemand staat met een boekentas van 10,0 kg 10 minuten onbeweeglijk te
wachten aan een bushalte. De persoon levert 59.103J arbeid.
2.7 Een ophaalkraan verricht een arbeid van 36.105J om een massa van 4000 kg op
te tillen. De hoogte waarover het voorwerp verplaatst is bedroeg 92 m.
2.8 Een gewichtheffer die een halter niet kan opheffen verricht geen arbeid.
2.9 Drie personen duwen om beurt tegen een auto. De eerste persoon duwt hem, in
3 minuten, 10 m ver; de tweede duwt hem, in 5 minuten, 10 m ver; de derde
verplaatst hem niet. Zijn volgende uitspraken juist of fout?
a. Ze oefenden alle drie dezelfde arbeid uit.
b. Enkel de eerste twee oefenden een kracht uit.
c. De eerst twee oefenden dezelfde kracht uit, maar het vermogen van de
eerste is groter.
d. Het vermogen en de arbeid van de derde is nul, maar zijn kracht niet.
2.10 Men levert arbeid op een auto als men hem duwt enkel en alleen als hij ook in
beweging komt.
2.11 Het rendement van een machine vergroot naarmate er minder energie moet
ingestopt worden.
2.12 Als men een kracht van 25 N verticaal naar boven laat inwerken op een
voorwerp van 10 kg, dan wordt er positieve arbeid uitgeoefend door die kracht op dat
voorwerp.
Evaluatie druk p.22
3 Reproductievragen
3.1 Je duwt tegen een zware kast en ze verschuift 5 cm. Verricht je dan arbeid?
Verklaar.
3.2 Wat versta je onder 1 kWh? Waarvan is dit een eenheid? Toon aan.
3.3 Een waterval is 25 m hoog. Gemiddeld valt er 20 ton water per seconde naar
omlaag. Hoeveel arbeid levert de zwaartekracht in 1,0 uur op dat water? Welke
energieomzettingen gebeuren er tijdens het vallen van het water? Verklaar. Wat
gebeurt er tijdens deze omzettingen met de totale energie?
3.4 Toon aan dat een hydraulische pers een werktuig is en dat de wet van behoud
van arbeid geldig is.
3.5 Wat is het essentiële verschil tussen energie en arbeid? Bespreek
3.6 Wanneer bezit een lichaam energie? Definieer twee vormen van mechanische
energie en geef de formule. Formuleer de wet van behoud van energie. Wanneer
heeft een machine een vermogen van 1 watt?
3.7 Beschrijf de beweging van het wiel van Maxwell en stel de energieomzettingen
voor.
3.8 Leid de formule af van de arbeid verricht bij het uitrekken van een veer.
3.9 Omschrijf: inwendige energie
3.10 Welke energieomzettingen gebeuren bij het branden van een kaars?
3.11 Over welke energievormen gaat het in de volgende beschrijvingen? (Vermeld voor de
berekeningen enkel de formule en het resultaat.)
Men heft een boekentas van 10 kg 0,80 m hoog. Energievorm:
Grootte van de energie van de boekentas:
Men stapt met die boekentas in de hand aan een snelheid van 2 m/s. Energievorm:
Grootte van de energie van de boekentas:
3.12 Bespreek de energieomzettingen die optreden bij het verticaal afschieten van
een pijl tot hij terug de grond raakt. Als men geen rekening houdt met de wrijving en
de luchtweerstand, wat weet je dan van de snelheid waarmee hij de grond raakt?
Welke wet pas je hier toe?
3.13 Stel de energiebalans op van het wiel van Maxwell (in een gesloten stelsel).
Wees volledig in je uitleg.
3.14 Toon aan dat een hydraulische pers een werktuig is en dat de wet van behoud
van arbeid geldig is.
3.15 Wat is het essentiële verschil tussen energie en arbeid? Bespreek
Evaluatie druk p.23
3.16 Geef het verband tussen kWh en J.
3.17 Bewijs het behoud van arbeid bij een hydraulische pers.
Evaluatie druk p.24
4 Grafieken
4.1 Vergelijk de arbeid W 1, geleverd door F1 en de arbeid W 2, geleverd door F2. Vul
de vier stippellijnen op de grafiek aan. Welke is de grootste arbeid en waarom?
4.2 Lien duwt een kist vooruit met een kracht, die voorgesteld is op de onderstaande
grafiek. Bereken de arbeid die Lien levert op de kist, wanneer ze de kist 50 m
verplaatst heeft.
F (N)
1000
800
600
400
200
0
0
20
40
60
X (m)
80
Evaluatie druk p.25
4.3 Gegeven volgende grafiek.
kracht (N)
5
4
3
2
1
0
0
50
100
afstand (m)
Bepaal de arbeid door de kracht geleverd.
4.4 Men wil een veer 20 cm uitrekken. Moet men evenveel arbeid verrichten voor de
eerste als voor de tweede 10 cm vervorming? Uitleggen met een F(x)-grafiek.
4.5 Als de arbeid constant is, hoe ziet het (F) ∆x -diagram er dan uit? Teken in het
tweede diagram de arbeid bij een constante kracht en duid aan hoe we daaruit de
arbeid kunnen berekenen. Vul ook de eenheden in bij de grootheden.
F
F
∆X
∆X
Evaluatie druk p.26
5 Rekenvragen
5.1 Hoeveel elektrische energie gebruik je als je een lamp van 60 W gedurende 1,5
h laat branden (in J en in kWh)?
5.2 Hoeveel kost dit als je twee zulke lampen laat branden en het tarief 5,92
BEF/kWh bedraagt?
5.3 De Schotse ingenieur en uitvinder James Watt (1736 - 1819) voerde als eenheid
van vermogen de "pk = paardenkracht" in. In die tijd werd in de mijnen de steenkool
bovengehaald met behulp van paarden. Watt stelde 1 pk gelijk aan het vermogen
van een paard dat per minuut 4500 kg steenkool 1 m omhoog haalt.
5.4 In de jaren 60 zag je veel 2-pk'tjes (eendjes: zie foto) rondtoeren op onze wegen.
De eerste wagentjes van dit type hadden slechts een vermogen van 2 pk. Hoe groot
is dit vermogen, uitgedrukt in SI-eenheden?
5.5 Je ontbijt bestaat uit 30 g cornflakes en 150 g halfvolle melk. Dit ontbijt heeft een
energiewaarde van 700 kJ. Hoeveel treden kan je met behulp van deze energie
oplopen als je veronderstelt dat alle energie van dit ontbijt aan je spieren wordt
overgedragen. Eén trede is 27 cm hoog. Gebruik je eigen massa of kies als massa
65 kg.
5.6 In de kerncentrale van Doel wordt kernenergie omgezet in elektrische energie.
Het rendement van deze omzetting bedraagt 33,4 %? Hoeveel elektrische energie
ontstaat er per seconde, als de kernreactor 3000 MJ kernenergie omzet in 1
seconde?
5.7 Een lift van 600 kg stijgt 5 verdiepingen hoog in 50,0 s. Elke verdieping is 5,00 m
hoog.
Bereken de geleverde arbeid door de motor en het vermogen van de motor.
5.8 Een hijskraan heeft een vermogen van 1,53 kW. In hoeveel tijd kan deze kraan
een hoeveelheid stenen van 1500 kg naar een hoogte van 25 m brengen?
5.9 Welk vermogen heeft een waterkrachtcentrale als er per 1,0 s 3000 ton water 25
m naar beneden valt?
5.10 Hoe hoog moet je een boekentas met een massa van 1325 g optillen om een
arbeid van 10 J te leveren?
Evaluatie druk p.27
5.11 Je tilt een zak cement van 50 kg op tot een hoogte van 1,20 m in een tijd van
3.0 s. Bereken de geleverde arbeid
Bereken de geleverde arbeid als je de zak vasthoudt op 1,20 m.
Bereken je ontwikkeld vermogen om de zak op te heffen tot 1,20 m hoogte. Stel de
geleverde arbeid van vraag grafisch voor.
5.12 Op een strijkijzer wordt een vermogen van 1000 W vermeld. Na een tijdje
strijken lees je op de elektriciteitsmeter af dat 850 kJ energie verbruikt werd. Hoe
lang heeft het strijkijzer aangestaan? Bereken het rendement, als je weet dat 790,5
kJ energie aan het strijkgoed werd afgegeven? Welke energieomzetting gebeurt
hier? Als je weet dat de prijs voor 1 kWh 0.10 € bedraagt, hoeveel kost dan dit
strijkje?
5.13 Een kist van 150 kg wordt over een afstand van 7,0 m naar een tafel
geschoven. Hiervoor was een kracht van 300 N nodig. Daarna werd de kist op een
tafel getild die 0,75 m hoog is. Bereken de totaal geleverde arbeid.
5.14 Een elektrische centrale haalt energie uit een waterbekken dat 400 m hoger
gelegen is. Hoeveel m3 water moeten de turbines per minuut verwerken, met een
rendement van 0,60 % om een vermogen te leveren van 100 MW?
5.15 Een lift van 600 kg stijgt 5 verdiepingen hoog in 50,0 s. Elke verdieping is 5,00
m hoog. Bereken de geleverde arbeid door de motor en het vermogen van de motor.
5.16 Een hijskraan beschikt over een motor met vermogen 30,0 kW. In hoeveel tijd
kan men hiermee een container van 30,0 ton 16,0 m hoog uit het ruim van een schip
optillen als het rendement 72 % bedraagt?
5.17 Koen laat een voetbal van 950 g van op 1,95 m hoogte vallen. Bij het botsen
op de grond gaat er 21 % aan energie verloren. Hoe hoog stuit de bal terug?
Evaluatie druk p.28
6 Inzichtvragen
6.1 Er vinden verschillende energieomzettingen plaats, als je fietsdynamo je
voorlicht doet branden. Stel deze energieomzettingen schematisch voor en geef voor
elke energieomzetting aan waar ze plaats vindt. Start bij je (kuit)spieren.
6.2 Wrijf met je handen over elkaar. Welke energie bezitten je bewegende handen?
Je stopt met wrijven en je houdt je handen stil. Is de energie uit antwoord a) nu
verdwenen? Verklaar!
6.3 Een opgespannen veertje schiet bij het openen van je balpen weg.
Welke energie is verantwoordelijk voor het wegschieten van het veertje? Leg uit
Wat gebeurt er tijdens het afschieten met deze energie? Leg uit.
6.4 Welke energieomzetting heb je bij:
a. verbranden van steenkool
b. opladen van een accu
c. een strijkijzer
d. een speelgoedautootje dat rijdt nadat je het 'opgewonden' hebt.
6.5 Een voorwerp vertrekt uit rust en valt naar beneden (zie figuur). Heeft dit
voorwerp op het moment dat de helft van de valafstand afgelegd is, meer, minder of
evenveel kinetische energie als potentiële energie (wrijving verwaarlozend)?
Verklaar je antwoord.
6.6 Wordt er arbeid verricht in de volgende gevallen en leg je antwoord uit: indien je
in een stoel zit, indien je in de winter met een plastieken zak wrijvingloos glijdt over
ijs
6.7 Welke energieomzettingen gebeuren bij
een batterij
een stuwdam waarbij men een sluisdeur opent
6.8 Pas de definitie van het vermogen toe bij het vergelijken van een lamp van 25 W
met een lamp van 100 W.
6.9 Welke energievormen en welke energieomzettingen treft men aan bij:
• Een brandende kaars?
• Een bergrivier?
• Een kerncentrale?
• Een benzinemotor?
6.10 Een elektrische motor heeft een rendement van 90 %. Wat betekent dit?
6.11 Een gewichtheffer die een halter opheft verricht arbeid.
Evaluatie druk p.29
7 Doevragen
7.1 Uit te voeren in kleine groepjes
Probleemstelling:
Jullie hebben de definitie van het vermogen geleerd. Probeer dit nu toe te passen!
Opdracht: bereken het vermogen van een leerling die de trappen oploopt.
Benodigdheden:
Weegschaal, chronometer, lange meetlat of lintmeter, rekenmachine.
Werkwijze:
De klas wordt verdeeld in groepen. In elke groep wordt één leerling gekozen.
Deze leerling zal straks de trappen (van de brandladder op de speelplaats) oplopen
en haar ontwikkelde vermogen moet berekend worden. Voer de proef voorzichtig uit!
Vooraleer je begint moet je een strategie opbouwen.
De volgende vragen zijn een hulp:
(Let bij de metingen en berekeningen op het aantal beduidende cijfers!)
1°) Welke kracht moet de leerling uitoefenen om zichzelf op te tillen? Hoe kan je
deze kracht berekenen? Welke grootheid moet je meten om deze kracht te kunnen
berekenen?
2°) Hoe bereken je de arbeid die de leerling levert? Welke grootheid moet je nog
meten? Hoe kan je dit met de beschikbare middelen het eenvoudigst doen?
3°) Met welke formule bereken je het vermogen van de leerling? Welke grootheid
moet je nu nog meten? Spreek op voorhand goed af hoe je de meting zo nauwkeurig
mogelijk zal uitvoeren.
7.2 Op twee verschillende veren laat men verschillende krachten inwerken. Deze
krachten geven een verlenging ∆l aan de veren volgens onderstaande tabel.
F in N
1,0
2,0
3,0
4,0
5,0
∆l1 in cm
1,00
1,95
3,02
4,01
5,00
∆l2 in cm
3,10
6,00
8,95
12,0
15,0
Zet uit in een F(∆l) - grafiek. Wat duidt de rico aan?
Bereken de arbeid om elke veer 5,00 cm uit te rekken op 2 verschillende manieren.
Evaluatie druk p.30
GASWETTEN
1 Meerkeuzevragen
1.1 Een bepaalde hoeveelheid van een als ideaal te beschouwen gas ondergaat de
toestandsveranderingen van A → B → C weergegeven op onderstaande grafiek. In C
is het volume 3,0 l (liter). Welk van volgende mogelijkheden is juist voor het volume
in toestand A?
A.
B.
C.
D.
1,5 l
2,5 l
3,0 l
5,0 l
1.2 Welk getal benadert het best het aantal deeltjes in 1 cm³ van een ideaal gas bij
een druk van 8,31.10-11 Pa bij - 173 °C?
A. 105
B. 1019
C. 1024
D. 10-22
E. niet te bepalen, vermits we niet weten over welk gas het gaat.
De volgende gegevens kunnen weggelaten worden of gebundeld met andere
gegevens in het begin van het examen staan: de molaire gasconstante = 8,31
J/mol.K en het getal van Avogadro = 6,02.1023
1.3 Welke van onderstaande grafieken stelt een isochoor proces voor. Verklaar
telkens waarom.
Evaluatie druk p.31
1.4 Welke gaswet geldt er in de volgende gevallen?
1.4.1 We maken een ballon groter door hem onder een luchtklok te plaatsen en de
lucht onder de luchtklok weg te zuigen.
A. drukvolume wet
B. druktemperatuur wet
C. volumetemperatuur wet
D. geen van deze
1.4.2 We maken een ballon groter door CO2 aan de ballon toe te voegen.
A. drukvolume wet
B. druktemperatuur wet
C. volumetemperatuur wet
D. geen van deze
1.4.3 We maken een ballon een klein beetje groter door hem met een haardroger
een klein beetje te verwarmen.
A. drukvolume wet
B. druktemperatuur wet
C. volumetemperatuur wet
D. geen van deze
1.5 De molaire massa van H2-gas is 2,00 g/mol en van O2-gas 32,0 g/mol. Wanneer
we in 2 even grote kolven respectievelijk 2,00 g H2-gas en 2,00 g O2-gas opsluiten en
beide op dezelfde temperatuur brengen, dan is de druk:
A. in beide kolven even groot
B. voor O2-gas 16 maal groter
C. voor O2-gas 16 maal kleiner
D. voor O2-gas 32 maal groter
E. voor O2-gas 32 maal kleiner.
Evaluatie druk p.32
1.6 De toestand van een gas wordt beschreven door de volgende grootheden:
A. p, V, T, F
B. p, T
C. p, V, T
D. V, T, F
1.7 20° C komt overeen met:
A. 273 K
B. 293 K
C. 253 K
D. 20 K
1.8 Bij een isochoor proces op een bepaalde hoeveelheid gas, zal:
A. de druk toenemen en de temperatuur dalen.
B. de druk en de temperatuur toenemen.
C. de druk en de temperatuur constant blijven.
D. de druk dalen en de temperatuur toenemen.
1.9 Een open waterreservoir bevat water tot een diepte van 20 m. De temperatuur
van het water is constant. De atmosferische druk is gelijk aan de druk van een
waterkolom van 10 m hoogte. Een luchtbel vertrekt op de bodem en stijgt tot het
wateroppervlak. Dan zal het volume van de bel:
A. gehalveerd zijn alvorens aan de oppervlakte te komen
B. verdubbeld zijn alvorens ze aan de oppervlakte komt
C. constant blijven
D. gehalveerd zijn alvorens ze 10 m gestegen is
Evaluatie druk p.33
2 Juist of onjuistvragen met verklaring
2.1 Men verwarmt een ideaal gas zonder de druk te veranderen totdat het volume
vier maal groter is. Antwoord met juist of fout en verklaar bondig. “Na de
transformatie is de temperatuur (in K) tweemaal hoger”.
2.2 Je blaast een voetbal op met een pomp. De gaswet van Boyle Mariotte is geldig
tijdens het opblazen. Juist of fout?
2.3 Men verwarmt een ideaal gas zonder de druk te veranderen tot het volume
viermaal groter geworden is. Dan is de absolute temperatuur viermaal kleiner
geworden. Juist of fout?
2.4 Eén mol van een ideaal gas heeft altijd een volume van 22,4 liter.
2.5 Bij gassen mag je de wet van Boyle en Mariotte altijd toepassen, als je de
temperatuur constant houdt.
2.6 Eén mol van een ideaal gas bevat in normomstandigheden 6,023.1023 deeltjes.
2.7 Bij een ideaal gas is het aantal botsingen verwaarloosbaar klein.
2.8 Als voor een constante hoeveelheid ideaal gas de absolute temperatuur
verdubbelt, dan zal de druk eveneens verdubbelen.
2.9 Een verandering van inwendige energie van een stof is steeds waarneembaar
door een temperatuurverandering.
2.10 De universele gasconstante toont aan dat het volume ingenomen door een
zelfde hoeveelheid bij een bepaalde temperatuur en druk afhangt van het soort gas.
2.11 Iemand blaast een ballonnetje op en sluit het daarna af. Geld de wet van Boyle
Mariotte in de volgende gevallen:
Als de persoon het ballonnetje na het opblazen langzaam indrukt
Als de persoon het ballonnetje na het opblazen in de zon legt
2.12 Om een gasvolume bij een constante druk te verdubbelen, moet de
temperatuur verdubbelen.
Evaluatie druk p.34
3 Reproductievragen
3.1 Moleculaire verklaring van de wet van Boyle.
Vul in onderstaande tekst de ontbrekende woorden en berekeningen in.
De druk die door een gas wordt uitgeoefend op de wanden van het vat, waar het gas
zich in bevindt, is het gevolg van de vele ……………………… van de moleculen
tegen de wand. Hoe méér hoe ……………… de druk wordt.
We beschouwen een gas dat geplaatst is in een kubusvormig vat met zijde z1. Per
seconde oefenen de moleculen kracht F1 uit op de wand.
Als we dan de zijden van deze kubus 5 (vijf) maal zo groot maken, dan zal de weg,
die door een molecule wordt afgelegd tussen twee opeenvolgende
……………………… tegen de wand gemiddeld ……… maal zo ………………
worden. Omdat het aantal moleculen niet veranderd is (constante massa) zal de
kracht op de wand dan ook ……… maal zo ……………… zijn.
Gas met massa m, op temperatuur T,
opgesloten in een kubusvormig vat met
zijde z1
Kracht op de wand: ………
Hetzelfde gas, massa m, op temperatuur
T, opgesloten in een kubusvormig vat met
zijde z2 = 5.z1
Kracht op de wand: ………
Oppervlakte van de wand: ………
Oppervlakte van de wand: ………
Druk: ………
Druk: ……………………………
Volume: ………
Volume:…………………………
Product druk x volume: …………
Product druk volume: ……………………
BESLUIT:…………………………
3.2 Formuleer de gaswet van Dalton in woorden.
3.3 Waarom noemt men -273,15 K het absolute nulpunt?
3.4 Geef de moleculaire verklaring voor
a) de volumedruk wet
b) de druktemperatuur wet
c) de volumetemperatuur wet
3.5 Leid de algemene gaswet af door combinatie van de afzonderlijke gaswetten.
3.6 Geef de volumetemperatuur wet (met uitleg bij de gebruikte symbolen). Verklaar
deze gaswet met het deeltjesmodel. Teken de grafiek die bij deze wet hoort. Wat is
de juiste naam voor deze grafiek?
3.7 Geef twee voorbeelden die aantonen dat gassen een kracht uitoefenen.
Evaluatie druk p.35
3.8 Schets het deeltjesmodel van een ideaal gas en vergelijk dit met het
deeltjesmodel van een reëel gas.
Evaluatie druk p.36
4 Grafieken
4.1 Zet volgende p(T)-diagram om in een p(V)-diagram en verklaar.
4.2 Teken (in hetzelfde assenstelsel) twee grafieken (a) en (b) die elk een isobare
toestandsverandering voorstellen van een ideaal gas. De massa van het gas in (a) is
kleiner dan de massa van het gas in (b).
4.3 Een ideaal gas gaat over van toestand a naar toestand b en vervolgens naar
toestand c.
Deze toestandsveranderingen zijn op het onderstaand diagram weergegeven.
Het gas gaat uiteindelijk over van toestand c naar toestand d. Teken toestand d op
dit diagram, zodat de toestandsverandering een isotherm proces is en zodat punt d
op dezelfde isobaar ligt als punt b.
Bereken de druk in toestand b als je weet dat de druk in toestand a 50 kPa bedraagt.
-3
V (10 m³)
12,0
10,0
8,0
6,0
4,0
a
2,0
b
c
T (K)
0,0
0
100 200 300 400 500 600 700 800 900 1000
4.4 Hoe verandert de isotherm op het p(V)-diagram indien de proef van BoyleMariotte bij een andere temperatuur wordt uitgevoerd? Schets en verklaar volledig.
4.5 Een constante hoeveelheid gas, opgesloten in een constant volume V1, wordt
opgewarmd.
a. Teken de grafieken die het verband weergeven tussen druk en temperatuur.
b. Veronderstel dat we dezelfde hoeveelheid gas opsluiten in een kleiner volume V2
en dezelfde proef uitvoeren. Teken opnieuw de grafieken en schrijf er telkens V2 bij.
Evaluatie druk p.37
Figuur
4.6 Welke van de drie onderstaande grafieken stellen een isobare
toestandsverandering voor?
4.7 Onderstaande grafiek geeft het verband weer tussen volume en temperatuur
voor een bepaalde hoeveelheid gas.
V
2
1
0
T
Teken de overeenkomstige grafiek die het verband weergeeft tussen de druk en het
volume van die gashoeveelheid.
4.8 Geef de gaswet in formulevorm die uit deze grafiek af te leiden is.
Welke voorwaarde(n) moet je eraan toevoegen?
Hoe noemen we het verband tussen de druk en het volume?
t2
t1
Vul in: <of>: t3
V
Evaluatie druk p.38
T
Wat stelt deze tekening voor?
Bespreek.
4.9 Een constante hoeveelheid gas doorloopt het kringproces abca. De temperatuur
in a en b is 900 K. Welke processen worden er uitgevoerd?
p
b
c
a
V
4.10 Teken een isobaar proces.
V
p
T
T
4.11 Grafisch werk
figuur 11
Deze figuur hoort bij een ideaal gas. Beschrijf wat er gebeurt met het gas bij de
overgang 1 --> 2 en van 2 --> 3.
4.12 Een kringproces wordt voorgesteld door volgend p(T)-diagram. Toestand a: Va
= 2,00 m3.
Zet het proces uit in een p(V) en V(T)-diagram. Bereken eerst de nodige waarden.
Hoe noemen de 4 processen ab, bc, cd en da?
Evaluatie druk p.39
5 Rekenvragen
5.1 Een luchtbel stijgt van op de bodem van een meer waar het 4,0 °C is naar het
oppervlak waar het 12 °C is. Hierbij verdubbelt het volume. Wat is de druk op de
bodem van het meer als die aan het oppervlak 1013 hPa is en hoe diep is het meer?
5.2 In een meetspuit bevindt zich een hoeveelheid lucht. Met een manometer wordt
de druk in de meetspuit gemeten. (Het inwendige volume van de manometer is
verwaarloosbaar klein t.o.v. het volume van de meetspuit)
Hieronder vind je enkele meetresultaten:
hPa
V m (cm 3)
50
60
p (kPa)
90
75
Wat zal de druk zijn indien het volume van de meetspuit 70 cm³ bedraagt ?
5.3 Een kringproces wordt voorgesteld door volgend p(T)-diagram. Toestand a:
Va=2,00 m3
Zet het proces uit in een p(V) en V(T)-diagram.
Bereken eerst de nodige waarden.
Hoe noemen de 4 processen ab, bc, cd en da?
5.4 4,00 liter van een ideaal gas heeft bij 300 K een druk van 2,00 105 Pa. Het gas
zet eerst uit bij constante druk tot driemaal zijn oorspronkelijk volume. Daarna wordt
het bij gelijkblijvende temperatuur tot zijn oorspronkelijk volume samengeperst.
Tenslotte wordt het bij constant volume op zijn oorspronkelijke druk teruggebracht.
- Teken een p(V) en een p(T)-diagram van dit kringproces
- Bij welke temperatuur vond het samenpersen plaats?
- Wat is de hoogste druk geweest tijdens dit proces?
- Hoeveel mol gas werd er gebruikt?
- Duid op de grafieken de isobaar, de
isotherm en de isochoor aan.
5.5 Een hoeveelheid als ideaal te
beschouwen helium gas ondergaat de
toestandverandering beschreven in de
grafiek. In de toestand C bedraagt het
volume 100,0 l gas.
Bereken 1) het gasvolume in toestand A
Evaluatie druk p.40
2) het aantal mol gas
3) het normvolume van het gas
4) het aantal gasmoleculen
5) de massa gas
MH = 4 g/mol Vn = 22,4 l/ mol
NA = 6,022.1023 /mol
5.6 In de bodem van een sterk verontreinigd meer produceren micro-organismen
CH4-gasbelletjes die van de bodem opstijgen. Het meer is 20 m diep en de
massadichtheid van het water bedraagt 1013 kg/m³. Als een gasbelletje op de
bodem een volume heeft van 3,0 ml, hoe groot is dan het volume aan het
wateroppervlak? De temperatuur stijgt bij het stijgen van 4,1 °C op de bodem tot 15,2
°C aan de oppervlakte.
5.7 Een hoeveelheid dizuurstof (molaire massa 32 g/mol) zit bij een temperatuur van
25 °C en een druk van 3000 hPa in een stalen fles met een constant volume van 2,0
liter.
a. De fles wordt in de zon gelegd. Het gas warmt op tot 50 °C. Welke druk oefent het
gas dan uit?
b. Hoeveel gram gas zit er in de fles?
5.8 Een hoeveelheid gas is afgesloten en heeft een temperatuur van 17° C. Tot op
welke temperatuur moet men het gas verwarmen om de druk met 20° C te doen
toenemen, als het volume constant blijft?
5.9 Een autoband heeft bij een temperatuur van 12° C een druk van 3,4.105 bar.
Bereken de druk als de temperatuur van de band oploopt tot 50° C.
5.10 Bepaal het volume van een bepaalde massa gas bij 67 °C als het volume bij 37
°C 100 m³ bedraagt, als tijdens de toestandsverandering de druk constant blijft.
5.11 10,0 dm³ lucht op 27 °C en 101,3.10³ Pa worden tot op 127 °C verwarmd en
samengeperst tot 3,55.105 Pa . Bereken het nieuwe volume.
5.12 Bereken het volume van een hoeveelheid gas waarvan het normvolume 15,0
dm3 bedraagt, als men dit gas opwarmt tot 250°C en de druk oploopt tot 0,36 MPa.
5.13 Een bepaalde hoeveelheid gas wordt bij constant volume van 65°C afgekoeld
tot 0°C. De druk neemt af met 20 kPa. Bereken de begin- en einddruk.
Evaluatie druk p.41
6 Inzicht
6.1 Een gas zit opgesloten in een kolf die verbonden is met een U-buis gevuld met
water. De atmosferische druk bedraagt 1016 hPa. Bereken de druk die het gas in de
kolf uitoefent.
Wat zou je zien gebeuren als je de kolf met je handen zou verwarmen? Welke
toestandsfactoren van het gas veranderen er dan?
4,5 cm
6.2 Een zekere hoeveelheid gas zet uit bij constante temperatuur. Welke fysische
kenmerken van het gas stijgen van de hieronder vermelde?
a. Het gemiddeld aantal moleculen per volume.
b. De gemiddelde snelheid.
c. De gemiddelde kinetische energie.
d. De gemiddelde afstand tussen de moleculen.
e. Het gemiddeld aantal botsingen per tijd op de wand van het vat.
Verklaar elk antwoord met woorden en formules.
6.3 Tot welke temperatuur (in °C) moet men lucht van 10 °C verwarmen bij een
constant volume, opdat de druk zou verdubbelen?
6.4 Leid uit de algemene of ideale gaswet de volumewet van Gay-Lussac af voor
een isobaar proces.
6.5 Vul in met <, > of =
p a … pb
Evaluatie druk p.42
V a … Vb
Ta … Tb
6.6 Op welke wet steunt de werking van een fietspomp? Leg uit. Blijft de wet de
ganse tijd geldig? Verklaar.
6.7 Een hoeveelheid gas in de normomstandigheden ondergaat eerst een isotherm proces en dan
een isobaar proces. Toon aan, met een passende grafiek, dat het in bepaalde gevallen mogelijk is om
de normtoestand opnieuw te bekomen, alleen door een isochoor proces toe te passen.
Evaluatie druk p.43
7 Doevragen
7.1 Bij constante temperatuur werd de druk en het volume van een bepaalde
hoeveelheid gas gemeten.
Volgende resultaten werden gemeten:
volume V(ml)
50,0
16,7
10,0
7,14
5,56
4,55
druk p (kPa)
10
30
50
70
90
110
Construeer de grafieken: p(V) en p(1/V)
Welk evenredig verband bestaat er tussen de grootheden?
Stel de vergelijking van de p(V) grafiek op.
7.2 Uit te voeren proef
figuur 12
De atmosferische druk is 1013 hPa. In de buis rust een kwik draad op de lucht. De
lengte van de kwikdraad is 7,6 cm, de lengte van de lucht is 16,8 cm. Bereken de
druk van de opgesloten lucht. De buis wordt dan met het open einde naar beneden
gehouden. De lucht in de buis neemt nu een lengte in van 20,5 cm. Toon door
berekening aan dat de wet van Boyle geldig is.
Evaluatie druk p.44
WARMTE EN FASEOVERGANGEN
1 Meerkeuze
1.1 De metingen, voorgesteld op het rooster tonen de gebeurtenissen die zich
voordoen als men een kokende vloeistof laat afkoelen.
het gedeelte B toont:
A. het smelten
B. het stollen
C. het koken
D. het afkoelen van de vloeistof
E. het afkoelen van de vaste stof
1.2 In van A en vat B zijn de vaste stoffen smeltend. We verhogen voor beiden de
druk bij constante temperatuur
A. de stof wordt in beide vaten vloeibaar
B. de stof in A wordt vast, in B vloeibaar
C. de stof in A wordt vloeibaar, in B vast
D. er gebeurt niets
1.3 Tijdens de faseovergang van water naar ijs:
A. zal de temperatuur dalen.
B. zal er een volumevermeerdering optreden.
C. zal de dichtheid toenemen.
D. zal de kinetische energie van de moleculen dalen.
1.4 Vat 1 bevat verzadigde etherdamp (pmax = 58,70.10³ pa) bij 20 °C.
Vat 2 bevat onverzadigde etherdamp bij 20 °C.
Vat 3 bevat verzadigde waterdamp (pmax = 2,34.10³ Pa) bij 20 °C. Welk vat moet bij
deze temperatuur de sterkste wand bezitten?
Evaluatie druk p.45
A.
B.
C.
D.
vat 1
vat 2
vat 3
zowel vat 1 als vat 2
1.5 De damp in elk vat wordt samengedrukt bij een constante temperatuur tot het
volume een derde van het oorspronkelijke volume bereikt heeft. De damp in vat 2 is
na het samendrukken nog steeds onverzadigd. Als p1, p2 en p3 de respectievelijke
druk is in vat 1, vat 2 en vat 3, dan:
A. zijn p1, p2 en p3 verdrievoudigd
B. zijn p1 en p3 gestegen en is p2 verdrievoudigd
C. zijn p1 en p3 constant gebleven en is p2 verdrievoudigd
D. kun je niet weten
1.6 In een vat zit water van 110 °C. Het water kookt niet. De luchtdruk buiten het vat
bedraagt 1013 hPa. De druk in het vat is:
A. hoger dan de luchtdruk buiten het vat
B. gelijk aan de luchtdruk buiten het vat
C. kleiner dan de luchtdruk buiten het vat
D. kun je niet weten
1.7 Als je een ijsblokje in je drankje doet, wordt het koel omdat
A. het smelten van het ijsblokje koude afgeeft aan het drankje
B. het smelten van het ijsblokje warmte onttrekt aan het drankje
C. het verdampen van het drankje afgeremd wordt door de koude die het
ijsblokje afgeeft.
1.8 Je krijgt volgende gegevens:
freon (smelttemperatuur –158°C,kooktemperatuur –30°C)
benzeen (smelttemperatuur 5,50°C,kooktemperatuur 80,1°C)
In welke aggregatietoestand komen freon en benzeen voor bij 84°C ?
A. beiden gasvormig
B. beiden vloeibaar
C. freon gasvormig en benzeen vloeibaar
D. freon vloeibaar en benzeen gasvormig
1.9 Welke factor bevordert de vrije verdamping niet?
A. temperatuur
B. grootte van het vloeistofoppervlak
C. hoge luchtvochtigheid
D. luchtstroming boven de vloeisof
1.10 In een wasmachine gaat 10 kg water. Dit water moet opgewarmd worden van
15° C tot 85° C. Er gaat geen warmte verloren. Hoeveel warmte is daarvoor nodig?
A. 4,2 MJ
B. 0,7 MJ
C. 2,9 MJ
D. 3,6 MJ
Evaluatie druk p.46
1.11 Volgende grafiek heeft betrekking op water. Welke uitspraak is juist:
1
T
2
A.
B.
C.
D.
m1 < m2
m1 > m2
m1 = m 2
geen enkel van de vorige antwoorden
∆Q
1.12 Wat is de correcte definitie voor de specifieke warmtecapaciteit van een
voorwerp?
A. de hoeveelheid energie die nodig is om een voorwerp 1°C in temperatuur te
doen stijgen
B. de hoeveelheid energie die nodig is om 1 kg van dit voorwerp een
temperatuursverandering van 1°C te doen ondergaan
C. de hoeveelheid energie die nodig is om 1 kg water 1°C in temperatuur te doen
stijgen
D. de temperatuurstijging die nodig is om 1 kg van deze stof 1°C in temperatuur
te laten veranderen
1.13 Een lage temperatuur in een koelkast wordt verkregen door:
A. een gas te laten condenseren
B. een gas vast te laten worden
C. een vloeistof te laten stollen
D. een vloeistof te laten verdampen
Evaluatie druk p.47
2 Juist of fout
2.1 Van twee lichamen van dezelfde stof en dezelfde temperatuur heeft het lichaam
met de grootste massa de grootste inwendige energie en ook de grootste
warmtecapaciteit.
2.2 Een vloeistof kookt bij die temperatuur waarbij haar maximum dampdruk (minstens) gelijk is aan
de uitwendige druk op de vloeistof. Naarmate de uitwendige druk groter wordt, daalt de
kooktemperatuur.
2.3 Niet alle moleculen van een vloeistof hebben dezelfde snelheid. Het zijn de snelst bewegende
moleculen die bij verdamping uit de vloeistof ontsnappen. Daardoor vermindert de gemiddelde
snelheid van de vloeistofmoleculen, waardoor bij verdamping de temperatuur van de vloeistof daalt.
2.4 Twee even grote kubusvormige blokjes bezitten dezelfde massa maar het ene
blokje is vervaardigd uit goud en het andere uit zilver. Ze worden beiden verwarmd
tot op een temperatuur van 100 °C. Men legt de blokjes op een dik stuk paraffine.
Het smeltpunt van paraffine is 52 °C, de smeltingswarmte van paraffine is 147.10³
J/kg, van goud 67.10³ J/kg en van zilver 88.10³ J/kg. De warmtecapaciteit van
paraffine is 2900 J/kg.K, van goud 130 J/kg.K en van zilver 234 J/kg.K.
Het gouden blokje zakt dieper weg in de paraffine dan het zilveren blokje.
2.5 Er wordt thee geschonken uit de theepot.
Jan krijgt een klein kopje thee, moeder een grote beker vol thee. Onmiddellijk na het
uitschenken kan men dan zeggen:
- dat beide hoeveelheden thee dezelfde temperatuur hebben.
- dat beide hoeveelheden thee dezelfde warmte kunnen afstaan.
2.6 Een gas bezit geen inwendige potentiële energie.
2.7 Als in een gesloten vat damp voorkomt, is deze steeds verzadigd.
2.8 De damp die bij het koken in een vloeistof ontstaat onder de vorm van
dampbellen die naar het oppervlak stijgen, is verzadigd.
2.9 De proef van Tyndall toont aan dat een drukverhoging altijd een
smeltpuntverlaging veroorzaakt.
2.10 IJs smelt bij een temperatuur van 0,0 °C.
2.11 Gedurende het koken blijft bij toenemende druk de kooktemperatuur van een
zuivere stof constant.
2.12 De dampspanningslijn van een stof ligt des te hoger, naarmate de stof minder
vluchtig is.
2.13 “Als je aan een stof warmte toevoegt, stijgt de temperatuur altijd.”
2.14 In de vaste fase is de totale inwendige energie van een stof groter dan in de
vloeibare fase.
Evaluatie druk p.48
2.15 De inwendige energie van een gas bestaat hoofdzakelijk uit kinetische energie.
2.16 Bij het verdampen staat een stof warmte af.
2.17 Als de druk lager is dan de normaaldruk zal een stof bij een lagere temperatuur
koken dan bij de normaaldruk.
2.18 Een verzadigde damp voldoet aan de gaswetten.
2.19 Water wordt veelal als koelvloeistof gebruikt omdat het een laag kookpunt
heeft.
2.20 Een bekertje lauw water wordt onder de vacuümpomp geplaatst. De lucht wordt
weggezogen. Het water begint te koken op een lagere temperatuur.
2.21 Tijdens het koken blijft de temperatuur constant omdat de dampbellen de
aangevoerde energie afvoeren.
2.22 Van vaste stoffen A en B verwarmt men 1,5 kg op identieke elektrische
kookplaten met zelfde vermogen. De grafiek geeft het temperatuurverloop in functie
van de verwarmingstijd
Welke uitspraken zijn juist of vals en waarom?
L: latente smeltingsarbeid (smeltingswarmte)
c: specifieke warmtecapaciteit in vaste toestand
a L A = 2 x LB.
b LB = 2 x LA
c LA = LB
d cA = 2 x cB
e cA = cB
f cB = 2 x cA
Evaluatie druk p.49
3 Reproductie
3.1 Gegeven: p(V)-diagram van een stof; kritische isotherm.
Gevraagd: 1) Teken vanaf punt A wat er gebeurt indien je bij een constante
temperatuur het volume laat toenemen.
2) Teken vanaf punt B wat er gebeurt indien je bij een constante temperatuur de druk
verlaagt.
3.2 Water is aan het koken. Welke stof is er aanwezig in de bellen die we naar de
oppervlakte zien stijgen? Hoe groot is de druk binnen deze bellen?
3.3 Een damp is onverzadigd en wordt isotherm samengedrukt tot er verzadiging is
en er ook wat condensatie optreedt.
a) Beschrijf en teken de opstelling die hiervoor gebruikt kan worden.
b) Stel het proces voor in een p(V)-diagram
c) Stel het proces voor in een p(T)-diagram
3.4 In een ijzeren ketel bevindt zich 1 liter water van 20 °C. Hoe kan je de inwendige
energie van het water verhogen? Verklaar!
3.5 Waarom kan water in een volledig afgesloten vat niet aan de kook gebracht
worden?
3.6 Een faseovergang gaat steeds gepaard met een verandering van de inwendige
energie van de stof. Verklaar! Hoe noemt men de toegevoerde warmte in dit geval.
3.7 Bij paraffine zal een drukverhoging het smeltpunt verhogen. Verklaar aan de
hand van het deeltjesmodel.
3.8 Leg uit waarom een verzadigde damp niet voldoet aan de wet van Regnault.
3.9 Leg de volgende begrippen uit (geef, waar mogelijk, een tekening)
Evaluatie druk p.50
a. Beginsel van Watt
b. Proef van Tyndall
c. Kritisch punt
3.11 In een cilinder met zuiger is er vloeistof en damp aanwezig.
Welk soort damp heeft men? (verzadigd of onverzadigd)
Wat weet je over het verdampingsproces op dat moment? (energiebeschouwingen)
Wat gebeurt er als je de zuiger verplaatst bij constante temperatuur?
Wat gebeurt er als je de temperatuur verhoogt zonder de zuiger te verplaatsen?
3.12 Wat stellen we vast betreffende het oppervlak als we gesmolten paraffine laten
stollen? Leg uit.
3.13 Noem 2 soorten vloeistofthermometers en schrijf achter elke pijl of ze gebruikt
worden voor het meten van lage of hoge temperaturen.
→
→
3.14 Vergelijk de eigenschappen van een reëel gas met deze van een ideaal gas.
3.15 Leid de algemene gaswet af.
3.16 “Een calorimeter heeft een warmtecapaciteit van 100 J/K”. Wat wil men
hiermee zeggen?
Evaluatie druk p.51
4 Grafieken
4.1 Men neemt een hoeveelheid ijs met een temperatuur van -40 °C. Men gaat die
verwarmen en men leest om de 5 minuten de temperatuur af.
Tijd (in
minuten)
0
5
10
15
20
25
30
35
40
Temperatuur
(in °C)
Tijd (in
minuten)
-10
-5
0
0
0
0
10
20
30
45
50
55
60
65
70
75
80
85
40
50
60
70
80
90
100
100
100
Temperatuur
(in °C)
Zet de meetresultaten in een (temperatuur)-tijd diagram.
Duid verzorgd en heel nauwkeurig met behulp van een gekleurde lijn (geen rood) op
bovenstaande grafiek aan waar je "enkel" ijs, water en waterdamp aantreft.
Wat betekenen de horizontale stukken op de grafiek? (Geef weer in juiste volgorde)
Waarom stijgt de temperatuur (voorlopig) niet boven 100°C en waarvoor dient de
toegevoegde energie?
4.2 Teken het p(T)-diagram voor de stof water en duidt de volgende processen aan:
1) smeltend ijs in een glas water.
2) waterdamp die condenseert tegen de ruiten.
3) rijmvorming op een zomermorgen
4) isotherm sublimeren van ijs.
4.3 Deze grafiek is de grafische voorstelling van het smeltproces van een stof.
a) Hoe groot is de smelttemperatuur?
b) Welke toestand heeft de grootste soortelijke warmtecapaciteit?
q (°C)
120
100
80
60
40
20
0
0
10
20
30
40
50
60
70
80
tijd (min)
Evaluatie druk p.52
4.3 Gegeven het toestandsdiagram van een stof. Elk punt van de grafiek geeft een
toestand van de stof aan.
In welke aggregatietoestand komt deze stof voor voorgesteld door het punt:
- a?
- b?
- c?
- d?
Wat is de naam van het punt t? In welke aggregatietoestand(en) bevindt de stof zich
in dit punt?
Beschrijf de aggregatietoestanden en de faseovergangen die deze stof doorloopt,
vertrekkend vanuit het punt b, als de druk isotherm verlaagt tot hij even groot is als
de druk pc (de druk in toestand c).
Beschrijf de aggregatietoestanden en de faseovergangen die deze stof doorloopt,
vertrekkend vanuit het punt a, als de temperatuur isobaar verhoogt tot hij even groot
is als de temperatuur Td (de temperatuur in toestand d).
Van de stof is gekend dat ze sublimeert in normtoestand. Zet op de assen van de
grafiek de normwaarden uit. (slechts één oplossing geven)
4.4 In een gesloten fles bevindt zich ether in vloeibare en in dampfase
a. Is de damp verzadigd? Leg uit.
b. Als de fles in de zon gezet wordt stijgt de temperatuur. Teken een grafiek die de
druk in functie van de temperatuur voorstelt (veronderstel dat het volume van de fles
constant blijft).
c. Verklaar het verloop van de grafiek.
4.5 Men verwarmt gelijke massa's van 2 vaste stoffen A en B op elektrische
kookplaten die een zelfde vermogen leveren. Op de grafiek hieronder wordt de
temperatuur als functie van de tijd voorgesteld. Schrap in de volgende uitspraken de
foute antwoorden.
Evaluatie druk p.53
a. De specifieke warmtecapaciteit van vaste stof A is groter dan / kleiner dan / gelijk
aan de specifieke warmtecapaciteit van vaste stof B.
b. De smelttemperatuur van stof A is hoger / lager / gelijk aan de smelttemperatuur
van stof B.
c. De specifieke smeltingswarmte van stof A is groter dan / kleiner dan / gelijk aan de
specifieke smeltingswarmte van stof B.
4.6 IJs komt uit de koelkast. Het wordt langdurig verwarmd tot het kookproces wordt
bereikt. Bespreek de zones A, B, C en D. Definieer de begrippen met betrekking op
de faseovergangen. Duid op de grafiek de ontbrekende symbolen aan.
4.7 De stof in punt A ondergaat een afkoeling bij een constante druk. Welke
verschillende toestanden worden doorlopen?
Stel de overgang BCD voor in een p(V)-grafiek en geef de nodige uitleg.
p
D
°
°
C
°
A
°
B
T
Evaluatie druk p.54
4.8 Een blok ijs van –20 °C wordt gelijkmatig verwarmd. De meetresultaten zijn
uitgezet in een grafiek.
grafiek 13
Vul aan:
in de beker zit na 2 minuten: ...
na 4 minuten: ...
na 6 minuten: ...
Hoe noemen we het punt a? ...
Hoe noemen we het punt b? ...
Wat gebeurt er met de temperatuur na het punt b? ...
Evaluatie druk p.55
5 Rekenvragen
5.1 Een thermos met warmtecapaciteit 80 J/K bevat 300 g water op 8,0 °C. Je wilt
de temperatuur er van doen dalen tot 2,0°C. Hoeveel g ijs op -8,0°C moet je
toevoegen?
(Ls ijs = 335.103 J/kg; cijs = 22.102 J/kg.K)
5.2 a)Een calorimeter met verwarmingsspiraal bevat 300,0 ml olijfolie bij 15,0 °C.
Brengt men hierbij 700,0 g loodkorrels van 100,0 °C dan stijgt de temperatuur tot
25,0 °C.
Bereken hieruit de warmtecapaciteit van de calorimeter.
b) We sturen door het geheel gedurende 5 minuten (gemeten tot op 1 seconde
nauwkeurig) elektrische stroom. De spiraal heeft een vermogen van 50,0 W.
Met hoeveel graden Celsius stijgt de temperatuur?
Enkele waarden: colijfolie = 1970 J/kg K
clood=129 J/kg K
ρolie=918 kg/m3
5.3 In een calorimeter met warmtecapaciteit 120 J/K die 250,0 g water van 5,0 °C
bevat, brengt men 750,0 g ijs. Bij thermisch evenwicht is er 28,0 g ijs meer aanwezig.
Bepaal de begintemperatuur van het ijs.
5.4 Een glas met warmtecapaciteit 60 J/kg bevat 240 g limonade op 16,3 °C. Je wil
de limonade afkoelen tot 7,0 °C. Hoeveel gram ijs van -25,5 °C moet je toevoegen?
Voor limonade kan je de soortelijke warmtecapaciteit van water gebruiken.
5.5 In een calorimeter met warmtecapaciteit 105 J/K die 640 g water bij 20 °C bevat,
brengen we 100 g smeltend ijs. De eindtemperatuur van het stelsel wordt 7 °C.
Bereken hieruit de specifieke smeltingswarmte van ijs.
5.6 Hoeveel kg steenkool zijn er nodig om 150 kg ijs van –10,0 °C om te zetten in
damp van 100,0 °C? (Verbrandingswarmte van steenkool: 335.105 J/kg, rendement =
60 %)
5.7 Twee bollen A en B zijn uit hetzelfde materiaal vervaardigd. De straal van bol A is dubbel zo groot als
de straal van bol B. Als A en B een zelfde warmtehoeveelheid opnemen en de temperatuur van B
hierdoor stijgt met 40 K, welke temperatuurverandering ondergaat bol A dan?
5.8 Op een rustige zomerdag kom ik thuis met een fles cola in de boodschappentas.
De kinderen komen bijna om van de dorst en vragen om een fris glas cola. Op de
fles staat vermeld dat de cola het lekkerst smaakt bij 7,0° C. Met een
omgevingstemperatuur van 24° C niet direct een simpele opgave!
Daarom neem ik een glas met C = 120 J/K, vul het met exact 125 g cola en voeg er
een ijsblokje van 12,2 g met een temperatuur van – 18° C aan toe. Kunnen de
kinderen een “lekkere” cola drinken of niet in de veronderstelling dat er geen
warmteverlies op de omgeving is? Bereken!
Evaluatie druk p.56
5.9 In een kraamkliniek mengt een verpleegster 8,00 kg water van 32,0° C met 8,00
kg water van 42,0° C in een inox wastafel met C = 12600 J/K. cw = 4186 J/kgK.
Waarom bekomt er geen eindtemperatuur van 37,0° C om de baby in te wassen?
Welke redeneerfout maakt zij?
Bereken de exacte eindtemperatuur.
5.10 In een bad met C = 16075 J/K bevindt zich 41,5 kg water van 27,8° C. Hoeveel
water van 55,0° C moet men toevoegen om water van 40,0° C te bekomen? cw =
4186 J/kgK
5.11 Een blok aluminium van 2,5 kg wordt in een oven opgewarmd en nadien in een
calorimeter gebracht die 5 kg olie van 20,0°C bevat. Bij evenwicht is de temperatuur
34,7°C Bereken de oventemperatuur. (colie = 2500 J/kg.K en cAl = 130 J/kg.K) Heeft
de warmtecapaciteit van de calorimeter (Ccal = 250 J/K) een invloed op het resultaat
?
5.12 Een koperen calorimeter heeft een massa van 500 gram. Hij bevat 400 g water
op 2°c. Men gooit er een blokje ijs in van 20 g met een temperatuur van – 2 °C. Men
leidt er ook waterdamp in van 110 °C. De eindtemperatuur bedraagt 20 °C. Bereken
de massa van de gecondenseerde waterdamp.
CCu = 3,86.10² J/kg.K ; cijs = 22.10² J/kg.K ; ls(ijs) = 335.10³ J/kg ; cw = 4186 J/kg.K ;
lv(water) = 2270.10³ J/kg ; cwd = 2020.10² J/kg.K.
5.13 In een calorimeter met warmtecapaciteit 84,0 J/kg die 500 g alcohol op 7,9 °C
bevat, brengt men 925 g ijzer op 100,0 °C. De evenwichtstemperatuur wordt 29,5 °C.
Bereken hieruit de soortelijke warmtecapaciteit van alcohol.
5.14 Een spoorstaaf heeft bij 0 °C een lengte van 30 m. Hoeveel is die staaf langer
geworden bij 35 °C. De lineaire uitzettingscoëfficiënt van ijzer is 12 .10-6 1/°C .
5.15 Een thermos met warmtecapaciteit C = 104,8 J/K bevat 200 g water op 14,0 °C.
Een stuk metaal van 400g dat een temperatuur van 84,5 °C heeft wordt in de
thermos gebracht. De soortelijke warmtecapaciteit van het metaal bedraagt 1340
J/kg.K. Bereken de eindtemperatuur.
Evaluatie druk p.57
6 Inzicht
6.1 Verklaar waarom brandwonden, veroorzaakt door hete waterdamp, steeds veel
erger zijn dan de brandwonden van kokend water.
6.2 Het basiskamp voor de beklimming van de Mount Everest ligt op een hoogte van
5000 m. De luchtdruk is daar ongeveer 550 hPa. Waarom is het zinloos ether mee te
nemen om eventueel medisch materiaal te reinigen?
6.3 Waarom wordt precies water gebruikt als koelvloeistof voor de motor van een
wagen?
6.4 Waarom verandert onze lichaamstemperatuur nauwelijks als we vanuit de
vrieskou in een warme sauna stappen.
6.5 Geef twee redenen waarom je hand niet bruikbaar is als thermometer.
6.6 Aan één kilogram van elk van de metalen in de tabel wordt in dezelfde tijd,
evenveel warmte toegevoegd. Er gaat geen warmte verloren. De begintemperatuur
van de metalen is gelijk. Welk metaal bereikt de hoogste temperatuur? Bewijs.
Metaal
Aluminium
Goud
Koper
Zilver
C J/kgK
904
130
386
234
6.7 In een calorimeter met 100 g water, brengen we 200 g ijs. Na de nodige tijd te
wachten om thermisch evenwicht te bereiken, vinden we nog altijd 100 g water en
200 g ijs. Hoe kan dit?
6.8 In een calorimeter met 100 g water, brengen we 200 g ijs. Na de nodige tijd te
wachten om thermisch evenwicht te bereiken, vinden we 120 g water en 180 g ijs.
Wat is de eindtemperatuur? Waarom?
6.9 Verklaar aan de hand van de specifieke warmtecapaciteit en de maximum
dampdruk waarom kwik een goede thermometervloeistof is.
6.10 Waarom worden aardappelen vlugger gaar in een kookpan met deksel, dan in
een kookpan zonder deksel?
6.11 Waarom is zweten een natuurlijke bescherming tegen de warmte?
6.12 Men kan melk beter fris houden door de fles te wikkelen in natte doeken dan
door de fles onder te dompelen in een emmer water. Verklaar.
6.13 Een blokje ijs van 0° C wordt in een beker verwarmd boven een
bunsenbrander. Men stopt de verwarming als het ijs is omgezet naar water van 0° C.
Evaluatie druk p.58
6.14 Heeft de verwarming invloed op de EP van de deeltjes? Ja of nee? Leg uit.
Heeft de verwarming invloed op de EK van de deeltjes? Ja of nee? Leg uit. Is de
inwendige energie van deze stof groter of kleiner geworden? Zeg waarom.
6.15 In welke aggregatietoestand of fase komt de stof voor bij een normale druk en
de opgegeven temperatuur?
stof
smeltpunt (°C) kookpunt (°C) temperatuur (°C)
ijzer
1535
-
1700
Keukenzout
808
-
750
alcohol
-114
78
-80
stikstof
-210
-196
-150
6.16 Waarom is de kooklijn van water geen rechte?
6.17 Als we een vochtige doek bij vorst buiten hangen is hij na een tijdje stijf
bevroren. Na een lange tijd wordt hij terug zacht en droog. Verklaar.
6.18 Bij vriesweer na regen ontstaan scheuren in de rotsen.
6.19 Een vliegtuig dat op grote hoogte passeert trekt een wit-grijs spoor in de lucht,
een laagvliegend vliegtuig doet dat niet.
6.20 Een kok bij een Himalaya expeditie heeft meer geduld nodig dan zijn collega in
een restaurant in Gent.
6.21 Als je op een warme zomerdag in het koele water van een zwembad duikt, krijg
je het een paar ogenblikken koud. Kom je na enkele tijd uit het koele water in de
warme lucht, dan krijg je het opnieuw koud. Verklaar.
6.22 Schets het toestandsdiagram van water. Benoem de verschillende lijnen en
bepaal daaruit de aggregatietoestand.
Benoem en bespreek het tripelpunt en het kritisch punt.
Waarin verschilt dit diagram van het diagram van andere stoffen? Verklaar.
Evaluatie druk p.59
7 Doevragen
7.1 In een calorimeter bevindt zich een massa water in evenwicht met een massa
ijs. Bij welke temperatuur is het stelsel? Waarom?
In het geheel is er een elektrische dompelaar met vermogen 300 Watt en een
thermometer gebracht. Om de 30 seconden wordt de temperatuur afgelezen van het
stelsel.
Men meet volgende resultaten:
Tijd in seconde
0
30
60
90
120
150
180
210
240
270
Temperatuur in °C
0
0
0
0
0
9,6
19,2
28,8
38,4
48,2
Bereken de massa ijs en de massa water die oorspronkelijk aanwezig waren. Zet het
proces uit in een T(Q)-diagram en een Q(T)-diagram
7.2 Giet een weinig alcohol op je hand. Het voelt koud aan. Verklaar.