De natuurkunde van supergeleiding

De natuurkunde van
supergeleiding
1. Inleiding / Verschijnselen
Het begin van de ontdekking van supergeleiding werd gemarkeerd door een discussie
over de temperatuurafhankelijkheid van de weerstand van metalen. Volgens de
klassieke theorie (P. Drude en H.A. Lorentz) waren er twee mogelijkheden voor het
limietgeval van het absolute nulpunt:


Elektronen zullen op de atomen gaan condenseren; het metaal zal een isolator
worden bij T = 0 K.
Er is geen condensatie; de weerstand gaat naar nul als de wortel van T.
Echter, experimenten onthulden dat geen van deze twee verwachtingen bewaarheid werd.
Nadat Heike Kamerlingh Onnes in 1908 succes had geboekt met het vloeibaar maken van
helium (bij 4.2 K), kon gemeten worden bij zeer lage temperaturen met als resultaat dat
de weerstand van metalen naderde tot een eindige waarde die sterk afhankelijk bleek van
onzuiverheden in het metaal. Voor zeer zuivere monsters zou de weerstand daarom naar
nul gaan, omdat de waargenomen temperatuurafhankelijkheid in verband gebracht kon
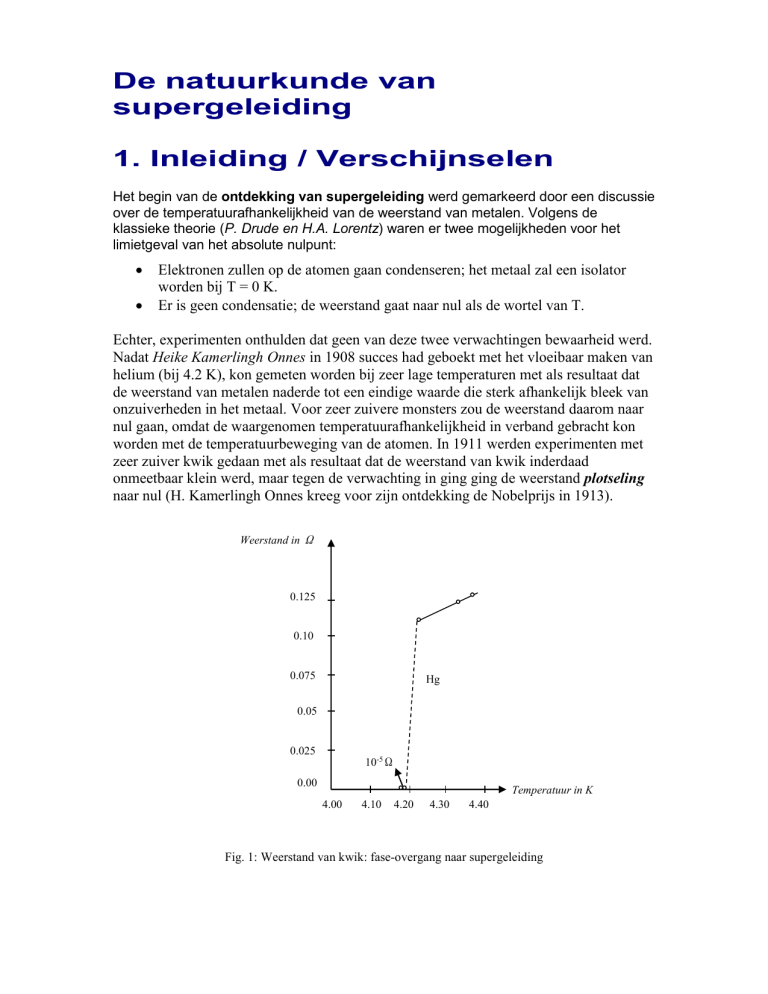
worden met de temperatuurbeweging van de atomen. In 1911 werden experimenten met
zeer zuiver kwik gedaan met als resultaat dat de weerstand van kwik inderdaad
onmeetbaar klein werd, maar tegen de verwachting in ging ging de weerstand plotseling
naar nul (H. Kamerlingh Onnes kreeg voor zijn ontdekking de Nobelprijs in 1913).
Weerstand in Ω
0.125
0.10
0.075
Hg
0.05
0.025
10-5Ω
0.00
Temperatuur in K
4.00
4.10
4.20
4.30
4.40
Fig. 1: Weerstand van kwik: fase-overgang naar supergeleiding
Kort daarna werd ontdekt dat de weerstand boven een kritische stroomdichtheid weer
eindig werd.
Een ander verschijnsel van supergeleiding is van magnetische aard – het zogenaamde
"Meissner-Ochsenfeld Effect": supergeleiders vertonen de eigenschap dat zij het
aangelegde magneetveld volledig verdrijven, onafhankelijk of het veld vóór of na de
overgang naar supergeleiding is aangelegd.
Fig. 2: Meissner-Ochsenfeld-Effect
http://commons.wikimedia.org/wiki/Image:EfektMeisnera.svg
Een supergeleider gedraagt zich dus als perfect diamagnetisch materiaal. Er bestaat echter
een kritische magnetische veldsterkte waarboven de supergeleiding ineenstort. In feite
is het juist dit magnetische gedrag dat een materiaal bewijsbaar tot een supergeleider
maakt.
Een fundamentele theoretische beschrijving kwam echter niet van de grond tot 1957, toen
J. Bardeen, L.N. Cooper en J.R. Schrieffer erin slaagden een consistente quantumtheorie
voor supergeleiding te ontwikkelen (BCS-theorie). Een macroscopisch zichtbaar gevolg
van de quantumnatuur van supergeleiding is het Josephson effect dat leidde tot de
onwikkeling van vele nieuwe technische toepassingen.
Het hierboven beschreven magneetgedrag is kenmerkend voor zogenaamde Type I
Supergeleiders, in de meeste gevallen metaalelementen. Later werd een andere soort
supergeleider gevonden genaamd Type II Supergeleiders, vooral legeringen en
chemische verbindingen. Zij vertonen twee kritische magnetische veldsterktes: onder de
eerste veldsterkte is het materiaal in de Meissner toestand (zoals een Type I
Supergeleider), tussen de eerste en de tweede veldsterkte is het in een zogenaamde
gemengde of Shubnikov toestand, en boven de tweede kritische veldsterkte wordt het
materiaal weer een gewone geleider. De tussenfase wordt gekarakteriseerd door de
verschijning van flux wervels in het materiaal, die elk een gequantiseerde eenheid van
magnetische flux ("fluxoïde") dragen. Als de wervels op hun plaats gehouden worden
door kristalfouten of onzuiverheden ("pinning"), kan het materiaal vrij hoge
magneetvelden verdragen en wordt dan een "Harde Supergeleider" genoemd. Zulke
materialen zijn daarom heel goed bruikbaar voor technische toepassingen.
Tussen 1986 en 1993 is een nieuw type supergeleider ontdekt: de zogenaamde "HogeTemperatuur (High-Tc) Supergeleiders". Zij worden gekenmerkt door zeer hoge
kritische temperaturen, waarvan sommige een redelijke marge boven het kookpunt van
vloeibare stikstof liggen (77 K). J.G. Bednorz en K.A. Müller kregen in 1987 de
Nobelprijs toegekend voor het openen van het nieuw onderzoeksterrein van deze
supergeleiders. Inmiddels ligt de record kritische temperatuur rond de 160 K.
De meeste materialen van deze soort zijn keramisch en de natuurkunde achter hun
supergeleiding is nog niet volledig begrepen.
2. Elektrische eigenschappen
Supergeleiding beschijft, zoals de uitdrukking al aangeeft, het verschijnsel dat een stuk
materiaal een perfecte geleider wordt met elektrische weerstand nul, en wel zeer
plotseling beneden een bepaalde temperatuur: de kritische temperatuur Tc. Normaal
gesproken vindt de overgang plaats bij zeer lage temperaturen net boven het absolute
nulpunt. Hoe terecht is het om hier te spreken van het verdwijnen van de weerstand? Ten
tijde van de ontdekking lag de meetnauwkeurigheid rond 10-5, vandaag de dag kan de
weerstandsdaling bij de overgang naar supergeleiding gemeten worden met een
nauwkeurigheid van 10-14. Dit kan men doen door te kijken naar de afname van een
stroom in een supergeleidende ring (Kammerlingh Onnes gebruikte deze zeer gevoelige
methode al in 1914): eerst wordt een staafmagneet in de een ring gestopt die in zijn
gewone toestand is, en daarna wordt de ring afgekoeld tot beneden de kritische
temperatuur van het materiaal. Als de magneet dan wordt weggehaald, wordt er in de ring
een stroom geïnduceerd. Als deze stroom afneemt met de tijd, is er beslist sprake van
weerstand van de geleider; indien niet, kan een bovengrens van de weerstand worden
bepaald.
Is
N
B
B
T > TC
T < TC
Fig. 3: Opwekking van een superstroom in een supergeleidende ring: eerst wordt de ring afgekoeld, dan
wordt de magneet weggehaald.
De lage weerstand van metalen is nauw verbonden met het feit dat het transport van
lading in het materiaal plaatsvindt door zogenaamde vrije elektronen. In feite zijn zij niet
helemaal vrij omdat de elektronen onderweg met elkaar botsen, wat aanleiding geeft tot
een zogenaamde intrinsieke bijdrage tot de weerstand (die bijna onafhankelijk van de
temperatuur is), én met de ionen van het kristalrooster botsen (wat eigenlijk elementaire
roosterexcitaties oplevert die men fononen noemt). De laatste bijdrage nu is sterk
temperatuurafhankelijk. Waarom zou in een supergeleidend materiaal de energie
uitwisseling tussen de geleidingselektronen en het rooster plotseling verboden zijn? Het
duurde bijna tot 1930 voordat het idee begon post te vatten dat supergeleiding een
macroscopisch quantum verschijnsel moest zijn. Vaste stoffen die onder normale
omstandigheden goede geleiders zijn (zoals koper, zilver, goud) worden vaak niet
supergeleidend, terwijl veel slechte geleiders wél supergeleiders kunnen worden. De
reden voor de laatste constatering ligt in de sterke elektron-fonon verstrooiing die bij
slechte geleiders een rol speelt en leidt tot een grote weerstand in de gewone toestand,
terwijl hetzelfde effect ook verantwoordelijk is voor het mechanisme van supergeleiding.
Ook het bestaan van de beperkte stroomdichtheid (kritische stroom) die een supergeleider
kan dragen is gekoppeld aan dit mechanisme (zie paragraaf 4).
3. Magnetisch gedrag
Supergeleiders gedragen zich in een magneetveld heel anders dan (zelfs perfecte) metaal
geleiders: een supergeleider is een perfect diamagnetisch materiaal, de geïnduceerde
magnetisatie compenseert het aangelegde magneetveld volledig – maar slechts tot aan
een kritische veldsterkte Bc (zie fig. 4a).
-4πM
B
Type 1
Bc
Meissner
Bc
Tc
B
a)
T
b)
Fig. 4: a) Geïnduceerde magnetisatie in een (Type I) supergeleider als functie van het aangelegde
magneetveld
b) Afhankelijkheid van de kritische magnetische veldsterkte van de temperatuur
In 1935 ontdekten W. Meissner en R. Ochsenfeld het effect (dat later naar ze genoemd
zou worden) dat een magnetische flux altijd uit het supergeleidende materiaal verdreven
wordt, onafhankelijk van het feit of het magneetveld aangelegd was vóór of na de
overgang naar supergeleiding. Het effect is dus onafhankelijk van zijn voorgeschiedenis
en is daardoor reversibel in de thermodynamische zin van het woord. Supergeleiding is
om die reden een echte thermodynamische toestand.
De afhankelijkheid van de kritische magnetische veldsterkte van de temperatuur kan zeer
goed benaderd worden met de eenvoudige uitdrukking (zie fig.4b)
Bc(T) = Bc(0) [1 – (T/Tc)²] .
Kort na de ontdekking van het Meissner-Ochsenfeld-Effect werd er een
fenomenologische theorie van de supergeleiding ontwikkeld door F. en H. London. Eén
van voorspellingen ervan was dat het magneetveld niet volledig tot aan het oppervlak van
de supergeleider uitgedreven wordt, maar dat het doordringt in een nauwe
oppervlakteschil waarbinnen de compensatiestromen lopen. De karakteristieke diepte van
deze laag heet de London doordringdiepte L, en is typisch in de order van 50 nm. Het
feit dat het gehele energietransport plaatsvindt binnen een nauwe oppervlaktelaag van een
supergeleidende draad kan gebruikt worden als praktische toepassing: duizenden dunne
supergeleidende draden opgesloten in een koper matrix kunnen stroom geleiden beneden
de kritische temperatuur. Zou om een of andere reden de supergeleiding echter
verdwijnen dan kan het kopermateriaal het stroomtransport overnemen en op die manier
zorgen dat de draad heel blijft.
Als men de Bohr-Sommerfeld quantisatie regel toepast op de stroom in een
supergeleidende ring (d.w.z., op een macroscopisch system!), krijgt men het resultaat dat
de magnetische flux gequantiseerd is, dus dat de magnetische flux bestaat uit elementaire
eenheden van "fluxoïden"
0 = h/2e0 = 2.07 x 10-15 Tm² (= Vs)
waarin h de constante van Planck is en e0 de elementaire eenheidslading. In feite komt in
de noemer de lading van de ladingsdragers voor die experimenteel is bepaald op twee
keer elementaire eenheidslading, wat aangeeft dat de elektronen in een supergeleider
voorkomen in paren (dit zal in meer detail worden uitgewerkt in de volgende paragraaf).
4. BCS-Theorie
De BCS-Theorie (waarvoor J. Bardeen, L.N. Cooper, en J.R. Schrieffer in 1972 de
Nobelprijs kregen toegekend) is een quantum-mechanische veeldeeltjestheorie om
supergeleiding in metalen te verklaren. De experimentele constatering dat de kritische
temperatuur sterk afhankelijk is van de verhouding lichte/zware isotopen in het metaal
("isotopie effect") was een aanwijzing dat massa-afhankelijke gequantiseerde
roostertrillingen (waarvan de quanta fononen worden genoemd) een wezenlijke rol spelen
in de vorming van een supergeleidende toestand. Ook de waarde van een energiesprong
gevonden bij metingen van de soortelijke warmte in het elektronische excitatie spectrum
van supergeleiders beneden Tc wees op de vorming van elektronparen in de
supergeleidende toestand.
De basisgedachte achter de BCS-Theorie berust op de vorming van zogenaamde Cooperparen bestaande uit twee elektronen (met tegengestelde impuls en spin, zie beneden).
Deze paarvorming kan worden gerealiseerd als men een nieuwe, licht aantrekkende
elektron-elektron wisselwerking veronderstelt, gebaseerd op de emissie en absorptie van
virtuele fononen. Een en ander kan worden geïnterpreteerd als volgt: de emissie van een
virtueel fonon door een elektron staat gelijk met een afbuiging van de plaatselijke
roosterionen en dus met de lokale polarisatie van het rooster. Als een ander elektron deze
polarisatiewolk betreedt, voelt het een aantrekkingskracht (door de absorptie van het
virtuele fonon), onafhankelijk van de Coulomb afstoting tussen de elektronen (het moet
hier worden opgemerkt dat de uitgewisselde fononen niet reëel kunnen zijn omdat een
reëel fonon aanleiding zou geven tot de overdracht van energie op het rooster, hetgeen
weer een niet-verdwijnende weerstand zou veroorzaken).
De resulterende vorming van Cooperparen is een dynamisch proces: het hangt af van de
snelheid waarmee het rooster de polariserende werking van de elektronen kan volgen, en
dus spelen de massa’s van de ionen een doorslaggevende rol. Dit verklaart het eerder
genoemde isotopie effect in de kritische temperatuur. Omdat het rooster veel trager
reageert dan de elektronen die erdoor bewegen, strekt de koppeling van het Cooperpaar
zich uit over afstanden van 100 nm tot 1000 nm; deze afstand wordt de "coherentie
lengte" genoemd en kan opgevat worden als de gemiddelde omvang van het Cooperpaar.
Binnen deze afstand bevinden zich 106 tot 107 andere elektronen, eveneens als
Cooperparen die continu vervallen en weer gevormd worden.
Een quantum-mechanische berekening toont aan dat alle Cooperparen een totale impuls
nul hebben (bij T = 0 K) en een tegengestelde spin. Daarom gedraagt elk Cooper paar
zich als een boson die bij voorkeur allemaal in dezelfde quantum-mechanische energie
toestand zitten. Ook wordt het geheel van alle paren beschreven door één enkele
golffunctie die de hele supergeleider bestrijkt. De bindingsenergie van een Cooperpaar is
in de orde van een paar meV, veel kleiner dan de bindingsenergie van elektronen in een
metaal (enkele eV), waardoor koppeling van elektronen in Cooperparen alleen mogelijk
is als de thermische energie van het rooster klein is. Deze bindingsenergie verklaart
uiteraard de hierboven genoemde energiesprong in het elektronspectrum.
Net beneden de kritische temperatuur condenseert maar een klein gedeelte van de
geleidingselektronen in Cooperparen; bij het dalen van de temperatuur worden er steeds
meer paren gevormd tot bij T = 0 K alles gekoppeld is.
Als er een elektrisch veld wordt aangelegd krijgen alle paren dezelfde impuls zonder
enige wisselwerking met het rooster, hetgeen aanleiding geeft het waargenomen
weerstandsvrije lading transport. De hoeveelheid impuls die op de paren kan worden
overgedragen is beperkt: op het moment dat de kinetische energie van de paren hun
bindingsenergie overtreft stort de supergeleiding ineen – dit is de reden voor het bestaan
van een kritische stroom. Ook magneetvelden kunnen alleen maar tot aan een bepaalde
veldsterkte toegepast worden, omdat de compensatiestroom anders de kritische waarde
zou bereiken.
Samenvattend kan men opmerken dat de BCS-Theorie slechts drie parameters nodig
heeft om de essentiële eigenschappen van supergeleiding in metalen uit te drukken: dat
zijn de kenmerken van het elektron deelsysteem (dichtheid van toestanden dichtbij het
Fermi oppervlak), van het rooster (karakteristieke fonon frequenties), en de sterkte van de
elektron-fonon koppeling.
5. De Josephson effecten
In het geval twee supergeleiders verbonden zijn met een dunne laag niet supergeleidend
materiaal (met een dikte van maar een paar nanometer) voorspelt de quantumtheorie een
eindige waarschijnlijkheid dat Cooperparen door de barrière (tunneljunctie) heen van de
ene supergeleider naar de andere kunnen tunnelen. Men zegt in dat geval dat de twee
supergeleiders zwak gekoppeld zijn. Zo’n combinatie heet een Josephson contact,
genoemd naar Brian D. Josephson die het verschijnsel in 1962 theoretisch voorspelde en
die, na experimentele verificatie van zijn voorspellingen, in 1973 de Nobelprijs kreeg
toegekend. Het Josephson contact kan een supergeleider-isolator-supergeleider (SIS) of
supergeleider-gewone geleider-supergeleider (SNS) combinatie zijn, gemaakt worden
door een dun supergeleidend punt op een andere supergeleider te drukken, dan wel door
een hele kleine samentrekking in een supergeleidende film.
US
S
S
I
R
U0
Fig. 5: Josephson contact
Het feit dat alle Cooperparen in een supergeleider in dezelfde quantum-mechanische
toestand zijn, houdt ook in dat de fase van de golffunctie van de paren goed bepaald is.
Als er een spanning U0 over het contact gezet wordt, zal er een weerstandsvrije
superstroom Is (Josephson stroom) door gaan ter grootte van
Is = Ic sin () .
Hierin is  het faseverschil tussen de golffuncties van de twee gekoppelde
supergeleiders, analoog aan het faseverschil tussen twee zwak gekoppelde mechanische
slingers. De waarde van Is kan verhoogd worden door de aangelegde spanning U0 te
verhogen tot aan de kritische stroom Ic. Dit verschijnsel heet het DC Josephson effect.
Als de stroom groter wordt dan Ic, zal er een spanning Us over de barrière (tunneljunctie)
ontstaan, d.w.z. er heeft zich dan een bepaalde weerstand ontwikkeld. Deze spanning
betekent een energieverschil tussen de Cooperpaar systemen ter grootte van
E = 2 e0 Us ,
wat volgens de quantum-mechanica gelijkstaat aan een verschil tussen de interne
frequenties van de systemen van  = E/h. Als de twee systemen trillen met
verschillende, maar in de tijd constante frequenties, dan verandert het faseverschil
ertussen lineair met de tijd als
(t) = 2  t = (2/0) Us t .
Hier verschijnt opnieuw het magnetische fluxquantum 0, waarvan de inverse 1/0 de
Josephson constante KJ wordt genoemd. Tengevolge hiervan stroomt er nu een super
wisselstroom met de zogenaamde Josephson frequentie
J = 2 e0 Us/h
door de tunneljunctie. Hiermee is het AC Josephson effect bereikt.
Josephson contacten worden gebruikt als buitengewoon snelle schakelelementen en
nauwkeurige spanningstabilisatoren. Daarenboven worden zij toegepast in
meetapparatuur voor buitengewoon kleine magnetische fluxen (SQUIDs =
Supergeleidende Quantum Interferentie Devices).
In het omgekeerde AC Josephson effect wordt er een wisselspanning met frequentie 
gezet over het Josephson contact (doorgaans door het te bestralen met microgolven). Dit
veroorzaakt in discrete stappen een spanning tussen de twee supergeleiders van de vorm
Un = n 0 ,
n = 1, 2, 3, ...
Zo werkt het Josephson contact dus als een perfecte omzetter van frequentie naar
spanning. Om deze reden wordt het wereldwijd gebruikt als constante standaard
referentiespanning in nationale metrologische instituten en in industriële ijklaboratoria.
Tot slot moet worden opgemerkt dat de Josephson effecten ook met succes
gedemonstreerd zijn met behulp van de nieuwe Hoge-Temperatuur Supergeleiders.
6. Type I / Type II Supergeleiders
Eerdergenoemde verschijnselen en hun theoretische interpretatie zoals beschreven in de
paragrafen 2 tot en met 4 hebben betrekking op zogenaamde Type I Supergeleiders, die
gekenmerkt worden doordat ze beneden Tc en Bc een volledig Meissner-OchsenfeldEffect te zien geven: een aangelegd magneetveld neemt exponentieel af binnen de
London doordringdiepte waar een superstroom stroomt om het inwendige veldvrij te
houden. Boven de kritische veldsterkte Bc worden de Cooper paren opgebroken en het
materiaal wordt weer een gewone geleider. Materialen die dit gedrag vertonen zijn
meestal zuivere metalen die echter doorgaans gekenmerkt worden door lage waardes van
de kritische temperatuur en de kritische magnetische veldsterkte. Daarom zijn zij niet erg
bruikbaar voor technische toepassingen.
In tegenstelling daarmee, vertonen zogenaamde Type II Supergeleiders (meestal
legeringen en verbindingen) een ander gedrag onder magnetisatie: beneden een eerste
kritisch magneetveld Bc1, bevinden ze zich in een zogenaamde Meissner toestand en
vertonen een volledig Meissner-Ochsenfeld-Effect (zoals een Type I Supergeleider).
Tussen dit kritische veld en een (doorgaans veel hoger) tweede kritisch veld Bc2 laten zij
een onvolledig Meissner-Ochsenfeld-Effect zien, wat betekent dat een aangelegd
magneetveld het materiaal kan binnendringen. Boven Bc2 stort de supergeleiding ineen
(zie fig. 6a).
-4πM
Bc2
Gewoon
B
Gemengd
Bc1
Bc1
Supergeleidend
toestand
Bc
Wervel
toestand
Meissner
Bc2
Gewone
toestand
B
Tc
a)
b)
T
Fig. 6: a) Geïnduceerde magnetisatie in een Type II supergeleider als functie van het aangelegde
magneetveld
b) Afhankelijkheid van de kritische magnetische veldsterktes van de temperatuur
In de tussentoestand (gemengde, Shubnikov of wervel fase) is het energetisch gunstig dat
er wervels met één magnetische fluxeenheid 0 in het materiaal bestaan. Deze wervels
zijn in de gewone, geleidende fase en worden omgeven door supergeleidende gebieden
waar supergeleidende kringstromen lopen (zie fig. 7). Als het magneetveld toeneemt van
Bc1 tot Bc2, komen er steeds meer wervels in het materiaal; omdat zij elkaar afstoten,
ontwikkelt zich een geordend twee-dimensionaal hexagonaal rooster van wervels. Dit is
ook feitelijk waargenomen onder de microscoop.
Ba
Fig. 7: Tekening van wervels in een Type II Supergeleider
De theoretische grondslag van deze verschijnselen is gelegd in het werk van V.L.
Ginzburg en L.D. Landau (1950) dat later is uitgebreid door A.A. Abrikosov (1957) en
L.P. Gor'kov (1960). Abrikosov en Ginzburg kregen in 2003 de Nobelprijs voor hun werk
toegekend (Landau was al in 1968 overleden). Men kan de essentiële eigenschappen
beschrijven door te kijken naar karakteristieke lengteschalen: eerst definiëert men een
effectieve coherentie lengte  die zowel afhangt van de "intrinsieke" coherentie lengte 0
(dit is de "omvang" van een Cooper paar), én van de gemiddelde vrije weglengte ℓ van de
elektronen in de gewone geleidingstoestand (hetgeen als volgt overeenkomt met het
begrip “weerstand”: kleine/grote ℓ betekent slechte/goede geleider) met de relatie:
1/ = 1/0 + 1/ℓ
Deze coherentie lengte moet vergeleken worden met de London doordringdiepte L. In
een pure supergeleider (met grote ℓ) isbij benadering gelijk aan 0 en veel groter dan
L. Anderzijds kan  in de "vervuilde limiet" met kleine ℓ, kleiner worden dan L waarbij
de supergeleidende toestand zó wordt aangepast dat een magneetveld in het materiaal kan
doordringen, m.a.w. dit is een Type II Supergeleider.
Dezelfde lengteschalen bepalen ook de kritische magnetische veldsterktes: Bc1 wordt
vastgelegd door L, en Bc2 door  en wel op zo’n manier dat hun product bij benadering
gelijk is aan het kwadraat van het "thermodynamische" kritische veld Bc (zie fig. 6a),
Bc1 Bc2  Bc2 .
In het ideale geval kunnen wervels vrij bewegen door het materiaal, maar kristalfouten
(als korrelgrenzen, puntfouten e.d.) hebben de neiging ze vast op hun plaats te houden.
Dit vastzetten (‘pinning’) heeft technische voordelen, omdat in dergelijke "Harde
Supergeleiders" veel hogere magneetvelden (van rond de 50 Tesla) gemaakt kunnen
worden. Bovendien kan bijna de hele dwarsdoorsnede gebruikt worden voor
stroomtransport omdat er in grote delen van het materiaal een magneetveld bestaat
waardoor het materiaal tamelijk hoge kritische stromen kan hebben. Door de materialen
op de juiste manier te behandelen, kan men van een Type I Supergeleider een (harde)
Type II Supergeleider maken.
7. Hoge-Temperatuur Supergeleiders
Hoge-Temperatuur Supergeleiders zijn supergeleiders met een kritische temperatuur die
behoorlijk wat boven de 30 K ligt. Tot 1986 was de algemene overtuiging dat, volgens de
BCS-Theorie, supergeleiding boven de 30 K niet mogelijk zou zijn. Maar in dat jaar
ontdekten J.G. Bednorz en K.A. Müller supergeleiding in perovskiet, keramische
materiaal met koperoxide (La2-xBaxCuO4) bij een kritische temperatuur tussen 30 K en 40
K (daarvoor kregen zij in 1987 de Nobelprijs). Korte tijd later werd ontdekt dat door het
vervangen van lanthanium door yttrium, dus door het maken van YBa3Cu3O7, de
kritische temperatuur verhoogd kon worden tot 93 K. Dit materiaal, ook bekend als
YBCO of de 123-verbinding, is nu een van de meest uitvoerig bestudeerde hogetemperatuur supergeleiders.
Fig. 8: Ontwikkeling van de hoge-temperatuur supergeleiding
Op deze manier kwam afkoeling met vloeibare stikstof (kookpunt bij 77 K) binnen
bereik, waardoor technische toepassingen veel eenvoudiger en goedkoper werden. In de
daarop volgende jaren werden veel andere, verwante materialen ontdekt met zelfs nog
hogere kritische temperaturen; het officiële record (sinds maart 2007) staat op Tc = 138 K
voor Hg0.8Tl0.2Ba2Ca2Cu3O8. Onder hoge druk bereikt de kwikverbinding
HgBa2Ca2Cu3O8 zelfs een kritische temperatuur van boven de 160 K. Ook is er een
octrooi genomen op een materiaal met een kritische temperatuur van tegen de 150 K.
Jammer genoeg is het mechanisme achter de hoge-temperatuur supergeleiding nog steeds
niet ontraadseld, hoewel sommige gemeenschappelijke kenmerken van de hoge-Tc
koperoxides al gevonden zijn: alle koperoxides zijn zonder verontreiniging
antiferromagnetische isolatoren, bij verontreiniging worden ze metallisch en dus
supergeleidend. De verontreiniging heeft een optimale concentratie beneden of boven
welke Tc lager is. De ladingsdragers van de meeste hoge-Tc supergeleiders zijn gaten (=
ontbrekende elektronen). De gemeenschappelijke structuurelementen zijn CuO2 vlakken
die hoofdzakelijk verantwoordelijk zijn voor de superstroom. Een mogelijke kandidaat
voor de vorming van Cooperparen (die van wezenlijk belang zijn voor de supergeleiding)
zou een antiferromagnetische spin-spin-wisselwerking kunnen zijn, terwijl fononen
(zoals in de BCS-Theorie) hoogstwaarschijnlijk uitgesloten zijn. Er wordt nog steeds hard
gewerkt om een fundamentele theorie van de hoge-temperatuur supergeleiding te vinden.
Tot slot: in 1964 werd de hypothese naar voren gebracht dat organische materialen
supergeleiding zouden vertonen bij zeer hoge kritische temperaturen. Deze verwachting
is echter sindsdien niet bevestigd, al zijn er wel organische supergeleiders gevonden met
kritische temperaturen rond de 10 K.
Bronvermelding
Delen van dit artikel zijn in aangepaste vorm
overgenomen uit W. Buckel en R. Kleiner,
Superconductivity: fundamentals and
applications, Wiley, Weinheim (2003), met
name enkele figuren.
Ook een manuscript van C. Ambrosch-Draxl
voor een college over supergeleiding aan de
Universiteit van Graz was heel nuttig. Figuren
2, 4a en 6a zijn overgenomen uit Ch. Kittel:
Introduction to Solid State Physics, 7th ed.,
Wiley, New York (1996).
Figuur: 3D-model van YBCO
http://commons.wikimedia.org/wiki/Image:YBCO-3Dballs.png