Normale Verdeling Inleiding

Normale Verdeling Inleiding
© Wisnet-hbo
update maart 2010
1 De Normale verdeling
De Normale Verdeling beschrijft het gedrag van een continue kansvariabele x.
Om kansen te berekenen, moet de dichtheidsfunctie gegeven zijn.
De grafiek van de dichtheidsfunctie van een normale verdeling is "klokvormig".
Oppervlakken onder de grafiek van de dichtheidsfunctie geven dan de kansen aan.
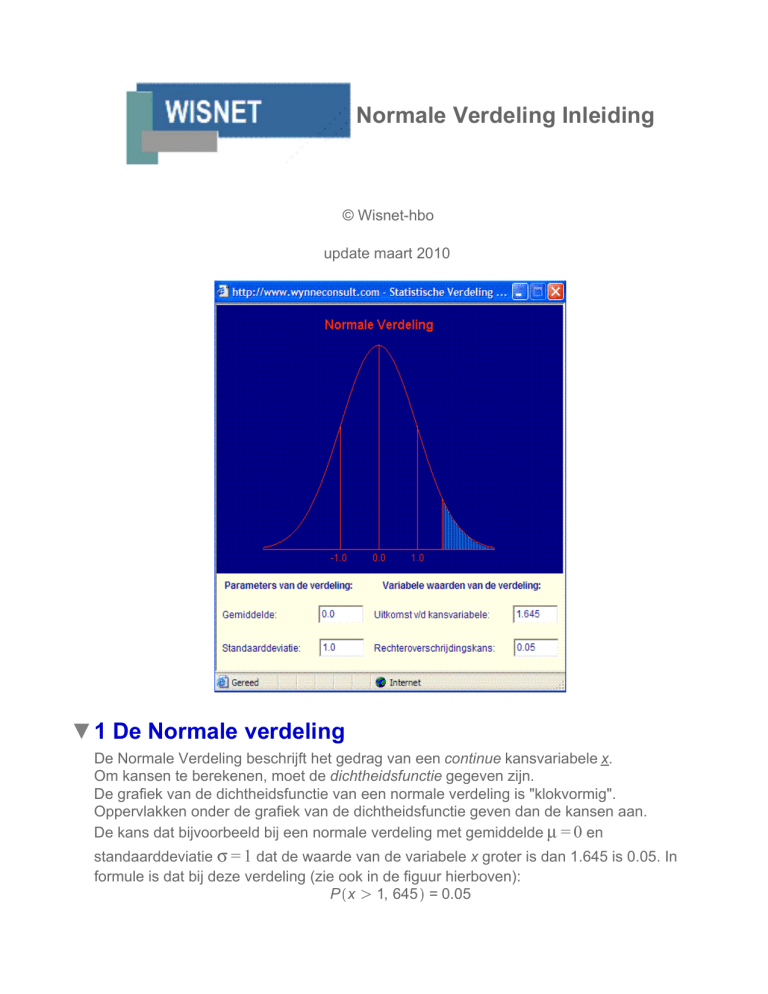
De kans dat bijvoorbeeld bij een normale verdeling met gemiddelde μ = 0 en
standaarddeviatie σ = 1 dat de waarde van de variabele x groter is dan 1.645 is 0.05. In
formule is dat bij deze verdeling (zie ook in de figuur hierboven):
P x O 1, 645 = 0.05
2 Eigenschappen van de standaardnormale verdeling
Bij de standaardnormale verdeling heeft de kansvariabele een gemiddelde waarde van
μ = 0 en standaarddeviatie σ = 1.
De bijbehorende kromme heeft een klokvorm en is de grafiek van de kansdichtheidsfunctie:
1 2
x
2
K
1
e
2π
De grafiek is symmetrisch t.o.v. de lijn door μ = 0 en links en rechts van de top zijn
buigpunten.
Als we het over de normaalverdeling hebben met deze eigenschap van μ en σ, dan spreken
we liever over de kansvariabele z.
Deze buigpunten bevinden zich precies bij x = 1 en bij x =K1. (In feite dus bij z = 1 en bij
z =K1)
Dat wil zeggen precies bij de waarde van de standaarddeviatie σ links en rechts.
De gehele oppervlakte onder de grafiek is precies gelijk aan 1.
3 Standaarddeviatie σ
Als de standaarddeviatie niet gelijk is aan 1, wordt de kromme vervormd.
De kansvariabele noemen we nu x.
Vermenigvuldig met σ ten opzichte van de verticale as (als σ bijvoorbeeld twee maal zo
x
groot wordt, dan wordt de grafiek twee maak zo breed en dus vervang je x door .
σ
1
σ 2π
1
K
2
e
x
σ
2
Omdat de oppervlakte onder de kromme gelijk moet blijven aan 1, wordt de kromme lager
als deze breder wordt.
De hele functie moet dus gedeeld worden door σ
Naarmate dus σ groter wordt, wordt de kromme lager én breder.
De waarde van σ correspondeert met de buigpunten van de grafiek.
In de figuur loopt σ van 1 (smalle grafiek) tot 4 (brede grafiek).
0.18
0.16
0.14
0.12
0.10
0.08
0.06
0.04
0.02
K10
K5
0
5
10
4 Gemiddelde waarde
Als de gemiddelde waarde niet gelijk is aan 0 maar aan een andere waarde bijvoorbeeld
μ = 5, dan is het enige dat er met de grafiek gebeurt, dat de grafiek een horizontale
verplaatsing ondergaat.
Als de grafiek 5 naar rechts gaat, dan vervang je in de formule x door x - 5.
Als de waarde van de standaarddeviatie σ weer loopt van 1 tot 4, wordt de kromme weer
breder en lager, maar nu ligt de verticale symmetrieas bij μ = 5 .
1
σ
2π
1
K
2
e
x K5
2
σ
2
0.3
0.2
0.1
K5
0
5
10
15
5 Oppervlakken en kansen
De oppervlakte onder de kromme geeft de kans weer.
Kijk altijd of je met de grenswaarde links of rechts van het gemiddelde zit en bekijk of de
oppervlakte ongeveer de gevraagde kans weergeeft.
Het is belangrijk om aan te geven hoeveel maal de standaarddeviatie σ je links of rechts uit
het midden zit.
Deze excentriciteit z die te maken heeft met de standaardnormale verdeling geeft dus aan
"het aantal malen σ uit het midden".
Vergelijk de volgende kansen met links de standaardnormale verdeling en rechts de
normale verdeling met bepaalde μ en σ.
De vorm van de kromme is steeds dezelfde, hooguit breder (en lager) en/of horizontaal
verschoven.
In de figuur is ook de grootte van σ aangegeven.
Standaardnormale verdeling
Normale verdeling
0.18
0.3
0.14
0.2
0.10
0.06
0.1
0.02
K3
K2
K1
0
1
2
0
3
2
4
6
8
10
Normale verdeling met μ = 0 en σ = 1
Normale verdeling met μ = 5 en σ = 2
P z O 0.5 = 0.3085
P x O 6 = 0.3085
(De grenswaarde heeft excentriciteit z = 0.5) (De grenswaarde heeft excentriciteit z = 0.5)
P z ! 0.5 = 1 K0.3085 = 0.6915
P z ! 6 = 1 K0.3085 = 0.6915
Standaardnormale verdeling
Normale verdeling
0.04
0.3
0.03
0.2
0.02
0.1
0.01
0
K3
K2
K1
0
1
2
3
130
140
150
160
170
Standaardnormale verdeling met μ = 0 en σ
=1
Normale verdeling met μ = 150 en σ = 8
P z !K1.5 = 0.0668
P x ! 138 = 0.0668
(De grenswaarde heeft excentriciteit
z =K1.5)
(De grenswaarde heeft excentriciteit
z =K1.5)
P z OK1.5 = 1 K0.0668 = 0.9332
P z O 138 = 1 K0.0668 = 0.9332
5.1 Gebruik van de tabel van de standaardnormale verdeling
Bekijk bovenstaande figuur.
Rechts zien we schematisch de kans dat x kleiner is dan 138. Deze kans is voorgesteld
door het gele oppervlak.
Deze verdeling heeft gemiddelde μ = 150 en standaarddeviatie σ = 8.
Er moet berekend worden hoe groot de kans is dat x kleiner is dan 138.
We "vertalen" de situatie rechts naar in feite dezelfde situatie links.
Echter links is het de standaardnormale verdeling (met μ = 0 en σ = 1)
Verder komen de figuren verhoudingsgewijs met elkaar overeen.
Bekijke nu hoe groot de excentriciteit is rechts.
Dat wil zeggen hoeveel maal de waarde van zit je van het midden af: en dat is hier 1.5 × 8
dat je uit het midden gerekend, naar links zit.
150 K138
12
3
Immers
=
=
= 1.5 De excentriciteit is dus z = -1.5
8
8
2
In gedachten klappen we deze situatie om naar rechts zodat het gele staartje naar rechts
komt.
Als je nu de waarde van de excentriciteit weet: z = 1.5 (en nu dus positief omdat je in
gedachten omgeklapt hebt naar rechts),
kun je in de tabel van de Standaardnormale verdeling (zie figuur hieronder) de kans aflezen
en die is 0.0668.
Als je de oppevlakte van het grijze gedeelte wilt weten, kan dat gemakkelijk als je bedenkt
dat de oppervlakte onder de hele grafiek gelijk moet zijn aan 1.
Als de excentriciteit in twee decimalen is opgegeven, kun je de in de tabel kijken om de
kans uit te rekenen:
P(z >1.54) = 0.0618. Je kijkt dan in de kolom (bij 0.04) voor de tweede decimaal van z op
de regel van z = 1.5.
script van de figuur