opg3

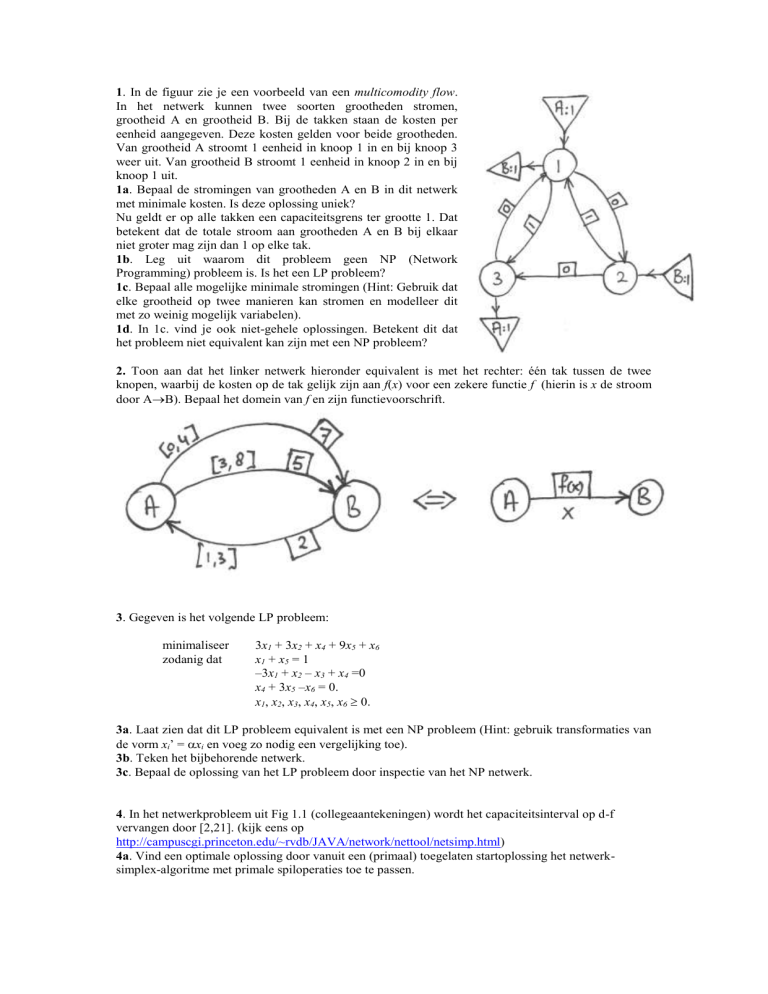
1. In de figuur zie je een voorbeeld van een multicomodity flow.
In het netwerk kunnen twee soorten grootheden stromen,
grootheid A en grootheid B. Bij de takken staan de kosten per
eenheid aangegeven. Deze kosten gelden voor beide grootheden.
Van grootheid A stroomt 1 eenheid in knoop 1 in en bij knoop 3
weer uit. Van grootheid B stroomt 1 eenheid in knoop 2 in en bij
knoop 1 uit.
1a. Bepaal de stromingen van grootheden A en B in dit netwerk
met minimale kosten. Is deze oplossing uniek?
Nu geldt er op alle takken een capaciteitsgrens ter grootte 1. Dat
betekent dat de totale stroom aan grootheden A en B bij elkaar
niet groter mag zijn dan 1 op elke tak.
1b. Leg uit waarom dit probleem geen NP (Network
Programming) probleem is. Is het een LP probleem?
1c. Bepaal alle mogelijke minimale stromingen (Hint: Gebruik dat
elke grootheid op twee manieren kan stromen en modelleer dit
met zo weinig mogelijk variabelen).
1d. In 1c. vind je ook niet-gehele oplossingen. Betekent dit dat
het probleem niet equivalent kan zijn met een NP probleem?
2. Toon aan dat het linker netwerk hieronder equivalent is met het rechter: één tak tussen de twee
knopen, waarbij de kosten op de tak gelijk zijn aan f(x) voor een zekere functie f (hierin is x de stroom
door AB). Bepaal het domein van f en zijn functievoorschrift.
3. Gegeven is het volgende LP probleem:
minimaliseer
zodanig dat
3x1 + 3x2 + x4 + 9x5 + x6
x1 + x5 = 1
–3x1 + x2 – x3 + x4 =0
x4 + 3x5 –x6 = 0.
x1, x2, x3, x4, x5, x6  0.
3a. Laat zien dat dit LP probleem equivalent is met een NP probleem (Hint: gebruik transformaties van
de vorm xi’ = xi en voeg zo nodig een vergelijking toe).
3b. Teken het bijbehorende netwerk.
3c. Bepaal de oplossing van het LP probleem door inspectie van het NP netwerk.
4. In het netwerkprobleem uit Fig 1.1 (collegeaantekeningen) wordt het capaciteitsinterval op d-f
vervangen door [2,21]. (kijk eens op
http://campuscgi.princeton.edu/~rvdb/JAVA/network/nettool/netsimp.html)
4a. Vind een optimale oplossing door vanuit een (primaal) toegelaten startoplossing het netwerksimplex-algoritme met primale spiloperaties toe te passen.
4b. Gebruik de optimale oplossing van het oorspronkelijke probleem (zie week 3 sheet 17) en voeg een
tak toe om een toelaatbare oplossing te maken die als startoplossing is te gebruiken. Vind met het
primale algoritme de optimale oplossing
4c. Gebruik de optimale oplossing van het originele probleem en laat zien dat die voor dit probleem
duaal toelaatbaar is (alle schaduwprijzen niet-negatief). Gebruik deze oplossing als startoplossing voor
het algoritme met duale spiloperaties.