PDF-slides Straling

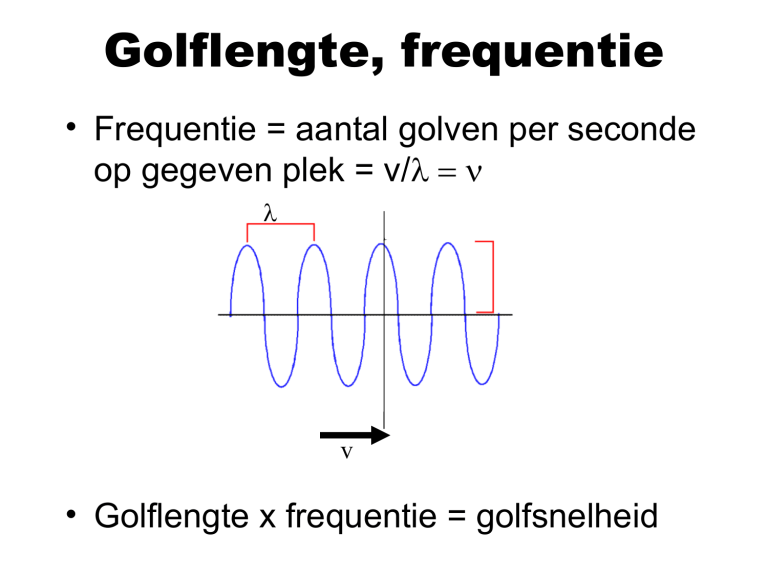
Golflengte, frequentie
• Frequentie = aantal golven per seconde
op gegeven plek = v/λ = ν
λ
v
• Golflengte x frequentie = golfsnelheid
Snelheid van het licht
Manen van Jupiter (Römer 1676)
– Eclipsen van Io zijn te vroeg of te laat,
afhankelijk van stand Aarde-Jupiter
– Reistijd van het licht over
de straal van de aardbaan
(1 AE) = § 8 minuten
– C = 300,000,000 m/s
Huygens' principe
• Golffront
• Verklaart
diffractie (golven kunnen om rand heen)
interferentie
Dubbele spleet: Young expt.
• Interferentie
– Coherent: licht
– Destructief: donker
• Toont dat licht zich gedraagt als golf
– Kunt hiermee golflengte meten
• Ook refractie (breking), diffractie zijn
eigenschappen van golven
Breking (refractie)
• Maxwell c2 = 1/(µ0 ε0)
• In een medium is c vertraagd – breking
• Refractie-index n=cvacuum/c > 1
Afstand tussen pieken
is c/ν
i
X-afstand tussen
pieken zelfde in beide
media
X
r
ν zelfde
)sin i / c1 = sin r / c2
dispersie
• n hangt af van golflengte ) dispersie )
spectrum
• Zichtbaar licht slechts klein deel van het
electromagnetische spectrum
Doppler Effect
•
Golven krijgen andere frequentie als de waarnemer of bron beweegt
Roodverschuiving (v>0)
bron
1/ν0
λ0
t
λ=λ0(1+v/c)
Bewegende
bron
ν=ν0/(1+v/c)
1/ν
λ
Relativistisch:
λ=γλ0(1+v/c)
Gradient 1/v
ν=γ−1ν0/(1+v/c)
λ0
Gradient=§1/c
Stationaire
waarnemer
1/ν0
v/ν0
x
Fotonen
• Quantummechanica: licht bestaat uit quanta
– Energy per quantum = hν
(h=constante van Planck = 6.6£10-34Js)
– Foto-electrisch effect; Compton verstrooiing
• Fotonen geven (deel van) energie aan electron
• Gevoelige astronomische waarnemingen zijn
letterlijk foton-tellingen
– Bijv: van Wega ontvangen we ongeveer
10000
fotonen/s/cm2/nm in groen licht
– Bij zwakke bronnen enkele fotonen per uur!
Intensiteit van straling
• Intensiteit I = hoeveelheid uitgestraalde energie
per:
– tijdsinterval
– frequentie-interval
– oppervlakte-eenheid van de bron
– steradiaan (eenheid bolhoek)
• Eigenschap van een stralingsbron
• Eenheden W Hz-1 m-2 sr-1
• Bijv. totale energie/s ´ lichtkracht L uit
een sferische ster =2π (4π R2) s I(ν) dν
Flux(-dichtheid) van een bron
• Hoeveelheid ontvangen straling per:
– eenheid oppervlakte
– eenheid tijd
– eenheid frequentie (monochromatische flux)
• Hangt af van locatie van de waarnemer
• Eenheid: W Hz-1 m-2 of W m-2
• Bv.: flux van een ster van helderheid L is
L/(4π D2) als de ster op afstand D staat
Spectraallijnen
Elektronen in atomen hebben wel-bepaalde
quantum-mechanische `banen’
– Gequantizeerde energieniveaus
– Overgangen gaan gepaard met emissie of
absorptie van een foton met precies de goede
energie:∆ E=hν
– Bijv. waterstof-atoom: banen met energie
– Dus fotonen met golflengtes
Het waterstofspectrum
Energie van electron
• Lyma-reeks na=1
– Lyα: nb=2
λ=121.6nm
– Lyβ: nb=3
λ=102.6nm
n=1 – Lyγ: nb=4
n=4
!
– Etc
n=3
n=2 • Balmer-reeks
– Hα: nb=3
– Hβ: nb=4
UV
λ=97.3nm
λ1=91.2nm (ionizatie)
na=2
OPTISCH
λ=656.3nm
λ=486.3nm
n=1 • Paschen na=3; Brackett na=4
IR
Moleculaire lijnen
• Veel meer vrijheidsgraden dan een
atoomkern + elektronen
• Buig, strek, rotatie-modes met eigen
gequantizeerde energieniveaus
• Kleine energieverschillen ! dichte
`bosjes’ van lijnen, voornamelijk IR
Vorming van spectra
• Emissielijnen
– Worden gevormd als atomen/ionen worden aangeslagen
(bv. door botsingen). De-excitatie door middel van fotonemissie geeft lijnspectrum.
– Toegestane transities gebeuren na ~10-8 s
– Verboden transities zijn meta-stabiel en gebeuren veel
langzamer: als de dichtheid van de atomen te hoog is vindt
de-excitatie via botsingen plaats
Een ‘planetaire nevel’
• Spectrum bestaat uit emissielijnen van
waterstof en zuurstof
– Zuurstoflijn is ‘verboden’
M27
Vorming van spectra
• Absorptielijnen
– Worden gevormd als atomen/ionen worden aangeslagen
door fotonen. Achtergrondlicht van bepaalde golflengtes
wordt dan geabsorbeerd.
– De-excitatie gebeurt ook door middel van foton-emissie,
maar
• Kan andere overgang zijn
• Emissierichting is willekeurig
Het zonnespectrum: absorptielijnen
(door buitenste laag van de zon)
Vorming van spectra
Ionizatie
– Als de energie van een foton hoog genoeg is kan een
elektron worden bevrijd uit een atoom/ion
– De energie van een vrij elektron is niet gequantizeerd
– Dus alle fotonen met energie groter dan de ionizatie-energie
kunnen worden geabsorbeerd
– Bijv waterstof: alle fotonen met λ<91.2nm worden door
neutraal waterstofgas geabsorbeerd.
Interpretatie van lijnsterktes
• Gecompliceerd:
– Aantal overgangen van toestand A naar
toestand B hangt af van
•
•
•
•
Aantal atomen
Fractie daarvan met dezelfde ionizatie als A
Fractie daarvan in toestand A
Quantum-mechanische beschrijving van de
overgang
– Bijv. Hβ (n=4 ! 2 van waterstof)
• Temp te laag: alle H in grondtoestand
(n=2, niet in n=4)
• T te hoog: veel H geionizeerd ! geen atomen
• Hoge dichtheid: veel de-excitatie door botsingen
– Hangt af van T, compositie, en dichtheid
Verschillende
‘spectrale
types’
Koudere
steratmosfeer
Balmer reeks
zon
Lijnbreedtes
• Intrinsiek: quantummechanica
• Dopplerverbreding
– Hoge temperatuur  snelle beweging van atomen
(mv2~2kT) dus δλ/λ = v/c ~ (2kT/mc2)1/2
voor waterstof op 6000K is δλ/λ ongeveer 3£10-5.
– Onopgeloste bewegingen, bv rotatie van een ster
• Stark effect
– Nabije atomen verstoren energieniveaus ! bij hoge
dichtheid bredere lijnen
• Zeeman effect
– Magneetvelden verstoren energieniveaus van electronen
(want het zijn dipooltjes).
Zwart-Lichaam-straling
• Thermisch evenwicht: voortdurende uitwisseling van energie
tussen deeltjes
– Temperatuur / gemiddelde energie per deeltje (mv2/2=kT)
• Straling van zo’n zwart lichaam (dat alles absorbeert, verwerkt en
weer uitstraalt) volgt Planck spectrum
• Bij lage ν of hoge T wordt dit (Rayleigh-Jeans formula)
• Piek van Iλ ligt op λ=0.002898/T m (wet van Wien)
– rood-heet ! wit-heet ! blauw-heet
• Totale intensiteit = s I(ν)dν = σ T4 (wet van Stefan-Boltzmann)
σ=5.669£10-8 W m-2 K4.
Het Planck spectrum
Wien
R-J
Zwart-Lichaam-straling
• Wet van Wien
λ=0.002898/T m
λ
T
Zon
Aarde
Kosmische
achtergrond
5700K
500nm
300K
10µm
3K
1mm
Magnitudes
• Astronomen meten relatieve fluxen
– F1/F2 wordt uitgedrukt als logaritme:
m2-m1 = 2.5 log(F1/F2)
– NB omgekeerde schaal!
– Factor 100 in flux ´ 5 magnituden verschil
– Nulpunt is de heldere ster Vega
• Absolute magnituden meten lichtkracht
– Magnitude die object zou hebben geplaatst
op 10pc = 3.086£1017m afstand.
Het spectrum van de hemel
Extragalactisch licht
1.
2.
3.
3K thermische straling
Sterlicht
Melkwegkernen
1
2
3