Extra stof M2H2 Omzet , kosten en winst

M2 H2.7
Extra stof: break even
Print deze paragraaf uit en maak vervolgens de bijbehorende vragen.
Natuurlijk willen ondernemers weten hoeveel producten je minimaal moet verkopen om uit de kosten
te komen. Je wilt immers op zijn minst quitte spelen. Deze productieomvang wordt het break-evenpunt genoemd. Een voorbeeld:
Prins nv produceert fondue-sets, raclette-grillen en steengrillen. De onderneming wil een aantal
apparaten in een speciale luxe designuitvoering op de markt brengen. Prins gaat bij de steengrill uit
van de volgende gegevens:
-
Prins verkoopt de steengrillen voor een prijs (p) van € 100 per stuk;
De variabele kosten per steengrill bedragen € 75 per stuk;
De constante kosten bedragen € 100.000;
Productiecapaciteit is 6000 stuks.
De totale omzet (TO) is dan gelijk aan: TO = 100q
De totale kosten (TK) zijn dan:
TK = 75 q + 100.000
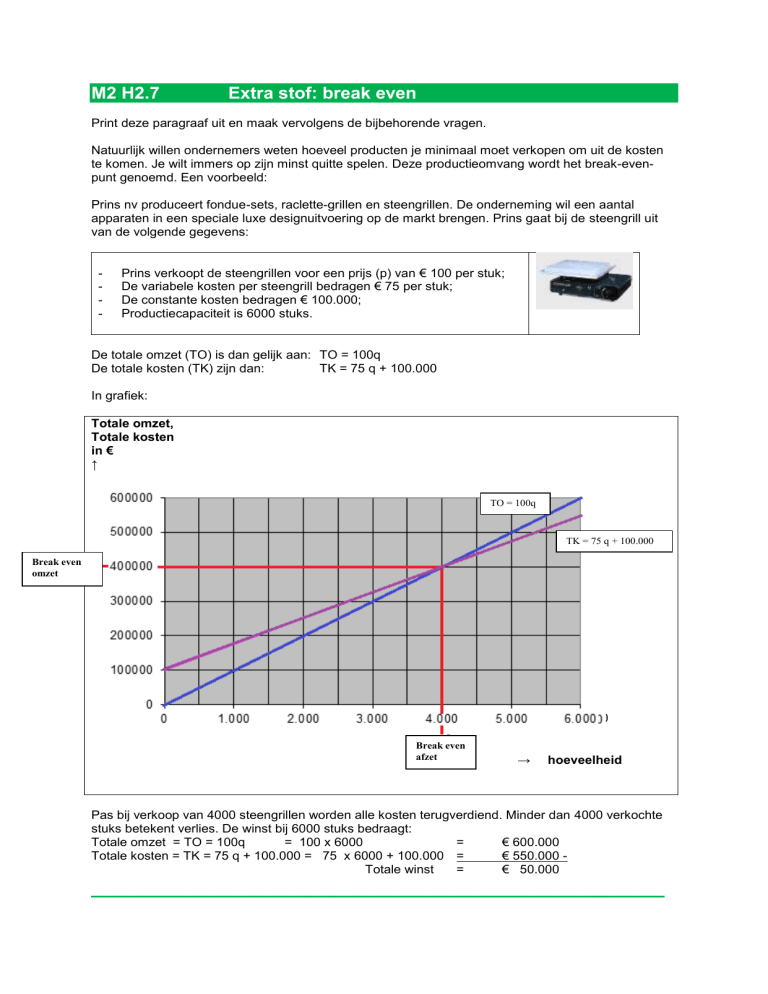
In grafiek:
Totale omzet,
Totale kosten
in €
↑
600000
TO = 100q
500000
Break even
omzet
TK = 75 q + 100.000
400000
300000
200000
100000
0
0
1,000
2,000
3,000
4,000
Break even
afzet
5,000
→
6,000
hoeveelheid
Pas bij verkoop van 4000 steengrillen worden alle kosten terugverdiend. Minder dan 4000 verkochte
stuks betekent verlies. De winst bij 6000 stuks bedraagt:
Totale omzet = TO = 100q
= 100 x 6000
=
€ 600.000
Totale kosten = TK = 75 q + 100.000 = 75 x 6000 + 100.000 =
€ 550.000 Totale winst
=
€ 50.000
__________________________________________________
Gevraagd
JEROEN PENDERS BV produceert antieke houten kasten. Jeroen wil een nieuwe kast op de markt
brengen. Hij weten hoeveel kasten hij minimaal moet produceren om op zijn minst quitte te spelen.
p = € 425 per stuk.
2 000 kasten per maand.
TK = 300q + 100.000
Penders verkoopt de kasten voor:
De productiecapaciteit is:
De functie v/d totale kosten luidt:
TK = totale kosten
q = het aantal kasten
1
De variabele kosten per kast bedragen:
A €
300
B €
425
C € 2.000
D € 100.000
Hieronder staan vier verschillende grafieken, die de gegevens van Penders zouden weergeven.
I.
II.
TO
TK
TO
TK
600000
500000
400000
TO
300000
200000
TK
100000
0
0
400
800
1,200
600000
500000
400000
300000
200000
100000
0
TK
TO
01,000
2,000
3,000
4,000
5,000
6,000
III.
IV.
TO
TK
TO
TK
600000
600000
500000
500000
TO
400000
300000
TK
300000
200000
200000
100000
100000
0
TO
0
0
2
TK
400000
400
800
Welke weergave is juist?
A Grafiek I
B Grafiek II
C Grafiek III
D Grafiek IV
1,200
0
400
800
1,200
3
Hoeveel kasten moet Penders minimaal per maand verkopen om zijn kosten te dekken.
A
600
B
800
C 1200
D 2000
4
Bereken hoeveel winst Penders per maand maximaal kan maken.
A 1200 x € 425 + 1200 x € 300 + € 100.000
B 1200 x € 425 + 1200 x € 300 – € 100.000
C 1200 x € 425 – 1200 x € 300 + € 100.000
D 1200 x € 425 – 1200 x € 300 – € 100.000
5
Bereken hoeveel verlies Penders bij verkoop van 400 stuks per maand zou maken.
A € 390.000
B € 190.000
C € 190.000
D € 50.000
__________________________________________________
Antwoorden
1
A
2
B, Grafiek II
3
B, 800; Daar geldt TO = TK
4
D, € 50.000
5
D, 400 x € 425 – 400 x € 300 – € 100.000 = – € 50.000
__________________________________________________