1) De eigenschappen van gassen en de kinetische

1) De eigenschappen van gassen en de kinetische gastheorie.
De gastoestand is de eenvoudigste toestand van de materie.
pV = nRT
Ideale gaswet:
 experimenteel bekomen
p = druk
n = aantal mol
V = volume
R = gasconstante
T = temperatuur (in Kelvin)
Een ideaal gas is een gas waarvan de intermoleculaire krachten en het V kan verwaarloosd worden
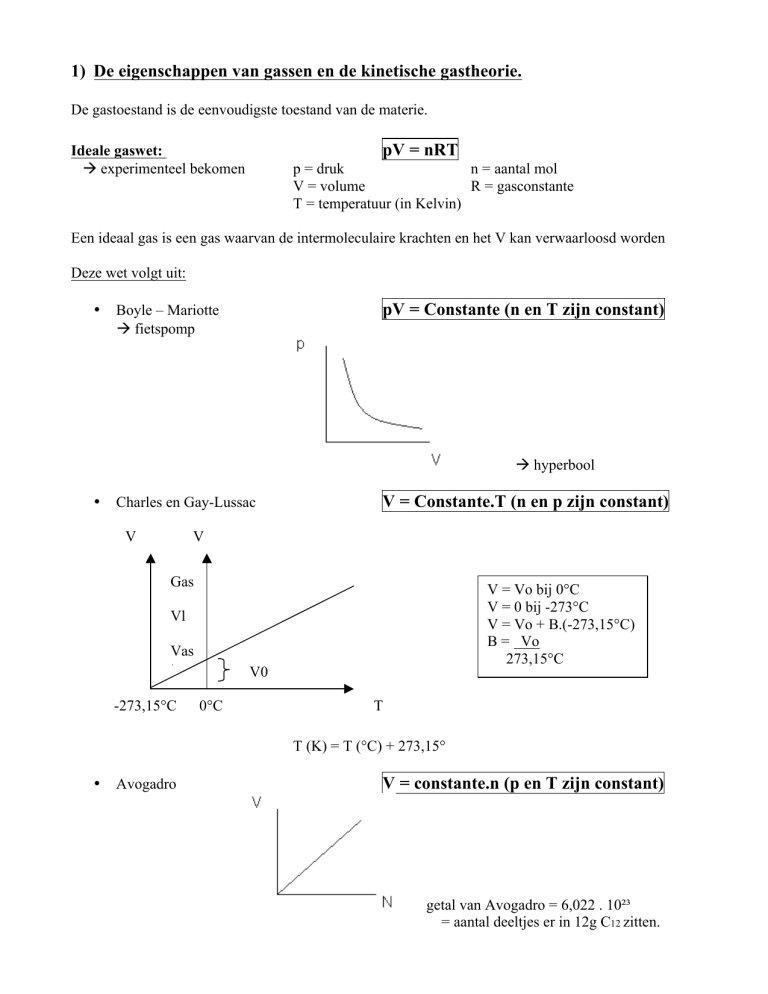
Deze wet volgt uit:
•
pV = Constante (n en T zijn constant)
Boyle – Mariotte
 fietspomp
 hyperbool
•
Charles en Gay-Lussac
V
V = Constante.T (n en p zijn constant)
V
Gas
V = Vo bij 0°C
V = 0 bij -273°C
V = Vo + B.(-273,15°C)
B = Vo
273,15°C
Vl
Vas
t
-273,15°C
V0
0°C
T
T (K) = T (°C) + 273,15°
•
Avogadro
V = constante.n (p en T zijn constant)
getal van Avogadro = 6,022 . 10²³
= aantal deeltjes er in 12g C12 zitten.
Naar gelang de omstandigheden kan elk gas ideaal of reëel zijn.
Reële gassen.
Experimenteel: er zijn afwijkingen van de ideale gaswet bij hoge druk en/of lage temperatuur.
 volume is groter dan verwacht op grond van de ideale gaswet.
Aanpassingen:
- Van der Waals: als n = 1  p = RT - a
V-b V²
•
•
•
a = intermoleculaire attractie
b = volume van de gasmoleculen
V = volume van het vat.
Deeltjes zijn geen mathematische punten, maar hebben een eigen volume (b)
Ze trekken elkaar aan of stoten elkaar af (a)
Bij een groot volume = p = RT
V
Kinetische energie.
Mechanisch model van een ideaal gas:
- moleculen zijn in willekeurige beweging (diffusie),
- moleculen worden voorgesteld door mathematische punten (b = 0)
- Noch onderlinge aantrekking, noch afstoting (a = 0 & b = 0)
- Moleculen botsen onderling en met de wand.
Uitgaande van Maxwell
pV = 1/3 nM<V>²
pv = nRT
Ek = nRT
<v> ~ 1/vkw(M)




M = molaire massa
pV = kinetische energie
½ M<V>² = nRT
1/3 nM<V>² = nRT
M<V>² = 3RT
<V> = vkw(3RT/M) = Diffusie - en effusiesnelheid
 voor gassen is die evenredig met de
moleculaire snelheid. (GRAHAM)
v ~ vkw(T)  T is een interpretatie van snelheid van de beweging.
Uit <V> = vkw (3RT/M)  als T stijgt dan stijgt v
 als M stijgt dan daalt v
Maxwell – Boltzmann verdeling van moleculaire snelheden en energieën.
 invloed van de T speelt een grote rol in de kinetische en thermodynamische beschouwingen
 T stijgt als het aantal moleculen met zeer hoge snelheid stijgt.
 moleculen met een heel hoge snelheid gaan botsen en reageren.
Verband tussen Ek (1/2 mv²) en snelheid.
De verandering van atmosferische druk met de hoogte.
Patm stijgt met 1atm
Per 10m vloeistof
p = po . exp (-Mgh/RT)  exponentiële vermindering van de atmosferische druk met hoogte.
Verandering van druk met hoogte.
Dp/dh = -dg (dichtheid . vrije val versnelling)
Voor vloeistoffen: p = -dgh + C (= po)
p = po - dgh
 d is onafhankelijk van de diepte
Voor gas: d : Mp/RT
 dp/dh = -(Mg/RT)p
 p = po . exp (-Mgh/RT)
 d verandert met hoogte
of
dp/p = -(Mg/RT)dh
2) De reactiewarmte en het verband met de bindingsenergie.
Reactiewarmte = H = enthalpie
E is een toestandsfunctie, onafhankelijk van de gevolgde weg
E = inwendige energie = toestandsfunctie
∆E = Eeind – Ebegin ≠ toestandsfunctie
∆E = Q + W + andere vormen
Q = E die wordt overgedragen wegens het verschil in T tussen systeem en omgeving
W = E die geleverd (of opgenomen) wordt door het systeem als het gevolg van ∆V (W= -p∆V)
 Q en W zijn geen toestandsfuncties, maar hun som wel
Enthalpie = E bij constante druk = warmteuitwisseling met de omgeving bij constante druk
Arbeid kan volledig omgezet worden in warmte (schaatsen) maar niet omgekeerd (motor)
H is een toestandsfunctie  ∆H is onafhankelijk van de gevolgde weg
∆H = Heind – Hbegin
∆E = ∆H- p∆V
 p∆V = expansiearbeid als gevolg van ∆V
 ∆E ≈ ∆H
H2O (vl)  H2O (G)
 is te verwaarlozen
∆H (verdampen) = 40,7 kJ/mol bij 100°C∆H = +
∆H = +
ENDOTHERM
Systeem
∆H = -
EXOTHERM
Endotherm proces: het systeem (of reactie) neemt bij constante T warmte op uit de omgeving
 ∆H = +
vb: smelten
H2O (V)  H2O (vl)
∆H = 6 kJ/mol
Exotherm proces: het systeem (of reactie) geeft bij constante T warmte af aan de omgeving
 ∆H = vb: stollen
H2O (Vl)  H2O (v)
∆H = - 6 kJ/mol
Loopt een chemische reactie (of een fysisch proces) af in een geïsoleerd systeem dan zal bij:
Een endotherm proces de T van het systeem dalen (vb smelten ijs in glas water)
Een exotherm proces de T van het systeem stijgen (vb vlam van een kaars)
Enthalpieverandering is geen criterium voor het al dan niet spontaan verlopen van een proces.
Het verschil in reactiewarmte kan verklaard worden door het verschil in aggregatietoestand. (V,Vl,G)
Bindingsenergie.
= Energieverandering die optreedt bij het breken in de gasfase van 1mol bindingen ter vorming
van atomen.
 BE is altijd endotherm.
Vb: H2 (G)  2H (G)
BE = + 436 kJ/mol
Verband:
BE laat toe reactiewarmtes te berekenen.
De warmte die vrijkomt bij chemische reacties hangt dus samen met het breken en vormen van
chemische bindingen
Vb: H2 + Cl2  2HCl
BE = 431 x 2 = 862 kJ/mol
Bij exotherme reacties worden zwakke bindingen gebroken
3) De fysische eigenschappen van de atomen uitgaande van de atomaire structuur.
Tabel van Mendeliev.
•
Atoomstraal
o Stijgt binnen de groep van boven naar beneden
 Bij een nieuwe schil stijgt de atoomstraal
• vb: H < Na
o Stijgt binnen de periodes van rechts naar links
 De kernlading en de aantrekking stijgen  dus ze gaan dichter bij elkaar liggen
• Vb: F < O
•
Ionstraal
o Straal kation (positief geladen ion) < straal atoom
 Vb: Na+ < Na
o Straal anion (negatief geladen ion) < straal atoom
 Vb: Cl < Cl-
•
Ionisatieënergie
o Is de energie die nodig is om een elektron weg te trekken bij de vorming van ionen.
 Dit kost E dus ∆H is altijd +
• IE ≈ 1/atoomstraal
 Als de R stijgt, daalt de IE (e- kunnen dan makkelijker weg) en omgekeerd.
 Stijgt van links naar rechts en van onder naar boven
 Vb: Na (G)  Na+ (G) + E- (G)
•
Elektronaffiniteit.
o Is de E die afgegeven wordt om een elektron op te nemen bij de vorming van ionen.
 ∆H kan + en – zijn.
• EA = 1/atoomstraal
 Vb: Cl (G) + e- (G)  Cl- (G)
IE en EA evolueren in dezelfde richting: van links naar rechts en van boven naar onder.
•
Elektronegativiteit.
Vorming van:
Kationen: elementen met lage IE en lage EA
Anionen: elementen met hoge IE en hoge EA
 Elektronegativiteit = constante x [(IE + EA) / 2]
• EN van een atoom is een getal (geen dimensies)
• Het geeft de tendens aan van het atoom om (bindings)elektronen naar
zich toe te trekken.
4) De ionische, de covalente binding en hun verband.
Ionische bindingen.
Dit zijn chemische waarbij tussen 2 atomen elektronen worden overgedragen
Treed op tss een uitgesproken metaal (vb Na) en een uitgesproken niet-metaal (vb Cl)  ∆En = groot.
Vb. Na+ + Cl-  NaCl
Roosterenergie.
Dit is de energie die vrijkomt bij de vorming van het ionrooster, uitgaande van ionen in de gasfase.
De vormingswarmte kan berekend worden: vb: KCl (v)
K (v) + 1/2 Cl2 (g)  KCl (v) ∆Hf = - 437 kJ/mol
Stap I: We brengen de elementen in atomaire toestand in de gasfase:
K (v)  K (g)
1/2 Cl2 (g)  Cl (g)
∆Hsublimatie = + 89 kJ
∆Hbindingsenergie = + 122 kJ
Stap II: Vervolgens vormen we ionen in de gasfase:
K (g)  K+ (g) + e- (g)
I.E. = + 418 kJ
Cl (g) + e- (g)  Cl- (g)
E.A. = - 349 kJ
---------------------------------------K (g) + Cl (g)  K+ (g) + Cl- (g)
∆H = + 69 kJ
Stap III: Vorming van 1 mol ionenpaar in de gasfase:
K+ (g) + Cl- (g)  KCl (g)
∆H = - 443 kJ
Globaal (Stap II + III):
K (g) + Cl (g)  KCl (g)
∆H(berekend) = - 374 kJ
Stap IV: Roosterenergie:
K+ (g) + Cl- (g)  KCl (s)
∆H = - 717 kJ/mol
 K (s) + 1/2 Cl2 (g)  KCl (s) ∆Hf = - 437 kJ/mol
= de vormingswarmte
Edelgasconfiguratrie: 8 elektronen op de buitenste schil die zorgen voor een grote stabiliteit (vb. Na+)
Pseudo – edelgasconfiguratie: ionen met een complete d-schil (vb. Cu+)
Covalente binding (= elektronenpaarbinding)
•
•
•
1 of meer elektronenparen worden gemeenschappelijk genomen,
Atomen streven hierbij naar een octetstructuur.
In een aantal gevallen komt een eenzaam elektonenpaar voor  neemt niet deel aan de reactie.
Enkelvoudige binding:
H2 O
H–O–H
Meervoudige binding:
CO
Resonantie of mesomerie
Het blijkt dat men (uitgaande van de Lewisstructuur) soms twee of meer mogelijkheden heeft
Om de e-paren te verdelen over de atomen of de polyatomische anionen.
SO2
ligt tussen:
O
S
O
of
O
S
O
Radicale moleculen: het voorkomen van ongepaarde elektronen (paramagnetisch) in de molecule
 zeer reactief
Polaire bindingen
Bindingen waarin elektronen asymmetrisch verdeeld zijn voor bindende atomen
 de vorm van de molecule speelt een rol (bij meer als 1 polaire binding)
 vb: H(δ+) – Cl (δ-)
 ∆EN ≠ 0 = klein
Apolaire bindingen
Moleculen met apolaire covalente bindingen.
 vb: H – H
 ∆EN = 0
Dipolaire moleculen
Moleculen met polaire covalente bindingen
 binding geeft het ontstaan aan een elektrisch dipool
 µ (elektrisch dipoolmoment) ≈ ∆EN
Bindingsparameters

Bindingsenergie (B.E.):
o B.E. is de energie-(enthalpie)verandering die optreedt bij het breken, in de gasfase, van
één mol bindingen ter vorming van atomen
o De bindingsenergie is altijd endotherm.
o BE laat ons toe reactiewarmtes en/of vormingswarmtes te berekenen.
o Vb. H2 (g)  2 H (g) B.E. = ∆H = + 436 kJ

Bindingslengte
o Verband tussen de bindingsenergie (B.E.) en de bindingslengte.
 Hoe korter de binding, hoe sterker de binding  hogere B.E..
Verband ionische en covalente binding


De ionische en covalente binding zijn ideale modellen
Geen enkele binding is zuiver ionisch of covalent.
Deze figuur geeft het verband tussen het ionisch karakter van de binding (uitgedrukt in %) en ∆E.N.
van de atomen.
Covalent apolair
Covalent polair
Polair ionisch
(vb. H – H)
(vb. HCl)
(vb. NaCl)
 indeling in apolaire en polaire covalente binding en ionische binding is gedeeltelijk arbitrair
5) De vorm en polariteit van moleculen
De vorm.
De vorm van de moleculen wordt bepaald door de positie van de valentieschil elektronenparen die al
dan niet deelnemen aan de bindingen.
VSEPR: Valentie Schil Elektronen Paar Repulsie principe.
Configuratie waarin de 4 e-paren van een octet zo ver mogelijk uit elkaar liggen  tetraëder
In 3D:
Vb: CH4
 Apolair
Vb: NH3
 Polair
De polariteit.
De polariteit van de moleculen wordt bepaald door de vorm van de moleculen en de polariteit van de
binding  de polariteit van de binding volgt uit de EN
Polaire bindingen
Bindingen waarin elektronen asymmetrisch verdeeld zijn voor bindende atomen
 de vorm van de molecule speelt een rol (bij meer als 1 polaire binding)
 vb: H(δ+) – Cl (δ-)
 ∆EN ≠ 0 = klein
Apolaire bindingen
Moleculen met apolaire covalente bindingen.
 vb: H – H
 ∆EN = 0
De polariteit van moleculen met één binding wordt bepaald door ∆E.N. van de twee atomen
o Vb
NaCl 
EN = 2 polair
H–H 
En = 0 polair

De polariteit van moleculen met meerdere bindingen wordt bepaald door de VORM van het
molecule en de vectoriële som van de polariteiten van de bindingen.
o Onevenwicht 
polair
o Evenwicht

apolair
Vb:

CH4
NH3


4 apolaire bindingen  apolair
vrij e-paar
 polair
De diëlectrische constante
 hangt op een zeer complexe wijze samen met het dipoolmoment (en dus de polariteit) van
moleculen in de vloeistoffase.
 Maat voor de invloed van het oplosmiddel op de electrische aantrekking tussen ionen met
tegengestelde ladingen
 Vb: H2O heeft een uitzonderlijk sterke polariteit.
6) De krachten tussen atomen, ionen en moleculen in vaste stoffen en vloeistoffen.


De aggregatietoestand van de stoffen wordt bepaald door de intermoleculaire krachten.
De krachten tussen atomen, moleculen en ionen bepalen de fysische eigenschappen van
vloeistoffen en de structuur van vaste stoffen.
De aggregatietoestanden van de materie zijn in verband te brengen met twee tegengestelde
effecten: de beweging van de moleculen en de energieveranderingen.
 Voor gassen geldt:
1/2 mv² >> ∆E (gassen)
 Voor vaste stoffen geldt:
1/2 mv² << ∆E (vaste toestand)
 Voor vloeistoffen geldt:
1/2 mv² ≈ ∆E (vloeistoffen).
We bespreken de krachten tussen atomen, ionen en moleculen aan de hand van de
interactieenergieën (potentiële energie) tussen deze deeltjes. De sterkte van de interactie bepaalt
uiteindelijk of een stof bij normale omstandigheden een gas, een vloeistof of een vaste stof is.


Ion-ion interactie (Coulomb)
Energie ≈ (Za x Zb )/d
Z = lading van ion
d = afstand tussen zwaartepunten van de ionen (bepaald smpt)
Door de sterke interactiekrachten, zijn alle ionische verbindingen vaste stoffen met zeer hoog smpt
Vb: Smeltpunt NaCl = 801 °C
Algemeen:
Energie ≈ (Za x Zb)/Dd
D = diëlectrische constante
 Maat voor de invloed van het oplosmiddel op de electrische aantrekking tussen ionen met
tegengestelde ladingen
 vb: Na+ClIon-dipool interactie
Energie ≈ Za x µb /d² µ ≈ ∆E.N
M = dipoolmoment ≈ ∆E
d²  moeten nog dichter bij elkaar liggen om elkaar te voelen.
Vb:
Na < K
E (Na+, H2O) = 2E (K+,H2O)
 Interactie energie
Dipool-dipool interactie

spelen een grote rol bij het bepalen van fysische eigenschappen (oa Kpt) van polaire organische
moleculen
In vaste toestand:
In vloeistof of gas
Vb:
Energie ≈ µa x µb /d3
Energie ≈ µa²x µb² /d6
µ van HCl > µ van HBr
E (HCl, HCl) = 3E (HBr, HBr)
Dispersiekrachten.
Energie ≈ (αa x αb) /d6


α is de polariseerbaarheid van het molecule; een maat voor de
verschuifbaarheid van de elektronen in de moleculen.
London krachten, van der Waals krachten.
Apolaire moleculen zoals H2, N2, O2, Cl2, etc. vertonen een geïnduceerd (door naburen)
dipoolmoment of niet permanent dipoolmoment.
Rol van vorm en massa in de polariseerbaarheid van moleculen.
Vorm
C5
Pentaan: ze kunnen over een grotere afstand bewegen  interactie neemt toe  Kpt stijgt  36°C
Neopentaan : kleinere afstand  kleiner interactie  kleiner kookpunt  10°C
Massa
CH4 (gas)
 CCl4 (vloeistof)
Naast de dipool-dipool interacties er ook moet rekening gehouden worden met dispersiekrachten.
M.a.w. naast het permanent dipool ontstaat er ook een tijdelijk geïnduceerd dipoolmoment.
Waterstofbruggen
Een afwijking van HF, H2O en HI
 Verklaring wordt gezocht in zeer hoge dispersiekrachten
 Waterstofbruggen


Waterstofbruggen komen voor wanneer zich een H-atoom (wegens ∆E.N.: H+) bevindt tussen
de sterk elektronegatieve elementen (F, O, N,…)
Vermindering van H-bruggen bij verhoging van de temperatuur
Consequenties voor water:
1. Kpt stijgt bij H-bruggen en Smpt daalt bij H-bruggen van
 Hoe meer H-bruggen hoe sterker
2. Hogere warmtecapaciteit van H2O
3. Hoge verdampingsenthalpie
 Vermindering van H-bruggen bij verhoging van de temperatuur
4. Groter volume van ijs tov vloeibaar water
 Ijs heeft het maximaal aantal waterstofbruggen
5. V an der Waals constanten in gaswet
 Krachen zijn zo sterk dat H2O molecule aan elkaar blijven hangen.
7) Het fysisch gedrag van vloeistoffen en het fase diagram van water
Viscositeit: weerstand tegen vloeien. (vgl.glycerol met water).
 Hoge viscositeit: sterke intermoleculaire krachten
Oppervlakte spanning
Hydrofiel
Hydrofoob (Cohesiekrachten > adhesiekrachten)
Fysisch evenwicht vloeistof-damp
Het evenwicht vloeistof damp is een DYNAMISCH evenwicht.
 Snelheid van verdamping = snelheid van condensatie
T en P zijn constant
Er gaan een aantal deeltjes van vloeibaar naar gas en omgekeerd, maar
Macroscopisch gebeurt er niets.
Toename van de dampspanning met stijgende T
Verklaring: verdeling van de E over de molecules volgens Maxwell – Boltzmann
Deze worden aangetrokken door vloeistof
Dampspanning en verdampingswarmte.


Als de T stijgt, stijgt de dampspanning
p = po exp (-ΔHverdamping /RT)
Co-existentielijn  evenwicht tussen vloeistof en gas
Kookpunt  als de dampspanning gelijk is aan de atmosferische druk.
Kookpunt daalt als de druk daalt.
Fasediagram van water.
Triple punt: 4,6 Torr; 0,01 °C: drie fasen komen voor in evenwicht
Coëxistentie lijnen: voorwaarde van p en T waar twee fasen samen bestaan (dynamisch evenwicht).
Zeer lage druk : Vast  Damp
Zeer hoge druk : Vast  Vloeibaar
8) De oplosbaarheid van stoffen in vloeistoffen
•
•
De oplosbaarheid van stoffen in oplosmiddelen wordt bepaald door de intermoleculaire
krachten.
De colligatieve eigenschappen van homogene oplossingen wordt verklaard door de
dampdrukverlaging van het solvent die de opgeloste stof uitoefent.
Verzadigde oplossing: dynamisch evenwicht tussen vaste stof en stof in oplossing.
Oplosbaarheid: de concentratie van opgeloste stof in een verzadigde oplossing.
 in functie van het oplosmiddel, temperatuur en bij gassen ook van de druk.
Algemeen principe: Goede oplosbaarheid bij gelijke intermoleculaire krachten.
Vloeistof-vloeistof
•
•
•
Polaire moleculen zijn onderling goed oplosbaar
Vb: C2H5OH (ethanol) en H2O
 H-bruggen
Apolaire moleculen zijn onderling goed oplosbaar
Vb: CCl4 en C6H6 (benzeen)
 Dispersiekrachten
Apolaire moleculen lossen niet op in polaire solventen (oplosmiddel)
Vb: C6H6 en H2O
Vaste stof-vloeistof
•
Ionische vaste stoffen:
Oplosbaar wanneer interactie solvent-ion het haalt van de interactie ion-ion
Vb. Na+Cl-  oplosbaar
Ca++CO3--  onoplosbaar
•
Moleculaire vaste stoffen:
Hoe hoger het smeltpunt van de vaste stof, hoe minder oplosbaar
Als de dispersiekrachten (Vander Waals) groot zijn is het minder goed oplosbaar.
Vb. Br2 (vl) lost beter op in CCl4 dan I2 (v)
•
Relatieve oplosbaarheid:
Apolaire stoffen zijn weinig in water oplosbaar doch goed oplosbaar in apolaire stoffen
(vb: biologische membranen, vetlagen van mens en dier)  DDT
Dit kan kwantitatief worden aangegeven met het verdelingscoëfficiënt K
 De verdeling tussen de olie/water fase is een DYNAMISCH evenwicht.
K = Concentratie in oliefase
Concentratie in waterfase
Polair  K is klein
Apolair  K is groot
Gas-vloeistof
•
•
•
•
De oplosbaarheid van gassen in vloeistoffen is zeer klein  Kleien intermoleculaire krachten
De gassen zijn apolair en bijgevolg beter oplosbaar in benzeen dan in water
De oplosbaarheid van gassen is hoger wanneer het kookpunt van het gas hoger is.
Vb: Xe lost beter op in Benzeen dan He (Xe heeft een hoger kookpunt)
Kookpunt staat in verband met intermoleculaire krachten
 oplosbaarheid houdt verband met intermoleculaire krachten.
Invloed van de temperatuur
•
Over het algemeen lossen vaste stoffen (bv. suikers) beter op bij hogere T (gassen niet)
 bij verhoging van de temperatuur van het oplosmiddel zal het temperatuurverschil tot het
Kpt van het gas groter wordt.
Invloed van druk
Wet van Henry
CA = kH pA
CA = concentratie van gas in oplossing (mM)
pA = partiële druk van het gas boven de oplossing (atm)
kH = Henryconstante is funktie van solvent, opgeloste stof en temperatuur
Vb: op sommige diepten gebruiken duikers He ipv N2 (minder oplosbaar)
Le Chatelier principe:
Een dynamisch evenwicht verzet zich tegen een verandering van de voorwaarden die het evenwicht
bepalen, door het effect van die verandering te minimaliseren.
Bij toename van pA gaat het evenwicht zich aanpassen door de verhoging van CA tot zich een
nieuwe evenwichtstoestand instelt. Bij afname van de druk zal de hoeveelheid opgelost gas dalen.
Colligatieve eigenschappen
 eigenschappen die samenhangen (colligare) met het AANTAL opgeloste deeltjes en NIET met de
chemische AARD van die deeltjes.
Dampdrukverlaging
De verlaging van de dampspanning van het solvent (bv. water) heeft als gevolg:
•
•
Kookpuntsverhoging v/d oplossing
Vriespunstverlaging v/d oplossing
Osmotische druk
Osmose:
Solventstroom naar de geconcentreerde oplossing door een semi-permeable wand die twee oplossingen
scheidt met verschillende concentratie aan opgeloste stof
Osmotische druk (Π)
Druk die nodig is om osmose tegen te gaan
Π = nRT/V
Van ’t Hoff voerde een veranderlijke, i, in:
Π = i . nRT/V
 i houdt rekening met het aantal deeltjes
Illustratie: Gedrag van rode bloedcellen in hypotonische, hypertonische en isotonische vloeistof



Isotonisch: osmotische druk buitenkant = osmotische druk binnenkant
o RBC behouden hun vorm
Hypotonisch: solvent stroomt naar binnen
o Uiteindelijk zal de RBC barsten (vb: in H2O)
Hypetonisch: solvent stroomt naar buiten
o De RBC zullen verschrompelen (vb: in suiker)
Dialyse: hierbij wordt gebruik gemaakt van semi-permeabele membranen om selectief kleine
van grote moleculen te scheiden
9) De snelheid van chemische reacties en de factoren die ze beïnvloeden.
Chemische reacties verlopen met een bepaalde snelheid. De snelheid is functie van de concentratie van
de reagentia, de temperatuur en van een eventueel aanwezige katalysator.
Reactiesnelheid en snelheidsconstante.
AB
v = afstand / tijd
v = snelheid van de reactie: verandering van de concentratie in een bepaald tijdsinterval.
Vb: 2 HI (g)  H2 (g) + I2 (g)
 Na 100 s is HI verminderd met 0,5 mol/L.
Overgang van gemiddelde snelheid naar ogenblikkelijke snelheid
De ogenblikkelijke snelheid is afhankelijk van de tijd
 We zoeken een tijdsonafhankelijke beschrijving van de reactiesnelheid
Twee mogelijke benaderingen:
Snelheid op verschillende tijdstippen
In beide gevallen vindt men : v = k [A]a
Vb:
2 NO2 (g)

Beginsnelheid bij verschillende beginconcentraties
k = sneheidsconstante (enkel afhankelijk vd T)
a = orde van de reactie
2 NO (g) + O2 (g)
experimenteel: v = k [NO2]²

 experimenteel: v = k [NO2]² [CO] 0
Algemeen: v = k [reagens]a
Vb:
NO2 (g) + CO (g)
NO (g) + CO2 (g)
onafhankelijk van de CO-concentratie
Reacties van de eerste orde
A → produkten

v = k [A]o = - d[A]/dt
- d[A]/[A]o = k dt
Integreren tussen de grenzen t en to (begin) waarbij geldt [A] en [A]0, geeft:

[A] = [A]0 exp(-kt) (exponentieel verval)
Bij t = 0 → [A] = [A]0
Bij t = ∞ → [A] = 0
Bepalen van k: ln [A] = ln [A]0 - kt
Halfwaardetijd. (t ½ )
tijd waarbij [A] = [A]0/2
ln[A]0/[A] = k t

ln [A]0/([A]0/2) = k t1/2

Reactie waarbij de t ½ constant is
 reactie van de eerste orde.
T ½ is onafhankelijk van [A] of [A]o
t ½ = constante
Vb: radioactief verval; verdwijnen van geneesmiddelen uit bloed.
Invloed van temperatuur en katalysator
•
•
De snelheid van een chemische reactie kan beïnvloed worden door de concentratie van de
reagentia, de temperatuur en een katalysator.
Temperatuur en katalysator veranderen de snelheid van een reactie door hun invloed op de
snelheidsconstante (k)
Temperatuur
Experimenteel:
k = Ao exp(-Ea/RT)
(Ea = activeringsenergie)
Reacties versnellen bij een hoge T ( meer moleculen hebben de neiging om te reageren)
 vb: koelkast.
Katalysator.
Chemische stof die
- de reactie versnelt
- deelneemt aan de reactie.
- ongewijzigd uit de reactie komt.
- Ea verlaagt
- geen invloed heeft op ∆H.
Homogene katalyse:
Katalysator heeft dezelfde fase als reagentia en produkten.
Bv. [H+] in de reactie van sucrose.
Heterogene katalyse:
Katalysator heeft een andere fase dan de reagentia en de produkten.
Bv. Pt in de HI reactie.
De enzymatische katalyse is een belangrijke vorm van heterogene katalyse
Interpretatie van Maxwell – Boltzmann
Activeringsenergie
Minimum energie die moleculen moeten hebben om te kunnen reageren.
De moleculen verkrijgen die energie door botsingen aan hoge snelheden
Botsingstheorie
= Fysische betekenis van Ea
A (g) + B (g) 
produkten
v (wegens botsingen) = Constante [A][B]
 k (snelheidsconstante) indien alle botsingen leiden tot chemische reactie.
Bijkomende voorwaarden voor reactie van twee botsende moleculen:
• goede oriëntatie (p)
• voldoende energie (f).
v = f . p . Const [A][B]
k = f . p . Const
 fractie van de moleculen die voldoende E hebben
 fractie van de moleculen die een goede oriëntatie hebben
ln f = - Emin/RT
of
ln k = ln (f . p . Constante)
ln k = ln (p . Constante) + ln f
ln k = ln (p . Constante) – (Emin)/RT
ln k = ln Ao – (Ea)/RT
 invloed van T en katalysator.
f = exp (-Emin/RT)
10) Het chemisch evenwicht en de factoren die het beïnvloeden
Fysische en chemische processen evolueren naar een toestand van dynamisch evenwicht. Deze toestand
wordt beschreven door de evenwichtsconstante. Deze verandert onder invloed van de temperatuur.
Chemisch evenwicht.
Vb.
H2 (g) + I2 (g)

2 HI (g)
Experimenteel vinden we dat:
Van R  P: v
=
k [H2][I2]

Van P  R: v
=
k [HI]²
Bij evenwicht geldt: ve = ve
(ve is de snelheid bij evenwicht!)
Dus 
k [H2]e [I2]e
=
k [HI]²e
Macroscopisch veradert er niets, de concentraties blijven dus hetzelfde, maar microscopisch verandert
er wel iets.
(k = reactieconstante en Kc = evenwichtsconstante)
Evenwichtsconstante.
aA + bB → cC + dD

[]  evenwichtsconcentraties
Kc geeft informatie over de concentraties van produkten en reagentia bij evenwicht. Kc geeft geen
informatie over de snelheid waarmee het evenwicht bereikt wordt.
( ) geven NIET – evenwichtsconcentraties aan
Qc = reactiequotiënt
 verhouding van de concentraties van produkten en reagentia bij het begin van
de reactie (niet bij evenwicht)
Qc > Kc
Qc < Kc
Qc = Kc



vorming van reagentia
vorming van produkten
evenwicht
Heterogene evenwichten.
 evenwichten waarbij verschillende fasen voorkomen.
Vb.
CaCO3 (v)

Ca++(aq) + CO3- -(aq)
 K = [Ca (aq)]++ . [CO3 (aq)]-[CaCO3]
(constante/constante)
 Kop = oplosbaarheidprodukt (is een evenwichtsconstante) = [Ca++][CO3- -]
Ook dampspanning H2O is een evenwichtsconstante
Vb.
H2O (vl)

H2O (g)
 K = [H2O]g / [H2O]vl
 is een constante
 K’ = [H2O]g
 omzetten naar dampspanning
Evenwichtsconcentratie in de gasfase: n/V = [H2O]g = patm / RT
 bij gegeven T : K’’ = p H2O
 p = dampspanning
 bij 100°C en 1 atm
(K’’= K’ . RT)
Combinatie van reacties (vgl met wet van Hess)
N2 + 2 O2

2 NO2 (1)
N2 O4

N2 + 2 O2 (2)
------------------------------------------N2 O4

2 NO2 (3)
Hoeveelheid reactieproducten > reagentia
Hoeveelheid reagentia < reactieproducten
 Kc3 = Kc1 . Kc2
 evenwicht nr rechts
 evenwicht nr links
Invloeden op het fysische en chemische evenwicht
Een dynamisch evenwicht “antwoordt” op een verandering in de parameters die het evenwicht bepalen,
door het effect van die veranderingen te minimaliseren
Toevoegen/wegnemen van reagentia/produkten


Kc is constant
Evenwichtsligging verandert; verschuift naar links of rechts, al naargelang wat men
Toevoegt of wegneemt.
Invloed van de druk (gasreacties)



Kc is constant
Evenwichtsligging zal naargelang het type van reactie al dan niet
veranderen.
p↑ dan: R  p
p↓ dan: R  p
Invloed van temperatuur
Experimenteel blijkt dat Kc verandert met de temperatuur.
- Bij endotherme reacties stijgt Kc met stijgende T.
bv: verandering van de dampspanning van water met de temperatuur
- Bij exotherme reacties daalt Kc met stijgende T
bv: de synthesereactie van HI.
Kc = Constante exp(-∆Hreactie/RT)
ln Kc = ln Constante - ∆Hreactie/RT
Invloed van katalysator.
Geen invloed


Een katalysator verlegt het evenwicht niet, het versnelt alleen de reactie
Het verandert alleen activeringsenergie.
11) Zuren, basen en buffers in water
Zuren en basen: definities.
!! Zuren en basen zijn enkel gedefinieerd als ze in water zijn opgelost !!
 NaOH is geen base en HCl is geen zuur!!
Definitie
Zuur = protondonor (geeft in H2O H+)
Base = protonacceptor (geeft in H2O OH-)
Zuur(1) + Base(2) → Zuur(2) + Base(1)
Vb:
HCl (g) + H2O
NH3(g) + H2O


H3O+ + ClNH4+ + OH-


H 3 O + + ABH+ + OH-
Algemeen:
Zuur: HA aq + H2O
Base: B aq + H2O
Evenwicht van zuur en base
H2O kan zowel als zuur als als base kan reageren
H2 O + H 2 O

H3O+ + OH-
(Kc is een constante)
Kw
=
Kw = 10-14

=
Bij 25°C
(experimenteel)
pKw = 14
Evenwicht van zuur:
HA + H2O
[H3O+][OH-]
Kc [H2O]²

A- + H3 O+
In verdunde oplossing:
(Z + B  Z + B)
(B + Z  Z + B)
Evenwicht van base:
B + H2 O
OH- + BH+

 verband tussen Kz en Kb van geconjugeerde paren

HCl (g) + H2O
Kz = [Cl-] [H3O+]
[HCl]
Cl- + H2O
H3O+ + Cl=

Cl + OH-
Kb = [HCl] [OH-]
[Cl-]
=
Kw = Kz. Kb =
=
(Z + B  Z + B)
[B1] . [H3O+]
[Z1]
(B + Z  Z + B)
[Z1] . [OH-]
[B1]
[Cl-] [H3O+] . [HCl] [OH-]
[Cl-] . [HCl]
[H3O+] . [OH-]
Kw = Kz. Kb = 1014
pKw = pKz. pKb = 14
Sterke/zwakke zuren/basen, pH.
Sterke zuren:
Sterke basen:
Zwakke zuren:
Zwakke basen:
Kz >> 1
Kb >> 1
Kz << 1
Kb << 1
Vb: HCl
Vb: NaOH
Vb: CH3COOH
Vb: NH3
Experimentele bepaling van sterkte van zuren en basen:
1. Geleidbaarheid in H2O
2. Osmotische druk
3. pH meten met pH indicator of pH meter
pH = - log10[H3O+]
pH > 7
pH < 7


Base
Zuur
(pH bloed is + 10-7)
Polyprotische zuren
 Zuren die meer dan één proton kunnen afgeven.
Vb: H2CO3 in bloed:
H2CO3 + H2O
-
HCO3 + H2O
⇄
HCO3- + H3O+
⇄
--
CO3 + H3O
pKz1 > pKz2
+
De vgl. van Henderson - Hasselbalch
HA ⇄
A- + H+

Zouten in water
Zuur + base → zout + H2O
•
Sterke base + sterk zuur
o
Vb:



neutraal
NaCl + H2O 
Na+ (aq) + Cl- (aq)
Na+ + OHCl- + H+
NaOH
HCl


! Idem voor zwak zuur en zwakke base !
•
Zwak zuur + sterke base
o Vb:


•


licht basisch

CH3COOH + NaOH
Na+ + OHCH3COO- + H+
Sterk zuur + zwakke base
o Vb:

HCl + NH3


NaOH
CH3COOH

licht zuur

NH4Cl
NH4+ + OH- 
Cl- + H+

CH3COONa + H2O
NH3 + H2O
HCl
Buffermengsels in bloed en cellen (BELANGRIJK!!!)
Buffer: Oplossing van zwak zuur/base met zijn geconjugeerde base/zuur die de veranderingen in pH
beperkt bij toevoegen van zuur of base.
Bij toevoegen van 10-2 mol HCl aan 1 liter H2O: pH 7 → pH = 2.
Bij toevoegen van zelfde hoeveelheid HCl aan 1 liter bloed: pH 7,4 → pH 7,35.
In het bloed is blijkbaar een stof aanwezig die de pH van het bloed “buffert” bij het toevoegen ve zuur.
In het bloed: H2CO3/HCO3- (naast proteïnen)
Reacties die de bufferende werking verklaren in het bloed:
•
•
Toevoegen van base:
Toevoegen van zuur:
H2CO3 - + OH
HCO3- + H3O+


H2O + HCO3 –
H2CO3 + H2O.
Vermits [HCO3-] = 20 [H2CO3] buffert het bloed beter tegen zuur (melkzuur) dan tegen base.
pH bloed 7,4
bij coma 7,0
bij tetanus 7,8
oceaan 8,4
12) De entropie, de vrije energie en hun verband met het chemisch evenwicht
•
•
De richting waarin fysische en chemische processen spontaan evolueren wordt bepaald door de
totale entropieverandering die optreedt in het proces.
De verandering in vrije energie van een proces kan berekend worden met de vormings vrije
energie van de verbindingen die deelnemen aan de reactie. Onder bepaalde voorwaarden is de
verandering in vrije energie verbonden met de evenwichtsconstante.
Tendens van fysische en chemische processen
Fysische en chemische processen evolueren naar een evenwichtstoestand.

Een aantal processen, vooral chemische kunnen zeer traag verlopen.
 In het vervolg wordt dan ook alleen een uitspraak gedaan over de
mogelijkheid van een proces, niet over de snelheid waarmee het optreedt.
Spontane en niet spontane processen
Fysische processen
Voorbeelden van spontane processen:
Expansie van gassen
Verdampen van vloeistoffen
Mengen van vloeistoffen
∆H = 0
∆H = +
∆H = 0
( gas1 + gas2  mengsel)
(H2O (vl)  H2O (g))
mengen spontaan
 omgekeerde processen zijn niet spontaan maar wel mogelijk door toevoegen van E
Eerste wet van thermodynamica:
Behoud van energie en materie in een geïsoleerd systeem
 Zegt niets over de tendens van processen.
 ∆H is geen criterium voor het spontaan karakter van deze processen.
Tweede wet van thermodynamica:
Energie en materie hebben een neiging zich te spreiden over een zo groot mogelijke ruimte.
 entropie is een maat voor wanorde
 natuurlijke processen evolueren in de richting van orde naar wanorde
 Zegt niets over de snelheid.
Chemische processen
Vb:
CH4 + 2 O2
C6H12O6 + 6 O2


CO2 + 2 H2O
6CO2 + 6 H2O
verbrandingen
ademhaling
Aantal spontane processen (vooral chemische reacties) verlopen zeer traag
 Tweede wet zegt niets over de snelheid van de processen!
 Het omgekeerde proces van de ademhaling, de fotosynthese, is niet spontaan en
verloopt dus enkel bij de toevoer van (zonne) energie
Entropie
 De graad van wanorde van een systeem (of zijn omgeving)
S = k ln W
k = R/N = Boltzmannconstante
W = aantal plaatsingsmogelijkheden bij spreiding van materie
S = energie/T = J/K =


toestandsfunctie
Invloed van de aggregatietoestand en de complexiteit (aantal atomen) van de moleculen.
 S gas > S vloeistof > S vast
De absolute waarde van de molaire entropie kan experimenteel bepaald worden uit de
temperatuursafhankelijkheid van de molaire warmtecapaciteit.
Fysische processen
Expansie van een gas
N moleculen: W= 2N plaatsingsmogelijkheden
∆S
= S2 - S1
= k ln 2N - k ln 1 N
= k N (ln2 – ln 1)
= R ln2 = 576 J/k.mol
Smelten van ijs (bij 0 °C)
∆S(reactie) = S(produkten) - S(reagentia)
H2O (v)

H2O (vl)
∆S(reactie) = S(vl) - S(v) = 22 J/Kmol
Bij fysische reactie: spontane reacties gaan gepaard met een positieve ∆S van het systeem.
Chemische reacties
Vb.
H2 (g) + 1/2 O2 (g)

H2O (vl)
∆S(reactie) = SH2O (vl) – SH2 (g) – S1/2 O2 (g) = - 162 J/K.mol H2
∆S = negatief in dit spontaan proces
 de tegenstrijdigheid van de tweede wet is slechts schijnbaar want de verandering van
de entropie in de omgeving werd niet in rekening genomen. (enkel ∆S in reactievat)
∆S(omgeving) = - ∆H(reactie)/T
(reactie = systeem)
∆S(totaal) = ∆S(reactie) + ∆S(omgeving)  is altijd positief
 Een spontane verandering gaat gepaard met een toename van de TOTALE entropie.
∆S(totaal) > 0
Vrije energie: verband reactiewarmte en reactieëntropie
∆S(totaal) = ∆S(reactie) + ∆S(omgeving)
∆S(totaal) = ∆S(reactie) - ∆H(reactie)/T
 -T.∆S(totaal) = -T.∆S(reactie) + ∆H(reactie)
Definitie van de Gibbs vrije energie of chemische potentiaal:
∆G(reactie)
= - T ∆S(totaal)
= -T.∆S(reactie) + ∆H(reactie)
∆G:
mogelijkheid van een reactie om arbeid te leveren, de energie die beschikbaar (vrije energie) is
om arbeid te leveren bij constante druk.
G:
chemische potentiaal van een stof: de potentiaal (mogelijkheid, bereidheid) van een zuivere stof
om een chemische reactie te ondergaan met een andere stof of om te diffunderen van een plaats
naar een andere plaats in een systeem (fysische omzetting).
∆G = ∆H - T∆S
Spontaan:
Niet spontaan:
Evenwicht:
Vb.
∆S(totaal)
∆S(totaal)
∆S(totaal)
C6H12O6 (s) + 6 O2 (g)
∆H = ∆S = +
∆G = -



=
=
=
+
0
∆G(reactie)
∆G(reactie)
∆G(reactie)
=
=
=

6 CO2 (g) + 6 H2O (vl)
exotherm
wanorde stijgt
exergonisch  spontaan
Koppeling van endergonische en exergonische reactie
Endergonische processen
Vb:
Mechanische arbeid: spierarbeid
Exergonische processen
Vb: Ademhaling: verbranding van suikers, vetten, etc.
Koppeling van endergonische en exergonische reacties is mogelijk.
+
0
(exergonisch proces)
(endergonisch proces)
Vrije energie: verband met chemisch evenwicht
∆G = - RT ln (K/Q)
K = evenwichtsconstante
Q = reactiequotient
Tendens  P:
Tendens  R:
Evenwicht:
Q<K
Q>K
Q=K
Met Q = 1
(P en R: 1 mol/L, 25 °C, 1 atm)
∆G° = - RT ln K
(∆G° is ∆G onder standaardvoorwaarden)
∆S(totaal) > 0
∆S(totaal) < 0
∆S(totaal) = 0
∆G(reactie) = ∆G(reactie) = +
∆G(reactie) = 0
of ∆G° = - RT 2,303 log K
Deze uitdrukking laat toe K te berekenen
∆G = ∆G° + RT ln Q
13) De Nernstvergelijking en zijn verband met het chemisch evenwicht
De vergelijking van Nerts geeft het verband tussen de elektrische spanning die een reactie kan leveren
en de verandering van vrije energie.
Een groot aantal chemische reacties kunnen beschouwd worden als processen waarbij elektronen
worden overgedragen van het ene reagens op het andere.
• analogie tussen proton(H+)transfer (zuur-base reacties) en elektron(e-)transfer (oxido-reductie
reacties).
• Beide types van reacties kunnen we opdelen in twee stappen (half-reacties).
Halfreacties.
Protondonor (zuur) = protonacceptor (base) + H+
Elektrondonor (reductans) = elektronacceptor (oxidans) + eo Electrondonor: reduceert een andere stof maar wordt zelf geoxideerd
o Electronacceptor: oxideert een andere stof en wordt zelf gereduceerd.


Vb.
CH3COOH
H2 O + H +
Som:
CH3COOH + H2O
Vb.
Na

½ Cl2 + e-
Som: Na + 1/2 Cl2
CH3COO- + H+
H3 O+
⇄
Protontransfer
CH3COO- + H3O+
Elektronentransfer
Na+ + e
Cl-

Na+Cl-
Toepassing van elektronenoverdracht
 verzilvering van Cu
Cu (v) + 2 Ag+ (aq) 
Cu+ (aq) + 2 Ag (v)
Dompelen we een koperstaaf in een oplossing van een zilverzout, dan bemerken we de vorming van
een neerslag van zilver op het koper.
Zoutbrug vervoert ionen
Metaalgeleidende stroomdraad vervoert e
Cu  Cu2+ aq + 2 e-
/
Ag+ aq + e-  Ag
Het verband tussen de elektrische spanning die een reactie kan geven (bat) en het chemisch evenwicht
∆G = - RT ln (K/Q)
Bij een spontane reactie waarbij elektronen uitgewisseld worden verwachten we een positieve
spanning (E)
∆G = - n F E
n: aantal elektronen dat wordt overgedragen per atoom/ion.
F : Faraday constante
E : spanning
- n F E = - RT ln (K/Q)
(n = 1)
 E = (RT/F) ln (K/Q)
Bij Q = K :
Bij Q = 1:
evenwicht  geen spanning!
E°= (RT/F) lnK
E = E° - (RT/F) lnQ
E = E°- (59 mV/n) log10Q
(bij 25°C)
Toepassingen van Nernst vgl.
- Meten van evenwichtsconstante K via meten van E
- Meten van [H+]: elektrische pH meter
- Communicatie tussen cellen via electrische impulsen
14) De alifatische en aromatische koolwaterstoffen en hun voorkomen in
biomoleculen.
Alifatische KW
Alkanen, alkenen, alkynen. Gewonnen uit aardolie (van biologische oorsprong). Alifatisch: (Grieks)
zalf, olie, vet.
14.1.1.1 Verzadigde KW
15) De alcoholen, aldehyden, ketonen, ethers en koolhydraten en bespreek in het
kort de rol van koolhydraten in de voeding
Functionele groepen die voorkomen in biomoleculen:
Koolhydraten: alcoholen, aldehyden, ketonen, ethers
Lipiden: alcoholen, zuren, esters
Eiwitten: carbonzuren, aminen, aminozuren, amiden
Nucleïnezuren: aromatische aminen, koolhydraten, fosforzuur esters
Koolhydraten, lipiden (vetten) en eiwitten (proteïnen) zijn belangrijke bestanddelen van ons voedsel
naast vitaminen en mineralen.
Alcohol: R-O-H
Vbn: CH3-OH
CH3-CH2-OH
Methanol
Ethanol
Isomerie:
•
Functie-isomerie:
CH3-CH2-OH
of
•
Positie-isomerie:
CH3 CH2 CH2 OH
of
CH3-O-CH3
Fysische Eigenschappen
-
Het kookpunt stijgt als de intermoleculaire krachten stijgen  als het aantal H-bruggen stijgt
o CH3 CH2 OH
↓ stijging kookpunt
o CH3 CHOH CH2 OH
-
De oplosbaarheid in H2O hangt af van de ketenlengte van het alifatische KW
o (hoe langer hoe minder oplosbaar)
R - groep
----------------------- OH
Hydrofoob (onoplosbaar)
Hydrofiel (oplosbaar)
vb: cholesterol
Chemische Eigenschappen
1. Ionisatie: veel zwakker dan H2O
2. Oxidatie en reductie
- bv.: verzuren van wijn onder invloed van Acetobacter bacteriën
o CH3CH2OH + O2

CH3COOH + H2O
- Primaire alcoholen: 
aldehyden

carbonzuren
o CH3-CH2-CH2OH 
R-CHO

R-COOH
- Primaire alcoholen: 
aldehyden

carbonzuren
- Secundaire alcoholen:  ketonen
o CH3-CHOH-CH3

R2CO
3. Estervorming: met organische en anorganische zuren
Alcohol + zuur

Ester + Water
CH3-CH2-O{H + HO}-SO2-OH

CH3-CH2-O-SO2-OH + H2O
Esters: R –O – R
Zeer brandbaar  bewaren in een bruine fles
Alcohol + zuur

Ester + Water
Waarom bewaren in een bruine fles?  tegen het verdampen
R–O–R

+ licht
2RCOOH
Aldehyden en ketonen
Bevatten de polaire C=O binding
Aldehyde:
RHC=O
Belangrijke aldehyden: CH2O (formol) en CH3CHO (acetaldehyde).
Keton
R2C=O
Belangrijk keton: (CH3)2C=O (aceton).
Fysische eigenschappen
o Kookpunt: dipool – dipool interacties voor aldehyden en H – bruggen voor ketonen
o Oplosbaarheid: daalt als de lengte van de KW – keten stijgt
Chemische eigenschappen
1. Oxidatie en reductie
Gevormd uit alcoholen:
CH3OH
C2H5OH


CH2O (formol)
CH3CHO
Oxidatieproducten:
CH2O
CH3CHO


HCOOH
CH3COOH
Reductie:
CH2O

CH3OH


CO2 + H2O
CO2 + H2O
CH3CHO

CH3CH2OH

C6H12O6 glucose
2. Additiereactie op C=O binding
Koolhydraten
Cm(H2O)n
Vb:
m=n=6
Functionele groepen in koolhydraten: alcoholen, aldehyden, ketonen, ethers.
Suikers, zetmeel, glycogeen, …
16) De carbonzuren, aminen, aminozuren, amiden en eiwitten en bespreek in het
kort de rol van eiwitten in de voeding
17) De alcoholen, zuren, esters en lipiden en bespreek in het kort de rol van lipiden
in de voeding