Statistiek A + B: Overzicht voor tentamen
SIG KLEINER DAN ALPHA : H0 VERWERPEN!!!!!!!!
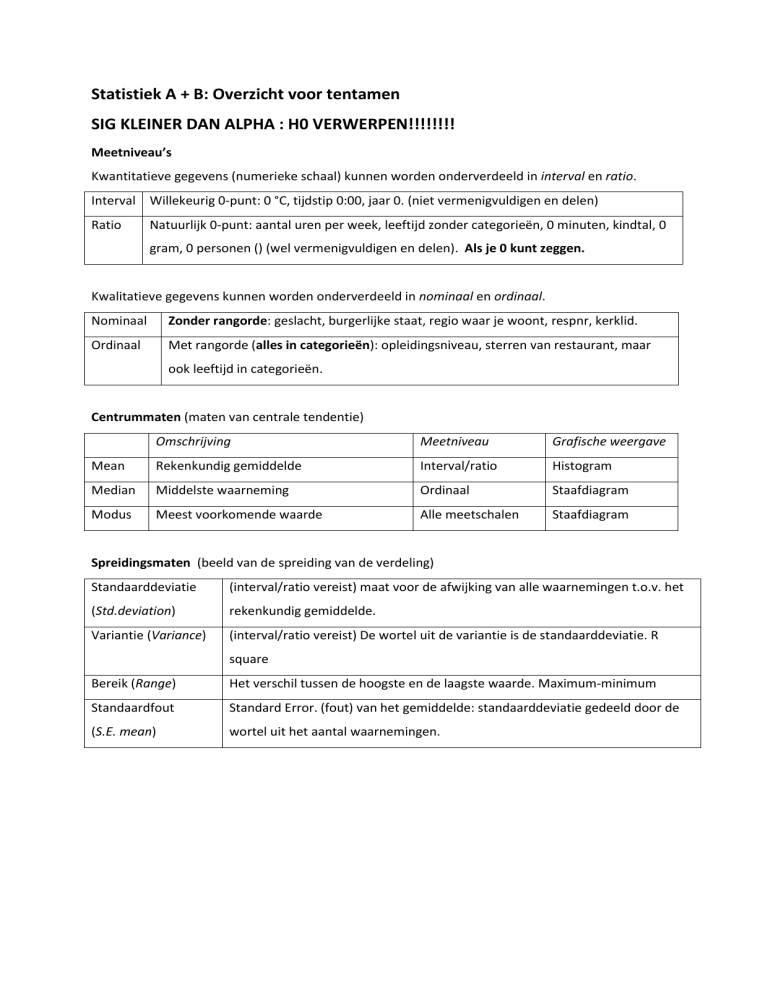
Meetniveau’s
Kwantitatieve gegevens (numerieke schaal) kunnen worden onderverdeeld in interval en ratio.
Interval Willekeurig 0-punt: 0 °C, tijdstip 0:00, jaar 0. (niet vermenigvuldigen en delen)
Ratio
Natuurlijk 0-punt: aantal uren per week, leeftijd zonder categorieën, 0 minuten, kindtal, 0
gram, 0 personen () (wel vermenigvuldigen en delen). Als je 0 kunt zeggen.
Kwalitatieve gegevens kunnen worden onderverdeeld in nominaal en ordinaal.
Nominaal
Zonder rangorde: geslacht, burgerlijke staat, regio waar je woont, respnr, kerklid.
Ordinaal
Met rangorde (alles in categorieën): opleidingsniveau, sterren van restaurant, maar
ook leeftijd in categorieën.
Centrummaten (maten van centrale tendentie)
Omschrijving
Meetniveau
Grafische weergave
Mean
Rekenkundig gemiddelde
Interval/ratio
Histogram
Median
Middelste waarneming
Ordinaal
Staafdiagram
Modus
Meest voorkomende waarde
Alle meetschalen
Staafdiagram
Spreidingsmaten (beeld van de spreiding van de verdeling)
Standaarddeviatie
(interval/ratio vereist) maat voor de afwijking van alle waarnemingen t.o.v. het
(Std.deviation)
rekenkundig gemiddelde.
Variantie (Variance)
(interval/ratio vereist) De wortel uit de variantie is de standaarddeviatie. R
square
Bereik (Range)
Het verschil tussen de hoogste en de laagste waarde. Maximum-minimum
Standaardfout
Standard Error. (fout) van het gemiddelde: standaarddeviatie gedeeld door de
(S.E. mean)
wortel uit het aantal waarnemingen.
Betekenis van de standaarddeviatie (p. 47 McClave)
Empirische
Frequentieverdeling is heuvelvormig
regel
en symmetrisch. (ook skewness!)
Regel van
De vorm van de frequentieverdeling
Tsjebysjev
maakt niet uit.
Z-Score (Standaardiseren van een interval/ratio variabele)
hoeveel eenheden standaarddeviatie een
waarneming boven of onder het gemiddelde ligt.
Z = waarde (X) - rekenkundig gemiddelde (µ)
standaarddeviatie (σ)
x-xgemiddeld/standaardafwijking = z
Boxplot (Spreiding van een verdeling, (p.145 de Vocht, p. 56 McClave)
Een rechthoek (box) met de einden (hinges) ter
hoogte van het eerste en het derde kwartiel (Q1
en Q3). De mediaan wordt meestal met een lijn
aangegeven.
De horizontale strepen/uiteinden (whiskers/inner fences) zijn de hoogst en laagst voorkomende
waarde binnen een afstand van 1,5 IQR tot aan de box. De rondjes (outliers) liggen tussen de 1,5 en
3 IQR en de * op meer dan 3 IQR. (Vaak incorrect of behoort niet tot de populatie.)
IQR = interkwartielafstand = Q3 – Q1 = spreiding in de middelste 50%.
P-waarde (probability-waarde)
Bij elke toets berekent SPSS de overschrijdingskans of significantie (in kolom Sig.) Dit wordt de pwaarde genoemd.
Intervalschatting
Het berekenen van de lower en de upper bound.
- Bij een 90% betrouwbaarheidsinterval dien je de
standaardfout te vermenigvuldigen met 1.65.
- Bij een 95% “ “ “ “ met 1.96
- Bij een 99% “ “ “ “ met 2.58.
Deze trek je af aan de ene zijde (van het
gemiddelde) en aan de andere kant tel je het op.
Het betrouwbaarheidsniveau is een betere indicator voor het vaststellen van de
populatiewaarde van als deze laag is omdat dan beter zichtbaar is waar ergens de komt te
liggen.
Hypothese
Een voorlopig (theoretisch) antwoord op een onderzoeksvraag over 1
kenmerk of de relatie tussen 2 of meer kenmerken in een populatie.
Nul-
Representeert de huidige situatie. Heeft altijd een gelijkheidsteken: =
hypothese
Specificatie: H0: µ = een getal. (Er is geen verschil in…)
Alternatieve- Tegenovergestelde van de nul-hypothese. Heeft altijd een ongelijkheidsteken:
Hypothese
<> (= met een streep erdoor). Ha: µ = < een getal. (…is lager, hoger, niet gelijk
aan…)
Eenzijdig
de score op 1 moment, of de verandering van de score in de tijd.
< = linkszijdig. > = rechtszijdig
Tweezijdig
de relatie tussen variabele op 1 moment, of de veranderingen van de relaties
in de tijd. (= met een streep erdoor.) (Er wordt geen richting aangegeven.)
Alpha
ά (vaak ,01; ,05; ,10)
Type 1 fout
Ten onrechte wordt de nul-hypothese verworpen. Hij is dus juist maar is toch
buiten het betrouwbaarheidsinterval gekomen.
Type 2 fout
De nul-hypothese wordt ten onrechte juist bevonden. Hij valt dus binnen het
betrouwbaarheidsinterval terwijl dat in werkelijkheid niet zo is.
Stappen bij het toetsen van H0
1. Bepaal H0
4. Kies n
7. verzamel data
2. Bepaal HA
5. Kies test
8. bereken toetswaarde
3. Kies ά
6. Bepaal de kritieke waarden
9.Trek en verwoord
(betrouwbaarheidsinterval)
statistische conclusie.
Compare means
-
H0 = Er is geen verschil tussen het landelijk gemiddelde
maatschappijkritiek en de maatschappijkritiek van PvdA stemmers.
One-Sample T
-
H1 = Er is wel verschil “ ” ” ”.
-
H0 = Er is geen verschil tussen het landelijk gemiddelde
Test
maatschappijkritiek en de maatschappijkritiek van SGP stemmers.
-
H1 = SGP –stemmers hebben een lager gemiddelde op de variabele
maatschappijkritiek dan het landelijk gemiddelde.
Independent
-
Samples T test
H0 = Er is geen verschil tussen lager en hoger opgeleiden wat betreft
de traditionele man/vrouw rolopvatting in Suriname in 1992.
-
H1 = Lager opgeleiden hebben een meer traditionele man/vrouw
rolopvatting dan hoger opgeleiden in Suriname in 1992.
Uit het betrouwbaarheidsinterval blijkt dat je voor 95% zeker kunt zijn dat het
het gemiddeld verschil ligt tussen Lower en Upper. De significantie ligt niet in
dit interval, daarom moet de H0 worden verworpen.
Paired-Samples
-
T test
H0 = Er is geen verschil tussen het belang dat mensen hechten aan
economische/burgerlijke- en aan maatschappijkritische waarden.
-
H1 = Er is wel verschil tussen “ “ “ “.
Z-toets (of T)
Kijk of de berekende Z-waarde
binnen de genoemde waarden
valt. Als deze er buiten valt,
moet de nul-hypothese worden
verworpen.
Betrouwbaarheid
ά (alpha)
ά/2
z
0.10
0.05
1.645
1001(1 – ά)
90%
95%
0.05
0.025
1.96
99%
0.01
0.005
2.575
T-toets (Steekproefgemiddelden vergelijken) (al of niet een significant verschil?)
T-waarde
Berekenen (test-variable)
Mean difference/standaardfout
Vrijheids-
‘Degrees of freedom’ De werkelijke hoeveelheid variatie in de
Graden (df)
steekproefverdeling van t hangt af van de steekproefomvang van n. Deze
afhankelijkheid wordt uitgedruk door te zeggen dat de t-verdeling (n - 1)
vrijheidsgraden heeft. (Des te kleiner = variabeler.)
Sig. (2 tailed)
De significantie van de t-waarde.
Kijk of deze significantie onder de alpha
(Overschrijdingskans p) (Bij
blijft. Wanneer dit niet zo is, wordt H0
eenzijdig toetsen delen door 2.)
verworpen.
Mean
Het verschil tussen de het steekproefgemiddelde (x met streep erboven) en
difference
het theoretisch gemiddelde µ0.
Betrouwbaar-
Het interval is het verschil tussen het theoretisch- (Test value) en
heidsinterval
steekproefgemiddelde. Interval geeft aan dat de Mean difference in ?% van de
gevallen tussen de Lower & Upper zal liggen. Het populatiegemiddelde µ ligt
tussen (Test value + Lower) en (Test value + Upper)
Regressie
R
Regressie- of B-coëfficiënt. Dit
Tabel Coëfficiënt; onder constant (de X)
is de hellingshoek van de lijn.
staat de schatting van B-coëfficiënt van
Geeft weer met hoeveel
X.
eenheden Y verandert als X met Bij positief: X neemt toe, Y ook.
Intercept
één eenheid toeneemt.
Bij negatief: X neemt toe, Y neemt af.
Het snijpunt van de lijn met de
Tabel Coëfficiënt; onder
Y-as. De voorspelde waarde van Unstandardized Coefficients; Onder B
Y als X = 0.
en achter Constant; hier staat de
kleinste schatting van het intercept.
SSE
Som van kwadraten van de fouten. (Sum of Square for Error.)
s²
Standard Error of the Estimate
(Steekproefvariantie?)
s = √s
SSE
s² = n – 2
Voor SSE en df: kijk bij
‘Residual’.
Standard Error of the Regression model.
Scatterplot
2 of 3 interval- of ratiovariabelen
Graphs; Scatter/Dot; Simple; Define;
Spreidingsdiagram
tegen elkaar afzetten. Vooral bij
Selecteer variabelen Y Axis; X Axis;
correlatie en regressie om een lineair
Paste; Ok.
verband op te sporen tussen de
variabelen.
Enkelvoudige
Het causale verband tussen X en Y
Analyze; Regression; Linear;
regressie
wordt uitgedrukt in een lineaire
Dependent en Indepedent: vul
regressievergelijking. (Waarden van Y
variabele in; Paste; Ok.
voorspellen aan de hand van X.)
Partiele
Testen Multicollineariteit: correlaties
Correlaties
van r > = 0.9. Zo ja, moet je de beide
variabelen buiten je model houden.
Correlatie
Geeft de sterkte en de richting van een verband tussen twee variabelen
weer.
Pearson’s
Is een maat voor het lineaire verband tussen twee interval/ratio variabelen.
Correlatiecoëfficiënt
(Als er ook sprake is van een derde variabele = partiële correlatie.
Positief verband: X stijgt, Y ook. Negatief verband: X stijgt, Y neemt af.
Eigenschappen
-
de waarde van r ligt altijd tussen -1 en +1.
Pearson
-
Als r = 0 is er geen correlatie tussen beide variabelen.
-
Correlatie tussen X en Y = correlatie Y en X = r is symmetrisch
-
Hoe hoger de absolute waarde van r, des te sterker het verband.
Vooronderstellingen
-
r² (deter.co.)= het aandeel verklaarde variantie van Y door X.
-
het verband is lineair (controleren met een scatterplot)
-
Bivariate normale verdeling.
Tabellen bij (enkelvoudige) regressie
Model Summary
R
Correlatie (coefficient) van X met Y.
R Square
Determinantiecoëfficiënt: geeft het
R square in tabel = .450. 45% van de variantie
(R²)
percentage verklaarde variantie in Y
‘winkelen’ wordt dus verklaard door ‘afstand’.
door X aan;
R square = 1 = perfect model,
R square = 0= geen linear verband.
Std. Error of
Standaarddeviatie van de residuen.
the Estimate
(residuen zijn verschillen tussen de
s²
voorspelde en echte Y-waarden.) Is
SSE
s² = n – 2
Voor SSE en df: kijk bij
‘Residual’.
gelijk aan de wortel uit de variantie
(Mean Square) van de residuen.
ANOVA (variantie-analyse: toetsen of het hele model significant is: als sig: <=0.05.)
Regression en Residual
Verklaarde variantie en onverklaarde variantie
Sum of Squares
Bij Total: totale variatie. Het aandeel verklaarde variantie is wat bij SofS
Kwadraat sommen
achter Regression staat / totaal. Dit komt overeen met R Square.
Df. (vrijheidsgraden)
Het aantal vrijheidsgraden van de residuen (Residual) is gelijk aan het
aantal cases min het aantal onafhankelijke variabelen min 1.
Total – Regression -1 = Residual.
Het aantal df. In Regression is gelijk aan het aantal Y.
Mean square
Variantie. De Sum of Squares gedeeld door df.
F
Toont of het regressiemodel significant is. F = de mean squares op elkaar
delen. (verklaarde op onverklaarde varianties.)
Coefficients (componenten voor regressievergelijking)
B0 (Constant)
Staan beide met St. Error in de kolom Undstandardized Coefficients. De
B1 (Regressiecoëfficiënt)
intercept B0 (linkerbovenhoek!). Bv. winkelen = 7 – 0.5 x afstand. Een
toename van de afstand 1 km. een afname van het aantal bezoekers met
0,5 betekent.
Beta
Bij enkelvoudige regressie gelijk aan R, heeft hier geen verdere betekenis.
T-waarde
Je toetst de nulhypothese dat de B1 gelijk is aan 0. (t-waarde: B/St. Error)
Multipele regressie
Er wordt een lineair regressiemodel gemaakt tussen afhankelijke variabele Y
en meerdere onafhankelijke variabelen (regressors) X.
Veronderstellingen
-
Y = interval/ratio; X = interval/ratio of ordinal
-
Verband tussen Y en X is causaal.
-
Multipele regressie is lineair. (Kun je controleren met residuen.)
-
Geen multicollineariteit.
-
Normale verdeling (met dezelfde variantie) van de Y-waarden.
(Residuen normaal verdeeld en evenwichtig gespreid.)
Regressievergelijking
Voorspelde Y = Bo x X1 + Bo + X1 + Bk x Xk.
Elke onafhankelijke variabele X heeft een eigen B1. (regressiecoëfficiënt.)
Residuen
De verschillen tussen de voorspelde Y-waarden en de ‘echte’ Y-waarden.
Multicollineariteit
Er mogen geen onafhankelijke variabelen in het model zijn, die ongeveer
hetzelfde meten. Dit kun je vooraf controleren door de bivariate correlatiecoëfficiënten van alle paren onafhankelijke variabelen te berekenen.
Multicollineariteit = als er correlaties van r > = 0.9. In dat geval moet je de
beide variabelen buiten je model houden.
Standaard methode
Alle onafhankelijke variabelen, (ook de niet significante) tegelijk in het model
brengen. In één keer berekenen.
Stapsgewijze
Stap voor stap een onafhankelijke variabele in het model opnemen, op
methoden
volgorde van de relatieve invloed op de afhankelijke Y (hoogste F-waarde en
laagste significantie). Dit proces stopt als alle significante X-en zijn verwerkt.
Beta-coefficient
Geeft een indicatie van het relatieve belang van iedere X.
Regressieanalyse
De residuen zijn de verschillen tussen de waargenomen Y-waarden en de
voorspelde Y-waarden.
Residuenanalyse
Hiermee kun je nagaan of aan een aantal vooronderstellingen van regressie (en
correlatie) zijn voldaan. De residuen geven een beeld van de kwaliteit van het
regressiemodel. Hoe dichter de punten bij de lijn liggen, des te kleiner zijn de
residuen en des te sterker is het verband en des te beter is de kwaliteit van het
regressiemodel.
Zijn de residuen
Analyze; Regression; Linear; geen X en Y invullen; Plots; Kies: Histogram en
normaal verdeeld?
Normal probability plot; Continue; Paste; Run.
F – toets (variantie-analyse)
Variantie-analyse
Om te toetsen of populatiegemiddelde van een interval/ratiovariabele
(N>= 30)
voor drie of meer onafhankelijke groepen aan elkaar gelijk zijn. De groepen
worden onderscheiden op basis van categorale variabelen.
Vooronderstellingen
-
Alle steekproeven zijn onafhankelijk en select.
-
Elke groep is afkomstig uit een normaal verdeelde populatie.
-
De varianties van de groepen zijn in de populatie aan elkaar gelijk.
(Levene’s toets.) (als alle groepen ongeveer even groot zijn hoeft
dit niet zo strikt.)
Ho
Ho = µ1 = µ2 = µ3 = µk. Populatiegemiddelden van alle groepen zijn gelijk
F
Toont of het regressiemodel significant is. F = de mean squares op elkaar
delen. (verklaarde op onverklaarde varianties)
F-waarde 1 = gemiddelde van alle groepen aan elkaar gelijk zijn. Ho wordt
dan niet verworpen.
F waarde > 1 = Ho verwerpen. De groepsgemiddelden verschillen
significant. De spreiding is veroorzaakt door verschillen tussen de groepen.
(NB: Met de T-toets, toets je de onafhankelijke Y’s, want niet alle
variabelen hoeven relevant te zijn.)
Variatie
Variantie-analyse is gebaseerd op de variatie in steekproefgegevens.
Variatie = de gekwadrateerde afwijking van alle waarnemingen t.o.v. het
gemiddelde (Sum of Squares) Door de variatie te delen door het aantal
vrijheidsgraden verkrijg je de variantie.
Score buiten de whiskers: score valt 1,5 keer buiten de interkwartielafstand
μ = E: N*P
σ2 = n*p*q
µ+2σ en µ-2σ
Schatting.
µ+3σ en µ-3σ
Schatting
Empirische Regel
Hier binnen valt 95% van de
waarden
Volgens de empirische regel is de
kans dat een behandelde patiënt
hierbinnen .95
Hier binnen valt 99.7% van de
waarden
Volgens de empirische regel is de
kans dat een behandelde patiënt
hierbinnen valt .997
Chebyshev
Hier binnen valt 75% van de
waarden
Volgens de Chebyshev regel is de
kans dat een behandelde patiënt
hierbinnen valt .75
Hier binnen valt 88.9% van de
waarden
Volgens de Chebyshev regel is de
kans dat een behandelde patiënt
hierbinnen valt .889
Statistiek A: welke toets moet je gebruiken?
1. Onderzoeken of er een relatie bestaat tussen variabele A en B
KRUISTABEL (Chi2 en Cramer’s V) SPSS pag. 67
Dit is tevens de enige toets waarbij je ne nulhypothese niet wil verwerpen!
H0: de twee variabelen zijn onafhankelijk
Ha: de twee variabelen zijn afhankelijk
2. Onderzoeken of de waarde van een bepaald steekproefgemiddelde afwijkt van een
van tevoren verwacht theoretisch gemiddelde (µ) onder de nulhypothese
T-TOETS OP ÉÉN GEMIDDELDE (ONE-SAMPLE T-TEST) SPSS pag. 77
H0: µ = …
Ha: µ ≠ …
3. Onderzoeken of de gemiddelden van twee groepen van elkaar afwijken
1) Vergelijking van twee onafhankelijke groepen
INDEPENDENT SAMPLES T-TEST SPSS pag. 80
H0: µ1- µ2 = 0
Ha: µ1- µ2 ≠ 0
2) Vergelijking van twee afhankelijke groepen
PAIRED SAMPLES T-TEST SPSS pag. 83
H0: µD = 0
Ha: µD ≠ 0
4. Onderzoeken of twee kwantitatieve variabelen verband met elkaar houden en kijken
hoe sterk dit verband is
1) één afhankelijke en één onafhankelijke variabele
ENKELVOUDIGE LINEAIRE REGRESSIE ANALYSE SPSS pag. 88
H0: B1 = 0
Ha: B1 ≠ 0
2) één afhankelijke en méér dan één onafhankelijke variabelen
MULTIPELE LINEAIRE REGRESSIE ANALYSE SPSS pag. 88 (zelfde principe als
enkelvoudige regressie analyse)
H0: B1 = 0
H0: B2 = 0
Ha: B1 ≠ 0
Ha: B2 ≠ 0
5. Onderzoeken of de gemiddelden van méér dan twee onafhankelijke groepen van
elkaar afwijken
VARIANTIE-ANALYSE (ANalysis Of VAriance) SPSS 90
H0: B1= B2 = 0
Ha: Tenminste één B-waarde ≠ 0
De standaardfout geeft de standaardafwijking van alle mogelijke steekproefgemiddeldes
De standaardfout kan je afleiden door middel van de volgende formule: σ/√n.
De standaard fout van het gemiddelde is de standaardafwijking van een bepaalde groep
steekproefen getrokken uit de populatie. (Std. Error Mean)
Lower en upper bound berekenen:
XZ
α/2
σ
=
n
Zα/2= zie tabel, betrouwbaarheidsinterval delen door 2 en zoeken bij B naar de juiste waarde
die bij het gedeelde getal hoort. (bij kleine steekproef in t-tabel zoeken naar waarde
steekproef en bijbehorende z-waarde). LET OP DE GROOTTE VAN DE STEEKPROEF
Lower bound: Xgemiddeld verminderen met de rest van de formule
Upper bound: Xgemiddeld optellen bij de rest van de formule.
Eenzijdig toetsen: De waarden die voldoen aan de alternatieve hypothese zijn altijd groter
(of altijd kleiner) dan die van de nulhypothese.
Enkelvoudig Ho: θ = θo
H1: θ > θo
Samengesteld
Ho: θ ≤ θo
H1: θ > θo
Tweezijdig toetsen: De waarden die voldoen aan de alternatieve hypothese kunnen zowel
groter als kleiner zijn dan die van de nulhypothese.
Ho : θ = θo
H1 : θ ≠ θo
Grootte van de steekproef berekenen p. 263-264
Formule:
n
( PsQs )( Z )²
errorterm ²
N= uitkomst, grootte van de steekproef
Zα = z-score die past bij betrouwbaarheidsniveau
Ps = kans op succes
Qs= kans op mislukking
Error term = percentage waarnaar je streeft over hoeveel afwijking er mag zijn.
De grootheid Sx is in de statistiek de benaming voor de standaardafwijking van het
steekproefgemiddelde.
Formule voor de t-waarde (bij one sample t-test):
X µ0
T
n
S
Df = degrees of freedom n-1, deze moet je bij een t-test als zoekwaarde gebruiken
Kritieke waarden voor t af te lezen op p.800, niet vergeten N-1 te doen.
Wanneer een steekproef groter is dan 121 mag je ook een z-toets doen.
Kleiner dan 121 t-toets
SPSS berekent als Mean Difference altijd M1-M2, ofwel het gemiddelde van groep (a) minus
het gemiddelde van groep (b).
De regel van cochran luidt: geen van de verwachte cell count is minder dan 1 en niet meer
dan 20% is minder dan 5.
Rijtotaal*Kolomtotaal/Steekproefomvang
De R-kwadraat is de proportie(of percentage)verklaarde variantie. Dit is het percentage van
spreiding in het afhankelijk kenmerk ten aanzien van het gemiddelde van het afhankelijk
kenmerk op het onafhankelijk kenmerk. Hoe dichter bij de 1, hoe beter het deterministisch
model en hoe dichter de punten in de puntenwolk op de regressielijn liggen. .279 betekent
dat de punten in de puntenwolk relatief ver van de regressielijn afliggen. Ook wel Coefficient
of Determination.
Standard error of regression model berekenen: Je pakt uit de ANOVA bij residual de Sum of
Squares en die deel je door de df, dan kom je uit op de mean square. Als je vervolgens hier
de wortel uit trekt, komt je uit op the standard error of the estimate. (door SPSS wordt de
uitkomst de mean square genoemd)
Dit is de gemiddelde spreiding van de punten ten opzichte van de regressielijn die je
erdoorheen hebt getrokken.
Wanneer je de Sum’s of Squares in de output deelt door de bijhorende vrijheidsgraden onder
df, dan krijg je de Mean Squares die SPSS vermeldt onder ANOVA.
Uit de vrijheidsgraden kun je achterhalen wat de waarde van n is, ofwel het aantal
respondenten dat bij de regressieberekening meedoet. Anova Total (is aantal
respondenten) -1 voor elke variabele.
De intercept, oftwel Bo, is de afstand van het snijpunt met de y-as tot de oorsprong.
De B-coefficient, of de B1, is een soort richtingscoefficient; de hellingshoek van de
regressielijn.
Ŷ = b0+b1*X1
Bereken zoals uitgelegd op pagina 629 de breedte van het 95% voorspellingsinterval van
KRANTMIN wanneer we uit de populatie van alle respondenten één 30-jarige respondent
zouden nemen Hiervoor heb je de zoals je ziet de waarde van SSXX (het boek noemt dit ook
wel S2 x ) nodig.
Ŷ ± Tα/2 * S * √(1 + (1/n) + ((Xp-Xgemiddeld)^2/SSxx)
Multipele regressieanalyse
Y= B0 + B1x1 + B2x2 + B3x3 + E
Y=De afhankelijke variabele
Waarbij B1/2/3 de coefficienten van de variabelen zijn en X1/2/3 de verschillende
onafhankelijke variabelen.
En B0 het begingetal
Hoeveel procent door de kwadratensom of variantie verklaard wordt kun je aflezen aan:
model summary Rsquare
of
Regression / Total = % verklaard (ANOVA)
The model fits data very well als meer dan 20% verklaard wordt.
Variantie analyse gebruik je om te kijken of populatiegemiddelden van 3 of meer groepen
significant van elkaar verschillen, terwijl je bij multipele regressie een afhankelijke variabele zo
goed mogelijk probeert te verklaren door middel van meerdere onafhankelijke variabelen.
Formule voor F : ((SST-SSE)/k) / SSE/ ((n-(k+1))
N= grootte steekproef
SST = Totale regressie
SSE = onverklaarde regressie residual
K = het aantal onafhankelijke variabelen.
F=waarde bruikbaarheid model.( en R^2 geeft aan hoeveel % verklaard wordt)
In de tabel Coefficients staan onder B de kleinste-kwadraten-schattingen van alle
regressiecoëfficiënten. Achter (Constant) staat de waarde van het intercept.
Twaarde= B1/SB1
De standaarderror geeft weer in welke mate het coefficient van de steekproef kan afwijken
van degene van het totaal.
Cramers V wanneer deze waarde boven de 0.5 komt begint het wat voor te stellen, maar vaak is
de test ook zonder cramers V statistisch relevant vanwege de toetsingsgrootte
SIG < ALPHA: H0 verwerpen.
Bij t-toets Sig<Alpha is kijken in de rij van unequal variances en dan bij sig. Two tailed weer
vergelijken met alpha
Als Spearman’s Rho groter is dan 0.3 of kleiner is dan -0.3 dan is deze altijd relevant.
Verwachtingswaarde gemiddelde van kansverdeling gewogen gemiddelde van alle mogelijke
waarden
m = E(X) = Sx p(x)
Variantie gewogen gemiddelde gekwadrateerde afwijking van het gemiddelde
s2 = E[ (x - m)2 ] = S (x - m)2 p(x)
Beschrijvende, toetsende en verklarende statistiek, eigenlijk is het wel erg simpel?
1.
Een onderwijssocioloog heeft het vermoeden, dat des te hoger iemands opleidingsniveau is
des te geringer het aantal minuten zal zijn, dat iemand tv kijkt. Betreffende onderzoeker
heeft materiaal ter beschikking om dit vermoeden te toetsen. Welke toetsen zijn eventueel
geschikt, noem de voorwaarden waaronder deze toetsen mogen worden gebruikt, formuleer
de bijbehorende hypothesen, verwerpingsgebied (α=.01) en formuleer de conclusies van de
toetsen.
Waarden van x voorspellen aan de hand van y. toets is enkelvoudige regressie. H0: B1
=0
Ha: B1 ≠ 0. Er is een afhankelijke en een onafhankelijke variabele.
2.
Een theoloog met aanleg voor empirisch onderzoek wil weten of het al dan niet hebben van
kinderen in statistische zin een relatie heeft met het al dan niet lid zijn van een kerk of
religieuze organisatie. Hij kijkt naar het meetniveau van de kenmerken en kiest voor een
specifieke statische analysetechniek. Welke techniek is dat? Formuleer de nulhypothese en
de alternatieve hypothese, verwerpingsgebied (α=.05) en trek uw conclusie.
Kruistabel + Chi kwadraat. Relatie onderzoeken tussen kinderen en kerklid.
3.
Een communicatiewetenschapper vermoedt, dat er een verschil bestaat in het gemiddeld
aantal minuten, dat mensen zonder kinderen en mensen met kinderen, televisie kijken en
wil dat toetsen met de meest geschikte toets. De onderzoeker vermoedt, dat de verdeling
over het kenmerk Kijktijd in de twee onderzoekspopulaties als normaal mag worden
beschouwd.
Welke toets zal hij kiezen? Formuleer de nulhypothese en de alternatieve hypothese,
verwerpingsgebied (α=.05) en trek uw conclusie op basis van de toetskeuze.
Independent samples t-test. Onderzoeken of de gemiddelden van twee groepen van
elkaar afwijken. Wijkt het gemiddelde van de groep geen kinderen af van de groep
wel kinderen. Testen door, t-waarde van test te vergelijken met t-waarde uit het
boek (in dit geval voor 95%) of door sigma te vergelijken met alpha.
4.
Een sociaalpsychologe is geïnteresseerd in de samenhang tussen twee variabelen
betreffende steun uit het sociale netwerk. Welke samenhangsmaat is de meest geschikte en
waarom? Zijn de samenhangen statistisch significant en ook relevant (α=.01)? Tevens wil
betreffende onderzoekster weten of er een significant verschil bestaat voor wat betreft de
populatiegemiddelden op deze kenmerken. Welke toets kan zij gebruiken (neem aan dat
beide variabelen kwantitatief zijn) en hoe luidt haar conclusie bij een α van .01?
Spearman’s Rho. Berekenen dmv correlatie. Je wil de samenhang tussen twee
variabelen testen.
Deelvraag: paired samples t-test: Vergelijking van twee afhankelijke groepen
kijken of er een significant verschil bestaat, om verschillen op te merken moet je
vergelijken dus t-test.
5.
Een socioloog doet een poging om met behulp van secundaire analyse de kijktijd van
respondenten te voorspellen uit de leeftijd van de respondenten. Hij voert hiertoe een
statistische analyse uit, die daarvoor geknipt is. Kies de meest geschikte statistische
analysetechniek en kan de socioloog hier iets mee m.a.w. is het een statistisch significant en
vervolgens relevant voorspellingsmodel (α=.05)?
Vervolgens voert de socioloog een tweede kenmerk (hoogst voltooide opleiding) in in het
model. Hij heeft daartoe wel de aanname moeten maken, dat opleiding een kwantitatief
kenmerk is.? En levert het in statistische zin iets op?
Enkelvoudige lineaire regressieanalyse: Onderzoeken of twee kwantitatieve
variabelen verband met elkaar houden en kijken hoe sterk dit verband is. Heeft
leeftijd verband met kijktijd?
Multipele regressie analyse: één afhankelijke en méér dan één onafhankelijke
variabelen de socioloog voert een tweede kenmerk in waardoor er dus een
afhankelijke variabele is (kijktijd) en twee onafhankelijke variabelen: leeftijd en …..
6.
Een onderzoeker krijgt de beschikking over gegevens uit een onderzoek uit 2004, waarin
onder meer de variabele kijktijd voorkomt. Hij vermoedt dat de gemiddelde kijktijd
(gemiddeld aantal minuten tv kijken per dag) van de Nederlanders van 18 jaar en ouder in
vergelijking met een hem bekend gemiddelde uit 1998, namelijk 150 minuten, significant is
toegenomen. Formuleer de nulhypothese en de alternatieve hypothese,
verwerpingingsgebied (α=.10) en trek uw conclusie op basis van de toetskeuze.
One sample t-test: Onderzoeken of de waarde van een bepaald
steekproefgemiddelde afwijkt van een van tevoren verwacht theoretisch gemiddelde
(µ) onder de nulhypothese. De onderzoeker vermoedt een gemiddelde kijktijd. Nu
moet die toetsen of deze kijktijd klopt of niet. H0: μ=150 of Ha: μ≠150.
STATISTIEK B:
We laten SPSS het benodigde rekenwerk voor de t-toets doen. Klik op: Analyze Compare
Means Independent-Samples T Test v82 (schuifbalk) bovenste (Test Variable)
v133 (schuifbalk) onderste (Grouping Variable) Define Groups Klik tenslotte op
OK. Je komt nu in het output-window.
De standaardfout van het gemiddelde geeft een indicatie van de betrouwbaarheid van het
steekproefgemiddelde en wordt berekend door de standaarddeviatie te delen door de
wortel van n
Mean difference: M1-M2
Sig groter dan alpha equal variances assumed
Sig kleiner dan alpha equal variances not assumed.
Een betrouwbaarheidsinterval stelt een marge van twee uitersten waarbinnen de werkelijke
berekende waarde zal liggen. De normaalste betrouwhbaarheidsmarge is 95%, maar ook
90% en 99% worden af en toe gebruikt. Hoe hoger de betrouwbaarheid wilt stellen hoe
kleiner je marge wordt.
Paired samples t-test: er bestaat geen significant verschil tussen…… er bestaat een
significant verschil.
Mean square: Sum of squares / df
Waarde F in ANOVA: Mean square between groups/ mean square within groups.
Als de nulhypothese bij een variantie-analyse wordt verworpen, zouden we kunnen gaan
bekijken tussen welke categorieën van de onafhankelijke variabele er verschillen zijn. Dit
geschiedt met behulp van zogenaamde Post-Hoc tests. In het handboek wordt op de
pagina’s 442 t/m 444 aandacht besteed aan de Tukeytoets. Deze toets veronderstelt gelijke
steekproefomvangen per categorie van de onafhankelijke variabele. Dat is meestal niet het
geval en dan wordt er gebruik gemaakt van de toetsen van Bonferroni en Scheffé, welke
ongelijke steekproefomvangen toestaan.
Tukey: eist even grote steekproeven
Scheffé: minder significant
Bonferroni: meestal geschikt
Multipele regressievergelijking:
Regressie vraagt: in hoeverre zijn scores van het kwantitatieve variabele x te verklaren door
het kwantitatieve variabele y.
Wanneer bij een lineaire regressie 99% betrouwbaarheid wordt gevraagd moeten 99% van de scores
op 3 standaardafwijkingen van de lijn liggen.
Formule multipele regressievergelijking: Ŷi= βo+β1X1+β2X2+β3X3
Analyze Regression Linear
Via de gegeven waarde van Rsquare in de output kan je afleiden hoeveel procent woprdt
verklaard door de drie onafhankelijke variabelen tesamen.
R2= verklaarde variantie/ totale variantie
SSR
/ SST
The model fits the data very well wanneer R2 boven 0.2 als een gevonden waarde hier ver
onder ligt spreek je van een low fit.
N afleiden van df = df + 1
Ho: B1 = 0 Geen van de gegeven variabelen kan een lineair verband verklaren.
Ha: B1 ≠ 0
Bruikbaarheid model toetsen d.m.v. F-toets. Sig achter F-toets testen op alpha.
Formule F-waarde: (SSR/K)/(SSE/(n-k+1))
SSR = Sum of squares regression
K = Df bij SSR
SSE = Sum of squares residual
N= dftotal +1
Als tenminste een regressiecoefficient afwijkt van nul is het model bruikbaar. Bij regressie
analyse wil je H0 juist verwerpen want dit betekent dat er aanwijzingen zijn voor lineaire
regressie.
t-waarde: Waarde B delen door std. Error.
Lower/Upper bound berekenen: . B1±Tα * Se
Wanneer je een interactiemodel hebt en het gewone model en beide zijn significant geef je
de voorkeur aan het model met de hoogste R2
Een van de voorwaarden van een t-toets is dat de variabelen normaal verdeeld zijn. Inkomen
is (bijna) nooit normaal verdeeld en hier ook niet, dus moeten we gebruik maken van de
Wilcoxon Rang Sum Test.
Mann-Whitney test/ rank sum test
op Analyze Nonparametric Tests Legacy Dialogs 2 Independent Samples nl_inc
bovenste (Test Variable) sex onderste (Grouping Variable) Define Groups.
Continue. Ok.
SPSS geeft onder Test Statistics de z-waarde (volgens de formule op pagina 773) op basis van T1 of T2,
afhankelijk van welk van beide groepen de laagste Mean Rank heeft. Daarom is de z-waarde die SPSS
geeft altijd negatief of nul en bestaat de ‘rejection region’ bij eenzijdig toetsen uit z < -z.
We gaan de Signed Rank Test uitvoeren, in SPSS kortweg de 'Wilcoxon' genoemd. We doen daarbij
net alsof we over een steekproef van slechts 20 personen beschikken. Klik op Data Select Cases
Random sample of cases Sample Exactly. Type dan 20, klik in het lege hokje rechts en
type 5000. Klik daarna Continue OK. SPSS selecteert nu willekeurig 20 mensen uit het bestand.
Klik dan op Analyze Nonparametric Tests Legacy Dialogs 2 Related samples
wwoning wwoonomgeving (schuifbalk!) OK. Laat de resultaten in het output-window
printen.
Dummy variabelen extra variabele, hulp variabele
- Nominaal
- Ordinaal
Omzetten kenmerk in een dummy kan je opnemen in een regressie analyse.
Een interactie effect verkrijg je door te vermenigvuldigen.
Non-parametrische testen: toetsen op representativiteit, zijn minder snel met verwerpen
nulhypothese.
Chi-square nominaal
Ordinaal
H0: twee variabelen zijn statistisch onafhankelijk
Ha: twee variabelen zijn statistisch afhankelijk
Tweetal toetsen: wilcoxon / mann withney
Wilcoxon bij 2 onafhankelijke steekproefen of bij 2 afhankelijke steekrpoeven. (variabelen)
H0: P1 = P2 = P3 = …
Ha: tenminste 1 van de proporties onder H0 wijkt af. (wil je liever niet)
H0: de twee verdelingen zijn identiek/ De twee locaties zijn gelijk
Ha: de twee verdelingen zijn niet identiek / De twee locaties zijn ongelijk
Kruskall wallis/ Friedman : voor meer dan 2 variabelen
H0: μ1 = μ2 = μ3 = μ4
Ha: tenminste 1 van de gemiddelden wijkt af
Assumpties voor de uitvoering van analyse kruskall wallis/ Friedman:
σ12 = σ22= σ32 gekwadrateerde standaardafwijkingen zijn gelijk aan elkaar
Al die verdelingen zijn klokvormig in de populatie
Bij de friedman test moet je 5 variabelen vergelijken.
Cochrans regel: het aantal cellen met verwachte frequentie onder 5 ≤ 20% dan mag chi kwadraat
worden toegepast.
Nominale variabele = Uitkomst is een soort, een indeling in een bepaalde categorie.
Voorbeelden: Proefwerkcijfer, Schoenmaat . NB: soorten zijn wel numeriek te coderen!
Ordinale variabele = Uitkomst is net als bij een nominale variabele een soort, die ingedeeld
kan worden in een bepaalde categorie. Nu echter hebben deze categorieën een bepaalde
logische volgorde uitkomsten zijn rangschikbaar.
Voorbeelden: opleidingsniveau
Ratioschaal = Continue variabele met natuurlijk nulpunt
Voorbeelden: gewicht, lengte
Intervalschaal = Continue variabele zonder natuurlijk nulpunt
Voorbeelden: temperatuur in oC, tijd, bouwjaar
MEETNIVEAUS EN TOETSEN
Nominaal – Nominaal:
Chi kwadraat / Kruistabel
Cramer’s V V (0;1) V 0.5 begint wat voor de stellen. Toetsing is statistisch
onafhankelijk.
Nominaal- Ordinaal:
Chi kwadraat / Cramer’s V
Wilcoxon toets: 2 onafhankelijke steekrpoeven
Kruskall-wallis: Steekproeven ≥ 2 onafhankelijke steekproeven
Nominaal – Interval:
T-toets: twee onafhankelijke steekproeven
Variantie analyse: > 2 steekproeven. ANOVA. Zijn de scores stat. Significant.
Ordinaal – Ordinaal:
Spearman Rs (-1; +1) als < -.3 ; > .3 begint het wat voor te stellen
Wilcoxon 2 related samples (chi-kwadraat/ cramer’s V)
Ordinaal – Interval/Ratio:
Variantie analyse
Paired samples t-test
>3 ordinale variabele in verband friedmantest
Mogelijk ook Kruskall-wallis.
Interval/Ratio – Interval/Ratio:
R Pearson R(-1 ; +1)
Regressie-analyse
Samenhang: Correlate of kruistabel
Score voorspellen heeft met een andere te maken regressie analyse
Variantie-analyse: ANOVA: F-toets
2 related samples bij verschil verdelingen van kenmerken: Wilcoxon.
SPEARMAN: ORDINAAL
PEARSON: INTERVAL
Toetsende en verklarende statistiek, een vijftal vragen.
1.
Een onderwijssocioloog heeft het vermoeden, dat er een verschil bestaat tussen het gemiddeld
aantal minuten, dat mensen tv kijken, indien een opsplitsing plaatsvindt naar opleidingsniveau.
Betreffende onderzoeker heeft materiaal ter beschikking om dit vermoeden te toetsen. Welke
toetsen zijn eventueel geschikt, noem de voorwaarden waaronder deze toetsen mogen worden
gebruikt en formuleer de bijbehorende hypothesen.
Gemiddeld minuten interval
Opleidingsniveau ordinaal
Toets: variantie analyse: compare means, anova.
Wanneer geen symmetrisch klokvormige verdeling kruskall wallis.
2.
Een theoloog met aanleg voor empirisch onderzoek wil weten of het al dan niet hebben van kinderen
in statistische zin een relatie heeft met het al dan niet lid zijn van een kerk of religieuze organisatie.
Hij kijkt naar het meetniveau van de kenmerken en kiest voor een specifieke statische
analysetechniek. Welke techniek is dat? Formuleer de nulhypothese en de alternatieve hypothese.
2 kenmerken statistisch afhankelijk
Nominaal – Nominaal
Correlate, bivariate.
Pearson.
3.
Een communicatiewetenschapper vermoedt, dat er een verschil bestaat in het gemiddeld aantal
minuten, dat mensen zonder kinderen en mensen met kinderen, televisie kijken en wil dat toetsen
met de meest geschikte toets. De onderzoeker vermoedt, dat de verdeling over het kenmerk Kijktijd
in de twee onderzoekspopulaties als normaal mag worden beschouwd.
Welke toets zal hij kiezen? Formuleer de nulhypothese en de alternatieve hypothese.
Interval – Nominaal
Parametrische toets hier t-toets
4.
Een sociaalpsychologe is geïnteresseerd in de samenhang tussen twee variabelen betreffende steun
uit het sociale netwerk. Betreffende variabelen luiden in vraagvorm als volgt:
1. ‘Ik kan altijd met mijn problemen bij iemand terecht’
2. ‘Ik heb genoeg mensen om me heen, die me kunnen helpen
De antwoordmogelijkheden op deze variabelen zijn; 1. altijd, 2. vaak, 3 soms, 4 bijna nooit, 5 nooit.
Welke samenhangsmaat is de meest geschikte en waarom? Tevens wil betreffende onderzoekster
weten of er een significant verschil bestaat voor wat betreft de verdelingen op deze kenmerken.
Welke toets kan zij gebruiken?
Gradatie, rangorde.
2 ordinale kenmerken samenhang correlate
Spearman.
5.
Een socioloog doet een poging om met behulp van secundaire analyse de kijktijd van respondenten
te voorspellen uit de leeftijd van de respondenten. Hij voert hiertoe een statistische analyse uit, die
daarvoor geknipt is.
Vervolgens voert de socioloog een tweede kenmerk (geslacht) in in het model. Dit mag niet zo maar.
Hij heeft daartoe wel dit kenmerk geslacht moeten transformeren van een kwalitatief kenmerk naar
een kwantitatief kenmerk.
Voorspelling: Regressie-analyse.
Deel 2:
Recode, compute, dummy
Kenmerk geslacht meevoeren.
Verklaringskracht hetzelfde.
Compute variabele: compute, function Group, All, Mean
Mean( v… , v… , v… )












