Wiskunde – krachten als vectoren – oefeningensessie 1

Wiskunde – krachten als vectoren – oefeningensessie 1
Bron: Wiskunde in de bouw – Jos Ariëns, Daniël Baldé
Oefening 1
Een groot nieuw brugdek van 40m lang moet over een rivier geplaatst worden. Eén kraan alleen kan
dit onmogelijk doen en daarom moet er aan beide kanten van de rivier een kraan komen te staan.
Het contragewicht van de kraan is al berekend en dit gewicht is groot genoeg om de kraan stabiel te
laten staan. Het is echter nog maar de vraag of de kabels het gewicht onder die omstandigheden
kunnen dragen.
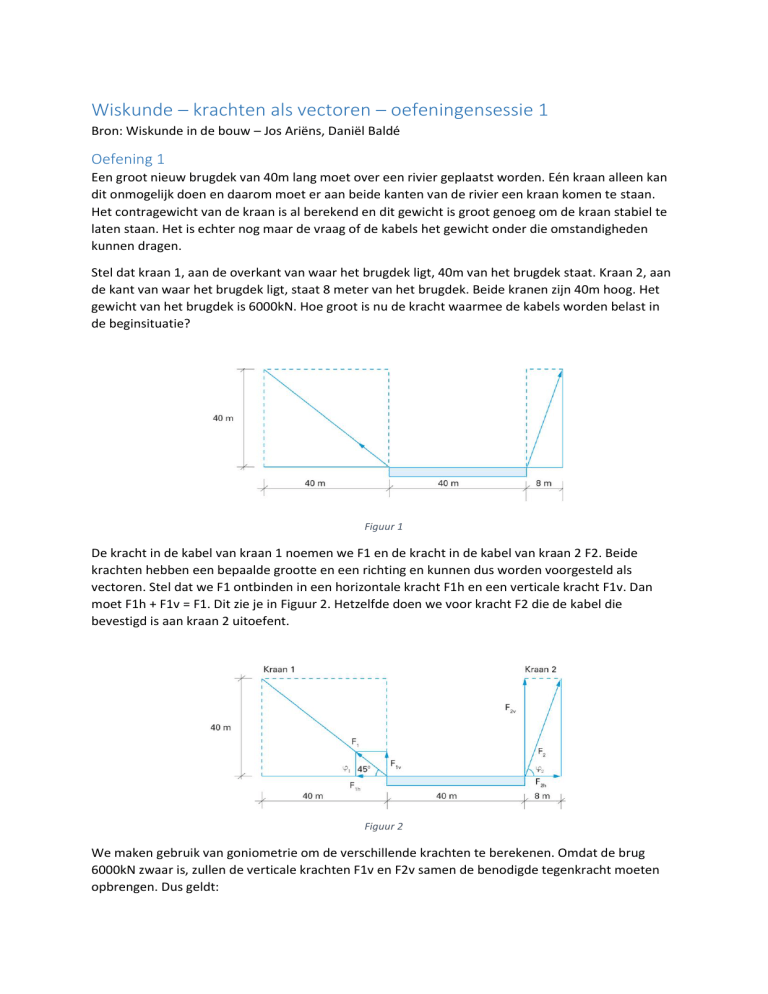
Stel dat kraan 1, aan de overkant van waar het brugdek ligt, 40m van het brugdek staat. Kraan 2, aan
de kant van waar het brugdek ligt, staat 8 meter van het brugdek. Beide kranen zijn 40m hoog. Het
gewicht van het brugdek is 6000kN. Hoe groot is nu de kracht waarmee de kabels worden belast in
de beginsituatie?
Figuur 1
De kracht in de kabel van kraan 1 noemen we F1 en de kracht in de kabel van kraan 2 F2. Beide
krachten hebben een bepaalde grootte en een richting en kunnen dus worden voorgesteld als
vectoren. Stel dat we F1 ontbinden in een horizontale kracht F1h en een verticale kracht F1v. Dan
moet F1h + F1v = F1. Dit zie je in Figuur 2. Hetzelfde doen we voor kracht F2 die de kabel die
bevestigd is aan kraan 2 uitoefent.
Figuur 2
We maken gebruik van goniometrie om de verschillende krachten te berekenen. Omdat de brug
6000kN zwaar is, zullen de verticale krachten F1v en F2v samen de benodigde tegenkracht moeten
opbrengen. Dus geldt:
F1v + F2v = 6000kN
Om ervoor te zorgen dat de brug stil hangt en niet naar links of rechts beweegt, moeten de
horizontale krachten F1h en F2h elkaar in evenwicht houden. Dit wil zeggen:
F1h + F2h = 0kN
Kijken we naar de kabel van kraan 1 dan zien we dat deze onder een hoek van 45° gespannen is. De
richting van de kabels bepaalt dus de richting van de vectoren waar we mee rekenen.
Figuur 3
De hoek van de kabel van kraan 2 bepalen we door te stellen dat tanϕ2 = 40/8 = 5. Met behulp van
arctan 5 =79°, hebben we ook ϕ2 gevonden.
Met goniometrie kunnen we zien dat de voorwaarde F1h + F2h = 0 ook geschreven kan worden als:
F1 . cos45° + F2 . cos 79° = 0
Figuur 4
Vervolgens kunnen we F1v + F2v = 6000kN ook schrijven als:
F1 . sin45° + F2 . sin79° = 6000kN
De volgende stap is voor cos45°, cos79°, sin45° en sin79° de juiste waarden invullen in de
bovenstaande formules. Dit wordt dan:
1. -0,71F1 + 0,19F2 = 0
2. 0,71F1 + 0,98F2 = 6000kN
Wanneer we vergelijking 1 optellen bij vergelijking 2 krijgen we:
(0,98 + 0,19)F2 = 6000kN
Dus betekent F2 = 5128kN en F1 = 1372kN
De kabel van kraan 1 moet dus minimaal een trekkracht van 1372kN hebben plus een
veiligheidsmarge kunnen opnemen en de kabel van kraan 2 een trekkracht van 5128kN plus een
veiligheidsmarge.
Oefening 2
Een voorwerp met een gewicht van 50kN hangt in rust aan twee kabels. We kunnen de spankrachten
F1 en F2 in de kabel berekenen via de horizontale en verticale krachtsevenwichten. Eerst
schematiseren we het probleem (zie Figuur 5): we stellen de kracht voor als een gericht lijnstuk en
we plaatsen een x-as en een y-as.
Figuur 5
Omdat het voorwerp in rust aan de kabel hangt, geldt de som van alle horizontale
krachtscomponenten nul moet zijn, evenals de som van alle verticale krachtscomponenten. Hieruit
volgen de twee evenwichtsvergelijkingen. Ga na dat deze evenwichtsvergelijkingen als volgt luiden:
1
1. − 2 √2𝐹1 +
2.
1
√3𝐹2
2
1
1
√2𝐹1 − 2 √3𝐹2
2
= 0𝑘𝑁
= 50𝑘𝑁
Dit stelsel van twee vergelijkingen met twee onbekenden is op te lossen via eliminatie van één van
de twee onbekenden. We kunnen bevoorbeeld de twee vergelijkingen bij elkaar optellen. Bereken nu
zelf de krachten F1 en F2.
(antwoord: F2= 136,6kN en F1=167,3kN)
Oefening 3
Voor het maken van een kelder onder een gebouw wordt een 5 meter diepe bouwput gegraven.
Door middel van damwanden wordt voorkomen dat er grond in de bouwput valt. De damwanden
ondervinden een kracht door de gronddruk, die toeneemt met de diepte, zie Figuur 6. Op een diepte
van 5meter is de gronddruk 5kN.
Figuur 6
1. Bepaal de totale gronddruk op 1 strekkende meter damwand in kN per strekkende meter.
(antwoord: 12,5kN/m)
2. Je kunt de gronddruk, die met een diepte varieert, vervangen door één kracht F. Hoe groot is
die kracht en waar grijpt ze aan? (antwoord: 12,5kN/m op een diepte van 3,3m diepte)
3. Kracht F veroorzaakt een moment (kracht x arm) ten opzichte van punt A. Hoe groot is dit
moment? (antwoord: 20,8kNm)
Oefening 4
Aan de gevel van een oude woning is een balk bevestigd die gebruikt wordt om meubels en dozen
naar boven te hijsen. De balk heeft een lengte van 1,5 meter en wordt ondersteund door een schoor
onder een hoek van 35°, zie Figuur 7 . Een meubelstuk oefent een kracht uit van 500N naar beneden.
Figuur 7
We gaan ervan uit dat de balk AC alleen horizontale krachten opneemt en geen verticale kracht in A
oplevert. Technisch is dat niet geheel correct, maar op deze manier kunnen we wel de maximale
kracht in BC berekenen. Hoe groot is de kracht in schoor BC wanneer de last van 500N stil hangt?
Hoe groot is de kracht in balk AC? (antwoord: kracht in schoor BC is 610N, kracht in balk AC is 350N)
Oefening 5
In een kraan van 10m hoog hangt een heipaal van beton met een gewicht van 2kN. Door de opstekende
wind wordt er een horizontale kracht van 0,4kN op de paal uitgeoefent. Welke hoek maakt de kabel
ten opzichte van de loodlijn (de lijn die loodrecht staat op het horizontale vlak)? (antwoord: 11,3°)
Figuur 8
Oefening 6
Een televisiemast met een hoogte van 25m wordt belast door een windbelasting die eruitziet als
Figuur 9 . Boven in de mast is de windkracht het grootst, namelijk 500N per strekkende meter mast
en bij het maaiveld is de wind vrijwel 0N/m.
Figuur 9
1. Hoe groot is de totale windkracht op de mast? Als je de verdeelde windkracht vervangt door
een puntkracht die net zo groot is, wat is het aangrijpingspunt? (antwoord: 6250N/m op
16,67m)
2. Op een hoogte van 20m worden drie kabels bevestigd onder een hoek van 45°. De kabels
kunnen alleen trekkracht opnemen. Hoe groot is de maximale kracht in een kabel ten
gevolge van de wind? (antwoord: 8839N)
Oefening 7
Een man van 80kg die op een schuin dak staat, oefent een kracht van ~800N uit op dit dak. De
dakhelling bedraagt 30°. Bereken de kracht die de man uitoefent loodrecht op het dakvlak door het
gewicht te ontbinden in een kracht parallel aan het dakvlak en een kracht loodrecht op het dakvlak.
(antwoord: 693N)
Oefening 8
Op een dak met een helling van 45° ligt een laag sneeuw van 15cm dik. De sneeuw oefent een kracht
uit van 0,15kN/m² op het dakvlak. Daarnaast waait er een wind die een horizontale kracht op het dak
uitoefent van 0,1kN/m².
Sneeuw en wind oefenen beide een kracht uit op de dakbalken. Hoe groot zijn de krachten F1 en F2,
ten gevolge van de combinatie van wind en sneeuw op 1 strekkende meter balk? (antwoord:
F1=0,177kN; F2=0,035kN)
Figuur 10