Hoofdstuk 7 Goniometrie

er
sb
v
Hoofdstuk 7 Goniometrie
Hoofdstuk 7 Goniometrie
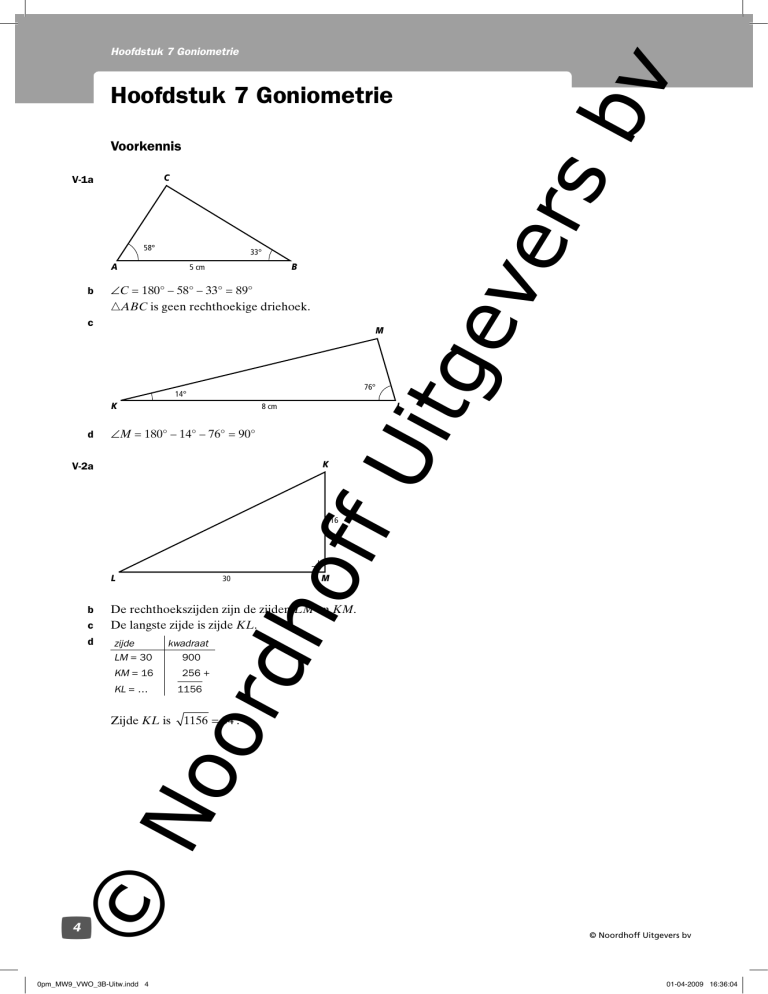
Voorkennis
V-1a
C
58°
33°
∠C = 180° – 58° – 33° = 89°
ABC is geen rechthoekige driehoek.
M
76°
14°
K
d
Ui
tg
b
c
B
5 cm
ev
A
8 cm
∠M = 180° – 14° – 76° = 90°
L
K
V-2a
L
b
c
d
De rechthoekszijden zijn de zijden LM en KM.
De langste zijde is zijde KL.
zijde
LM = 30
kwadraat
900
KM = 16
256 +
1156
or
KL = …
Zijde KL is
1156 = 34 .
©
No
M
dh
30
off
16
⁄
4
0pm_MW9_VWO_3B-Uitw.indd 4
© Noordhoff Uitgevers bv
01-04-2009 16:36:04
zijde
AB = 7
kwadraat
49
BC = 9
81 +
H
zijde
GH = 4
kwadraat
16
HI =
c
90
90
I
GI = 74
zijde
KM = 20
kwadraat
400
KL = 15
225 +
LM = …
625
LM = 625 = 25
V-4a
In ADC:
zijde
AD = 5
75 +
100
AC = 10
L
M
20
15
K
kwadraat
144
dh
zijde
BD = 12
75 +
75
219
BC = …
BD = 219 ≈ 14, 8
V-5a
zijden van ABC
zijden van DEF
Je moet met 0,5 vermenigvuldigen.
De overeenkomstige hoeken zijn gelijk.
or
AB = 12
DE = 6
BC = 10
DF = 5
AC = 11
EF = 5,5
No
©
c
G
?
CD = 75
Ze gebruikt CD = 8,7, maar dat is een afgerond getal, want 75 ≈ 8,660254…
Als ze CD = 75 gebruikt, krijgt ze wel een nauwkeurig antwoord.
CD =
b
4
?
kwadraat
25
CD = …
b
c
d
90
74 +
GI = …
B
7
ev
b
A
AC = 130
9
Ui
tg
?
130
AC = …
C
off
V-3a
er
sb
v
Hoofdstuk 7 Goniometrie
© Noordhoff Uitgevers bv
0pm_MW9_VWO_3B-Uitw.indd 5
⁄
5
01-04-2009 16:36:06
b
c
zijden van ABC
zijden van HIG
AB = …
HI = 3,1
BC = 4
GI = …
AC = 6
GH = 4
De zijden van ABC zijn met factor 4 : 6 = 23 vermenigvuldigd.
AB = 3,1 : 23 = 4,65
GI = 4 × 23 = 2 23
∠B = 88° (zie opdracht a)
∠K = ∠D (overeenkomstige hoeken) dus ∠K = 55°
∠M = 180° – 101° – 55° = 24°, ∠F = ∠M (overeenkomstige hoeken), dus ∠F = 24°
ev
ABC is gelijkvormig met HIG, want ∠B = 180° – 42° – 50° = 88° en

∠G = 180° – 88° – 42° = 50°, dus de overeenkomstige hoeken zijn gelijk.
DEF is gelijkvormig met KLM, want de overeenkomstige zijden zijn met
dezelfde factor vermenigvuldigd, namelijk 1,5.
Ui
tg
V-6a
er
sb
v
Hoofdstuk 7 Goniometrie
7-1 Tangens
f
2a
De hoek is 21°.
dh
1a
off
ij drie treden hoort een afstand van 3 × 40 = 120 cm en
B
een hoogte van 3 × 15 = 45 cm.
b Nee, de helling blijft gelijk.
cBij 13 treden hoort een afstand van 13 × 40 = 520 cm en
een hoogte van 13 × 15 = 195 cm.
d Bij één trede hoort een afstand van 40 cm en een hoogte van 15 cm.
hoogte
hoogte 195
eBij opdracht a is
= 45 = 0, 375 , bij opdracht c is
=
= 0, 375 en
afstand 120
afstand 520
hoogte 15
bij opdracht d is
=
= 0, 375 .
afstand 40
De deling levert telkens dezelfde uitkomst op.
20 = 0, 4 geeft afstand = 20 = 50 .
afstand
0, 4
20 cm
De treden zijn 50 cm diep.
b De hellingshoek is 22°.
c Nee, dat is niet van belang.
d Hoe groter het hellingsgetal, hoe groter de hellingshoek.
or
I n de tekening hiernaast is de schaal 5 cm : 2500 m,
dus 1 cm : 500 m.
De hoogte is gemeten 2,9 cm, dus de hoogte is
2,9 × 500 = 1450 m.
b tan 30° = 1450
≈ 0, 6
2500
cBij deze kabelbaan is de hoogte 2900 m.
De tangens van deze hellingshoek is 2900
= 1, 16 .
2500
3a
©
No
50 cm
⁄
6
0pm_MW9_VWO_3B-Uitw.indd 6
30°
2500 m
© Noordhoff Uitgevers bv
01-04-2009 16:36:08
d
er
sb
v
Hoofdstuk 7 Goniometrie
ee, de hoek is niet twee keer zo groot, zoals na te meten is
N
in de tekening hieronder is de hoek ongeveer 50°.
ev
1450 m
30°
2500 m
4a
b
Met de rekenmachine is tan 30° ≈ 0,577, dus dat klopt
met het antwoord van opdracht 3b.
Met de rekenmachine is tan–1(1,2) ≈ 50°. Dat klopt met
het antwoord van opdracht 3c.
Zie de schets hiernaast.
b tan ∠H = 117
cRanita vindt 7,44°.
Divya vindt 32°.
Jonny vindt 33°.
d Divya vindt de juiste hellingshoek.
off
5a
6Schets:
dh
50
tan ∠H = 650
−1 50
tan ( 650 ) ≈ 4, 4
De hellingshoek is 4°.
chets:
S
15
tan ∠H = 120
15
tan −1 ( 120
) ≈ 7, 1
De hellingshoek is 7°.
chets:
S
tan ∠H = 15
80
tan −1 ( 15
)
≈
10, 6
80
De hellingshoek is 11°.
©
b
No
7a
© Noordhoff Uitgevers bv
0pm_MW9_VWO_3B-Uitw.indd 7
7m
H
11 m
50 m
H
650 m
or
Ui
tg
1450 m
15 m
H
120 m
15 m
H
80 m
⁄
7
01-04-2009 16:36:10
7-2 De tangens gebruiken
8a
Q
26
10
?
P
R
24
btan ∠P =
∠P ≈ 23°
10
24
9a
10tan ∠A =
∠A ≈ 23°
zijde
15
kwadraat
225
64 +
…
289
17
off
tan∠B = 115
∠B ≈ 24°
3
7
Ui
tg
tan–1( 68 ) ≈ 36,9 dus ∠A = 37°.
b Zijde AC is de overstaande rechthoekszijde van hoek B.
c Zijde BC is de aanliggende rechthoekszijde van hoek B.
dtan∠B = 86
∠B ≈ 53°
e ∠B = 180° – 90° – 37° = 53°
ev
er
sb
v
Hoofdstuk 7 Goniometrie
zijde
7
kwadraat
49
16 +
…
dh
De aanliggende rechthoekszijde van hoek C is 8.
tan ∠C = 158
∠C ≈ 62°
11a
b
12a
tan ∠A = 53
tan ∠B = 45
∠A ≈ 59°
∠B ≈ 51°
In driehoek ABC zijn de hoeken samen 180°, dus ∠C = 180° – 59° – 51° = 70°.
No
or
65
65
De overstaande rechthoekszijde van hoek D is 4.
tan ∠D = 47
∠D ≈ 30°
tan 13° = 110
a
a=
110
tan 13°
©
a ≈ 476 m
bOp een afstand van 476 meter spelen enkele centimeters geen rol van betekenis. Ook
is het waarschijnlijk dat de hoogte van 110 meter en de hoek van 13° al zijn afgerond.
⁄
8
0pm_MW9_VWO_3B-Uitw.indd 8
© Noordhoff Uitgevers bv
01-04-2009 16:36:12
er
sb
v
Hoofdstuk 7 Goniometrie
13
40 m
7°
a
tan 7° = 40
a
40
tan 7°
a=
a ≈ 326 m
De afstand van het schip tot de vuurtoren is ongeveer 326 meter.
ev
e kabelbaan van Coq naar Ballon gaat omhoog want Coq ligt op 1830 meter
D
hoogte en Ballon ligt op 2520 meter hoogte.
bDe horizontale afstand is 3,6 cm. Dat is in werkelijkheid 3,6 × 50 000 = 180 000 cm en
dat is 1800 meter.
cVoor de kabelbaan van Coq naar Ballon is het hoogteverschil 2520 – 1830 = 690 m.
690
tan ∠C = 1800
∠C ≈ 21°
dVoor de kabelbaan van Douce naar Azur is het hoogteverschil 2640 – 2120 = 520 m.
De horizontale afstand is 1,6 cm, dat is in werkelijkheid 800 m.
tan ∠A = 520
800
∠A ≈ 33°
Voor de kabelbaan van Douce naar Ballon is het hoogteverschil 2520 – 2120 = 400 m.
De horizontale afstand is 3,1 cm, dat is in werkelijkheid 1550 m.
400
tan ∠B = 1550
∠B ≈ 14°
De kabelbaan van Douce naar Azur heeft de grootste hellingshoek.
14a
dh
off
Ui
tg
7-3 Sinus en cosinus
De zijden van ABC zijn allemaal met dezelfde factor vermenigvuldigd, namelijk 2.
∠A = ∠D, ∠B = ∠E en ∠C = ∠F
15a
b
c
d
e
f
g
LM = 27 = 0, 75 KL 36
DE = 48 = 0, 8
DF 60
LM = 27 = 0, 6 KM 45
M
KL = 36 = 0, 8
KM 45
45 mm
27 mm
Iets nauwkeuriger: de delingen van de overeenkomstige zijden
geven dezelfde uitkomst.
Bij de delingen EF , BC en LM krijg je de tangens.
DE AB
KL
©
EF = 36 = 0, 6 DF 60
BC = 18 = 0, 75 BC = 18 = 0, 6 AB = 24 = 0, 8
AB 24
AC 30
AC 30
Bijvoorbeeld met factor 1,5, zie de tekening hiernaast.
No
EF = 36 = 0, 75 DE 48
or
© Noordhoff Uitgevers bv
0pm_MW9_VWO_3B-Uitw.indd 9
K
36 mm
L
⁄
9
01-04-2009 16:36:14
5
12
sin ∠P =
bsin–1( 135 ) = 23°
c
d
tan ∠P =
cos–1( 12
) = 23°
13
tan ∠Q =
10
12
cos ∠R =
5
7
dus ∠R ≈ 44°
cos ∠S =
9
11
dus ∠S ≈ 35°
18a
b
tan ∠C1 = 68 dus ∠C1 ≈ 37°
cos ∠C2 = 158 dus ∠C2 ≈ 58°
Nee, want ∠C = 37° +58° = 95°
19a
dus ∠Q ≈ 40°
AE = 15
225 +
BE = …
369
dh
BE = 369 ≈ 19, 2
9
tan ∠BEC = 369
dus ∠BEC ≈ 25°
BE =
kwadraat
369
369
81 +
BC = 9
450
or
CE = …
CE = 450 ≈ 21, 2
sin ∠ECD =
20a
b
19
450
dus ∠ECD ≈ 64°
Zie de tekening hiernaast.
PQ
tan ∠PRQ =
QR
No
g
off
kwadraat
144
zijde
tan–1( 125 ) = 23°
∠E1 = ∠AEB, ∠E2 = ∠BEC, ∠E3 = ∠CED
∠C1 = ∠BCE, ∠C2 = ∠DCE
15
tan ∠ABE = 12
dus ∠ABE ≈ 51°
∠BEA = 180° – 90° – 51° = 39°
zijde
AB = 12
e
f
12
13
dus ∠P ≈ 35°
4
7
b
c
d
cos ∠P =
∠P ≈ 23°
In STU zijn slechts de overstaande zijde en de langste zijde gegeven.
sin ∠S = 178 dus is ∠S ≈ 28°
17sin ∠P =
c
5
13
ev
16a
Ui
tg
er
sb
v
Hoofdstuk 7 Goniometrie
tan ∠PRQ =
4
3
dus ∠PRQ ≈ 53°
©
cOmdat de driehoeken PQR en RST
gelijkvormig zijn geldt ∠RTS = ∠PRQ
dus ∠RTS ≈ 53°
⁄
10
0pm_MW9_VWO_3B-Uitw.indd 10
T
8
7
6
5
S
R
P
Q
4
3
2
1
O
1
2
3
4
5
© Noordhoff Uitgevers bv
01-04-2009 16:36:17
7-4 Rekenen in rechthoekige driehoeken
er
sb
v
Hoofdstuk 7 Goniometrie
d
e
21a
cos 27° = 8
AC
8
Uit cos 27° = 8 volgt AC =
dus AC ≈ 9,0.
AC
cos 27°
22Uit cos 59° =
3 volgt BC =
3
dus BC ≈ 5,8
BC
cos 59°
Uit tan 27° = EF
5
Uit sin 31° = LM volgt LM = 10 × sin 31° dus LM ≈ 5,2
10
dus YZ ≈ 9,3
Uit sin 40° = 6 volgt YZ = 6
YZ
sin 40°
Uit tan 88° = 30 volgt IG = 30
dus IG ≈ 1,0
IG
tan 88°
QR
Uit cos 63° =
volgt QR = 10 × cos 63° dus QR ≈ 4,5
10
Ui
tg
volgt EF = 5 × tan 27° dus EF ≈ 2,5
23a
b
Uit tan 35° = CD volgt CD = 6 × tan 35° dus CD ≈ 4,2.
6
sin ∠B = 45,,25 dus ∠B ≈ 50°
c
AB = AD + DB
dh
CD = 4,2
17,64 +
BC = 5,5
30,25
DB = 12, 61 ≈ 3, 6
AB = 6 + 3,6 = 9,6
oppervlakte ABC = 9,6 × 4,2 : 2 = 20,16
24a
F
No
kwadraat
12,61
or
d
zijde
DB = …
off
ev
AC is de langste zijde.
b De lengte is gegeven van de aanliggende rechthoekszijde van ∠A.
cVoor sin 27° en cos 27° heb je de lengte van de overstaande rechthoekszijde
nodig en die is niet gegeven.
8
c
55°
D
b
c
E
De driehoek heeft geen rechte hoek.
Zie de tekening bij opdracht a.
©
G
55°
© Noordhoff Uitgevers bv
0pm_MW9_VWO_3B-Uitw.indd 11
⁄
11
01-04-2009 16:36:20
er
sb
v
Hoofdstuk 7 Goniometrie
dDGF heeft een rechte hoek. Verder is in deze driehoek een zijde en een hoek
gegeven.
DG volgt DG = 8 × cos 55° dus DG ≈ 4,59
8
DE = 2 × 4,59 ≈ 9,2
eUit cos 55° =
e kan verder rekenen met de hoogtelijnen uit Q en R (dus in plaatje 1 en 3).
Z
In beide gevallen kun je gebruik maken van de zijde OR = 13.
De hoogtelijn uit P kun je niet gebruiken, want dan kun je zijde OR niet meer
gebruiken.
bMet de hoogtelijn uit Q:
Noem de hoogtelijn QS.
Uit cos 59° = RS volgt RS = 13 × cos 59° dus RS ≈ 6,7
13
QS
Uit sin 59° =
volgt QS = 13 × sin 59° dus QS ≈ 11,1
13
11, 1
11, 1
volgt PS =
dus PS ≈ 10,0
PS
tan 48°
Uit tan 48° =
PR = 10,0 + 6,7 = 16,7
26a
Zie de schets hiernaast.
b
P
∠P = 180° – 78° – 84° = 18°
Uit sin 18° =
off
Uit sin 84° = AW volgt AW = 120 × sin 84°
120
dus AW ≈ 119,3 m
119, 3
119, 3
volgt WP =
WP
sin 18°
dus WP ≈ 386 m
dh
ev
25a
Ui
tg
A
78°
84°
W
120 m
M
7-5 Gemengde opdrachten
14
100
, dus
14
een hellingshoek van tan–1( 100
) ≈ 8°.
bBij een helling van 100% stijg je 100 m over een horizontale afstand van 100 m.
Bij een helling van 14% hoort een tangens van
or
27a
28a
De tangens is dan
100
100
, en de hellingshoek is tan–1(1) = 45°.
No
10
X
80°
P
V
©
11
⁄
12
0pm_MW9_VWO_3B-Uitw.indd 12
W
© Noordhoff Uitgevers bv
01-04-2009 16:36:22
bUit cos 80° =
XP volgt XP = 10 × cos 80° dus XP ≈ 1,7.
10
Uit sin 80° = VP volgt VP = 10 × sin 80° dus VP ≈ 9,8.
10
zijde
PW = …
kwadraat
24,0
97,0 +
VP = 9,85
121
VW = 11
ev
Ui
tg
PW = 24, 0 ≈ 4,9
WX = 1,7 + 4,9 = 6,6
er
sb
v
Hoofdstuk 7 Goniometrie
29Kies de loodlijn door de top van de berg naar punt D op zijde AB.
Uit tan 40° = 1350 volgt AD = 1350 dus AD ≈ 1609 m.
AD
tan 40°
Uit tan 22° = 1350 volgt BD = 1350 dus BD ≈ 3341 m.
BD
tan 22°
De tunnel zal ongeveer 1609 + 3341 = 4950 meter lang worden.
30Kies de loodlijn uit punt L naar punt N op KM.
Uit sin 49° = LN volgt LN = 570 × sin 49° dus LN ≈ 430 m.
570
Uit cos 49° = MN volgt MN = 570 × cos 49° dus MN ≈ 374 m.
570
KN = KM – NM = 630 – 374 = 256 m
31a
LN = 430
184 900 +
KL = …
250 436
De afstand punt K naar punt L is ongeveer
250 436 ≈ 500 meter.
Uit tan 45° = b volgt b = 14 × tan 45° dus b = 14 m.
14
De lengte van het brugdek is 2 × 14 = 28 meter.
14 volgt k = 14
dus k ≈ 19,8 m
k
cos 45°
De buitenste kabels zijn ongeveer 19,8 meter lang.
bUit cos 45° =
Uit cos 30° = 14 volgt k = 14
dus k ≈ 16,2 m.
k
cos 30°
De middelste kabels zijn ongeveer 16,2 meter lang.
Uit cos 15° = 14 volgt k = 14
dus k ≈ 14,5 m.
k
cos 15°
De binnenste kabels zijn ongeveer 14,5 meter lang.
©
No
kwadraat
65 536
dh
zijde
KN = 256
or
off
© Noordhoff Uitgevers bv
0pm_MW9_VWO_3B-Uitw.indd 13
⁄
13
01-04-2009 16:36:25
tan 89° ≈ 57, 3 tan 89, 9° ≈ 573, 0 b Zie de schets hiernaast.
Met ∠P = 90° is er geen rechthoekige driehoek
meer te maken. Als ∠P bijna 90° is, is de
overstaande rechthoekszijde heel groot.
ctan 80° ≈ 5,7
tan 40° ≈ 0,8
Onno heeft geen gelijk.
33a
zijde
AB = 4
144 +
AC = 160
160
BC =
P
kwadraat
16
BC = …
tan 89, 99° ≈ 5729, 6
ev
32a
144 = 12
Dus BM = 12 : 2 = 6.
Ui
tg
er
sb
v
Hoofdstuk 7 Goniometrie
Uit tan ∠MAB = 64 volgt ∠MAB ≈ 56°.
bUit tan ∠BAC = 124 volgt ∠BAC ≈ 72°.
∠MAC = ∠BAC – ∠MAB ≈ 72° – 56° ≈ 16°
csin ∠BAC =
12
160
en sin ∠C =
4
160
dus de bewering sin ∠BAC = 3 × sin ∠C is waar.
∠C = 90° – 72° = 18° en 3 × ∠C = 3 × 18° = 54° en omdat ∠BAC = 72° is bewering B
niet waar.
34a
b
Bij ‘langsparkeren’ hoort een hoek van 0° en bij ‘haaksparkeren’ een hoek van 90°.
Q
off
dh
2,25 m
32°
P
c
or
2, 25
2, 25
volgt PR =
dus PR ≈ 4,25 m.
PR
sin 32°
ie de schets van ABC hiernaast.
Z
Uit sin 32° =
A
B
Uit sin 32° = AB volgt AB = 2, 25 × sin 32°
2, 25
dus AB ≈ 1,19 m.
No
R
N
M
2,25 m
32°
32°
4,60 m
C
©
L
⁄
14
Uit cos 32° = NM volgt NM = 4, 60 × cos 32° dus NM ≈ 3,90 m.
4, 60
0pm_MW9_VWO_3B-Uitw.indd 14
© Noordhoff Uitgevers bv
01-04-2009 16:36:28
er
sb
v
Hoofdstuk 7 Goniometrie
dAls je de lengte van BN deelt door de lengte van PR, dan krijg je het aantal
parkeerplaatsen op 1 na, oftewel aantal = 1 + BN .
PR
Verder is BN = 100 – AB – NM. Dit invullen geeft aantal = 1 + 100 − AB − NM .
PR
eaantal = 1 +
100 − 1, 19 − 3, 90
≈ 23, 33
4, 25
Je kunt maximaal 23 parkeerhavens maken.
ev
Test jezelf
Ui
tg
315
T-1atan ∠A = 1000
∠A ≈ 17°
Dit sportvliegtuig vertrekt onder een hoek van ongeveer 17°.
btan 18° ≈ 0,325, dus dit sportvliegtuig is na 1 km op een hoogte van 325 meter.
Dat is ongeveer 10 meter hoger dan het eerste sportvliegtuig.
3500
ctan ∠B = 17000
∠B ≈ 12°
De piloot moet onder een dalingshoek van ongeveer 12° op Terlet aanvliegen.
T-2aUit tan 74° = a volgt a = 40 × tan 74° dus a ≈ 139 m.
40
43 volgt a = 43
dus a ≈ 221,2 m.
a
tan 11°
De schipper is ongeveer 221 meter van die vuurtoren af.
bUit tan 11° =
T-3sin ∠A = 73 ∠A ≈ 25°
T-4Uit sin 35° =
sin ∠B = 105 cos ∠C = 246 ∠B = 30°
∠C ≈ 76°
sin ∠D = 53 ∠D ≈ 37°
sin ∠E = 63 sin ∠F =
∠E = 30°
∠F ≈ 59°
3
3, 5
AC volgt AC = 9 × sin 35° dus AC ≈ 5,2.
9
or
dh
Uit tan 68° = b volgt b = 40 × tan 68° dus b ≈ 99 m.
40
De afstand tussen de bootjes is ongeveer 139 – 99 = 40 meter.
off
7
Uit tan 50° = 7 volgt FE =
dus FE ≈ 5,9.
FE
tan 50°
No
Uit sin 20° = 3 volgt KL = 3
dus KL ≈ 8,8.
KL
sin 20°
Uit cos 70° = PR volgt PR = 12 × cos 70° dus PR ≈ 4,1.
12
Trek in VWX een hoogtelijn WP op zijde VX.
Uit sin 50° = WP volgt WP = 16 × sin 50° dus WP ≈ 12,3.
16
©
Uit sin 60° =
© Noordhoff Uitgevers bv
0pm_MW9_VWO_3B-Uitw.indd 15
12, 3
12, 3
volgt WX =
dus WX ≈ 14,2.
WX
sin 60°
⁄
15
01-04-2009 16:36:32
er
sb
v
Hoofdstuk 7 Goniometrie
Uit sin 70° = h volgt h = 100 × sin 70° dus h ≈ 94,0 m.
100
De hoogte van de ballon is ongeveer 94 meter.
bDe loodlijn vanuit de ballon naar de grond verdeelt de gevraagde hoek in twee
hoeken: ∠A en ∠B.
∠A = 180° – 90° – 70° = 20°
94
cos ∠B = 120
∠B ≈ 38°
De gevraagde hoek is ongeveer 20° + 38° = 58°.
T-6a/b
D
C
47°
A
E
B
5 cm
Ui
tg
3 cm
ev
T-5a
c
d
Uit sin 47° = DE volgt DE = 3 × sin 47° dus DE ≈ 2,2 cm.
3
De oppervlakte is ongeveer 5 × 2,2 = 11 cm2.
e
Dat zijn ∠ADE of ∠EDA en ∠EDC of ∠CDE.
h volgt h = 3 × tan 14° dus h ≈ 0,75 m.
3
De hoogte van het schuurtje wordt 2 + 0,75 = 2,75 meter en dat is te hoog.
T-7Uit tan 14° =
©
No
or
dh
off
⁄
16
0pm_MW9_VWO_3B-Uitw.indd 16
© Noordhoff Uitgevers bv
01-04-2009 16:36:33