uitwerkingen opgaven les 15

VERON TWENTE ZENDCURSUS 2014 UITWERKINGEN OPGAVEN LES 15
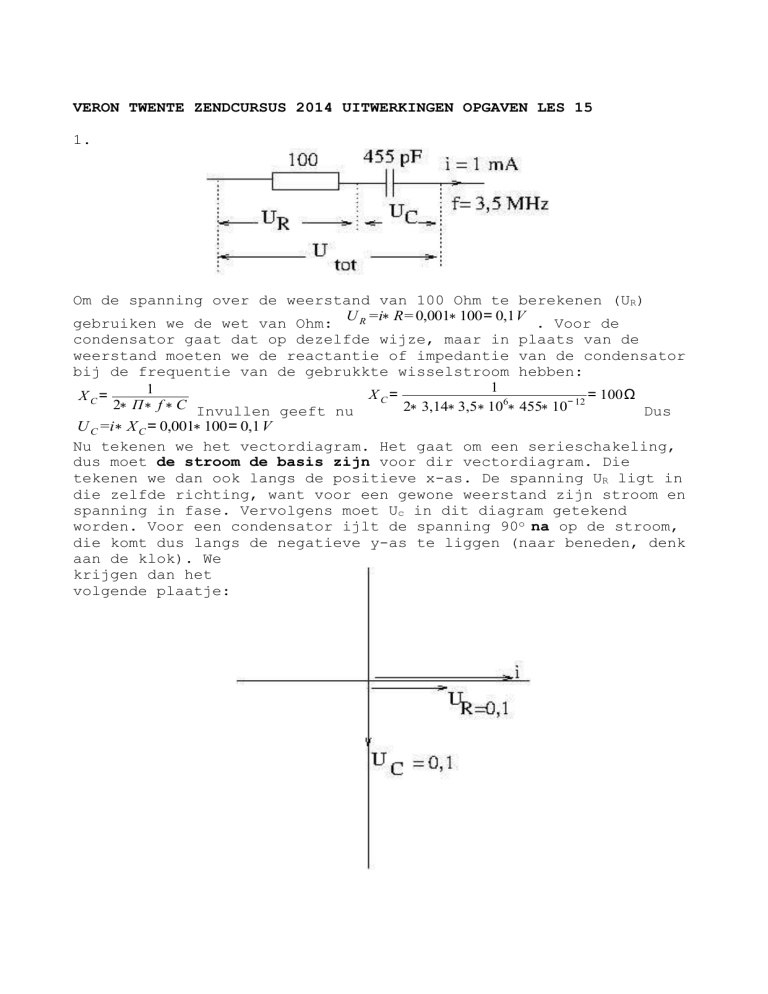
1.
Om de spanning over de weerstand van 100 Ohm te berekenen (UR)
U R =i∗ R= 0,001∗ 100= 0,1V
gebruiken we de wet van Ohm:
. Voor de
condensator gaat dat op dezelfde wijze, maar in plaats van de
weerstand moeten we de reactantie of impedantie van de condensator
bij de frequentie van de gebrukkte wisselstroom hebben:
1
1
XC=
= 100Ω
XC=
2∗ Π∗ f ∗ C Invullen geeft nu
2∗ 3,14∗ 3,5∗ 106∗ 455∗ 10− 12
Dus
U C =i∗ X C = 0,001∗ 100= 0,1 V
Nu tekenen we het vectordiagram. Het gaat om een serieschakeling,
dus moet de stroom de basis zijn voor dir vectordiagram. Die
tekenen we dan ook langs de positieve x-as. De spanning UR ligt in
die zelfde richting, want voor een gewone weerstand zijn stroom en
spanning in fase. Vervolgens moet Uc in dit diagram getekend
worden. Voor een condensator ijlt de spanning 90o na op de stroom,
die komt dus langs de negatieve y-as te liggen (naar beneden, denk
aan de klok). We
krijgen dan het
volgende plaatje:
Vervolgens gaan we de totale spanning bepalen als diagonaal in de
rechthoek
waarvan de twee
spanningen de
zijden zijn:
Van de driehoek, waarvan Utot de schuine zijde (hypothenusa) is,
zijn de rechthoekszijden evenlang. De fasehoek tussen de stroom
(die langs de positieve x-as lag) en de Utot is dus 45 graden.
Eventueel (maar hier niet gevraagd) kunnen we de Utot uitrekenen
met de stelling van Pythagoras.
2. We hebben weer de reactantie van de condensator nodig:
1
1
XC=
=
= 100 Ω
2∗ Π∗ f ∗ C 2∗ 3,14∗ 3,5∗ 10 6∗ 455∗ 10− 12
. We hebben nu te maken
met een parallelschakeling. De gemeenschappelijke basis is nu dus
de spanning van 10 V die over zowel de R als de C staat. Bij het
tekenen van het vectordiagram beginnen we dus met naar rechts op
de horizontale as de spanning te tekenen. Vervolgens tekenen we
daar de stroom door de weerstand van 100 Ohm ook langs (stroom en
spanning zijn in fase bij een gewone weerstand). De stroom door de
weerstand R is IR = 10/100 = 0,1 A. Vervolgens berekenen we de
stroom door de condensator
U 10
IC=
=
= 0,1 A
X C 100
De stroom door een condensator ijlt 90o voor op de
spanning en moeten we dus verticaal omhoog tekenen. De totale
stroom vinden we nu in het plaatje als de diagonaal in de
rechthoek gevormd door de twee stromen,
De totale stroom construeren we als de diagonaal in de rechthoek
gevormd door de twee stromen. De hoek die de totale stroom maakt
met de spanning (positieve x-as) is 45 graden omdat we te maken
hebben met een rechthoekige driehoek met twee gelijke zijden.
De stroom loopt dus 45
graden voor op de
aangelegde spanning.
3. We moeten nu allereerst de impedantie van de 4,55 uH spoel
utrekenen bij 3,5 MHz:
X L = 2∗ Π∗ f ∗ L= 2∗ 3,14∗ 3,5∗ 106∗ 4,55∗ 10− 6 = 100Ω . De spanningsval over
U R =I∗ R= 0,001∗ 100= 0,10V
R is dus
De spanningsval over L is
U L =i∗ X L= 0,001∗ 100= 0,1V
Bij het
tekenen
van het
vectord
iagram
nemen
we de
stroom
als
basis
(series
chakeli
ng) op
de horizontale as naar rechts. De spanning over de weerstand is
met die stroom in fase en moet dus ook horizontaal naar rechts
komen. Vervolgens moet de spanning over de spoel erin getekend
worden. Die ijlt 90 graden voor op de stroom en moet dus naar
boven wijzen. De totale spanning vinden we als de diagonaal in de
rechthoek gevormd door de twee aparte spanningen.
De hoek is weer 45 graden waarbij de spanning voor loopt
stroom.
4.
op de
We hebben weer de impedantie van de spoel van 4,55 uH bij 3,5 Mhz
nodig. Die hebben we al bij som 3 uitgerekend: 100 Ohm. De stroom
U 10
I R= =
= 0,1 A
R
100
door de weerstand is
. De stroom door de
zelfinductie van 4,55 uH is
U 10
I L=
=
= 0,1 A
X L 100
Bij het tekenen van het vectordiagram nemen de de
spanning als basis (parallelschakeling) en tekenen die naar rechts
langs de horizontale as. De stroom van 0,1 A door de weerstand
komt ook in diezelfde richting te liggen (stroom en spanning zijn
in fase bij een gewone weerstand). De stroom van de zelfinductie
ijlt 90 graden na op de spanning en komt dus verticaal naar
onderen te
liggen.
Het
vectordiag
ram wordt
dus:
De totale stroom ijlt nu 45 na op de spanning
5. het doel van een filterschakeling is het bevorderen van
gewenste signaalcomponenten en het verzwakken van ongewenste
signaal componenten.
6. Om te beginnen hebben we de reactanties van de L en de C bij
de verschillende frequenties nodig.
X L (1,75 MHz )= 2∗ Π∗ f ∗ L= 283,14∗ 1,75∗ 106∗ 4,55∗ 10− 6 = 50 Ω
X L (3,5 MHz )= 2∗ 3,14∗ 3,5∗ 106∗ 4,55∗ 10− 6 = 100 Ω
X L (7 MHz )= 2∗ 3,14∗ 3,5∗ 106∗ 4,55∗ 10− 6 = 200 Ω
1
1
=
= 200 Ω
2∗ Π∗ f ∗ C 2∗ 3,14∗ 1,75∗ 10 6∗ 455∗ 10− 12
1
X C (3,5 MHz )=
= 100 Ω
2∗ 3,14∗ 3,5∗ 10 6∗ 455∗ 10− 12
1
X C (7 MHz )=
= 50Ω
2∗ 3,14∗ 7∗ 106∗ 445∗ 10− 12
X C (1,75 MHz )=
We gaan nu de spanningen berekenen, allereerst voor als de
U L =I∗ X L = 50∗ 0,1= 5V
frequentie 1,75 MHz is.
. let op dat is de
U L (top )= √
2∗ 5= 7V
effectieve waarde. De
Deze spanning ijlt 90o voor
op de stroom (komt 90 eerder op de top). Voord de Uc vinden we
U C =I∗ X C = 0,1∗ 200= 20V .
2= 28 V Deze spanning
De topwaarde is dan 20∗ √
ijlt 90 na op de stroom. De top komt dus 90 graden later. We
krijgen nu de volgende figuur:
Voor de situatie bij 3,5 MHz krijgen we voor UL:
U L =I∗ X L = 0,1∗ 100= 10V
(effectief) dat is 14 V top.
U C =I∗ X C = 0,1∗ 100= 10 V
Voor Uc is dat
ook weer effectief dus ook 14 V topwaarde. De figuur wordt nu:
We zien dat de spanning Utot nu overal nul is!
De kring gedraagt zich als een kortsluiting voor 3,5 MHz
Voor de situatie bij 7MHz krijgen we voor
U L = I∗ X L = 200∗ 0,1= 20V effectief, dus 28 V topwaarde. Nu is
U C= I∗ X C= 0,1∗ 50= 5V (effectief) dus topwaarde = 7V. De figuur is nu:
De vectordiagrammen