hoofdstuk 1 Lenzen (inleiding)

hoofdstuk 5 Lenzen (inleiding).
5.1
Drie soorten lichtbundels
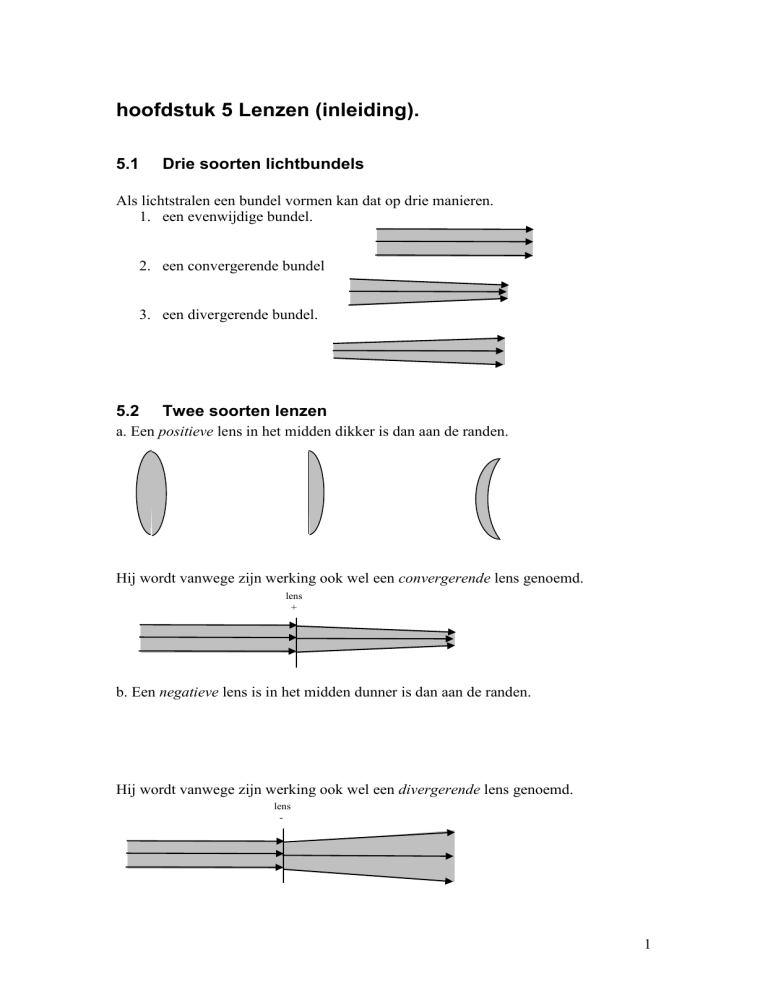
Als lichtstralen een bundel vormen kan dat op drie manieren.
1. een evenwijdige bundel.
2. een convergerende bundel
3. een divergerende bundel.
5.2
Twee soorten lenzen
a. Een positieve lens in het midden dikker is dan aan de randen.
Hij wordt vanwege zijn werking ook wel een convergerende lens genoemd.
lens
+
b. Een negatieve lens is in het midden dunner is dan aan de randen.
Hij wordt vanwege zijn werking ook wel een divergerende lens genoemd.
lens
-
1
5.3
Hoe werkt een lens? De brandpunten.
Bij het binnengaan van de lens wordt het licht naar de normaal toe gebroken;
bij het verlaten van de lens van de normaal af.
normaal
normaal
Hieronder zie je een evenwijdige lichtbundel. De bundel valt op een positieve lens.
Door de vorm van de lens komen alle lichtstralen in één punt bij elkaar.
De lichtbundel voor de lens was evenwijdig; dan heet dit snijpunt: het brandpunt.
Als symbool van brandpunt gebruiken we F (focus).
Elke lens heeft twee brandpunten:op gelijke afstand links en rechts van de lens (zie
hieronder). Je ziet ook wat wordt bedoeld met hoofdas en optisch middelpunt.
+
lens
2
5.4 Beeldvorming bij Lenzen.
Bij het gebruik van lenzen gaat het vaak om het maken van een beeld.
Als het beeld geprojecteerd kan worden noemen we het reëel.
Als een beeld niet geprojecteerd kan worden heet het virtueel.
Een reëel beeld kan je zien door naar het projectiescherm te kijken.
Een virtueel beeld kan je zien door in de lens te kijken.
De plaats van het beeld wordt aangegeven met de beeldafstand.(b).
De beeldafstand hangt af van de voorwerpsafstand (v) en de brandpuntsafstand (f).
In de figuur hieronder zie je hoe de drie afstanden zijn afgesproken.
Ook zie de voorwerpsgrootte (LL’)en de beeldgrootte(BB’).
+
lens
5.5 Waar komt het beeld (1)?
Tekenen: constructie.
Hieronder zie je een voorwerp. Het bestaat uit een lichtpunt L dat lichtstralen uitzendt.
L
3
Het beeld komt in het snijpunt van de drie constructielichtstralen.
I. De eerste loopt evenwijdig aan de hoofdas en gaat na de lens door F .
L
II. De tweede loopt door het optisch middelpunt van de lens en gaat gewoon
rechtdoor.
L
III. De derde is de omgekeerde van de eerste hij loopt voor de lens door F na de lens
evenwijdig aan de hoofdas.
L
Alle drie: Het snijpunt noemen we B, het beeld van L.
L
B
Betekenis: Alle lichtstralen die vanuit L door de lens lopen gaan door B.
4
5.6 De sterkte van een lens.
Een sterke positieve lens is een lens die een evenwijdige bundel licht vlak bij de lens
bij elkaar brengt. De brandpuntsafstand is dus klein.
+
Ook aan de vorm kan je zien dat een lens sterk is; hij is erg bol.
De sterkte van de lens bereken je uit de brandpuntsafstand met de volgende formule:
1
S
( Dpt , dioptrie )
f
Hierbij moet f in meters (m) worden opgegeven.
Een negatieve lens heeft een negatieve brandpuntsafstand en dus ook een negatieve
sterkte. Denk maar aan brillenglazen.
5
5.8 Waar komt het beeld(2)?
De lenzenformule.
De samenhang tussen v, b en f ligt vast in de lenzenformule
1 1 1
 
v b f
De formule kan ook worden geschreven in de vormen
f 
vb
vb
b
vf
v f
v
bf
b f
Voorbeeld: Een lens heeft brandpuntsafstand: 3,0 cm.
Een voorwerp staat 5,0 cm van de lens af.
Bereken de beeldafstand.
5 * 3 15

5-3 2
b  7,5 cm
b
5.9 Een virtueel beeld.
Je kunt met een positieve lens een virtueel beeld krijgen. Dit gebeurt als de
voorwerpsafstand kleiner is dan de brandpuntsafstand (v < f)
Het beeld komt aan de zelfde kant van de lens als het voorwerp. Je moet het beeld
stippelen; het is virtueel. Je kan het beeld zien als je vanaf rechts in de lens kijkt.
a. tekenen
+
+
6
b. rekenen.
voorbeeld:
v = 3,0 cm,
bereken b.
f = 4,0 cm (let op: v < f)
3 * 4 12

3  4 1
b  12 cm
b
b is negatief! Hieraan zie je dat het een virtueel beeld is.
5.10 Lineaire vergroting Nlin.
Met lineaire vergroting wordt
bedoeld: hoeveel maal is het beeld
langer dan het voorwerp.
De formule wordt dus:
BB '
LL'
Dus beeldgrootte gedeeld door voorwerpsgrootte.
Nlin kan kleiner dan 1 zijn; dan is het beeld verkleind.
N lin 
De lineaire vergroting is te berekenen uit v (voorwerpsafstand) en b (beeldafstand)
met:
N lin 
b
v
De strepen worden absoluutstrepen genoemd. Ze zorgen ervoor dat het resultaat van
de berekening altijd positief (of 0) wordt.
voorbeeld:
v = 4,0 cm b = -12 cm.
N lin 
 12
 3  3
4
De absolute waarde van –3 is 3
Het beeld is drie maal zo groot als het voorwerp.
7
Hoofdstuk6. Toepassing van positieve lenzen.
6.1 De camera.
In een camera wordt een reëel, verkleind omgekeerd beeld geprojecteerd op een film
of op een chip. Door de lens naar voor en achteren te schuiven ontstaat een scherp
beeld. Onscherp houdt in: L’ wordt niet afgebeeld in een punt maar in een vlakje.
De lichthoeveelheid wordt geregeld met een diafragma. Het diafragma dekt de lens
gedeeltelijk af.
L’
L
B
B’
6.2 Het oog; gezichtshoek.
Net als de camera maakt het oog
een reëel, verkleind omgekeerd
beeld.
Dit beeld wordt op het netvlies
gevormd. De iris wekt als
diafragma. De opening in de iris
heet pupil.
De lens heeft een variabele
brandpuntsafstand.
Scherpstellen
Het scherpstellen wordt accommoderen genoemd.
Een ongeaccommodeerd oog is een ontspannen oog. De brandpuntsafstand van de
ooglens is dan maximaal. Je kunt met ongeaccommodeerd oog kijken naar
ververwijderde voorwerpen.
Als het beeld precies op het netvlies wordt geprojecteerd zie je het scherp.
De nabijheidafstand
Als je van een voorwerp meer details wil zien, breng je het dichter naar je oog toe.
Er is echter een minimale gezichtsafstand: de nabijheidafstand (n).
Als een voorwerp in het nabijheidpunt staat moet je maximaal accommoderen.
Als v kleiner is dan n kan je het voorwerp niet scherp zien.
In dat geval kan een vergrootglas (loep) helpen.
8
Gezichtshoek
Het is onmogelijk om de grootte van het beeld in het oog op te meten.
Daarom werken we meestal het de gezichtshoek.
In de figuur hieronder zie je wat er met gezichtshoek ( , alpha)wordt bedoeld:
De hoek tussen de bovenste en de onderste lichtstraal waarmee het oog het voorwerp
ziet..
De gezichtshoek kan berekend worden met tan =LL’/v
Het beeld op het netvlies is omgekeerd.
netvlies
We zijn hieraan gewend; we “zien” het rechtop.
.
Hoekvergroting.
Door een optisch instrument te gebruiken kan de gezichtshoek worden vergroot.
Bijvoorbeeld met een vergrootglas (loep) of een microscoop. Het gezichtshoek met
instrument noemen we  (bèta).
De hoekvergoting (Nang) is dan :

N ang 

Hoe groter de gezichtshoek, hoe groter het netvliesoppervlak dat het beeld bestrijkt.
Je kunt dan veel details zien.
6.3 de loep, blik op oneindig….
Onze ogen worden het minst moe als ze in de verte kijken.
Bij het gebruik van een vergrootglas (loep) zorgen we er dus voor dat het beeld in het
oneindige komt.
Dit krijg je als je het voorwerp in het brandpunt zet.
Alle lichtstralen die vanuit L’ door de lens gaan lopen dan evenwijdig aan elkaar.
De stralengang wordt :
+
L’
L=F
F
9
Bij benadering is de hoekvergroting Nangvan een loep gelijk aan
N ang 
n
f loep
n:
floep:
6.4 de microscoop (bij ongeaccommodeerd oog)
Een eenvoudige microscoop bestaat uit twee lenzen :
 het objectief aan de kant van het voorwerpje
 het oculair aan de kant van je oog
Het objectief zorgt voor een lineaire vergroting
Formules:
1
1
1


vobj bobj
f obj
N lin,obj 
bobj
vobj
Het objectief vormt een vergroot reëel omgekeerd beeld. Dit beeld BB’ staat in het brandpunt
van het oculair.
Het oculair werkt als een loep en zorgt voor een hoekvergroting
N ang,oc 
n
f oc
De hoekvergroting van de microscoop:
N ang,micr  N lin, obj  N ang,oc
afstand van objectief. tot oculair :
bobj  f oc
Deze afstand wordt de tubuslengte genoemd
10
11
oefensommen hoofdstuk 5
5.1.1
Hieronder zie je vier lichtbundels. Hoe worden ze genoemd?
1:
2:
3:
4:
1
2
a
3
b
4
c
5.2.1
Hierboven zie je drie lenzen.
Hoe worden ze genoemd?
a.
b.
c.
5.3.1
Van een positieve lens zijn de brandpunten gegeven.Teken hoe de lichtbundel door de
lens gaat.
12
5.3.2
F
Van welke lens is F het brandpunt?
a. Van de linker lens.
b. Van de rechter lens.
c. Van beide lenzen.
d. Van geen van beide lenzen.
5.4.1
Hieronder zie je een lens met links een voorwerp.
Geef in de figuur aan: v, b, f, O, F, LL’, BB’ en de hoofdas.
+
lens
5.5.2
Hierboven zie je een lens met links een voorwerp. Controleer of het beeld op de juiste
plaats staat door drie constructielichtstralen te tekenen.
5.5.3
Een voorwerp van 0,8 cm groot staat op de hoofdas van een lens (f= +2,0 cm).
De afstand van voorwerp tot lens bedraagt 3,5 cm.
Teken de drie constructielichtstralen om te zien waar het beeld komt.
Meet de beeldgrootte op.
13
5.5.4
Een voorwerp van 0,8 cm groot staat op de hoofdas van een lens (f= +4,0 cm).
De afstand van voorwerp tot lens bedraagt 2,5 cm.
Teken de drie constructielichtstralen om te zien waar het beeld komt.
Meet de beeldgrootte op.
5.7.1
De brandpuntsafstand van een lens is 1,5 m. Bereken de sterkte.
5.7.2.
De brandpuntsafstand van een lens is -20 cm. Bereken de sterkte.
5.7.3.
De sterkte van een lens is 4,0 dpt. Bereken de brandpuntsafstand in cm.
5.7.4.
De sterkte van een lens is -11 dpt. Bereken de brandpuntsafstand in cm.
5.7.5.
+
Bepaal door opmeten de sterkte van de lens in de figuur hierboven.
14
5.8.1
S
1
(Dpt, dioptrie )
f
f 
vb
vb
b
vf
v f
Hieronder zie je een tabel.
Vul deze verder in.
v (cm)
b (cm)
6
10
v
bf
b f
f (cm)
S (dpt)
2
30
15
5
10
4
5.10.1
Een voorwerp is 3,5 cm lang en staat loodrecht op de hoofdas op 6,0 cm van een lens
waarvan de sterkte 10 dpt is.
a. Bereken de brandpuntsafstand van de lens. Geef je antwoord in cm.
b. Bereken de beeldafstand, de vergroting en beeldgrootte.
c. Teken op ruitjespapier de lens, de brandpunten het voorwerp het beeld
15