Grafieken, functies en verzamelingen Eerst enkele begrippen

Grafieken, functies en verzamelingen
Eerst enkele begrippen
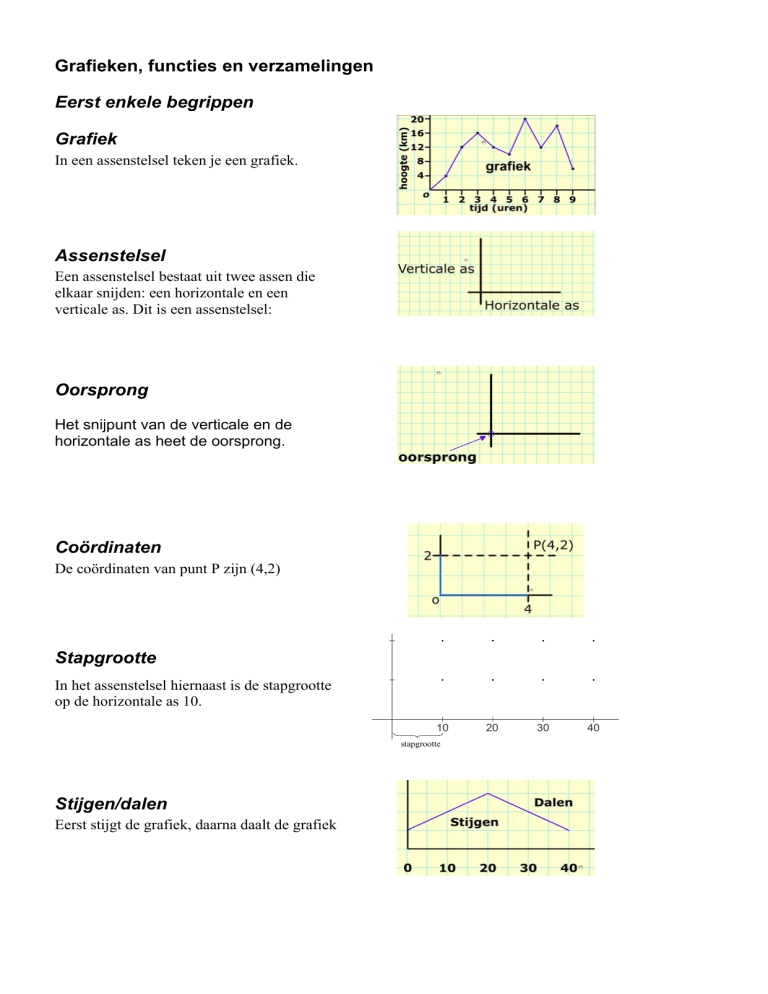
Grafiek
In een assenstelsel teken je een grafiek.
Assenstelsel
Een assenstelsel bestaat uit twee assen die
elkaar snijden: een horizontale en een
verticale as. Dit is een assenstelsel:
Oorsprong
Het snijpunt van de verticale en de
horizontale as heet de oorsprong.
Coördinaten
De coördinaten van punt P zijn (4,2)
Stapgrootte
In het assenstelsel hiernaast is de stapgrootte
op de horizontale as 10.
10
stapgrootte
Stijgen/dalen
Eerst stijgt de grafiek, daarna daalt de grafiek
20
30
40
Constant
De grafiek daalt niet en stijgt niet, de grafiek
is constant.
Steil
De grafiek stijgt eerst langzaam en dan snel.
De grafiek gaat dan steiler.
Zaagtand/scheurlijn
Verband
In de grafiek zie je het verband tussen de
leeftijd en de lengte van mensen: kinderen
groeien. Ze worden steeds een beetje langer.
lengte
Wanneer je het onderste stukje van de
verticale as weglaat, teken je een zaagtand (of
scheurlijn).
leeftijd
Tabel
In een tabel staan gegevens overzichtelijk bij
elkaar. Dit is een tabel:
Grafieken
ruitjespapier
(het)
roosterpapier
roosterlijn
roosterpunt
assenstelsel (het)
x-as (de) en y-as
schaalverdeling
(de)
oorsprong (de)
x-coördinaat (de)
x-waarde (de)
y-waarde (de)
kwadrant (het)
grafiek (de)
uitzetten tegen
Hiernaast is op ruitjespapier ( of:
roosterpapier) getekend.
Het roosterpapier bestaat uit
roosterlijnen ( horizontaal en
verticaal) en roosterpunten.
Er is op het roosterpapier een
assenstelsel getekend zoals wij dat in
de wiskunde vaak doen.
Het assenstelsel bestaat uit een
horizontale as ( vaak de x-as
genoemd) en daar loodrecht op een
verticale as ( vaak de y-as genoemd).
Verder geef je op de assen een
schaalverdeling aan.
Bij het snijpunt van de assen zetten we een O van oorsprong.
Met dit assenstelsel kunnen we nu elk punt van het vlak aangeven ( zie de
voorbeelden in de tekening).
Bijv.: (4,2) is het punt met x-coördinaat 4 en y-coördinaat 2;
je vindt dit punt door vanuit de oorsprong 4 naar rechts en 2 naar boven te gaan.
en: (-2,-3) vind je door vanuit de oorsprong 2 naar links te gaan en 3 naar
beneden.
Op de x-as is de y-waarde altijd 0 en op de y-as is de x-waarde altijd 0.
Tenslotte: door het assenstelsel wordt het vlak in vier delen verdeeld:de
kwadranten. We benoemen de kwadranten tegen de klok in, rechtsboven
beginnend: het eerste, tweede, derde en vierde kwadrant.
In zo'n assenstelsel tekenen we vaak grafieken.
Zo is bijvoorbeeld in het voorbeeld
hiernaast de grafiek getekend waarin
de lengte van een meisje is uitgezet
tegen haar leeftijd.
Let op dat de schaalverdeling van de
horizontale en verticale as nu niet
meer dezelfde is!
De getekende lijn noemen we de
lengte-grafiek.
Zo ligt op die grafiek het punt
(7,110).
De betekenis is duidelijk: toen het
meisje 7 was, was haar lengte 110
cm.
Functies
Meer wiskundig zeggen we:
óf:
óf:
aan 7 wordt 110 gekoppeld
aan 7 wordt 110 toegevoegd
bij 7 hoort 110.
We noteren wel:
7  110
uitspraak:
7 wordt 110
( of één van de uitspraken hierboven)
óf:
L(7) = 110
uitspraak:
beeld (het)
origineel (het)
de L van 7 is 110
( waarbij de L staat voor: de lengte)
We noemen 7 een origineel en 110 het bijbehorende beeld.
Zo geldt bijvoorbeeld ook:
het beeld van 9 is 120 (notaties: L(9) = 120 of 9  120 )
én:
het origineel van 100 is 5.
domein (het)
bereik (het)
functie (de)
Alle originelen bij elkaar ( hier 1 t/m 18) heten:
het domein (vaak: D)
Alle beelden bij elkaar ( hier 75 t/m 165) heten:
het bereik (vaak: B)
We hebben hier een voorbeeld van wat in de wiskunde een FUNCTIE genoemd
wordt ( aan elk origineel wordt precies één beeld gekoppeld).
Een meer wiskundig voorbeeld:
tabel (de)
visgraattabel
Elk vierkant heeft een oppervlakte.
je kunt de volgende tabel maken :
Lengte
½
1
1½
2
2½
3
3½
4
oppervlakte
¼
1
2¼
4
6¼
9
12¼
16
Zo'n tabel noemen we een visgraattabel.
Ook hier weer bijvoorbeeld:
3  9
Algemener:
functievoorschrift
(het)
l  l2
Dit heet het functievoorschrift.
Ook noteren we :
O:l l2
O(l)=l2
de O van l is l-kwadraat.
(O staat voor oppervlakte en l voor lengte)
én ook:
uitspraak:
De grafiek:
y-as of Opp -as
1
O
1
x-as of l-as
In de wiskunde zullen we de originelen vaak met x en de beelden vaak met y
aangeven ( zoals ook de horizontale as meestal x-as en de verticale as meestal yas genoemd wordt); ook geven we functies vaak aan met een f.
Zo krijg je dan:
f: x x2
of:
of:
f(x) = x 2
y = x2
In onze grafiek vind je zo het domein op de x-as ( zie de stippellijnen):
D=[1,4]
en het bereik vind je op de y-as:
B = [ 1 , 16 ]
Hierbij hebben we gebruik gemaakt van de zogenaamde interval-notatie.
Verzamelingen en intervallen
gesloten interval
(het)
getallenlijn (de)
-4
-3
-2
-1
0
1
2
3
4
-4
-3
-2
-1
0
1
2
3
4
open interval
oneindig interval
verzameling (de)
-4
-3
-2
-1
0
1
2
3
4
-4
-3
-2
-1
0
1
2
3
4
[1, 4] heet een gesloten interval; we
bedoelen hiermee alle getallen tussen
1 en 4 met de grenzen 1 en 4 erbij.
Vaak wordt dat op de getallenlijn
zoals hiernaast aangegeven: de dichte
punten bij 1 en 4 geven aan dat deze
grenzen erbij horen.
Hiernaast is een open interval
getekend.
Notatie:
 3,2
we bedoelen hiermee alle getallen
tussen -3 en 2 maar nu zonder
degrensgetallen -3 en 2. Op de
getallenlijn wordt dat zoals hiernaast
aangegeven: de open punten bij -3 en
2 geven aan dat deze grenzen er niet
bij horen.
Tenslotte heb je nog de oneindige
intervallen:
vb:
alle getallen groter dan of gelijk aan 1
Notatie:
1, 
en
alle getallen kleiner dan 2
Notatie:
, 2
Voor al deze intervallen is er ook nog de op de Nederlandse scholen niet meer
veel gebruikte verzamelingnotatie:
( hierin betekent “ x | ” : al die x-en waarvoor gedlt )
1 , 4   x | 1  x  4
 3 , 2  x | 3  x  2
 , 2  x | x  2
 1 ,   x | x  1
Uitspraak: alle x-en groter of gelijk
aan 1 én kleiner of gelijk aan 4
Er bestaan natuurlijk ook half-open - half-gesloten intervallen:
1, 3
 x | 1  x  3
getallenverzamelingen
natuurlijke
getallen
gehele getallen
rationale getallen
reële getallen
irrationaal
Al deze intervallen zijn (aaneengesloten delen) van de verzameling van de reële
getallen.
De bekende getallenverzamelingen zijn:
N = { 0 , 1, 2, 3, 4 , …. }
de verzameling van de natuurlijke getallen
Z = { …. , -3 , -2 , -1 , 0 , 1 , 2 , 3 , …… }
de verzameling van de gehele getallen
Q = { …. , -3 , -1 , 0 , 1 , 5, 12 , 2 13 …… }
de verzameling van de rationale getallen
( de gehele getallen maar ook de gebroken getallen)
R = { …. , -3 , -1 , 0 , 1 , 5, 12 , 2 13 , √2 ,  ,…… }
de verzameling van de reële getallen;
( de rationale getallen en de irrationale getallen)
Bijvoorbeeld √2 is irrationaal omdat zij niet als een gebroken getal geschreven
kan worden.
Alle getallen van R worden vaak op een rechte lijn ‘gedacht’, de getallenlijn:
-4
even
oneven
priemgetallen
vijfvoud (de)
veelvoud
-3
-2
-1
0
1
2
3
4
Terug naar de natuurlijke getallen; we onderscheiden nog:
2,4,6,8,10 ,……
zijn de even getallen
1,3,5,7,9,11,13 ,… zijn de oneven getallen
1,3,5,7,11,13,17, … zijn de priemgetallen
( de getallen die alleen door 1 en zichzelf deelbaar zijn)
5, 10,15,20,25,…… zijn de vijfvouden of ook: veelvouden van 5
Typen grafieken
lijngrafiek
diagram (het)
statistiek (de)
staafdiagram
(het)
frequentie (de)
Naast de bovenstaande lijngrafieken bestaan er ook nog vele andere soorten
grafieken of diagrammen. Vooral in de statistiek worden deze andere soorten veel
gebruikt.
We benoemen er een aantal:
Dit staafdiagram laat zien hoeveel
werknemers van een bepaald bedrijf
met welk soort vervoer naar hun werk
komen. Je noemt dat de frequenties.
ov: openbaar vervoer
f: fiets
a:auto
v: voetganger
Dezelfde gegevens als in het vorige
voorbeeld zijn nu in een
cirkeldiagram weergegeven.
cirkeldiagram
(het)
Het histogram. De staafjes van het
histogram worden aaneengesloten
getekend.
vb:
er zijn 6 werknemers die 4 keer
per week sporten
histogram (het)
aaneengesloten
Een stapeldiagram of een
samengesteld staafdiagram
vb:
van de 9 werknemers, die met
openbaar vervoer naar hun werk
komen zijn er 2 laag, 3
middelbaar en 4 hoog opgeleid
stapeldiagram
(het)
óf:
samengesteld
staafdiagram
Toenamendiagram
toenamendiagram
We kunnen van de lengte-grafiek van het meisje op pagina 3 een zogenaamde
toenamendiagram maken. Eerst maken we daarvoor een tabel van de grafiek:
De tabel:
Leeftijd
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Hiermee kan je de toenamentabel maken:
Lengte
?
74
84
90
94
100
104
110
114
120
124
130
135
141
150
159
165
165
165
de toenamen
+?
+10
+6
+4
+6
interval
[0,1]
[1,2]
[2,3]
[3,4]
[4,5]
[5,6]
[6,7]
[7,8]
[8,9]
[9,10]
[10,11]
[11,12]
[12,13]
[13,14]
[14,15]
[15,16]
[16,17]
[17,18]
toename
?
10
6
4
6
4
6
4
6
4
6
5
6
9
9
6
0
0
Nu kunnen we het toenamendiagram tekenen, door boven elk interval een staafje
te tekenen met als hoogte de toename over dat interval:
Minder inzichtelijk maar zeker zo gangbaar is de volgende vorm, waarbij de
toenames als punten met verticale lijnstukjes boven de rechtergrenzen worden
gezet:
Je kunt de ‘stapgrootte’ van het toenamendiagram veranderen. Bijvoorbeeld
bekijk je niet de toename per jaar, maar per twee jaar. De lengte van de
tijdsintervallen worden dan dus twee jaar in plaats van één jaar.
Als we vragen wat de gemiddelde groeisnelheid is van het meisje van haar 10e tot
haar 16e verjaardag, weet je vast wel wat je moet uitrekenen:
per jaar
differentiequotiënt
differentie (de)
165  124 41

 6,8 cm/jaar (Uitspraak: centimeter per jaar).
16  10
6
In de wiskunde noemen we dit een differentiequotiënt, een quotiënt van
differenties ofwel een deling van verschillen: we delen het verschil in lengtes door
het verschil in leeftijd. We noteren:
lengte 165  124 41


 6,8 cm/jaar
leeftijd
16  10
6
( Δ (de Griekse letter delta) staat voor differentie en dat betekent dus
verschil)
We zeggen dat het differentiequotiënt is berekend over het tijdsinterval [10 , 16] .