INLEIDING FUNCTIES 1. COÖRDINATEN

INLEIDING FUNCTIES
1. COÖRDINATEN...........................................................................................................................1
2. FUNCTIES...................................................................................................................................2
3. ARGUMENT EN BEELD..............................................................................................................3
4. HET FUNCTIEVOORSCHRIFT....................................................................................................4
5. DE FUNCTIEWAARDETABEL.....................................................................................................5
6. DE GRAFIEK................................................................................................................................6
7. FUNCTIES HERKENNEN............................................................................................................7
8. OPLOSSINGEN...........................................................................................................................9
1. COÖRDINATEN
Als je punten op een assenstelsel zet, kan je voor elk punt een coördinaat geven.
Het eerste coördinaatgetal lees je af op de x-as.
Het tweede coördinaatgetal lees je af op de y-as.
Maak de oefeningen hieronder en het wordt duidelijk!
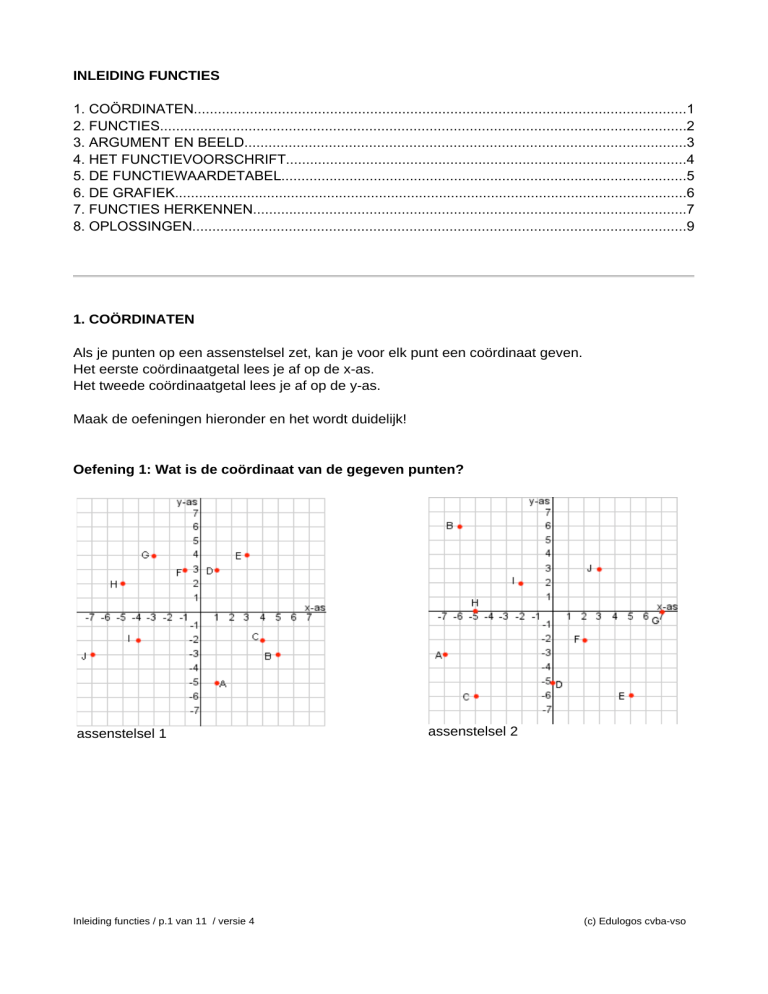
Oefening 1: Wat is de coördinaat van de gegeven punten?
assenstelsel 1
Inleiding functies / p.1 van 11 / versie 4
assenstelsel 2
(c) Edulogos cvba-vso
REËLE FUNCTIES BESPREKEN
1. DOMEIN.......................................................................................................................................1
2. BEREIK........................................................................................................................................3
3. NULWAARDEN EN NULPUNTEN...............................................................................................3
4. HET TEKENVERLOOP................................................................................................................5
5. FUNCTIEVERLOOP (STIJGEN, DALEN EN EXTREMA)............................................................7
6. SYMMETRIE................................................................................................................................8
7. BUIGPUNTEN............................................................................................................................11
8. PERIODICITEIT.........................................................................................................................13
9. ASYMPTOTEN...........................................................................................................................13
10. DE SOORTEN REËLE FUNCTIES EN HUN KENMERKEN....................................................16
10.1. VEELTERMFUNCTIES.....................................................................................................16
10.2. RATIONALE FUNCTIES...................................................................................................19
10.3. EXPONENTIËLE FUNCTIE..............................................................................................22
10.4. LOGARITMISCHE FUNCTIE............................................................................................23
10.5. IRRATIONALE FUNCTIES...............................................................................................24
10.6. GONIOMETRISCHE FUNCTIE........................................................................................25
11. OEFENINGEN..........................................................................................................................29
12. OPLOSSINGEN.......................................................................................................................33
1. DOMEIN
notatie: dom f (lezen als ‘het domein van de functie’).
Om een koppel te vinden, vervang je de x door een getal. De verzameling van alle getallen die
daarvoor in aanmerking komen, is het domein van de functie.
f: y = x + 2
• Je kan x vervangen door om het even welk reëel getal. Er ontstaat nooit een probleem bij de
berekening van het beeld.
• Het domein is gelijk aan alle reële getallen → dom f = ℝ
6
x
• De noemer van een breuk mag nooit 0 zijn. Je kan x in dit geval niet vervangen door 0, want dan
kom je 0 uit in de noemer. Alle andere reële getallen kunnen wel.
• Het domein is gelijk aan alle reële getallen behalve 0 → dom f = ℝ 0
f : y=
f : y= x
• Het getal onder een wortelteken mag niet negatief zijn (0 mag wel). Je kan x dus alleen
vervangen door een positief reëel getal.
• Het domein is gelijk aan alle positieve reële getallen → dom f = ℝ +
Functies bespreken / p.1 van 35 / versie 1
© Edulogos cvba-vso
EERSTEGRAADSFUNCTIES
1. INLEIDING...................................................................................................................................1
2. GRAFIEK VAN EEN EERSTEGRAADSFUNCTIE.......................................................................1
3. DOMEIN EN BEREIK VAN EEN EERSTEGRAADSFUNCTIE.....................................................3
4. NULWAARDE VAN EEN EERSTEGRAADSFUNCTIE................................................................3
5. TEKENVERLOOP VAN EEN EERSTEGRAADSFUNCTIE..........................................................4
6. MAXIMUM EN MINIMUM.............................................................................................................4
7. SYMMETRIE................................................................................................................................4
8. DIFFERENTIEQUOTIËNT VAN EEN EERSTEGRAADSFUNCTIE.............................................5
9. HET VOORSCHRIFT VAN EEN EERSTEGRAADSFUNCTIE BEPALEN....................................6
10. OEFENINGEN............................................................................................................................7
11. OPLOSSINGEN.......................................................................................................................11
1. INLEIDING
Wanneer het voorschrift van een functie een onbekende (x) bevat en de macht van x is maximaal
1 (= eerste graad), dan spreken we van een eerstegraadsfunctie.
Het voorschrift van een eerstegraadsfunctie is altijd y = ax + b.
We noemen "y = ax + b" de standaardvorm van een eerstegraadsfunctie.
a kan om het even welk reëel getal zijn behalve 0.
b kan om het even welk reëel getal zijn (dus ook 0)
voorbeelden:
y = 3x – 5
y = -2,83 + 1,9
y=x–3
y = 2x
a=3
a = -2,83
a=1
a=2
b = -5
b = 1,9
b = -3
b=0
2. GRAFIEK VAN EEN EERSTEGRAADSFUNCTIE
De grafiek van een eerstegraadsfunctie is altijd een schuine rechte.
Geval 1: y = ax
De grafiek is een schuine rechte die door de oorsprong O van het assenstelsel gaat.
Om de grafiek te tekenen volstaat het dus de coördinaat van 1 willekeurig punt te kiezen. Om een
schuine rechte te tekenen, heb je genoeg aan twee punten. Het eerste punt reken je uit door x te
vervangen door een willekeurig reëel getal. Het tweede punt is de oorsprong.
Eerstegraadsfuncties / p.1 van 12 / versie 5
© Edulogos cvba-vso
TWEEDEGRAADSFUNCTIES
1. DEFINITIE....................................................................................................................................1
2. GRAFIEK VAN EEN TWEEDEGRAADSFUNCTIE......................................................................1
3. KENMERKEN VAN TWEEDEGRAADSFUNCTIES.....................................................................3
4. GRAFIEK VAN EEN TWEEDEGRAADSFUNCTIE TEKENEN ZONDER GRM...........................8
5. OEFENINGEN..............................................................................................................................9
6. OPLOSSINGEN.........................................................................................................................14
1. DEFINITIE
Een tweedegraadsfunctie is een veeltermfunctie die een tweedegraadsvergelijking als voorschrift
heeft. Met andere woorden: het voorschrift is (na uitwerken en/of herleiden) een veelterm met een
x2 en geen term met een groter macht.
Een tweedegraadsfunctie heeft de standaardvorm: y = ax2 + bx + c
Daarbij geldt dat a nooit gelijk kan zijn aan 0 (b en c wel). Immers: als a = 0 dan wordt het
voorschrift y = bx + c en dan hebben we niet meer te maken met een tweedegraadsfunctie.
Een tweedegraadsfunctie kan vier vormen hebben:
• f : y = ax 2 + bx + c
• f : y = ax2  0x  0 → f : y = ax 2
• f : y = ax2  bx  0 → f : y = ax 2  bx
• f : y = ax2  0x  c → f : y = ax 2  c
Een andere naam voor tweedegraadsfuncties is kwadratische functies.
2. GRAFIEK VAN EEN TWEEDEGRAADSFUNCTIE
De grafiek van een tweedegraadsfunctie is altijd een parabool.
Kenmerken van een parabool:
• u-vorm
• gewone u → dit noemen we een dalparabool
• omgekeerde u → dit noemen we een bergparabool
• het is altijd mogelijk om een symmetrie-as te tekenen
Het snijpunt van de grafiek en de symmetrie-as, is de top van de parabool.
Tweedegraadsfuncties / p.1 van 16 / versie 4
TWEEDEGRAADSVERGELIJKINGEN
1. OPLOSSEN VAN TWEEDEGRAADSVERGELIJKINGEN
Dit moet je zeker kunnen. Maak oefeningen tot je dit zonder problemen kan.
1.1. TYPE ax2 + bx = 0
Methode:
stap 1: ontbinden in factoren door x (en eventueel een getal) buiten de haakjes te brengen
Je houdt over x (veelterm van de eerste graad)
stap 2: veelterm van de eerste graad gelijkstellen aan 0 en de eerstegraadsvergelijking oplossen.
Oplossing: 0 en oplossing van de eerstegraadsvergelijking
Voorbeelden:
1) 3x 2 +2x = 0
stap 1: x (3x + 2) = 0
2) −3x 2 + 9x = 0
stap 1: -3x (x – 3) = 0
stap 2: 3x + 2 = 0
x = -2/3
stap 2: x – 3 = 0
x=3
oplossing: 0 en -2/3
oplossing: 0 en 3
Oefening: los op
opgave
2
1) x +8x =0
2) x2 – 5x = 0
3) 3x 2 +6x =0
4) 3x 2 +15x = 0
5) 7x 2 +35 = 0
6) 7x 2 – 56x =0
7) 4x 2 – 7x = 0
8) −5x 2 + x = 0
9) 8x 2 – 7x = 0
10) −5x 2 – 3x =0
Tweedegraadsvergelijkingen / p.1 van 13 / versie 1
oplossing(en)
VEELTERMFUNCTIES
1. WAT IS EEN VEELTERMFUNCTIE?...........................................................................................1
2. BESPREKEN VAN EEN VEELTERMFUNCTIES VAN DE DERDE GRAAD OF HOGER............1
3. OEFENINGEN..............................................................................................................................3
4. OPLOSSINGEN...........................................................................................................................4
1. WAT IS EEN VEELTERMFUNCTIE?
Een veeltermfunctie is een reële functie die een veelterm in x (= een veelterm met minstens 1 x)
als voorschrift heeft.
De grootste exponent die voorkomt in de veelterm (na uitwerken en herleiden), bepaalt de graad
van de functie.
Voorbeelden:
f: y = x - 5
f: y = x² - 5x + 3
f: y = x³ + 6x² + 5
f: y = x4 - 8
f: y = (x3 – 2)2
grootste exponent = 1 → eerstegraadsfunctie
grootste exponent = 2 → tweedegraadsfunctie
grootste exponent = 3 → derdegraadsfunctie
grootste exponent = 4 → vierdegraadsfunctie
grootste exponent = 6 → zesdegraadsfunctie
Eerstegraadsfuncties → zie hoofdstuk eerstegraadsfuncties
Tweedegraadsfuncties → zie hoofdstuk tweedegraadsfuncties
Opgaven in verband met eerste- en tweedegraadsfuncties kan je bij voorkeur zonder rekenmachine oplossen. Voor opgaven met derdegraadsfuncties (of hogere graad) gebruik je de TI.
2. BESPREKEN VAN EEN VEELTERMFUNCTIES VAN DE DERDE GRAAD OF HOGER
Functiewaardetabel
Zoek met de TI het beeld van enkele willekeurige waarden. bv. f(1), f(0),... of roep de
functiewaardetabel op. (probeer de beelden ook zelf te berekenen)
Noteer de waarden en hun beeld in een tabel.
Grafiek
Met TI.
Domein en bereik
Domein altijd ℝ .
Bereik → aflezen op de grafiek.
Veeltermfuncties / versie 5b / p.1 van 10
EXPONENTIËLE FUNCTIES
1. DE EXPONENTIËLE FUNCTIE....................................................................................................1
1.1. ALGEMENE VORM..............................................................................................................1
1.2. ANDERE VORMEN..............................................................................................................2
2. EXPONENTIËLE VERBANDEN...................................................................................................3
2.1. EXPONENTIËLE GROEI......................................................................................................3
2.2. EXPONENTIËLE DALING....................................................................................................5
2.3. EXPONENTIËLE GROEI EN DALING ONDERSCHEIDEN..................................................7
2.4. DE GROEIFACTOR AANPASSEN.......................................................................................7
2.5. GEGEVENS AFLEIDEN UIT EEN FUNCTIEWAARDETABEL.............................................8
2.6. OEFENINGEN......................................................................................................................9
3. LINEAIRE EN EXPONENTIËLE GROEI OF DALING................................................................14
3.1. LINEAIR VS. EXPONENTIEEL...........................................................................................14
3.2. DE GRAFIEK VAN EEN LINEAIRE GROEI / DALING........................................................16
3.3. DE GRAFIEK VAN EEN EXPONENTIËLE GROEI / DALING ............................................17
3.4. TOEPASSING: ENKELVOUDIGE EN MEERVOUDIGE INTREST.....................................19
3.5. OEFENINGEN ...................................................................................................................20
4. OPLOSSINGEN.........................................................................................................................21
1. DE EXPONENTIËLE FUNCTIE
1.1. ALGEMENE VORM
De exponentiële functie heeft de volgende algemene vorm:
f: y = ax
De onbekende ‘x’ is de exponent van een getal (a).
Het getal a voldoet aan twee voorwaarden:
• het is strikt positief (groter dan 0)
• het is niet gelijk aan 1 (want 1x = 1 → dit levert een constante functie op)
Exponentiële functies / p.1 van 27 / versie 1
© Edulogos cvba-vso
DIFFERENTIEQUOTIËNT
1. INLEIDING...................................................................................................................................1
2. HET DIFFERENTIEQUOTIËNT...................................................................................................4
3. OEFENINGEN..............................................................................................................................5
4. OPLOSSINGEN...........................................................................................................................7
1. INLEIDING
Van een rechthoekig stuk karton van 20 bij 30 cm knip je aan de vier hoeken gelijke vierkantjes
weg. Je kan de zijkanten nu omhoog plooien. Het resultaat is een rechthoekige doos.
De inhoud van de doos die je verkrijgt, hangt af van de afmetingen die je kiest voor de vierkantjes.
De inhoud van de doos bij de verschillende afmetingen voor de vierkantjes kan je beschrijven met
de volgende functie:
f: y = 4x3 – 100x2 + 600x
(x = zijde weggesneden vierkantjes).
Differentiequotiënt / p.1 van 8 / versie 1
Edulogos cvba-vso
STATISTIEK
1. WAT IS STATISTIEK?..................................................................................................................1
1.1. BASISBEGRIPPEN..............................................................................................................2
1.2. DE STEEKPROEF................................................................................................................3
1.3. KRITISCH OMGAAN MET STATISTIEKEN IN DE MEDIA...................................................4
2. FREQUENTIETABELLEN............................................................................................................5
3. GRAFISCHE VOORSTELLING VAN STATISTISCHE GEGEVENS..........................................10
4. HISTOGRAM TEKEN MET TI84................................................................................................21
5. CENTRUMGETALLEN...............................................................................................................24
5.1. REKENKUNDIG GEMIDDELDE.........................................................................................24
5.2. MEDIAAN...........................................................................................................................27
5.3. MODUS..............................................................................................................................31
6. SPREIDINGSGETALLEN...........................................................................................................31
6.1. KWARTIELEN....................................................................................................................32
6.2. VARIANTIE.........................................................................................................................35
6.3. STANDAARDAFWIJKING..................................................................................................36
7. ALLES IN 1 KEER BEREKENEN...............................................................................................38
1. WAT IS STATISTIEK?
Stel dat je een nieuw soort ontbijtgranen hebt ontwikkeld. Voor je aan de productie en de verkoop
ervan begint, wil je toch wel weten hoe groot de kans is dat je product goed zal verkopen in de
Belgische supermarkten. Je moet dus te weten komen wat de Belgen ‘s ochtends eten, hoeveel geld
ze uitgeven aan ontbijtgranen,...
Natuurlijk is het onbegonnen werk om bij elk gezin te gaan aankloppen om de nodige vragen te
stellen. Daarom maak je een selectie. Je kiest een beperkt aantal gezinnen dat model zal staan voor
alle gezinnen.
De groep waar je informatie over wil = de populatie = alle Belgen
De groep waar je je vragen aan stelt = de steekproef = een beperkte groep Belgen
De statistiek is de wetenschap van het verzamelen, bewerken, interpreteren en voorstellen van
gegevens. Het is een onderdeel van de wiskunde.
Statistici proberen informatie te krijgen over een groep individuen (= een populatie) door een beperkt
aantal van die individuen (= de steekproef) te bestuderen.
De zo verkregen informatie is natuurlijk onvolledig en dus onnauwkeurig. Statistici ontwikkelen allerlei
methodes om de onnauwkeurigheid zo klein mogelijk te maken.
De resultaten van statistisch onderzoek worden gebruikt in de wetenschap, de politiek, de economie,
de psychologie, de sociologie, de media,...
Statistiek / p.1 van 38 / versie 1
DE NORMALE VERDELING
1. KENMERKEN VAN DE NORMALE VERDELING........................................................................1
2. DE GAUSSCURVE......................................................................................................................4
3. INFORMATIE HALEN UIT NORMAAL VERDEELDE GEGEVENS..............................................8
3.1. HOEVEEL % WEEGT, BEVAT,... TUSSEN … ....................................................................9
3.2. HOEVEEL % WEEGT, BEVAT,... MEER OF MINDER DAN …..........................................10
3.3. WAT IS HET GEWICHT, DE LENGTE,... VAN EEN % VAN DE WAARDEN?...................12
4. DE Z-SCORE.............................................................................................................................13
5. DE STANDAARDNORMALE VERDELING................................................................................16
6. DIVERSE OEFENINGEN...........................................................................................................17
7. OPLOSSINGEN OEFENINGEN.................................................................................................20
1. KENMERKEN VAN DE NORMALE VERDELING
De statistiek is geïnteresseerd in de spreiding van meetwaarden. Hoe ver liggen ze van het
gemiddelde? Hoe dicht liggen ze bij elkaar?
Bepaalde soorten gegevens vertonen een heel specifiek spreidingspatroon. Het gaat dan om
eigenschappen van individuen van eenzelfde soort (bv. lengte, gewicht, intelligentie,...),
opeenvolgende prestaties van eenzelfde individu (bv. zwemtijden, gewicht van pakjes gevuld door
eenzelfde machine,...),...
Hoe herken je zo'n spreidingspatroon?
• gemiddelde en mediaan zijn (zo goed als) gelijk
• de dichtheidskromme heeft de vorm van een klok
• er wordt voldaan aan de 68-95-99,7-regel
Werkwijze: dichtheidskromme maken
Neem de frequentietabel met de lengte van de jongens (document Statistiek). Voer de relatieve
frequentie in als L6.
Bereken gemiddelde, mediaan en standaardafwijking → hiervoor gebruik je de absolute frequentie
functie ingeven
Druk op Y =
Zet de cursor bij Y1
Druk "2ND + VARS" en kies optie 1: normalpdf
Er staat nu: Y = normalpdf(
Vul na het haakje het volgende in:
X komma gemiddelde komma standaardafwijking
Sluit het haakje.
Normale verdeling / p.1 van 24 / versie 2