Opgaven 2

Stevin vwo deel 1
Uitwerkingen hoofdstuk 3 – Drie wetten van Newton (20-10-2014)
Pagina 1 van 13
De uitwerkingen met een rood nummer zijn aangepast aan de manier die NiNa prefereert: meer nadruk op
grafieken en gemiddelde snelheid.
Opgaven 3.1 – De traagheidswet van Newton
1
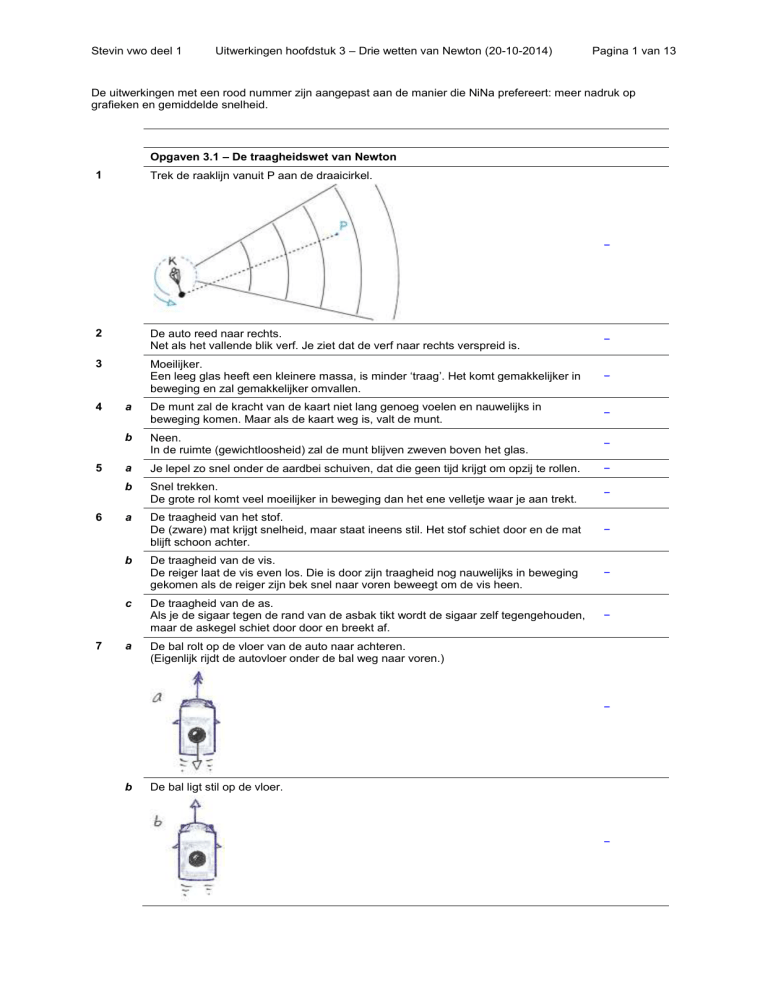
Trek de raaklijn vanuit P aan de draaicirkel.
−
2
De auto reed naar rechts.
Net als het vallende blik verf. Je ziet dat de verf naar rechts verspreid is.
−
3
Moeilijker.
Een leeg glas heeft een kleinere massa, is minder ‘traag’. Het komt gemakkelijker in
beweging en zal gemakkelijker omvallen.
−
a
De munt zal de kracht van de kaart niet lang genoeg voelen en nauwelijks in
beweging komen. Maar als de kaart weg is, valt de munt.
−
b
Neen.
In de ruimte (gewichtloosheid) zal de munt blijven zweven boven het glas.
−
a
Je lepel zo snel onder de aardbei schuiven, dat die geen tijd krijgt om opzij te rollen.
−
b
Snel trekken.
De grote rol komt veel moeilijker in beweging dan het ene velletje waar je aan trekt.
−
a
De traagheid van het stof.
De (zware) mat krijgt snelheid, maar staat ineens stil. Het stof schiet door en de mat
blijft schoon achter.
−
De traagheid van de vis.
De reiger laat de vis even los. Die is door zijn traagheid nog nauwelijks in beweging
gekomen als de reiger zijn bek snel naar voren beweegt om de vis heen.
−
De traagheid van de as.
Als je de sigaar tegen de rand van de asbak tikt wordt de sigaar zelf tegengehouden,
maar de askegel schiet door door en breekt af.
−
4
5
6
b
c
7
a
De bal rolt op de vloer van de auto naar achteren.
(Eigenlijk rijdt de autovloer onder de bal weg naar voren.)
−
b
De bal ligt stil op de vloer.
−
Stevin vwo deel 1
c
Uitwerkingen hoofdstuk 3 – Drie wetten van Newton (20-10-2014)
Pagina 2 van 13
De bal rolt over de vloer met een bocht links naar voren.
(De bal wil gewoon rechtdoor gaan. Eigenlijk rijdt de autovloer onder de bal naar
rechts.)
−
8
9
a
Bij een botsing van achteren.
De hoofdsteun voorkomt dat je hoofd achter blijft bij je bovenlijf, dus achterover klapt
(met kans op een whiplash)
−
b
Bij een botsing van voren.
De autogordel voorkomt dat je doorschiet door de voorruit heen.
−
a
De slinger blijft achter, hangt schuin naar achter (naar links dus).
−
b
De slinger hangt stil omlaag.
−
c
De slinger schiet door, hangt schuin naar voren (naar rechts dus).
−
10
In de figuur links ligt het zwaartepunt van de hamer verder van je vingertop. De
bovenkant van de hamer (meer massa, dus trager) valt daar minder snel opzij. Je
hebt meer tijd om je vinger opnieuw onder het zwaartepunt te brengen.
−
Stevin vwo deel 1
Uitwerkingen hoofdstuk 3 – Drie wetten van Newton (20-10-2014)
Pagina 3 van 13
Opgaven 3.2 – De krachtwet van Newton
De massa van een motor is kleiner dan die van een auto. De motor is minder ‘traag’,
zijn snelheid verandert makkelijker
−
a
F  m  a  0,800  6, 4  5,12  5,1 N
5,1 N
b
F
1,2

 1,5 m/s2
m
0,800
v  a  t  v (0,70)  1,5  0,70  1,05  1,1 m/s
1,1 m/s
a
Naar rechts.
De propeller, waarop een kracht naar links werkt, zet zich af tegen de lucht.
−
b
F  Fpropeller  Fw  Ftrek,1  Ftrek,2  8  1 5  2  10 N , naar links
10 N
c
a
F 10

 2 m/s2 , naar links
m
5
2 m/s2
a
a
v 0,70  0,10

 0,3  0,30 m/s2
t
2,0
0,30 m/s2
b
F  m  a  0,500  0,30  0,15 N
11
12
13
14
F  m  a  a 
0,15 N
c
−
15
a
v  constant  a  0  F  0 , dus de spierkracht is even groot als alle
wrijvingskrachten samen.
b
Met minder spierkracht zal bij de aanvankelijke snelheid de som van de
wrijvingskrachten groter zijn. De snelheid neemt af.
Maar ook Fw ,lucht wordt dan kleiner.
even groot
−
Totdat bij een kleinere snelheid de som van de wrijvingskrachten weer even groot is
geworden als de kleinere spierkracht. Je houdt nu die kleinere snelheid.
F  Fs  Fw  m  a
16
 1 Fw  0,5  0,8  0,4  Fw  1  0,4  0,6 N
17
a
0,6 N
1e manier: met de formule voor de versnelde beweging vanuit rust
x
1 a t2
2
 0,22  t 2 
1a
2
 0,22  a  0,44 m/s2
F  m  a  0,600  0,44  0,264  0,26 N
2e manier: met de gemiddelde snelheid
vgem = x/t = 0,22t2/t = 0,22t
v = 2vgem = 20,22t = 0,44t  a = 0,44t (vergelijk v = 0,44t met v = at)
F = ma = 0,6000,44 = 0,264 = 0,26 N
0,44 m/s2
0,26 N
Uitwerkingen hoofdstuk 3 – Drie wetten van Newton (20-10-2014)
Stevin vwo deel 1
b
F  Fpropeller  Fw
 0,264  Fpropeller  0,12  Fpropeller  0,264  0,12  0,384  0,38 N
Pagina 4 van 13
0,38 N
c
−
18
a
1e manier: met de formule voor de versnelde beweging vanuit rust
x
1 a t2
2
 1,20 
1 a  (1,36)2
2
 0,9248  a  a 
1,20
 1,297..  1,30 m/s2
0,9248
1,30 m/s2
2e manier: met de gemiddelde snelheid
vgem = x/t = 1,20/1,36 = 0,882.. ms−1
vgem = (0 +v)/2  v = 2vgem = 20,882.. = 1,764.. ms−1
a = Δv/Δt = 1,764../1,36 = 1,297.. = 1,30 ms-2
19
b
F  Fpropeller  m  a  0,700  1,297..  0,9083..  0,908 N
0,908 N
a
Met een balans wordt de massa bepaald.
F
2, 48
m  z,Mars 
 0,670..  0,67 kg
gMars
3,7
0,67 kg
b
Krachtmeter: Fz  m  gaarde  0,670..  9,81  6,57  6,6 N
Balans: m = 0,67 kg, zoals overal.
c
Eerst de valversnelling op planeet X bepalen.
1e manier: met de formule voor de vrije val vanuit rust
2  1,80
h  21 g X  t 2  1,80  21 g X  (0,80)2  g X 
 5,62.. m/s2
(0,80)2
F
4,0
m z 
 0,711..  0,71 kg
gX
5,62..
2e manier: met de gemiddelde snelheid
vgem = (0 + v)/2  v = 2vgem
vgem = x/t = 1,80/0,80 = 2,25 ms−1  v = 22,25 = 4,50 m/s
gX = Δv/Δt = 4,50/0,80 = 5,62.. ms−2
m = Fz/gX = 4,0/5,62.. = 0,711.. = 0,71 kg
6,6 N
0,67 kg
0,71 kg
Stevin vwo deel 1
Uitwerkingen hoofdstuk 3 – Drie wetten van Newton (20-10-2014)
Pagina 5 van 13
Opgaven 3.3 – De actie/reactiewet van Newton
20
De terugslag van die kanonnen zou het schip kunnen doen kapseizen.
21
De jongen zweeft! Dus jongen en boot oefenen geen kracht meer op elkaar uit. Dat
gebeurde alleen tijdens de afzet. Toen duwde de jongen de boot naar achter en
tegelijk duwde de boot de jongen even krachtig naar voren.
−
−
22
De hand trekt de haardos van de baron omhoog. Maar tegelijk trekt de haardos de
hand van de baron even krachtig omlaag. Deze twee krachten op de baron heffen
elkaar op.
De netto kracht op de baron is alleen de zwaartekracht. Hij zakt verder weg in het
moeras.
23
De kogel en het geweer zouden een even grote versnelling krijgen.
Immers, Fgeweer kogel  Fkogel geweer  mkogel  akogel  mgeweer  ageweer
−
−
Met mkogel  mgeweer geeft dat akogel  ageweer
24
25
a
Iets weggooien. Of blazen. Door de terugslag kom je in beweging.
−
b
Straalaandrijving van raketmotoren.
−
a
F12   F21   m2  a2  70  1,0  70 N
70 N
b
F21  m1  a1  70  50  a1  a1 
26
27
70
 1, 4 m/s2
50
Zowel op jou als op de kar werkt een kracht van 20 N.
Eerst jouw snelheid:
20
Fop jou  mjij  ajij  20  50  a  a 
 0,4 m/s2
50
v  a  t  v (2,0)  0,4  2,0  0,8  0,80 m/s
Dan de snelheid van de kar:
20
Fop kar  mkar  akar  20  30  a  a 
 0,666.. m/s2
30
v  a  t  v (2,0)  0,666..  2,0  1,33..  1,3 m/s
a
1,4 m/s2
0,80 m/s
1,3 m/s
Eerst de remkracht van de auto berekenen:
Frem  mauto  arem  1000  6,3  6300  6,3  103 N
Hiermee wordt de combinatie afgeremd:
Frem  (mauto  mcaravan )  arem
 6300  (1000  800)  arem  arem 
3,5 m/s2
6300
 3,5 m/s2
1800
b
Beide krachten van dit krachtenpaar zijn natuurlijk even groot.
−
c
Meer stroomlijn betekent minder wrijving (die het remmen zou helpen). Met meer
stroomlijn zal de remweg langer zijn.
−
Uitwerkingen hoofdstuk 3 – Drie wetten van Newton (20-10-2014)
Stevin vwo deel 1
Pagina 6 van 13
Opgaven hoofdstuk 3
28
29
Als de wrijvingskracht even groot geworden is als de motorkracht, is de netto kracht
op het vliegtuig 0 en verandert de snelheid van het vliegtuig niet meer.
Shaw dacht blijkbaar, net als Archimedes vroeger, dat voor het handhaven van
snelheid een kracht nodig is. Wij weten inmiddels dat alleen voor een
snelheidsverandering een netto kracht nodig is.
a
−
1e manier: met de formules voor de versnelde beweging vanuit rust
x
1 a t2
2
 0,30 
1 a  0,122
2
a
2  0,30
 41,6..  42 m/s2
0,144
42 m/s2
2e manier: met de gemiddelde snelheid
vgem = x/t = 0,30/0,12 = 2,5 ms−1
vgem = (0 +v)/2  v = 2vgem = 22,5.. = 5,0 ms−1
a = Δv/Δt = 5,0/0,12 = 41,7.. = 42 ms−2
b
30
31
a
v  a  t  1,7  0,12  0,204  0,20 m/s
0,20 m/s
Op het moment dat je gas terugneemt wordt de motorkracht kleiner dan de
wrijvingskrachten. De brommer vertraagt (negatieve versnelling). De snelheid wordt
kleiner.
Maar dan wordt ook de luchtwrijving kleiner. Totdat bij een bepaalde snelheid de
motorkracht en de wrijvingskrachten weer even groot zijn en je met die kleinere
constante snelheid verder rijdt.
−
Frem  m  arem
 4,3  105  23  103  arem  arem 
4,3  105
23  103
 18,6..  19 m/s2
b
Δv = 0 – 220 km/h = – 61,1.. ms−1 (3,6)
a = Δv/Δt  Δt = Δv/a = (– 61,1..)/ (– 18,6..) = 3,26.. = 3,3 s
c
1e manier: film terugdraaien en de formule voor de versnelde beweging vanuit rust
x
1 a t2
2

1
2
3,3 s
 18,6..  (3,26..)2  99,8..  1,0  102 m
2e manier: via de gemiddelde snelheid
v v
61,1..  0
x  v t  1 2 t 
 3,26..  99,8..  1,0  102 m
2
2
32
19 m/s2
1,0∙102 m
a
−
b
Naar voren. De wrijving tussen de auto en het boek neemt het boek mee naar voren.
−
c
F  m  a  0,500  2,0  1  1,0 N
1,0 N
d
−
33
a
Fpropeller  m  akar
 0,32  0,500  akar  akar 
0,32
 0,64 m/s2
0,500
0,64 m/s2
Uitwerkingen hoofdstuk 3 – Drie wetten van Newton (20-10-2014)
Stevin vwo deel 1
b
Pagina 7 van 13
1e manier: met de formule voor de versnelde beweging vanuit rust
x
1 a t2
2
 1,20 
1 a  (2,55)2
2
a
2  1,20
 0,3690..  0,369 m/s2
6,50..
0,369 m/s2
2e manier: met de gemiddelde snelheid
vgem = x/t = 1,20/2,55 = 0,470.. ms−1
vgem = (0 +v)/2  v = 2vgem = 20,470.. = 0,941.. ms−1
a = Δv/Δt = 0,941../2,55 = 0,3690.. = 0,368 ms−2
c
F  Fpropeller  Fw  m  a
 0,32  Fw  0,500  0,3690..  Fw  0,32  0,1845..  0,135..  0,14 N
34
a
v1  v 2 0  1 106

 0,5  106 m/s
2
2
x  v gem  t
v gem 
 0,05  0,5  106  t  t 
a
35
0,05
0,5  106
 1 10 7 s
0,5∙106 m/s
1∙10−7 s
1∙1013 m/s2
v
1 106

 1 1013 m/s2
t 1 10 7
b
F  m  a  1 1030  1 1013  1 1017 N
1∙10−17 N
a
v constant, dus F  0 ,
dus Fs  Fw ,water  Fw ,lucht  85  5  90 N
90 N
b
F  Fs  Fw ,water  Fw ,lucht  m  a
 Fs  85  5  70  0,60  Fs  70  0,60  85  5  132  1,3  102 N
36
0,14 N
a
In beide gevallen v  constant  F  0
1,3∙102 N
−
b
−
c
Als v naar rechts gericht is, werkt Fw naar links en er geldt
F  Fpropeller  Ftrek  Fw  Fpropeller  0,54  Fw   0
 Fpropeller  Fw  0,54
(1)
Als v naar links gericht is, werkt Fw naar rechts en er geldt
F  Fpropeller  Ftrek  Fw   Fpropeller  0,68  Fw   0
 Fpropeller  Fw  0,68
(2)
Je hebt nu twee vergelijkingen met twee onbekenden:
Fp bereken je uit (2) + (1) =
0,61 N
0,07 N
Fpropeller  Fw   Fpropeller  Fw   2Fpropeller  0,68  0,54  1,22  Fpropeller  0,61 N
Fw bereken je uit uit (2) - (1) =
Fpropeller  Fw   Fpropeller  Fw   2Fw  0,68  0,54  0,14  Fw  0,07 N
37
a
a
v
10  0

 2,27..  2,3 m/s2
t
4,4  0
2,3 m/s2
Stevin vwo deel 1
Uitwerkingen hoofdstuk 3 – Drie wetten van Newton (20-10-2014)
b
F  m  a  132  2,27..  300  3,0  102 N
c
F  Fmotor  Fw
 300  Fmotor  63  Fmotor  300  63  363  3,6  102 N
Pagina 8 van 13
3,0∙102 N
3,6∙102 N
d
Bij constante (top)snelheid is F  0
−
e
F  Fmotor  Fw  0  Fw  Fmotor  363  3,6  102 N
3,6∙102 N
f
Helling bepalen
1,1 m/s2
a
g
10  0,8
 1,05..  1,1m/s2
8,7  0
F  Fmotor  Fw  m  a
 363  Fw  132  1,05..  139,..  Fw  363  139,..  223,..  2,2  102 N
38
a
Dan is F  Fz  FL  0  m  a  a  0 , dus de snelheid verandert niet meer
b
ρlucht = 1,29 kg/m3
2,2∙102 N
-
FL  Fz  21 C    A  v max 2  m  g

2
1  1,42  1,29  57  v
max
2
 70  9,81
 52,2..  vmax 2  686,..  vmax 
3,6 m/s
686,..
 3,62..  3,6 m/s
52,2..
c
−
Bij een vrije val wordt de snelheid van 30 m/s bereikt na ongeveer 3 s en een val van
ongeveer 45 m. Door de wrijving wordt die snelheid wat later bereikt. De val zal wat
dieper zijn, ruim 50 m.
Stevin vwo deel 1
d
39
a
b
Uitwerkingen hoofdstuk 3 – Drie wetten van Newton (20-10-2014)
v1  v 2 45  5

 25 m/s .
2
2
De duur van de vertraging bereken je uit
30
h  v gem  t  30  25  t  t 
 1,2 s
25
v 5  45
33,3..
Dan a 

 33,3..  a 
 3,39..  3,4  g
t
1,2
9,81
Pagina 9 van 13
Tijdens de vertraging is v gem 
- 3,4∙g
Fz  mdruppel  g


mdruppel  water  Vbol 

  Fz 
3
4
Vbol  3  r

3
3 
water  1 10 kg/m 
4 r3
3
 1 103  g
−
Bij constante eindsnelheid is F  0  FL  Fz
1
2
 0,6  1,3   r 2  v 2 
 v2 
4 r3
3
4  r 3  1 103  g
3
1  0,6  1,3   r 2
2

 1 103  g
4  103  9,81
r3
3
 2
1  0,6  1,3
r
2
 33,5..  103  r
−
 v  33,5..  103  r  183,..  r
Dus v evenredig met √r : hoe groter de druppel, des te groter de eindsnelheid.
c
v  183,..  r  183,..  2,0  10 3  8,19..  8,2 m/s
d
Met behulp van de Modelomgeving in Coach zijn de volgende grafieken gemaakt :
8,2 m/s
−
De eindsnelheid wordt bereikt na ongeveer 2,5 s. De druppel heeft dan ongeveer
15 m afgelegd.
40
a
Schrap zetten betekent: met de hakken in de klei het weiland naar voren duwen
(actie), tegelijk duwt dan het weiland de ploeg naar achter (reactie). Met precies die
kracht wordt via het touw aan de tegenstander getrokken. Wie dat het beste kan,
trekt de andere ploeg mee.
−
Stevin vwo deel 1
b
Uitwerkingen hoofdstuk 3 – Drie wetten van Newton (20-10-2014)
Pagina 10 van 13
Dit zijn de krachten op de deelnemers. De rechter ploeg verliest.
−
Dit zijn de krachten op het touw.
41
42
1. Ja.
Zolang de hond de worst niet te pakken heeft trekt hij de kar naar voren.
−
2. Neen.
Wel wordt door het blazen een kracht naar voren uitgeoefend op het zeil, en dus op
de boot. Maar de blazende roerganger, en dus de boot, ondervindt tegelijk een
even grote kracht naar achter. De netto kracht op de boot is nul.
−
3. Neen.
Wel trekt de magneet de trein naar voren. Maar tegelijkertijd trekt de trein de
magneet even hard naar achter. Die kracht werkt via de hengel en de ‘machinist’
weer op de trein. De netto kracht op de trein is nul.
−
4. Ja.
Door de aandrijving met de föhn duwt de schroef het water naar achter en het
water de schroef, en dus de boot, naar voren.
−
a
Het is een krachtenpaar: Faardesteen  Fsteen aarde
−
b
De afzetkracht van één chinees volgt uit:
Fafzet  Fz  m  a  Fafzet  m  g  m  (1,5  g )  Fafzet  m  g  m  (1,5  g )  m  (2,5  g )
Stel dat de gemiddelde massa van een chinees (baby’s, kinderen en volwassenen)
40 kg is. Eén miljard chinezen samen duwen de aarde weg met een kracht


Fchinezen aarde  1 109  40   2,5  10   1 1012 N
10−14 m/s2
De versnelling van de aarde (maarde  6,0  1024 kg; Binas tabel 31) volgt uit:
Fchinezen aarde  maarde  aaarde
 1 1012  6,0  1024  aaarde  aaarde 
43
1 1012
24
6,0  10
 2  1013 m/s2
a
0,20 N
F  0  Fspan  Fz
 Fspan  Fz  m  g  20  103  9,81  0,196..  0,20 N
b
F  0  (M  m )  a  a  0 m/s2
0 m/s2
Uitwerkingen hoofdstuk 3 – Drie wetten van Newton (20-10-2014)
Stevin vwo deel 1
c
d
M en m krijgen na het loslaten dezelfde versnelling a, er geldt:
ΣFm = Fz,m - Fspan = m∙a (en voor M geldt: ΣFM = Fspan = M∙a )
Fz is niet veranderd, dus uit ΣFm ≠ 0 volgt dat Fspan kleiner is geworden.
Pagina 11 van 13
−
F  Fz,m  (M  m )  a
m  g  (M  m )  a
 m  9,81  0,200  0,15  m  0,15
3,1 g
 m   9,81  0,15   0,200  0,15
m
44
a
0,03
 3,10..  103  3,1 10 3 kg
9,66
1e manier: met de formule voor de versnelde beweging vanuit rust
x
1 a t2
2
 1,60 
1 a  (1,67)2
2
a
2  1,60
2
(1,67)
 1,147..  1,15 m/s2 Klopt
2e manier: met de gemiddelde snelheid
vgem = x/t = 1,60/1,67 = 0,958.. m−1
vgem = (0 +v)/2  v = 2vgem = 20,958.. = 1,916.. m−1
a = Δv/Δt = 1,916../1,67 = 1,147.. = 1,15 ms-2 Klopt
b
c
x
20  103

 1,92..  1,9 m/s
t 10,4  103
Opmerking: bij een eenparig versnelde beweging is dit ook de echte snelheid
halverwege de passeertijd.
−
v gem 
1,9 m/s
v  1,92..  0  1,92.. s
t  1,67 
10, 4  10
2
3

v
1,92..


 1,147..  1,15 m/s2
a
t 1,675..
 1,675.. s 

−
(!) Zie opmerking bij b
45
d
F  (mslee  mgewichtje )  a  (0,200  0,030)  1,147..  0,2640..  0,264 N
0,264 N
e
0,2640..
 8,80..  8,8 m/s2
0,030
De planeet zou Venus kunnen zijn. Zie Binas tabel 31.
8,8 m/s2
a
F  mgewichtje  g  0,2640..  0,030  g  g 
1e manier: met de formule voor de versnelde beweging vanuit rust
h
1 a t2
2
 1,50 
1 a  (2,90)2
2
a
2  1,50
(2,90)2
 0,3567..  0,357 m/s2
2e manier: met de gemiddelde snelheid
vgem = x/t = 1,50/2,90 = 0,517.. ms−1
vgem = (0 +v)/2  v = 2vgem = 20,517.. = 1,03.. ms−1
a = Δv/Δt = 1,03../2,90 = 0,3567.. = 0,357 ms−2
0,357 m/s2
b
m  250  250  28  528 g
528 g
c
F   m  a  0,528  0,3567..  0,1883..  0,188 N
0,188 N
d
Van de massa van het extra gewichtje rechts is 8 g nodig om de wrijving van de
katrol te overwinnen. Voor het versnellen blijft dan nog 20 g over.
−
F  m  g  20  103  g
e
g
F 0,1883..

 9,41..  9,4 m/s2
m
0,020
9,4 m/s2
Stevin vwo deel 1
Uitwerkingen hoofdstuk 3 – Drie wetten van Newton (20-10-2014)
Pagina 12 van 13
Toets
1
Een steen op de maan
a
Fspier  Fz,maan  m  gmaan  0,76  1,63  1,23..  1,2 N
b
F  Fspier  Fz  2,50  1,23..  1,26.. N
F  m  a  1,26..  0,76  a  a 
c
d
2
1,26..
 1,65..  1,7 m/s2
0,76
1,2 N
1,7 m/s2
De astronaut gooit de steen schuin omhoog, zodat die met een boog in de jeep zal
vallen. Maar als de voorwaartse snelheid even groot is als op aarde zal de steen over
de jeep heen vliegen, want door de geringere zwaartekracht op de maan daalt de
steen daar niet zo snel als op aarde.
−
Als hij met grote kracht gooit, zou hij door de terugslag achterover kunnen vallen. Die
kans is door het kleinere gewicht op de maan groter dan op aarde: de resultante van
reactiekracht en zwaartekracht is op de maan meer naar achteren gericht dan op
aarde.
−
De maanjeep
a1
v  54 km/h  3,6   15 m/s
a
a2
v
15

 2,58..  2,6 m/s2
t
5,8
F  Fmotor  Fw  m  a
 Fmotor  150  480  2,58..  Fmotor  480  2,58..  150  1391,..  1, 4  103 N
2,6 m/s2
1,4∙103 N
b
−
c
Horizontaal gerichte krachten op de steen:
F  Fspan  Fw  m  a
52 N
 Fspan  50  0,76  2,5  Fspan  0,76  2,5  50  51,9  52 N
3
Een blaaspijp
a1
a2
b
vB 
x 8,5  102

 19,7..  20 m/s
t
4,3  103
v gem,AB 
0  v B 0  19,7..

 9,88..  9,9 m/s
2
2
20 m/s
9,9 m/s
Bereken eerst hoe lang de viltstift in de blaaspijp zit.
l AB  v AB  t AB
 t AB 
a
l AB
2,00

 0,202.. s
v AB 9,88..
v AB
19,7..

 97,6..  98 m/s2
t AB
0,202..
98 m/s2
Uitwerkingen hoofdstuk 3 – Drie wetten van Newton (20-10-2014)
Stevin vwo deel 1
c
F  Fblaas  m  a  0,020  97,6..  1,95..  2,0 N
d
1e
Pagina 13 van 13
2,0 N
manier: met de oppervlakte onder de v(t)-grafiek
De v(t)-grafiek ziet er − als de viltstift een constante versnelling heeft − zo uit:
Het oppervlak onder de v(t)-grafiek is de lengte van de blaaspijp = 2,00 m.
Dit oppervlak is in vier gelijke driehoeken te verdelen, want tAP = ½tAB.
Het oppervlak van driehoek no. 1 = 2,00/4 = 50 cm, dus P zit 50 cm van A af.
0,50 m
2e manier: met de gemiddelde snelheid
De gemiddelde snelheid van de viltstift tussen A en P is de helft van de gemiddelde
snelheid van de viltstift tussen A en B: vgem,AP = ½vgem,AB = ½9,88.. = 4,94.. ms−1.
tAP = ½0,202..= 0,101.. s
XAP = vgem,APtAP = 4,94..0,101 = 0,50 m
3e manier: met de formule voor de versnelde beweging vanuit rust
t AP  tPB 
1 t
AB
2
 xAP 
 t AP 2  21  9,88..  0,101..2  0,5  0,50 m
1 a
2

1  0,202.. 
2
0,101.. s
Of zo:
t AP  tPB 
1
2
t AB
 x AP 
1 a
2
 t AP 2  21 a   21 t AB 
 x AP 
1
4
 2,00  0,5  0,50 m
2

1 a 1
2
4
 t AB 2  41 

1a
2
 t AB 2

1
4
 xAB