Newton - 9 Elektromotor

Newton 5 vwo
Natuurkunde
voor de
2e
fase
Hoofdstuk 9  Elektromotor
Hoofdstuk 10  Dynamo en transformator
les dag



klassikaal/docent
groepje/huiswerk
1
Oriëntatie (1/2 les)
bundel blz. 3 en 4
2
Magnetisch veld (1/2 les?)
bundel blz. 5 t/m 8
3
Lorentzkracht
bundel blz. 9 t/m 12
4
Elektromotor
bundel blz. 13 t/m 15
5
Stroomdraad en Lorentzkracht
bundel blz. 16 t/m 20
6
Afronden hoofdstuk 9
7
Voortgangstoets
8
Inductiespanning
bundel blz. 21 t/m 24
9
Dynamo
bundel blz. 25 t/m 27
10
Vallende magneet
bundel blz. 28 t/m 30
11
Effectieve spanning
bundel blz. 31 t/m 35
12
Transformator
bundel blz. 36 t/m 38
13
Toepassingen transformatoren
bundel blz. 40 t/m 46
14
Afronden hoofdstuk 10
15
Voortgangstoets
16
Toets in de 1e toetsweek: hoofdstuk 9 en 10
Hoofdstukvragen:
Hoofdstuk 9 en 10 gaan over elektromagnetisme, over de werking van
elektromotoren, dynamo’s, transformatoren en condensatoren.
 Hoe kun je met elektriciteit magnetisme maken?
 Hoe kunnen elektriciteit en magnetisme voor een kracht zorgen?
 Hoe werkt een elektromotor?
 Hoe zorgt een dynamo voor elektrische energie?
 Hoe kun je met een transformator een wisselspanning veranderen?
 Hoe maak je van wisselspanning gelijkspanning?
 Waarom wordt bij het transport van energie hoogspanning gebruikt?
Materiaal
Bij deze onderzoeken hebben we verschillende elektromotoren, dynamo’s en
adapters nodig. Waarschijnlijk heb je thuis nog wel de nodige elektrisch
apparatuur liggen die niet meer gebruikt zal worden. Daarbij zit vaak een
adapter (los of ingebouwd), en als er iets kan bewegen aan het apparaat zit
er ook een elektromotor is.
Vraag aan je ouders of het apparaat gesloopt mag worden, en neem de
elektromotor of adapter mee naar school. Wellicht hebben jullie thuis ook
nog een (oude) fietsdynamo die niet meer gebruikt wordt.
Project Probleemgerichte didactiek
8e editie, juni 2010
St. Bonifatiuscollege, burg. F. Andreaelaan 7, 3582 KA Utrecht
tel 030-2512315, website: www.boni.nl
Uitvoerders:
Ad Migchielsen
Carolien Kootwijk
Cor Buijs
Kees Hooyman
Otto Kool
Technische ondersteuning:
Marti van IJzendoorn
Newton - hoofdstuk 9 & 10
Elektromotor, dynamo en transformator
Inleiding
Elektromagnetisme
De hoofdstukken 9 en 10 gaan over het verschijnsel elektromagnetisme en
over een groot aantal toepassingen daarvan: de elektromotor, de dynamo en
de transformator. Die toepassingen komen we overal tegen, in vrijwel elk
elektrisch of technisch apparaat zit wel een van deze drie elementen.
Het doel bij dit onderwerp is om enerzijds te ontdekken welke verschijnselen
er achter deze apparaten zit en anderzijds om te zien hoe die apparaten
werken.
In deze inleiding gaan we na wat we al weten van het onderwerp
elektromagnetisme. Welke apparaten ken je al? Weet je hoe die apparaten
werken? Wat weet je van het verschijnsel elektromagnetisme.
Oriëntatie
Elektrische apparaten
Op de onderstaande afbeeldingen zie je enkele apparaten die gebruik maken
van elektromagnetisme: microfoon, luidspreker, elektromotor, dynamo,
aardlekschakelaar, transformator en veiligheidstrafo.
 Welke apparaten herken je?
 Wat weet je al van de werking van die apparaten?
 Wat weet je al van elektromagnetisme?
3
Oriëntatie
De ‘truc’ van een hybride auto
Een hybride auto wordt aangedreven door twee verschillende
aandrijftechnieken: een normale verbrandingsmotor en een elektromotor die
tegelijk dienst doet als dynamo. De verbrandingsmotor van de hybride auto
is kleiner, zuinig en gebruikt geavanceerde technieken om de uitstoot te
beperken. Een hybride auto is ook voorzien van grote accu’s
De eerste hybride auto in serieproductie: de Toyota Prius.
De Honda Civic heeft een
supercompacte
elektromotor/dynamo die maar
6,5 cm dik is. De motor wordt
tussen de benzinemotor en
conventionele transmissie te
zetten. Hij dient ook als starter
en om het 12 V boordnet te
voeden.
De elektrische motor van een hybride auto is voorzien van veel elektronica
die ervoor zorgt dat de elektromotor zowel als een motor en een dynamo kan
fungeren. Zo haalt de hybride auto energie uit de accu's om te accelereren,
waar de elektromotor goed bruikbaar voor is dankzij zijn hoge koppel bij
stilstand. Maar wanneer de hybride auto vertraagt, werkt de elektromotor als
dynamo die energie opslaat in de accu's. Ook als de accu’s gedeeltelijk leeg
zijn werkt de elektromotor als dynamo waardoor de accu’s opgeladen
worden.
Verder wordt de elektromotor gebruikt in de file, in de stad, bij het
inparkeren en bij het achteruitrijden. Bij hoge snelheid op de snelweg rijdt
de motor enkel op zijn verbrandingsmotor.
 Een hybride auto is een stuk zuiniger dan een gewone auto. Beschrijf in je
eigen woorden hoe dat komt.
 De elektromotor van een hybride auto kan ook gebruikt worden als
dynamo. Hoe kan dat? Zou dat voor elke elektromotor of dynamo gelden?
De hybride auto heeft een sterke elektromotor. Voor deze motor is een aparte
accu nodig die een spanning van 200 volt levert. Een accu in een normale
auto levert een spanning van 12 volt.
 Waarom denk je dat een normale accu niet geschikt is voor zo’n sterke
elektromotor?
 Waardoor is het niet eenvoudig om een accuspanning van 12 volt om te
zetten naar een spanning van 200 volt, bijvoorbeeld met een
transformator?
4
Newton - 9 Elektromotor
§2 Magnetisch veld
Nieuwe begrippen
Elementaire magneten
Magnetische influentie
Magnetische veldlijnen
Magnetische inductie
Rechterhandregel spoel
Herhaling
Wat gaan we doen?
Om het verschijnsel elektromagnetisme beter te begrijpen is het van belang
om eerst de eigenschappen van een permanente magneet en van een
elektromagneet te beschrijven en verklaren.
 Hoe komt het dat een permanente magneet wel ijzer maar geen koper
aantrekt?
 Welke betekenis hebben de magnetische veldlijnen?
 Hoe werkt een kompas?
IJzer en magnetisme (kernstof, Newton blz. 10 t/m 15)
Een voorwerp van ijzer is niet vanzelf magnetisch. Twee ijzeren voorwerpen
oefenen geen kracht op elkaar uit. Dat geldt ook voor andere metalen zoals
koper, zink, goud. Alleen ijzer, nikkel en kobalt hebben de eigenschap dat zij
aangetrokken worden door een magneet.
Op de foto zie je een magneet en een stuk ijzer. De magneet heeft aan de
bovenkant een noordpool. Aan het ijzervijlsel is te zien dat het stuk ijzer ook
magnetisch is geworden.
 Welke pool zit er aan de onderkant van het stuk ijzer? In welke richting
lopen de veldlijnen?
 Hoe kan het dat een ijzeren voorwerp zelf magnetisch wordt als het in de
buurt van een magneet komt?
Bij een kompasnaald geldt: De kompasnaald gaat in de richting van de
veldlijnen van het aardmagnetisch veld staan. De magnetische noordpool
van de kompasnaald wijst dan (ongeveer) naar het geografische noorden.
 Heeft het geografisch noorden van de aarde een magnetische zuidpool of
een magnetische noordpool? Leg uit.
Magnetische veldlijnen
Rond een magneet is sprake van een magnetisch veld. Het magnetisch
veld kan zichtbaar gemaakt worden met behulp van ijzervijlsel. De
veldlijnen geven de richting van het magneetveld aan: veldlijnen lopen
buiten de magneet van Noord naar Zuid.
Daarnaast geven de veldlijnen een beeld van de sterkte van het
magneetveld (de magnetsiche inductie) . Waar de veldlijnen dicht bij
elkaar lopen is de magnetische werking groot.
5
Ontdekken
Elektromagnetisme en aardmagnetisme
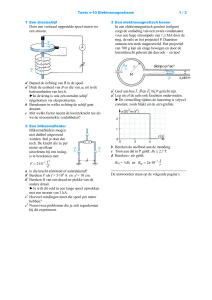
In de figuur hiernaast zie je het veldlijnenpatroon van een permanente
magneet en het veldlijnenpatroon van een stroomspoel. Bij een permanente
magneet geldt: de veldlijnen lopen van de noordpool naar de zuidpool. Bij
een stroomspoel klopt die regel niet meer helemaal, kijk maar naar de
veldlijnen binnen de spoel.
 Verbeter de uitspraak “Magnetische veldlijnen lopen van de noordpool
naar de zuidpool”.
In de tweede figuur zie je een bovenaanzicht van een stroomspoel en een
kompasnaald. In eerste instantie loopt er geen stroom door de spoel. De
kompasnaald bevindt zich in het midden van de spoel en wordt gericht door
het aardmagnetisch veld. De kompasnaald wijst dus naar het Noorden.
De stroom door de stroomspoel wordt langzaam opgevoerd.
 In welke richting zal de kompasnaald draaien?
N
De sterkte van het magnetische veld wordt ook wel de magnetische inductie
genoemd. Voor de sterkte van het magneetveld binnen een spoel geldt:
B  0 
N I
l
Hierin is B de sterkte van het magneetveld (in tesla), μ0 is een constante (zie
BINAS, tabel 7: 1,25664∙10-6), N is het aantal windingen van de spoel, I is de
stroomsterkte (in A), en l de lengte van de spoel (in m).
 De stroom wordt opgevoerd totdat de kompasnaald 45° gedraaid is. Leg uit
dat de sterkte van het magneetveld van de spoel op dat moment gelijk is
aan de sterkte van het aardmagnetisch veld.
In Europa is de sterkte van het aardmagnetisch veld ongeveer 4,8∙10-5 T.
 Bereken welke stroomsterkte nodig is door een spoel met N = 100 en l =
0,06 m om een magneetveld met gelijke sterkte te maken.
Applet
Bekijk het magnetisch veld
met de applets van PhET.
Elektromagneet
Als er door een spoel een elektrische stroom loopt dan ontstaat er een
magneetveld, zoals in de figuur te zien is. Voor de richting van het
magneetveld geldt de rechterhandregel: als de vingers in de richting van
de elektrische stroom wijzen, dan geeft de duim de noordpool van de
elektromagneet aan, en het elektrische veld is dus ook in de richting van
de duim. De veldlijnen in de tekening geven ook de richting van het
magneetveld aan.
6
Theorie
Lees de theorie op blz. 10 t/m 18 in Newton. Om de kern van de theorie goed
samen te vatten maken we gebruik van begrippen- en formuleschema’s.
Elementaire magneten
Magnetische influentie
Magnetische veldlijnen,
veldlijnendichtheid
Magnetische inductie
Rechterhandregel
stroomspoel
Formulelijst
Noteer bij de onderstaande formules: - Wat betekent elk symbool? - Welke
eenheid hoort bij elk symbool? - Wanneer kun je de formule toepassen?
B  0 
N I
l
1
Opgaven
In de figuur zie je een aantal verschillende magneten, combinaties van twee
of meer magneten en combinaties van een magneet en een stuk weekijzer.
Teken in elk van deze situaties het veldlijnenpatroon. (Controleer zo nodig je
antwoorden door het veldlijnenpatroon zichtbaar te maken met een
veldlijnenbord of ijzervijlsel)
7
2
Een permanente magneet wordt gemaakt door een stuk staal enige tijd
binnen een stroomspoel te plaatsen, zoals weergegeven in figuur 10.
Leg uit welk uiteinde van de nieuwe permanente magneet de noordpool en
welk uiteinde de zuidpool is.
3
Leg uit of de twee stroomspoelen van figuur 11 een aantrekkende of een
afstotende kracht op elkaar uitoefenen.
4
In een spoel loopt een stroom met een stroomsterkte van 1,4 A. Deze stroom
veroorzaakt binnen de spoel een magnetisch veld met een sterkte van 24 mT.
Bereken het aantal windingen per meter spoellengte.
5
Noem minstens drie toepassingen van een elektromagneet. Leg bij elk van
die toepassingen uit waarom een elektromagneet wordt gebruikt en niet een
permanente magneet.
8
Newton - 9 Elektromotor
§3 Lorentzkracht
Nieuwe begrippen
Luidspreker
Lorentzkracht
Draaispoelmeter
Ontdekken
Wat gaan we doen?
In veel apparaten die gebruik maken van elektromagnetisme zit zowel een
spoel als een magneet. Het apparaat bevat dus zowel een permanente
magneet als een elektromagneet. Omdat beide voorwerpen magnetisch zijn
kunnen ze een kracht op elkaar uitoefenen (de Lorentzkracht).
 Op welke manier oefenen een permanente magneet en een spoel een
kracht op elkaar uit? Hoe bepaal je de grootte en de richting?
Spoel en magneet in een luidspreker (context)
In de onderstaande afbeeldingen wordt de werking van een luidspreker
verklaard. Een spoel is vastgemaakt aan een beweegbaar membraan, de
conus. De spoel bevindt zich in of vlakbij een permanente magneet.
 Beschrijf in je eigen woorden waarom een luidspreker alleen werkt met
wisselspanning.
 Hoe zijn de toonhoogte en de geluidssterkte te regelen?
 Leg uit hoe een stroomspoel een kracht kan uitoefenen op een magneet.
 Oefent de magneet nu ook een kracht uit op de spoel? Leg uit.
Als de permanente magneet een kracht uitoefent op de spoel dan kan dat
eigenlijk alleen als het magnetisch veld een kracht uitoefent op de elektrische
stroom. Beter gezegd: er werkt een kracht (de Lorentzkracht) op de deeltjes
die bewegen in de spoel, de elektronen.
 Betekent dit dat er op elke stroomdraad die zich in een magnetisch veld
bevindt een kracht werkt?
De Lorentzkracht is vernoemd
naar de Nederlander Hendrik
Antoon Lorentz, die al op zijn
24e hoogleraar in Leiden werd.
Op de foto staat hij naast
Albert Einstein.
 Hoe zou je kunnen onderzoeken of de Lorentzkracht ook werkt op een rechte
stroomdraad?
9
Demonstratie
Lorentzkracht (kernstof, Newton blz. 24 en 25)
Een elektromotor, een luidspreker en een draaispoelmotor werken allemaal
volgens hetzelfde principe: een elektrische spoel en een magneet oefenen een
kracht op elkaar uit. Dat betekent dat er op een elektrische stroom in een
magnetisch veld een kracht werkt. Die kracht noemen we de Lorentzkracht.
De Lorentzkracht heeft, net als de elektrische stroom en het magneetveld een
richting. Voor die richting geldt de rechterhandregel.
 Controleer of de richting van de Lorentzkracht in de demonstratie overeen
komt met de richting uit de tekeningen.
 Bepaal voor elk van de drie onderstaande situaties de richting van de
Lorentzkracht FL op de stroomdraad.
Toepassing
Draaispoelmeter (context, Newton blz. 32)
Een stroommeter bestaat uit een draaibare stroomspoel in het magnetisch
veld van twee permanente magneten. Zo'n stroommeter wordt daarom een
draaispoelmeter genoemd. In de tekening zij slechts enkele windingen van
de spoel weergegeven. De spoel is bevestigd op een draaias, met aan het
uiteinde een spiraalveer. Als er geen stroom door de spoel loopt dan staat de
wijzer verticaal, zoals getekend in de figuur.
 Op welk deel van de spoel werkt de Lorentzkracht die de spoel doet
draaien?
 Leg uit waardoor de wijzer verder gedraaid wordt naarmate de stroom
groter wordt.
 Teken de richting van de stroom in de spoel als de wijzer naar rechts draait.
 Van welke factoren zal de grootte van de Lorentzkracht afhangen?
10
Theorie
Lees de theorie op blz. 24 t/m 27 in Newton. Om de kern van de theorie goed
samen te vatten maken we gebruik van begrippen- en formuleschema’s.
Lorentzkracht
Rechterhandregel bij de
Lorentzkracht
Luidspreker
Draaispoelmeter
Formulelijst
Noteer bij de onderstaande formules: - Wat betekent elk symbool? - Welke
eenheid hoort bij elk symbool? - Wanneer kun je de formule toepassen?
FL  B  I  l
Opgaven
6
Bepaal in de situatie van figuur 26 waar de Noord- en de Zuidpool van de
magneet zitten.
7
Bepaal in de situatie van figuur 27 de richting van de stroom I in de
stroomdraad.
8
Een stroomdraad AB hangt tussen de polen van een magneet, zoals
weergegeven in figuur 30. Bij deze magneet beperkt het magnetisch veld zich
ruwweg tot de ruimte tussen de twee magneetpolen. In deze ruimte is het
magnetisch veld vrijwel homogeen. Noem drie factoren die de grootte van de
Lorentzkracht op de stroomdraad beïnvloeden en drie factoren die dat niet
doen.
11
9
Twee geleidende staven AB en CD liggen op een afstand van 24 cm van
elkaar. Deze staven bevinden zich in een verticaal homogeen magnetisch
veld, zoals weergegeven in figuur 31. De magnetische inductie B in dit veld is
0,92 T. Dwars op de twee staven ligt een geleidende staaf EF met een lengte
van 30 cm. De staafuiteinden B en C worden aangesloten op een
gelijkspanningsbron, zodat in de staaf EF een stroom van 0,58 A loopt.
Daardoor rolt deze staaf naar rechts.
a Bepaal de richting van de stroom in de staaf EF.
b Bereken de grootte van de Lorentzkracht op de staaf EF tijdens het rollen.
10
Luidspreker
In een luidspreker bevindt zich een spoel in het veld van een ringmagneet,
zoals schematisch weergegeven in figuur 43. De beide doorsneden (in
zijaanzicht en in vooraanzicht) in deze figuur zijn op ware grootte. De
koperdraad waarvan de spoel gemaakt is, heeft een lengte van 40 m. Op de
plaats van de spoel is de magnetische inductie 190 mT. De conus met spoel
van de luidspreker is op te vatten als een massa-veersysteem met een
veerconstante van 1,6∙10³ N/m.
a Laat met behulp van figuur 43 zien dat de spoel 1,1∙10³ windingen heeft.
Meet daarvoor de diameter van de spoel.
b Op een bepaald moment loopt de stroom door de windingen van de spoel
zoals weergegeven in figuur 43. Hierdoor ondervindt elke winding van de
spoel een kracht. Bepaal de richting van die kracht in een aantal punten
van de winding.
c Op een bepaald moment zorgt de versterker voor een stroomsterkte van
0,23 A in de spoel. Bereken de kracht op de spoel.
d Bereken de uitwijking van de conus onder invloed van deze kracht op de
spoel.
12
Newton - 9 Elektromotor
§3 Lorentzkracht
Nieuwe begrippen
Gelijkstroommotor
Wisselstroommotor
Rotor, stator en
commutator
Ontdekken
Wat gaan we doen?
De meest gebruikte toepassing van de Lorentzkracht is waarschijnlijk de
elektromotor. In elk elektrisch apparaat waarin iets bewogen wordt zit een
elektromotor. In een moderne auto vind je bijvoorbeeld naast de startmotor
ook elektromotoren voor de ramen, de ruitenwissers, de spiegels, de sloten
op de deuren, de airco enzo.
 Hoe werkt een elektromotor?
Elektromotor (kernstof + context, Newton blz. 27 t/m 31)
Een elektromotor bestaat meestal uit een magneet en één of meerdere
spoelen. De Lorentzkracht zorgt ervoor dat de spoel (of de magneet) gaat
draaien. Hoe zorg je ervoor dat de spoel in beweging blijft?
In de twee onderstaande figuren zie je een spoel van één rechthoekige
winding in een magneetveld.
Bij een moderne elektromotor wordt een groot
aantal spoelen gebruikt
waardoor beurtelings een
stroom loopt.
 Geef in de linkerfiguur de richting van de stroom in de winding aan.
Applet
Bekijk de werking van een
gelijkstroommotor met de
applets van W. Fendt.
 Geef bij elke zijkant van de winding de richting van de Lorentzkracht aan.
 Bij de rechterfiguur werkt er op slechts twee zijkanten van de winding een
Lorentzkracht. Welke twee zijkanten zijn dat? Leg uit.
 Beschrijf in je eigen woorden hoe door het sleepcontact en de koolborstels
wordt gezorgd dat de spoel in beweging blijft.
Lees de tekst op blz. 29-31 over de gelijkstroom- en wisselstroommotor.
 Beschrijf het verschil tussen een gelijkstroom- en een wisselstroommotor.
13
Theorie
Lees de theorie op blz. 27 t/m 31 in Newton. Om de kern van de theorie goed
samen te vatten maken we gebruik van begrippen- en formuleschema’s.
Rotor, stator, commutator
Gelijkstroom- of
wisselstroommotor
11
Opgaven
Een grote spoel met een lengte van 15 cm heeft 3000 windingen. Door deze
spoel loopt een stroom IS van 2,2 A.
a Bereken de sterkte van het magneetveld van de grote spoel.
Binnen de spoel staat een (kleinere) spoel op een draaias, zoals weergegeven
in figuur 34. Deze spoel bestaat uit één vierkante winding met een zijde van
1,5 cm. In deze winding loopt een stroom IW van 50 mA.
b Bepaal de richting en bereken de grootte van de Lorentzkracht F L op elk
van de vier zijden van de winding.
c Leg uit waardoor de kleinere spoel niet in beweging komt.
12
Door de rechthoekige spoel van figuur 35 loopt een gelijkstroom I van 128
mA. De spoel heeft 50 windingen. De spoel bevindt zich in een homogeen
magnetisch veld met een magnetische inductie B van 0,48 T. De spoel is
bevestigd op een verticale draaias.
a In welke richting zal de spoel onder invloed van de Lorentzkrachten op de
vier zijden van de spoel vanuit de getekende beginstand gaan bewegen?
b Bereken de Lorentzkracht op de zijde AB van de spoel in de beginstand.
c In welke stand komt de spoel even later tot rust?
d Bereken de grootte van de Lorentzkracht als de spoel vanuit de
beginstand gedraaid is over een hoek van respectievelijk 90°.
14
13
Faraday-pomp
In sommige kerncentrales wordt vloeibaar natrium gebruikt als koelvloeistof.
Deze vloeistof wordt rondgepompt met een zogenaamde Faraday-pomp. De
werking van deze in figuur 44 weergegeven pomp berust op de
Lorentzkracht.
In de buis zit vloeibaar natrium. Via de twee koperen elektroden kan een
elektrische stroom door het vloeibare natrium in de buis lopen. De
richtingen van het magnetisch veld en de elektrische stroom staan loodrecht
op elkaar.
a Leg uit hoe deze pomp zorgt voor een stroming van het vloeibaar natrium
in de buis.
b Beredeneer in welke richting het natrium door de buis stroomt.
Via de twee koperen elektroden loopt een elektrische stroom van 90 A door
het vloeibare natrium. De binnendoorsnede van de buis tussen de
magneetpolen is 5,0 mm hoog en 22 mm breed. De twee magneetpolen
veroorzaken een homogeen magnetisch veld met een sterkte van 0,78 T.
c Bereken de grootte van de Lorentzkracht in de pompbuis.
Verdieping (NT)
Spoel in magneetveld
Een spoel is opgehangen aan een krachtmeter, gedeeltelijk tussen de polen
van een magneet. De vorm van de spoel is rechthoekig, 10,0 cm hoog 8,0 cm
breed. De spoel heeft 200 windingen.
Grootheden & eenheden
De formule voor de
Lorentzkracht biedt ook
een goede mogelijkheid
om de sterkte van het
magnetisch veld (in Tesla)
te meten.
FL  B  I  l
Een magnetisch veld met
een sterkte van 1 tesla
oefent een kracht van 1
newton uit op 1 meter
draad waardoor een
stroom van 1 ampère loopt.
1T  1
N
A m
Als er een stroom door de spoel loopt dan wordt de spoel naar beneden
getrokken.
 Op welke delen van de spoel werkt dan de Lorentzkracht? Geef de richting
aan in de tekening.
Wanneer de stroom opgevoerd wordt blijkt de aanwijzing van de
krachtmeter te veranderen. De metingen staan in de grafiek.
 Verklaar de vorm van de grafiek. (dus: waarom begint de grafiek niet in de
oorsprong? waarom is de grafiek eerst schuin, en daarna horizontaal?
 Hoe sterk is het magneetveld B van de permanente magneet?
15
Newton - 9 Elektromotor
§2 Magnetisch veld
Nieuwe begrippen
Magneetveld stroomdraad
Rechterhandregel bij een
stroomdraad
Ontdekken
Wat gaan we doen?
De Lorentzkracht werkt op een elektrische stroom binnen een magnetisch
veld. Dat geldt zowel voor een rechte draad als voor een draad die gewikkeld
is als een spoel. Dat betekent feitelijk dat er bij een rechte stroomdraad ook
een magnetisch veld moet zijn.
Het magnetisch veld van een stroomspoel lijkt sterk op het veld van een
staafmagneet, met een noordpool en een zuidpool. Het magnetisch veld bij
een rechte stroomdraad zal natuurlijk een andere vorm hebben.
 Welke vorm heeft het magnetisch veld van een stroomdraad?
 Heeft het magnetisch veld van een rechte stroomdraad ook een noord- en
een zuidpool?
 Op welke manier oefenen twee stroomdraden een kracht uit op elkaar?
Magneetveld en stroomdraad (kernstof, blz. 22 en 23 in Newton)
Een elektrische stroom door een spoel veroorzaakt een magnetisch veld. Als
de draad uitgerold wordt moet er nog steeds een magnetisch veld zijn.
Normaal gesproken merken we daar niets van omdat het veld te zwak is,
maar het veld is wel zichtbaar te maken.
 Schets in de linker tekening hoe de magnetische veldlijnen rond een rechte
stroomdraad lopen. Geef ook de richting van de veldlijnen aan.
 Hoe verandert het magneetveld als de richting van de elektrische stroom
omgekeerd wordt?
 Waar zitten bij een rechte stroomdraad de noord- en de zuidpool?
I
In de rechter figuur zie je een stroomdraad die gebogen is in de vorm van een
grote ring. In de tekening is de richting van de elektrische stroom
aangegeven. Dicht bij de draad zijn de magnetische veldlijnen cirkels. In de
figuur zijn enkele veldlijnen getekend.
 Geef in de tekening de richting van het magnetisch veld aan.
Omdat de ring ook de vorm heeft van een spoel (van één winding) moet het
magneetveld ook lijken op het magneetveld van een spoel.
 Teken ook enkele veldlijnen die verder van de draad liggen. Klopt deze
tekening ook met de rechterhandregel bij een spoel?
De figuren zijn in 3D
getekend, vergelijkbaar
met het assenstelsel en
de kubus
16
Verdieping
Grootheden & eenheden
De Lorentkracht tussen
twee evenwijdige rechte
stroomdraden is lang
gebruikt als definitie voor
de stroomsterkte en de
sterkte van een
magneetveld. Tussen
twee stroomdraden op 1
meter afstand met een
stroom van 1 ampère
werkt een kracht van
2,0∙10-7 N.
Twee stroomdraden
Het verschijnsel elektromagnetisme is al vrij lang bekend. In eerste instantie
werd ontdekt dat twee elektriciteitsdraden elkaar kunnen aantrekken of
afstoten, afhankelijk van de richting van de stroom in de draden. Men had
toen nog geen idee waardoor die kracht veroorzaakt werd, maar dat
veranderde toen ontdekt werd dat ook een magneet een kracht op de draad
kon uitoefenen (dat was natuurlijk de Lorentzkracht).
 Hoe kun je met behulp van magnetisme uitleggen dat twee
elektriciteitsdraden elkaar kunnen aantrekken of afstoten?
In figuur 28 zie je twee evenwijdige draden waar een elektrische stroom
doorheen loopt. Op de rechterdraad is punt P getekend. In dat punt is het
magnetisch veld van de linkerdraad ‘voelbaar’.
 Teken in de onderstaande tekening met magneetveld van de linker
stroomdraad. Geef ook de richting van het veld aan.
P
 Schets in punt P de richting van de stroomsterkte I en de richting van de
magnetische inductie B (van de linker stroomdraad).
 In welke richting werkt de Lorentzkracht in punt P?
 In welke richting werkt de Lorentzkracht op de linkerdraad?
De figuren zijn in 3D
getekend, vergelijkbaar
met het assenstelsel en
de kubus
Theorie
Lees de theorie op blz. 22 en 23 in Newton. Om de kern van de theorie goed
samen te vatten maken we gebruik van begrippen- en formuleschema’s.
Rechterhandregel bij
stroomdraad
14
Opgaven
In figuur 13 is het veldlijnenpatroon van een rechte stroomdraad getekend.
Bepaal de richting van de stroom in de draad.
17
15
Een lange stroomdraad loopt door een homogeen magnetisch veld, zoals
weergegeven in figuur 14. De richting van de stroom is loodrecht het papier
in (naar achteren). Het homogeen magnetisch veld heeft een magnetische
inductie van 2,50 mT. In de draad loopt een stroom met een stroomsterkte
van 40 A.
a Schets in figuur 14 enkele veldlijnen van het magnetisch veld van de
stroomdraad.
Op een afstand van 3,2 mm van de draad is de veldsterkte van de draad
precies 2,50 mT, even groot als het homogene veld.
b Geef in die schets een punt P aan waar de totale magnetische inductie nul
zou kunnen zijn.
c Hoe groot is de magnetische inductie in een punt Q tegenover P en op
gelijke afstand van de stroomdraad?
16
Bepaal de richting van de Lorentzkracht in punt P op de rechterdraad in elk
van de drie situaties van figuur 29 (bij B en C loopt de schuin getekende
draad naar achteren).
17
Motor
De `sterkte' van een elektromotor wordt bepaald door verschillende
eigenschappen van de motor:
- de lengte l en breedte b van de spoel
- het aantal windingen
De stroomsterkte door de spoel hangt af van:
- de spanning waarop de motor wordt aangesloten
- de weerstand van de draden van de spoel
a Beschrijf welke invloed de lengte l en de breedte b van de spoel hebben op
de ‘sterkte’ van de spoel.
De figuur is in 3D
getekend, vergelijkbaar
met het assenstelsel en
de kubus
b Leg uit dat een motor met een spoel met een groot aantal windingen
gemaakt van dun koperdraad niet ‘sterker’ hoeft te zijn dan een motor
met een spoel met een klein aantal windingen gemaakt van dik
koperdraad.
18
Het aantal windingen N van de rotorspoel is 600. Elke winding heeft een
breedte b van 2,5 cm en een lengte l van 3,5 cm. De rotorspoel is gemaakt
van koperdraad met een dwarsdoorsnedeoppervlak A van 0,15 mm².
c Bereken de weerstand van de koperdraad van de spoel.
De magnetische inductie B van het statorveld is 0,085 T. De rotorspoel wordt
aangesloten op een spanning U van 6,0 V.
d Bereken de Lorentzkracht op één zijde van de rotorspoel.
18
Lanceerinrichting
Lees eerst het onderstaande tijdschriftartikel over een elektromagnetische
lanceerinrichting en probeer daarna een antwoord op de vraag te vinden.
Lancering zonder explosie
Aan de Technische Universiteit van Delft
is men er in geslaagd een
lanceerinrichting te ontwikkelen die geen
gebruik maakt van een explosie. Het
projectiel wordt weggeschoten door
middel van de Lorentzkracht. Het gaat
hier om een zogenaamde Single Pulse
Rail Accelerator.
Het apparaat bestaat uit een
rechthoekige goot. De twee zijwanden
zijn van metaal. De bodem is gemaakt
van isolerend materiaal. De

Lorentzkracht wordt opgewekt door een
sterke stroom van 1,7 MA die via de
zijwanden door het projectiel gaat. Het
metalen projectiel maakt tijdens het
afschieten steeds contact met de
zijwanden. Boven en onder de goot zijn
twee grote spoelen opgesteld die een
homogeen magnetisch veld opwekken
met een sterkte van 2,5 T. Bij het
afschieten wordt op het projectiel van 80
g gedurende 2,0 ms een kracht van 85
kN uitgeoefend.
Is de in het artikel genoemde kracht van 85 kN op het projectiel in
overeenstemming met de rest van de gegevens, en welke snelheid zou het
projectiel daardoor bij verwaarloosbaar kleine wrijvingskrachten
krijgen?
19
19
Zonneauto
In november 1987 werd dwars door Australië een race gehouden voor auto's
die de zon als energiebron gebruiken. Een van die auto's bestond voor het
grootste deel uit een paneel zonnecellen met een oppervlak van 8,0 m². Het
vermogen van de zonnestraling in Australië bedraagt gemiddeld zo'n 1000
W/M² gedurende 12 uur per dag. Het zonnepaneel levert per dag ongeveer
14 kWh elektrische energie aan de elektromotor. De gemiddelde snelheid van
deze zonneauto is 70 km/h. Bij die snelheid heeft de tegenwerkende
wrijvingskracht (rol- en luchtwrijving) een waarde van 50 N.
 Hoe groot is het rendement van het systeem voor de voortstuwing van
deze zonneauto?
20
Newton - 10 Dynamo en transformator
§2 Inductiespanning
Nieuwe begrippen
Inductiespanning
Inductiestroom
Wet van Lenz
Magnetische flux
Ontdekken
Wat gaan we doen?
Een dynamo bestaat uit dezelfde onderdelen als een elektromotor: een spoel
en een magneet. Bij een dynamo ontstaat een spanning als de spoel of de
magneet bewogen wordt. Kennelijk zorgt een bewegende magneet of een
veranderend magneetveld voor een elektrische spanning die we
inductiespanning noemen. Door die spanning kan er ook een inductiestroom
gaan lopen.
 In welke richting loopt de inductiestroom?
 Hoe groot is de inductiespanning?
Dynamo: een spoel en een magneet (context)
Op de onderstaande afbeeldingen is te zien dat er twee types zijn: met een
bewegende magneet of met een bewegende spoel.
Bij een fietsdynamo draait een magneet tussen twee spoelen, maar er zijn ook
dynamo’s waarbij een spoel tussen twee magneten draait.
Op de onderstaande afbeeldingen zijn drie ‘dynamo’s’ te zien: een schudzaklantaarn, een microfoon en de elektromotor/dynamo uit een Honda Civic.
 Wat beweegt er bij elk van deze dynamo’s, de magneet of de spoel(en)?
Luidspreker als microfoon
Net als een dynamo lijkt op een elektromotor, zo lijkt een luidspreker op een
microfoon.
 Leg uit hoe deze simpele intercom kan werken zonder spanningsbron.
 Kun je een elektromotor en een dynamo net zo aan elkaar koppelen als deze
intercom?
21
Demonstratie
Applet
Bekijk de werking van een
dynamo en het principe
van inductie met de
applets van PhET.
Elektromagnetische inductie (kernstof, Newton blz. 38 t/m 44)
Bekijk de demonstratie (en eventueel de applets) over het verschijnsel van
elektromagnetische inductie.
 In welke richting loopt de elektrische stroom in de spoel als de magneet
naar de spoel toe beweegt? (zie demonstratie of applet).
 In welke richting loopt de elektrische stroom in de spoel als de magneet van
de spoel af beweegt?
De inductiestroom in de spoel zorgt voor een magneetveld.
 Laat zien dat daardoor in beide gevallen de beweging wordt tegengewerkt.
Het verschijnsel elektromagnetische inductie treedt ook op bij twee spoelen
op het moment dat de elektrische stroom in één van de spoelen verandert.
 Teken de richting van het magneetveld van de linker spoel als de schakelaar
gesloten is (kijk goed hoe de spoel gewikkeld is).
Op het moment dat de schakelaar gesloten wordt gaat in de rechter spoel een
inductiestroom lopen. Het magneetveld werkt het ontstaan van de inductie
tegen.
 Teken de richting van de inductiestroom en de richting van het
magneetveld dat daardoor ontstaat.
 Leg uit dat er ook een inductiestroom gaat lopen op het moment dat de
schakelaar geopend wordt.
 Leg uit dat de richting van de elektrische stroom nu tegengesteld is.
Vervolgopdracht
De grootte van de inductiespanning
Het verschijnsel inductie houdt in dat een veranderend magneetveld door
een spoel of winding een inductiespanning veroorzaakt. De grootte van de
inductiestroom hangt ook af van de weerstand van de kring.
De grootte van de inductiespanning hangt af van de volgende grootheden:
 De sterkte en richting van het magneetveld.
 De snelheid waarmee de sterkte van het magneetveld verandert.
 Het aantal windingen van de spoel.
 Het oppervlak van de winding (of de doorsnede van de spoel)
Lees de theorie in Newton (blz. 38 t/m 45) en beantwoord de volgende
vragen:
 Hoe is de invloed van de bovenstaande grootheden zichtbaar in de twee
formules (over magnetische flux en inductiespanning)?
 Beschrijf in je eigen woorden wat we met de magnetische flux Φ bedoelen.
22
Theorie
Lees de theorie op blz. 36 t/m 46 in Newton. Om de kern van de theorie goed
samen te vatten maken we gebruik van begrippen- en formuleschema’s.
Magnetische flux
Inductiespanning,
inductiestroom
Wet van Lenz
Tegenflux / meeflux
Formulelijst
Noteer bij de onderstaande formules: - Wat betekent elk symbool? - Welke
eenheid hoort bij elk symbool? - Wanneer kun je de formule toepassen?
  B  A  cos   Bn  A
U ind  N 

t
Opgaven
20 Elektromagnetische inductie
Met een magneet in de buurt van een spoel zoals in figuur 2 kun je over de
uiteinden van de spoel een spanning opwekken. Deze spanning noemen we
de inductiespanning.
a Als je de magneet en de spoel alleen maar bij elkaar in de buurt houdt, gebeurt er niets: er ontstaat geen inductiespanning over de uiteinden van de
spoel. Wat moet je doen om een inductiespanning op te wekken?
b Hoe verandert de inductiespanning bij het afwisselend naar de spoel toe
en van de spoel af bewegen van de magneet? En bij het ronddraaien van
de magneet in de buurt van de spoel?
c In figuur 3 is weergegeven hoe een (eenvoudige) microfoon is
opgebouwd: een trilplaatje met daaraan vast een spoel in de buurt van
een magneet. Op welke manier zet deze microfoon geluid om in een
elektrisch signaal?
23
21
De elektromagneet van figuur 5 is via een schakelaar S aangesloten op een
gelijkspanningsbron. Hieronder staan vier situaties. Leg in elk van deze
situaties uit of er wel of niet een inductiespanning over de spoel ontstaat.
A De schakelaar is open en er loopt dus geen stroom door de
elektromagneet.
B De schakelaar wordt gesloten, zodat er een stroom door de
elektromagneet gaat lopen.
C De schakelaar is gesloten en er loopt een stroom door de elektromagneet.
D De schakelaar wordt geopend, zodat de stroom door de elektromagneet
wordt verbroken.
22
De elektromagneet van figuur 6 is aangesloten op een regelbare
wisselspanningsbron.
a Over de spoel staat een inductiespanning. Leg uit waarom.
b Deze inductiespanning over de spoel is een wisselspanning. Leg uit
waarom.
c De spanning van de wisselspanningsbron wordt ingesteld op een hogere
waarde. Hoe verandert daardoor de inductiespanning over de spoel?
d De snelheid waarmee de polen van de wisselspanningsbron van teken
wisselen wordt op een hogere waarde ingesteld. Hoe verandert daardoor
de inductiespanning over de spoel?
23
Bij verkeerslichten zit soms een grote spoel met enkele windingen in het weg
dek. Zo'n spoel wordt een inductielus genoemd.
a Wat is de functie van zo'n inductielus?
b Wanneer geeft zo'n inductielus een spanningspuls: als er een auto
overheen rijdt of als er een auto boven stilstaat?
c Hoe komt het eigenlijk dat de inductielus een spanningspuls afgeeft: een
auto is toch geen magneet?
24
Newton - 10 Dynamo en transformator
§2 Inductiespanning
Wat gaan we doen?
Een dynamo bestaat uit dezelfde onderdelen als een elektromotor: een spoel
en een magneet. In de voorgaande voorbeelden was er steeds sprake van een
stilstaande spoel en een bewegende magneet (of een veranderend
magneetveld). Hoe werkt een dynamo waarbij de spoel beweegt?
 In welke richting loopt de inductiestroom?
 Hoe groot is de inductiespanning?
Ontdekken
De werking van een dynamo (kernstof, Newton blz. 47 t/m 49)
Op de figuur hiernaast is een dynamo afgebeeld met ronddraaiende spoel
(maar het kan natuurlijk net zo goed een afbeelding van een elektromotor
zijn). De sterkte en richting van het magneetveld zijn constant.
 Welke richting heeft het magneetveld door de spoel?
 Als de spoel draait dan verandert de sterkte van het magneetveld niet. Leg
uit dat er dan toch een inductiespanning ontstaat. Gebruik in je antwoord
het begrip flux.
 Stel dat de spoel in de tekening linksom draait (tegen de klok in). In welke
richting loopt dan de inductiestroom in punt S. Leg duidelijk uit en gebruik
in je antwoord het begrip flux.
De richting van de elektrische stroom is ook goed te controleren met behulp
van de Lorentzkracht. De spoel wordt in beweging gebracht door een
uitwendige kracht (linksom) en daardoor ontstaat een inductiestroom.
Omdat die stroom zich in een magneetveld bevindt moet er ook een
Lorentzkracht werken. Die kracht moet bovendien de oorzaak van de
inductie tegenwerken en dus moet de Lorentzkracht tegengesteld zijn aan de
bewegingsrichting.
 Controleer in dit voorbeeld dat de Lorentzkracht de beweging tegenwerkt.
De grootte van de inductiespanning
Een rechthoekige spoel draait rond in een homogeen magnetisch veld (zie
figuur). De maximale magnetische flux Φmax door de winding bedraagt 60
μWb (in de loodrechte stand). Als de spoel draait dan verandert de flux, de
flux hangt af van hoek α (zie tekening).
 Leg uit dat geldt Φ = Φmax∙sin(α)
25
Grootheden & eenheden
De spoel wordt met een constante snelheid rondgedraaid. In de
onderstaande grafiek is weergegeven hoe de flux door de spoel verandert in
de loop van de tijd.
De eenheid voor
magnetische flux is
Weber. De eenheid wordt
bepaald door de formule
Daaruit volgt dat 1 weber
gelijk is aan 1 T × 1 m², of
andersom:
T = Wb/m².
70
60
50
40
flux (μWb)
  B A
Magnetische flux door spoel
30
20
10
0
-10
uit de formule voor
inductiespanning volgt
overigens ook nog dat:
V = Wb/s
0
0,005
0,01
0,015
0,02
0,025
-20
tijd t (s)
De spoel heeft 600 windingen. In de grafiek is een raaklijn getekend op het
tijdstip t = 0,0060 s.
 Leg uit dat je de inductiespanning op dit tijdstip kunt berekenen met behulp
van de helling van de raaklijn.
 Bepaal de helling van de raaklijn en bereken daarmee de inductiespanning
op dit tijdstip.
Verdieping (NT)
Een formule voor de dynamospanning
De spoel van de dynamo draait met constante snelheid rond.
 Bepaal uit de bovenstaande grafiek de omwentelingstijd en bereken
daarmee de frequentie waarmee de spoel ronddraait.
 Controleer dat voor deze grafiek geldt:
(t )   max  sin( 2  f  t ) .
 Bepaal de afgeleide Φ’(t) en bereken daarmee de maximale
inductiespanning.
De richting van de inductiestroom
In de figuur is de richting van het magneetveld en de richting waarin de
spoel ronddraait getekend. Bovendien is de richting van de elektrische
stroom getekend.
 Verklaar de richting van de inductiestroom met de wet van Lenz.
 Controleer de richting van de inductiestroom door de richting van de
Lorentzkracht te tekenen. Verklaar vervolgens waarom de Lorenstkracht
altijd tegengesteld aan de beweging moet zijn.
26
Opgaven
24
Binnen een spoel met 150 windingen verandert de magnetische flux  als
functie van de tijd t zoals weergegeven in het diagram van figuur 11.
a Teken in een (Uind,t)-diagram de inductiespanning over de spoel als
functie van de tijd.
b Geef een toelichting bij het getekende verloop van de inductiespanning.
Ga daarbij in op zowel de grootte als het teken van de inductiespanning.
25
Binnen een spoel met 1200 windingen verandert de magnetische flux  als
functie van de tijd t zoals weergegeven in het diagram van figuur 12.
a Teken in een (Uind,t)diagram de inductiespanning over de spoel als
functie van de tijd.
b Geef een toelichting bij het getekende verloop van de inductiespanning.
Ga daarbij in op zowel de grootte als het teken van de inductiespanning.
26
Binnen een spoel met één winding
verandert de magnetische flux  als
functie van de tijd t zoals weergegeven in
het diagram van figuur 13. Leg uit op welk
tijdstip de inductiespanning over de spoel
maximaal is. Bepaal deze maximale
waarde van de inductiespanning.
27
Newton - 10 Dynamo en transformator
§2: Inductiespanning
Toepassing
De vallende magneet
De uiteinden van een verticaal opgestelde spoel zijn aangesloten op een
oscilloscoop. Boven de spoel wordt een staafmagneet losgelaten. De magneet
valt door de spoel.
Op het scherm van zo'n oscilloscoop wordt dan de spanning over de spoel
weergegeven als functie van de tijd. Er zijn twee in de tijd opeenvolgende
spanningspulsen te zien, zoals weergegeven in de grafiek.
Uind (V)
t (ms)
De eerste puls ontstaat op het moment dat de magneet de spoel binnengaat,
de tweede puls ontstaat als de magneet uit de spoel komt. De twee pulsen
lijken wel op elkaar, maar er zijn toch verschillen.
 Verklaar de volgende verschillen:

De 2e puls is smaller dan de 1e puls

De 2e puls is hoger (dieper) dan de 1e puls

De 2e puls is positief, de 1e puls is negatief
 Tijdens het vallen wordt de magneet door de spoel afgeremd. Hoe kan dat?
Verdieping (NT)
Oppervlakte
De tweede puls is smaller en hoger dan de 1e puls. De hoogte van de puls
wordt bepaald door de formule:
U ind  N 

 N   ' (t )
t
 Leg met behulp van de theorie uit dat de oppervlakte van beide pulsen even
groot zou moeten zijn.
 Stel dat je het aantal windingen N en de oppervlakte A van de doorsnede
van de spoel zou weten. Hoe zou je dan met behulp van de grafiek een
schatting van de sterkte van het magneetveld kunnen maken?
28
Opgaven
27
Een spoel met 100 windingen en een dwarsdoorsnedeoppervlak A van 6,0
cm² bevindt zich in een homogeen magnetisch veld met een magnetische
inductie B van 3,0 mT. In de beginstand valt de lengteas van de spoel samen
met de richting van de veldlijnen.
a Bereken de grootte van de magnetische flux door de spoel.
De spoel wordt in 0,10 s vanuit de beginstand een halve slag (dus: over 180º)
gedraaid, zodat de lengteas van de spoel weer samenvalt met de richting van
de veldlijnen. Vanuit de draaiende spoel gezien is de richting van de omvatte
magnetische veldlijnen in de begin- en eindstand tegengesteld.
b Bereken de gemiddelde inductiespanning tijdens het draaien.
28 De elektromagneet van figuur 14 is aangesloten op een regelbare
gelijkspanningsbron. De spanning van de gelijkspanningsbron wordt
geleidelijk groter gemaakt.
a Bepaal de richting van de inductiestroom in de spoel.
De spoel is op te vatten als een spanningsbron waarop bijvoorbeeld een
lampje kan branden (in de figuur is een weerstand getekend).
b Geef in de tekening aan wat de plus- en min-pool van deze spanningsbron
is.
29
Een spoel met één vierkante winding wordt met een constante snelheid van
links naar rechts door een homogeen magnetisch veld bewogen, zoals
weergegeven in figuur 15. Het magnetisch veld is alleen aanwezig in het
gerasterde deel van de ruimte, en het veld is loodrecht naar achter gericht
(het papier in)
In de grafiek is een (,t)-diagram van de magnetische flux getekend.
a Teken in de onderstaande figuren de richting van de inductiestroom.
29
b Als er een inductiestroom in de spoel loopt, wordt op de zijden van de
spoel in het magnetisch veld een Lorentz-kracht uitgeoefend. Teken deze
Lorentz-kracht in de figuren.
c Welke invloed heeft deze Lorentz-kracht op de beweging van de spoel? Is
dit in overeenstemming met de wet van Lenz? Leg uit waarom wel of niet.
30 Fietsdynamo
Een fietsdynamo bestaat uit een ronddraaiende magneet in de buurt van een
spoel, zoals schematisch weergegeven in figuur 20. In de onderstaande
grafiek is de flux door de spoel als functie van de tijd weergegeven. Een flux
naar rechts is hierbij als positief weergegeven.
a Leg uit dat de stand van figuur 20 overeen komt met t = 0.
b Geef in de grafiek het tijdstip weer dat de magneet een kwartslag gedraaid
is (dus: over 90°).
c Bepaal de richting van de inductiestroom tijdens de eerste kwartslag.
d Leg met behulp van de grafiek uit dat de inductiestroom tijdens de tweede
en derde kwartslag in de andere richting loopt.
e Op welk tijdstippen is de inductiespanning maximaal? Geef die
momenten in de grafiek aan.
f
Schets in de onderstaande grafiek een (Uind,t)-diagram van de
inductiespanning als functie van de tijd. De maximale inductiespanning is
1,2 V. Tijdens de eerste kwartslag is de inductiespanning negatief.
g De magneet wordt met een tweemaal zo kleine snelheid rondgedraaid.
Schets in hetzelfde diagram (met een andere kleur) weer de
inductiespanning als functie van de tijd.
30
Newton - 10 Dynamo en transformator
§3 Elektriciteitsvoorziening
Wat gaan we doen?
Het elektriciteitsnet levert wisselspanning. De grafiek van de spanning en de
stroomsterkte heeft dan de vorm van een sinusfunctie. De grootte van de
spanning en de stroomsterkte verandert dus voortdurend. Dat betekent dat
ook het elektrisch vermogen P niet constant is.
 Hoe groot is de maximale spanning en stroomsterkte?
Ontdekken
Hoe groot is de maximale spanning? (kernstof, Newton blz. 51 en 52)
De netspanning in huis is een wisselspanning van 230 volt met een
frequentie van 50 Hz. De spanning wordt dus per seconde 50 keer positief en
50 keer negatief. De 230 volt is een soort gemiddelde spanning, we noemen
het de effectieve spanning Ueff.. Voor de netspanning geldt dus:
effectieve spanning Ueff = 230 volt
frequentie
f = 50 Hz.
Op de netspanning wordt een elektrische kachel aangesloten met een
vermogen van 600 watt.
 Ga na dat de effectieve stroomsterkte 2,6 A is.
De spanning en de stroomsterkte zijn bij wisselspanning een sinusfunctie:
U  U max  sin( 2  f  t ) en I  I max  sin( 2  f  t )
Voor de maximale spanning en stroomsterkte geldt:
U max   2  U eff
I max   2  I eff
en
 Bereken voor de elektrische kachel de maximale spanning en de maximale
stroomsterkte.
Waar komt de factor 2 vandaan?
De elektrische kachel heeft een effectief vermogen van 600 watt. De
effectieve stroomsterkte is 2,6 A. Voor het vermogen geldt: P = UI.
Met de grafische rekenmachine zijn de grafieken van de spanning en de
stroomsterkte te tekenen. De frequentie f van de spanning is 50 Hz.
U = Umax∙sin(2∙f∙t)
wordt
Y1 = 230*sin(100x)
I = Imax∙sin(2∙f∙t)
wordt
Y2 = 2.6*sin(100x)
window:
x van 0 tot 0,04
y van -50 tot 50
 Teken beide grafieken met de GR. (zet wel de GR in [MODE - RADIAN] ) en
controleer dat de periode 1/50e seconde is.
 Teken de grafiek van het vermogen P als Y3 = Y1×Y2. Ga na dat de grafiek
hetzelfde is als de onderstaande grafiek. Pas het window aan.
31
 Hoe groot is het maximale vermogen?
 Laat zien dat Pmax = UmaxImax.
De elektrische kachel heeft een effectief vermogen van 600 watt. Dat
betekent dat het gemiddelde vermogen 600 watt is.
 Laat met behulp van de oppervlakte onder de grafiek zien dat het
gemiddelde vermogen 600 watt is.
Kennelijk geldt altijd: Pmax  2  Peff
 Kun je nu in je eigen woorden uitleggen waarom er in de formules voor de
maximale spanning en stroomsterkte een factor
2 zit?
Theorie
Bestudeer de theorie van de dynamo, blz. 47 t/m 52 in Newton. Controleer of
je onderstaande begrippen goed begrijpt. Maak zonodig aantekeningen of
een schetsje in de rechterkolom.
Wisselspanningsbron
Effectieve
spanning/stroomsterkte
Formulelijst
Noteer bij de onderstaande formules: - Wat betekent elk symbool? - Welke
eenheid hoort bij elk symbool? - Wanneer kun je de formule toepassen?
U (t )  U max  sin( 2  f  t )
I (t )  I max  sin( 2  f  t )
U max   2  U eff
I max   2  I eff
Pmax  2  Peff
32
31
Opgaven
Een dynamo wordt aangedreven door een gewichtje dat aan een touwtje naar
beneden valt. Het gewichtje heeft een massa van 0,65 kg. Het gewichtje daalt
met een constante snelheid over een afstand van 1,0 m in een tijd van 4,7 s.
Voor de arbeid die de zwaartekracht verricht geldt: W  Fz  s .
a Bereken de arbeid van de zwaartekracht.
De dynamo is aangesloten op een lamp met een weerstand van 30 . De
dynamo levert een effectieve spanning van 5,7 V over de lamp.
b Bereken de stroomsterkte en het vermogen.
c Bereken hoeveel elektrische energie de dynamo levert in de tijd dat het
gewichtje valt.
d Bereken het rendement van de dynamo.
32 Dynamospanning
De rotorspoel van een dynamo heeft 400 rechthoekige windingen van 2,5 bij
3,5 cm. De magnetische inductie B van het statorveld is 85 mT. De dynamo
draait met een toerental n van 50 omwentelingen per seconde.
a Bereken de maximale flux door de spoel.
b Bereken U ind  N 

met Δt de tijd waarin de flux verandert van de
t
maximale flux naar de minimale flux (maximaal de andere kant op).
33
33
Afvalscheiding
Lees eerst het onderstaande krantenartikel. Geef daarna antwoord op de
vragen die onder het artikel staan.
Magneet laat aluminium eruit springen
de Volkskrant, 1995
Aluminium in huishoudelijk afval
gaat
ten
dele
verloren
op
stortplaatsen
of
in
verbrandingsovens. Dit is zonde,
gezien de hoge marktwaarde van
dit opnieuw bruikbare materiaal.
Als het afval over de band loopt, blijft
eventueel aanwezig ijzer aan de koprol
plakken totdat het aan de onderkant
door de zwaartekracht los laat. Niet
metaalhoudende materialen vallen aan
het einde van de band naar beneden,
terwijl aluminium naar voren wordt
weggeschoten. Uiteindelijk ontstaan er
dus drie verschillende fracties.
In het afval zit twintigduizend ton
aluminium,
met
een
potentiële
marktwaarde van twintig miljoen
gulden. Terugwinning is niet alleen
economisch interessant. Aluminium kan
keer op keer worden gerecycled, wat
slechts vijf procent kost van de energie
die nodig is voor de productie van
aluminium uit bauxiet.
Aluminium laat zich niet zoals ijzer door
een
magneet
aantrekken.
De
afvalverwerkingsinstallaties
maken
daarom
gebruik
van
een
wervelstroomscheider. Dit apparaat
bestaat uit een transportband met in het
uiteinde - de koprol - een snel draaiende
rotor die is voorzien van magneten.
Deze magneten staan om en om met
hun noord- of zuidpool naar buiten
gericht.
Wervelstroomscheider haalt aluminium uit afval. Snel roterende magneten in de
koprol staan om en om met hun noord- of zuidpool naar buiten gericht en
veroorzaken wervelstromen in het aluminium, waardoor het metaal het magneetveld
probeert te ontwijken en van de band schiet.
In het artikel is sprake van een wervelstroomscheider voor het 'wegschieten'
van aluminium. Met de opstelling van figuur 24 is dit effect in een
vereenvoudigde situatie te demonstreren. Naast de spoel met een
weekijzeren kern hangt een aluminium ring. Deze ring kun je opvatten als
een spoel met één winding, waarvan de uiteinden zijn kortgesloten.
a Leg uit waarom aluminium niet met een (elektro-)magneet uit de
afvalstroom te scheiden is.
b In de opstelling van figuur 24 is de schakelaar S geopend. Bij het sluiten
van deze schakelaar wordt de ring afgestoten door de spoel. Verklaar dit.
c Leg uit waarom de koprol van de wervelstroomscheider bestaat uit snel
roterende magneten die om en om met hun noord- of zuidpool naar
buiten gericht zijn.
34
34
Dynamorendement
Voor het bepalen van het rendement van een fietsdynamo moet het aan de
dynamo geleverde mechanisch vermogen bekend zijn. Het dynamowiel
wordt aangedreven door een fietswiel. Daarbij oefent het fietswiel een kracht
F uit op het dynamowiel.
De fietsdynamo wordt aangedreven door een fietswiel met een omtrek van
217 cm. Het toerental van het fietswiel is 2,0 omwentelingen per seconde. Bij
dit toerental oefent het fietswiel een kracht van 1,20 N uit op het
dynamowiel.
a Bereken de arbeid die het fietswiel per seconde levert aan de dynamo.
In deze situatie levert de dynamo een spanning van 6,0 V. De koplamp en het
achterlicht van de fiets zijn aangesloten op deze dynamospanning. In de
koplamp zit een lampje van 6,0 V-0,4 A, in het achterlicht een lampje van
6,0 V-0,05 A.
b Bereken hoeveel elektrische energie de dynamo per seconde levert.
c Bereken het rendement  van de dynamo.
35
Newton - 10 Dynamo en transformator
§3 Elektriciteitsvoorziening
Wat gaan we doen?
Een transformator verandert de spanning. Transformatoren kom je op zeer
veel plaatsen tegen. Alle huishoudelijke apparaten die op een lagere
spanning werken, zoals b.v. een computer, gebruiken een transformator of
een adapter (een adapter maakt van wisselspanning ook nog gelijkspanning).
 Hoe werkt een transformator?
 Hoe bepaal je de factor waarmee de spanning verhoogd of verlaagd
wordt?
Ontdekken
Transformator (kernstof, Newton blz. 57 t/m 59)
Een transformator is eenvoudig apparaat: het bestaat uit een weekijzeren
kern en twee spoelen. Je kunt ermee de spanning verhogen of verlagen door
verschillende spoelen te nemen.
 Leg uit dat een transformator alleen op wisselspanning kan werken.
Ideale transformator
Bij een ideale transformator gaat er geen energie verloren (bijvoorbeeld door
warmte-ontwikkeling in de spoelen). De uitgangsspanning Us van een ideale
transformator hangt af van de verhouding van het aantal windingen van de
primaire spoel en de secundaire spoel. Als het aantal windingen gelijk is dan
is de uitgangsspanning Us gelijk aan de ingangsspanning Up.
 Bij welke van de twee bovenstaande transformatoren is de
uitgangsspanning Us hoger dan de ingangsspanning Up?
 Leg in je eigen woorden uit waardoor de uitgangsspanning Us groter wordt
als de secundaire spoel meer windingen heeft.
 Met welke factor wordt de spanning in de twee bovenstaande voorbeelden
veranderd?
36
Spanning en stroomsterkte
Een transformator verandert de spanning, maar wat gebeurt er eigenlijk met
de stroomsterkte? Dat moet in elk geval ook afhangen van het apparaat dat
aan de secundaire kant wordt aangesloten. De stroomsterkte in de
secundaire kring Is wordt bepaald door de secundaire spanning Us en de
weerstand van het apparaat, gewoon volgens U = I∙R.
De stroomsterkte in de primaire kring wordt niet bepaald door de
netvoeding maar door het apparaat dat aan de secundaire kring wordt
aangesloten en door de verhouding van de windingen van de spoel.
Bij een ideale spoel gaat geen energie verloren.
 Leg in je eigen woorden uit dat de primaire stroomsterkte niet gelijk kan
zijn aan de secundaire stroomsterkte
 Leg uit dat bij een ideale spoel moet gelden: Up∙Ip = Us∙Is
In de transformator op de afbeelding heeft de primaire spoel 20 windingen
en de secundaire spoel 8 windingen. De transformator wordt aangesloten op
een wisselspanning van 120 volt.
 Hoe groot is dan de secundaire spanning?
Op de secundaire spoel wordt een apparaat aangesloten met R = 20 Ω.
 Bereken de secundaire stroomsterkte en de primaire stroomsterkte.
Rendement (kernstof, Newton blz. 33, 34, 52, 53, 58 en 59)
De drie belangrijkste toepassingen van elektromagnetisme zijn de
elektromotor, de dynamo en de transformator. Deze drie apparaten zijn ook
energieomzetters. Met het rendement van een apparaat wordt bedoeld
hoeveel procent van de gebruikt energie wordt omgezet in nuttige energie.
Bij de elektromotor en de dynamo zijn de energiesoorten elektrische energie
en arbeid.
 Bij welk apparaat hoort de formule

W
?
Eelektr
 Bij welk apparaat hoort de formule

Eelektr
?
W
 Leg uit dat je bij het berekenen van het rendement ook het gebruikte
vermogen en het nuttige vermogen kunt gebruiken.
 Met welke formule kun je het mechanisch vermogen P m uitrekenen?
Bij een transformator kun je het rendement ook uitdrukken in spanning en
stroomsterkte.
 Schrijf de formule voor het rendement van een transformator met behulp
van spanning en stroomsterkte.
37
Theorie
Bestudeer de theorie van de transformator, blz. 57 t/m 59 in Newton.
Controleer of je onderstaande begrippen goed begrijpt. Maak zonodig
aantekeningen of een schetsje in de rechterkolom.
Transformatorverhouding
Ideale transformator
Formulelijst
Noteer bij de onderstaande formules: - Wat betekent elk symbool? - Welke
eenheid hoort bij elk symbool? - Wanneer kun je de formule toepassen?
Up
Us

Np
Ns
U p  I p Us  Is
35
36
Opgaven
Een apparaat (bijvoorbeeld een walk- of discman, of de printer van een
computer) is via een adapter aangesloten op de netspanning. Het apparaat is
uitgeschakeld, maar de adapter zit nog steeds in het stopcontact. Wordt er in
deze situatie elektrische energie verbruikt? Leg uit waarom wel of niet.
Een 12 V-20 W halogeenlamp wordt via een (ideale) transformator
aangesloten op de netspanning van 230 V. De secundaire spoel heeft 300
windingen.
a Bereken het aantal windingen dat de primaire spoel moet hebben om de
halogeenlamp op de juiste spanning te laten werken.
b Hoe groot is de secundaire stroomsterkte? En de primaire stroomsterkte?
c De halogeenlamp wordt vervangen door een 12 V-50 W halogeenlamp. Is
er nu een andere transformator nodig? Leg uit waarom wel of niet.
38
37
Een transformator is aangesloten op de netspanning. Het resultaat van de
metingen van de primaire en secundaire spanning en stroomsterkte met een
wisselspannings- en wisselstroommeter is weergegeven in de tabel van figuur
27.
 Bereken het rendement van de transformator.
38 Een transformator met een primaire spoel van 4400 windingen is
aangesloten op de netspanning. Het door de transformator opgenomen
vermogen is 18 W. Op de secundaire spoel van 260 windingen is een lamp
aangesloten.
a Bereken de secundaire spanning.
De transformator heeft een rendement van 0,80 (of 80%).
b Bereken de stroomsterkte in de lamp.
39
Newton - 10 Dynamo en transformator
§3 Elektriciteitsvoorziening
Demonstratie
Gevaarlijke trafo’s?
In de klas staan twee opstellingen met nogal extreme transformatoren: het
aantal windingen van de secundaire spoel is zeer groot of zeer klein. Beide
opstellingen worden aangesloten op de netspanning.
Lastrafo (context, Newton blz. 60)
De primaire spoel heeft 600 windingen, de secundaire spoel heeft 5 dikke
windingen. De secundaire spoel is met een spijker kortgesloten. De primaire
spoel wordt aangesloten op 230 volt wisselspanning.
 Hoe kan deze opstelling dienen als lastrafo? Hoe kan bij zo’n kleine
spanning de spijker smelten?
Boogspanning
De primaire spoel heeft 600 windingen, de secundaire spoel heeft 18.000
windingen. Op de secundaire spoel staan twee kromme metalen bogen die
licht van elkaar af buigen. De primaire spoel wordt aangesloten op 230 volt
wisselspanning.
 Leg uit wat er gebeurt. Hoe groot wordt de spanning?
 Welke opstelling is gevaarlijk om aan te raken? Zou je dat durven?
Toepassing
Hoogspanningskabels (context, Newton blz. 65)
Om elektrische energie te transporteren van de centrale naar de woonwijken
worden hoogspanningskabels gebruikt. In Nederland werken deze kabels
met een spanning van maar liefst 110 kV. Zo’n hoge spanning is natuurlijk
ook gevaarlijk en daarom zijn er strenge veiligheidsvoorzieningen nodig.
Waarom gebruiken we eigenlijk hoogspanning om energie te transporteren?
Is het niet veel makkelijker en veiliger om een lagere spanning te gebruiken?
Een voorbeeld: Een elektriciteitscentrale moet aan een woonwijk een
vermogen van 460 kW leveren, bij een spanning van 230 V. De twee kabels
hebben elk een weerstand van 0,5 Ω.
Voor de getransporteerde energie geldt;
P = U∙I
Voor het energieverlies in de draden geldt:
P = I²∙Rdraad
 Wat is het voordeel van werken met een hoge spanning bij
energietransport?
 Wat zou er misgaan als er een lage spanning gebruikt zou worden? Geef
een toelichting met een berekening.
40
Toepassing
Aardlekschakelaar (context, Newton blz. 63)
Een aardlekschakelaar werkt ook met behulp van magnetisme. Rond een
stuk weekijzer zijn drie spoelen geplaatst. Door spoel A en B gaat de
elektrische stroom die het huis in- en uitgaat. Spoel C is aangesloten op een
relais dat de schakeling verbreekt zodra er een stroom door spoel C loopt.
 Leg uit dat in normale omstandigheden er geen magneetveld door spoel C
gaat.
 Hoe werkt deze aardlekschakelaar?
Verdieping (NT)
Veiligheidsmaatregelen (context, Newton blz. 61)
In de badkamer zit soms een speciaal scheerstopcontact. Dit stopcontact
levert normaal 230 volt, maar het is extra beveiligd. Als je één van de
contactpunten aanraakt zal er geen stroom door je lichaan gaan.
Daarnaast kunnen alleen apparaten met een klein vermogen aangesloten
worden.
In de tekening zie je hoe de veiligheidstransformator werkt.
 Waarom heeft de secundaire spoel evenveel windingen als de primaire
spoel?
 Waarom is er geen gevaar als je alleen punt A of punt B aanraakt, maar
wel als je beide punten tegelijk aanraakt?
 De secundaire spoel is gemaakt van zeer dun koperdraad. Waarom?
41
39
Variac
Een variac is een transformator waarbij met een schuifcontact S een groter of
kleiner aantal secundaire windingen is in te schakelen. Een variac is dus een
regelbare transformator.
a Bekijk figuur 31. Hoe verandert de secundaire spanning als de schuif S
omhoog geschoven wordt?
De primaire spoel heeft 440 windingen en wordt aangesloten op een
wisselspanning Up van 220 V. De secundaire spanning Us is dan met het
schuifcontact te variëren tussen 6,0 en 260 V.
b Bereken het maximale en minimale aantal windingen van de secundaire
spoel.
De variac wordt ingesteld op een secundaire spanning van 100 V. Op de
secundaire spoel wordt een 230 V-60 W lamp aangesloten. De secundaire
stroomsterkte Is wordt gemeten: Is = 0,179 A.
c Bereken de stroomsterkte Ip in de primaire spoel. Ga er daarbij van uit
dat de transformator in de variac een ideale transformator is.
d Meting van de primaire stroomsterkte levert in deze situatie een ander
resultaat: Ip = 0,109 A. Is de transformator in de variac een ideale
transformator? Leg uit waarom wel of niet.
e Voor het bepalen van het rendement van de variac is het primaire
vermogen Pp en het secundaire vermogen PS gemeten bij een aantal
waarden van de secundaire spanning over de lamp. De meetresultaten
zijn weergegeven in het diagram van figuur 32.
Teken in figuur 32 het verband tussen Pp en Ps als de transformator in de
variac een ideale transformator zou zijn.
f
Bepaal met behulp van het diagram van figuur 32 bij welk primair
vermogen Pp het rendement  van de variac 0,80 (of 80%) is.
42
40 Vermogensverlies in de bovenleiding
Hogere spanning bespaart NS energie
De Nederlandse Spoorwegen willen de
spanning op de bovenleiding aanzienlijk
verhogen, tot 25.000 volt. De huidige
spanning van 1.500 volt voldoet steeds
minder naarmate het op het
Nederlandse spoor drukker wordt.
Een optrekkende trein trekt een stroom
van vijfduizend ampère uit de
bovenleiding. Als twee treinen dicht op
elkaar rijden, is de stroom door de
bovenleiding zo groot dat de spanning
aanzienlijk kan dalen, waardoor treinen
minder snel kunnen optrekken en de
dienstregeling soms minuten wordt
vertraagd. Soms moet de ene machinist
terugschakelen om de andere de
gelegenheid te geven om op snelheid te
komen.
Een hogesnelheidstrein kan met 1.500
volt al helemaal niet uit de voeten. Op
topsnelheid zou zo'n trein tienduizend
ampère uit de bovenleiding moeten
trekken, en dat lukt niet. De oplossing
waarvoor de NS nu hebben gekozen, is
overschakelen op 25.000 volt. Bij die
spanning heeft een trein niet meer dan
een paar honderd ampère nodig.
Door de veel geringere stroomsterkte
kan de spanning op de bovenleiding
veel beter worden beheerst. Het aantal
onderstations (plaatsen waar de
bovenleiding wordt gevoed) zou zelfs
van 150 tot 38 kunnen worden
teruggebracht.
Doordat de energieverliezen in de
bovenleiding afnemen, verwachten de
NS tien tot twintig procent op de
energierekening te kunnen besparen.
De warmteontwikkeling in de
bovenleiding is nu aanzienlijk: op
plaatsen waar om de acht minuten een
trein passeert, loopt de temperatuur
soms op tot dertig graden.
De NS willen de nieuwe spanning heel
geleidelijk invoeren. Allereerst zijn de
nieuwe hogesnelheidslijnen en de
Betuweroute aan de beurt. Daarna
zullen in de loop der jaren ook andere
routes worden omgezet.
Bron: Intermediair, 1994.
In het artikel is sprake van optrekkende en rijdende treinen. Die krijgen het
benodigde elektrisch vermogen toegevoerd vanuit de bovenleiding: een
dubbele koperen kabel met een gezamenlijk dwarsdoorsnedeoppervlak van
2,3 cm². Aan deze bovenleiding wordt elektrisch vermogen toegevoerd in een
onderstation. De bovenleiding moet dus een elektrisch vermogen
transporteren van het onderstation naar de trein.
a Hoe groot is het elektrisch vermogen dat een optrekkende trein volgens
het artikel nodig heeft? Leg uit waarom het niet altijd meer lukt om dit
vermogen bij de lage spanning op te nemen.
b Bereken de stroomsterkte die de optrekkende trein uit het artikel nodig
heeft bij de nieuwe, hogere spanning. Leg uit welk gevolg dit heeft voor
het vermogensverlies in de bovenleiding.
c Een optrekkende trein bevindt zich op een afstand van 1,0 km van een
onderstation. Het onderstation zet de huidige spanning van 1500 V op de
bovenleiding. Bereken het rendement van het vermogenstransport.
Gebruik daarbij de in het artikel genoemde stroomsterkte die `een
optrekkende trein uit de bovenleiding trekt'.
43
d Bereken het rendement van het vermogenstransport in dezelfde situatie
(optrekkende trein op 1,0 km afstand van het onderstation), maar nu bij
de nieuwe, hogere spanning op de bovenleiding.
e Komt het verschil in rendement bij opdracht 56c en d overeen met de
besparing die de NS verwacht?
f
41
Leg uit waarom er bij het overschakelen op een hogere spanning minder
onderstations nodig zijn.
Inductielus
Lees eerst het onderstaande krantenartikel:
Onzichtbare lussen in het wegdek meten snelheid voertuigen
Met onzichtbare lussen in het wegdek
meet Rijkswaterstaat sinds juni op
Rijksweg 13 (tussen Den Haag en
Rotterdam) overtredingen van de
maximumsnelheid. De lussen zijn
verbonden met een meetstation dat
voorzien is van een digitale
videocamera. Op die manier kunnen de
snelheidsovertreders permanent worden
geregistreerd op kenteken. De
apparatuur is eigenlijk bedoeld om de
kennis over verkeersstromen te
vergroten. Door de lussenelektronica
(twee magnetische velden die reageren
op ijzer en die impuls doorgeven aan het
meetstation) weet de Dienst
Verkeerskunde hoeveel voertuigen er
over de weg gaan en op welk tijdstip de
file begint. Op dat moment gaan de
borden aan die de adviessnelheid aan
de weggebruikers doorgeven. Maar het
nieuwe systeem is dus ook uiterst
bruikbaar om de pakkans op
snelheidsovertredingen te vergroten.
Bron: de Volkskrant, 1990.
Voor snelheidsmetingen zijn twee lussen op enige afstand van elkaar in het
wegdek aangebracht. Elke lus bestaat uit enkele koperen windingen van zo'n
1,5 bij 2,0 m, aangesloten op een spanningsbron in het meetstation. Door de
windingen van een lus loopt dus continu stroom. Het verschijnen en weer
verdwijnen van een stuk ijzer (een voertuig) boven een lus veroorzaakt een
verandering van de stroomsterkte. Dit signaal wordt in het meetstation
gedetecteerd.
 Hoe ontstaat dit signaal, hoe ziet het er uit en hoe is daarmee de snelheid
van het voertuig te bepalen?
44
42
Lastransformator
Een lastransformator heeft een secundaire spoel met 5 windingen, een
primaire spoel met 190 windingen en een rendement van 0,90 (of 90%). De
transformator is aangesloten op de netspanning van 230 V. De elektrische
installatie is beveiligd met een 16 A zekering. De twee elektroden van de
lastransformator hebben beide een oppervlakte A van 5,0 mm² en een
weerstand Re van 7,5 m. Tussen de twee elektroden zitten bij het lassen
twee staalplaten met elk een dikte d van 1,5 mm.
 Smelt de 16 A zekering in de elektrische installatie wel of niet door?
a Laat met een berekening zien dat de weerstand van de staalplaten tussen
de twee elektroden verwaarloosbaar klein is ten opzichte van de
weerstand van de elektroden zelf.
b Bereken achtereenvolgens het door de transformator geleverde en
opgenomen elektrisch vermogen. Hoe groot is dan de primaire
stroomsterkte?

43
Wat is je conclusie: smelt de zekering wel of niet door?
Dynamo-effect
Een boormachine die bij het boren steeds zwaarder wordt belast, gaat
langzamer draaien. Bij een toenemende belasting neemt het toerental van
een elektromotor dus af. Daarbij blijkt de stroomsterkte toe te nemen. De
stroomsterkte is maximaal als de motor zo zwaar wordt belast dat hij
blokkeert. In dat geval is er een grote kans op doorbranden van de motor als
gevolg van de warmteontwikkeling in de rotorspoel. Het verband tussen de
stroomsterkte I en het toerental n wordt gegeven door het diagram van
figuur 45.
De elektromotor is een draaispoelmotor: een rotorspoel in het magnetisch
veld van de stator. Als er een stroom door de rotorspoel loopt, zorgen de
lorentzkrachten ervoor dat de rotorspoel draait. Maar dan is er sprake van
een draaiende spoel in een magnetisch veld. En dus ontstaat er een
inductiestroom in de spoel en een inductiespanning over de spoel. Dit
noemen we het dynamo-effect bij een elektromotor.

Hoe is met dit dynamo-effect het verband tussen de stroomsterkte en het
toerental bij een elektromotor te verklaren?
a Bepaal de richting waarin de rotorspoel in de draaispoelmotor van figuur
46 vanuit de getekende beginstand gaat draaien. Verklaar het ontstaan
van een inductiestroom in de rotorspoel. Bepaal de richting van deze
inductiestroom en het teken van de inductiespanning. Welk effect heeft
deze inductiespanning op de stroomsterkte?
b Leg uit hoe de inductiespanning afhangt van het toerental van de
rotorspoel. Wat is je conclusie: hoe is het verband tussen de
stroomsterkte en het toerental bij een elektromotor te verklaren?
45
44
Waterkrachtcentrale
Bij een waterkrachtcentrale is de dynamo (of: generator) gekoppeld aan een
waterturbine. Deze turbine wordt aangedreven door het vallende water. De
energie Ein die het vallende water levert aan de turbine is te berekenen met
de volgende formule: Ein= m∙g∙h.
In deze formule is Ein de door de waterturbine opgenomen energie (in j), m
de massa (in kg) van het vallende water en h de valhoogte (in m) van het
water. De waarde van de constante g in deze formule is 9,81 N/kg.
Bij de waterkrachtcentrale in de Rijn bij Maurik stroomt per seconde 400 m³
water door de turbines. Het hoogteverschil van het water voor en achter de
centrale is 3,0 m. De centrale levert dan een elektrisch vermogen van 10
MW.

Hoe groot is het rendement van deze waterkrachtcentrale?
46
Examenopgaven
Opgave 2 Fietsdynamo (2007-2)
2p
4
Met een fietsdynamo kunnen we de lampjes van een fiets laten branden.
Leg uit hoe met een dynamo spanning wordt opgewekt. Gebruik daarbij in
ieder geval het woord flux.
Berend onderzoekt de spanning van een bepaald type fietsdynamo. Bij dit
type draait de magneet rond tussen repen weekijzer die de uiteinden van de
weekijzeren kern van de spoel vormen. Zie figuur 4.
De magneet blijkt aan de buitenkant acht polen te hebben: om en om een
noord- en een zuidpool. De tekening van figuur 5 toont een bovenaanzicht
van de magneet en de repen weekijzer. De grijs gekleurde repen W1 vormen
dus samen het ene uiteinde van de weekijzeren kern en de wit gekleurde
repen W2 samen het andere uiteinde.
Op deze dynamo sluit hij een lampje aan. Vervolgens brengt hij het wieltje
van de dynamo aan het draaien. Hij maakt een diagram van de spanning over
het lampje tegen de tijd. Zie figuur 6.
3p
4p
5
6
Bepaal de frequentie waarmee het wieltje ronddraait.
Om het rendement van de dynamo te bepalen bouwt Berend de opstelling van
figuur 7. De elektrische schakeling die bij deze opstelling hoort, is getekend
in figuur 8.
Als hij het gewichtje loslaat, gaat het wieltje van de dynamo draaien. Enige
tijd na het loslaten bereikt het gewichtje een constante snelheid. Na het
bereiken van de constante snelheid legt het gewichtje in 1,3 s een afstand van
1,00 m af.
De massa van het gewichtje is 200 g. De effectieve waarde van de geleverde
wisselspanning is 1,6 V. De grootte van de weerstand is 8,0 Ω.
Bereken het rendement van deze dynamo voor de omzetting van
zwaarte-energie in elektrische energie in deze situatie.
Opgave l Ding-dong (2006-2)
3p
1
In figuur l zie je een foto van de binnenkant van een bepaald type
huisdeurbel: de ding-dong. Figuur 2 is een schematische tekening
daarvan.
In figuur 2 is de ding-dong aangesloten op een gelijkspanningsbron. S is
de drukknop van de huisbel. Als je schakelaar S indrukt, ontstaat er een
magneetveld in de spoel en gaat de ijzeren pen in de spoel omhoog. Bij A
botst hij tegen de rechterklankstaaf. Je hoort: 'ding'. Na het loslaten van S
valt de pen weer omlaag en botst bij B tegen de linkerklankstaaf. Je
hoort: 'dong'. Een veer zorgt ervoor dat de ijzeren pen weer terugkomt in
de beginpositie.
Leg uit of de 'ding-dong' ook kan werken bij gebruik van een
wisselspanningsbron.
Opgave l Steppen (2006-1)
Arie en Bianca wijden hun praktische opdracht aan natuurkundige aspecten van het steppen.
In figuur l zie je een foto van de step die zij gebruiken.
Zij willen de snelheid van de step gaan meten. Daarom bevestigen zij tussen twee spaken van het
voorwiel een kleine magneet en op de voorvork een spoel. Zie figuur 2.
Als ze de spoel op een oscilloscoop aansluiten en het wiel laten draaien, zien ze het
oscilloscoopbeeld van figuur 3.
3p
3p
1
Telkens wanneer de magneet de spoel passeert, vertoont het oscilloscoopbeeld eerst een piek
omlaag direct gevolgd door een piek omhoog.
Leg dit uit.
2
De tijdbasis van de oscilloscoop staat ingesteld op 50 ms per schaaldeel.
De wielen van de step hebben een diameter van 37,5 cm.
Bepaal de snelheid van de step die hoort bij het oscilloscoopbeeld van figuur 3.
48
Opgave 4 Magneten (2005 – 2)
3p
14 
3p
15 
In de foto van figuur 10 zie je twee identieke, ringvormige magneten om
een houten stok. De bovenste magneet zweeft doordat de noordpolen van
de magneten naar elkaar toe zijn gericht.
→
Teken zowel in R als in S de vector B die de richting van het resulterende
magneetveld van de twee magneten weergeeft.
De magneten hebben gelijke massa.
Teken in de figuur alle krachten die op de onderste magneet werken in de
juiste verhouding. Je hoeft daarbij niet te letten op het aangrijpingspunt
van de krachten.
Boven de magneten zit een spoel om de houten stok geklemd. Zie figuur 11.
De spanning die deze spoel afgeeft, wordt gemeten.
2p
16 
De bovenste magneet wordt naar beneden geduwd en daarna losgelaten. De magneet voert vervolgens een
gedempte trilling uit. In de spoel ontstaat daardoor een wisselspanning.
In figuur 12 is deze wisselspanning als functie van de tijd weergegeven.
De meting is niet direct bij het loslaten van de magneet gestart.
Leg uit of de magneet zich in een uiterste stand of in de evenwichtsstand bevindt op het moment dat de
spanning een maximum vertoont.
Opgave 3 Trafo-koken (2008 – 1)
3p 10
3p 11
5p 12
Bij een demonstratieproef in de klas wordt een transformator
gebruikt. Zie foto. Het rechthoekige juk is de weekijzeren
kern. De primaire spoel van de transformator heeft 600
windingen. De secundaire spoel bestaat uit een aluminium ring
in de vorm van een goot. Deze goot kan een vloeistof bevatten.
De transformator wordt aangesloten op een wisselspanning.
Leg uit hoe de transformator ervoor zorgt dat er een stroom
gaat lopen door de aluminium ring.
De primaire spoel wordt aangesloten op de netspanning van 230 V. De stroom door deze spoel is dan 4,6 A.
Neem aan dat dit een ideale transformator is.
Bereken de stroomsterkte in de aluminium ring.
De transformator wordt uitgezet en in de gootvormige ring wordt 5,0 g water
gebracht. De temperatuur van het water en de aluminium ring is 25 °C. De
warmtecapaciteit van de aluminium ring is 88 J K−1. Nadat de transformator is
aangezet, stijgt de temperatuur van de ring en het water in 9,0 s tot 100 °C.
Bereken welk percentage van de in die 9,0 s toegevoerde elektrische energie
nodig is voor het verwarmen van de ring met water
49
Opgave 5 Schudlamp (2008 – 1)
Een schudlamp is een lamp die licht kan geven nadat je hem hebt heen en weer geschud. Zie figuur.
2p 18
3p 19
In het handvat zit een vaste spoel. Bij het schudden gaat een magneet door deze spoel heen en weer.
Hierdoor wordt in de spoel een inductiespanning opgewekt.
Leg uit dat er zowel een positieve als een negatieve spanning ontstaat als de
magneet één keer door de spoel gaat.
Schets het verloop van de inductiespanning als de magneet door de spoel beweegt met constante snelheid.
Geef in dezelfde figuur aan hoe de grafiek verandert als de snelheid gehalveerd wordt.
50
Antwoorden hoofdstuk 9
1
Zelf doen en controleren met behulp van ijzervijlsel.
2
Het veld in de spoel loopt naar rechts. De magnetische
domeinen in het staal worden naar rechts gericht,
rechts ontstaat de N-pool.
3
De linkerspoel heeft rechts een Z-pool, de rechterspoel
aan de linkerkant ook: afstoting.
4
B = μ0 . N . I / ℓ
1,4.104
5
Elektromagneet in relais, deurbel, opnamekop van de
cassetterecorder, idem van videorecorder,
transformator, enzovoort.
Men gebruikt een elektromagneet als de magneet via
een elektrische stroom in- en uitgeschakeld moet
kunnen worden, of als de sterkte regelbaar moet zijn.
Bij de luidspreker zie je een toepassing van een
permanente en een elektromagneet.
R.h.r: naar rechts.
7
R.h.r: naar links.
8
De formule is FL = B.I.ℓ , alleen factoren die in de
formule voorkomen hebben invloed. Verder moet de B
loodrecht op de I staan.
De lengte AB heeft geen invloed, buiten het veld werkt
geen kracht. De breedte b heeft ook geen invloed.
De lengte ℓ en F zijn recht evenredig, zie de formule.
B en F zijn recht evenredig.
I en F zijn recht evenredig.
De afstand van AB tot de N-pool heeft geen invloed,
de B is in elk punt even groot (homogeen veld). De
breedte b en de lengte AB hebben ook geen invloed.
9
a. De stroomrichting is FE (r.h.r : B omlaag en F naar
rechts).
b. FL = B . I . ℓ = 0,92 . 0,58 . 0,24 = 0,13 N.
10
Luidspreker
a. De omtrek van de cirkel is π . d = 3,14 . 1,2 = 3,77
cm. N = ℓ / (π . d) = 40 / 0,0377 = 1,1.103.
b. De kracht is in alle punten naar links (linkerfiguur)
en naar voren (rechterfiguur).
c. FL = B . I . (N.ℓ) = 0,190 . 0,23 . 40 = 1,748 = 1,7 N.
d. x = F / C = 1,75 / 1,6.103 = 1,1.10-3 m = 1,1 mm.
12
Faraday-pomp
a. De stroom gaat van links naar rechts door het
natrium.
b. De stroom is naar rechts, het magneetveld is
omhoog en volgens de r.h.r is de kracht dan naar
voren gericht.
c. FL = B . I . ℓ = 0,78 . 90 . 0,022 = 1,5 N.
14
Rechterhandregel: van boven naar beneden.
N / ℓ = 24.10-3 / (1,26.10-6 . 1,4) =
6
11
13
a. BS = μ0 . N . I / ℓ =>
BS = 1,26.10-6 .3000. 2,2 /
0,15 = 5,54.10-2 T naar links in de spoel.
b. Op de onderkant is FL naar onderen, op de voorkant
is FL naar voren, op de bovenkant is FL naar boven, op
de achterkant is FL naar achteren.
Op elke zijde is FL = B . I . ℓ = 5,54.10-2 . 0,050 . 0,015
= 4,2.10-5 N.
c. Alle krachten zijn recht naar buiten gericht, dwars op
de richting waarin de spoel zou kunnen bewegen.
Q
P
15
a. Zie de figuur hiernaast.
b. Punt P ligt recht onder de draad, op 3,2 mm
s=afstand.
c. Nu is er verdubbeling omdat de velden elkaar
versterken: BQ = 5,0 mT.
16
Zie de figuren hieronder.
a
B c
b
F
B
I
I
B
I
geen F
geen F
17
Motormoment
a. Een grotere l geeft een grotere kracht, een grotere
b geeft een grotere arm tot het draaipunt. Beiden
zorgen voor een ‘sterkere’ motor.
b Een dunne koperdraad heeft een hoge weerstand
en daardoor wordt de stroomsterkte kleiner.
c. R = ρ·ℓ / A = 17·10-9 ×600×0,12 / 0,15.10-6 = 8,16 Ω
=> I = 6,0 / 8,16 = 0,74 A.
d FL = N . B . I . ℓ = 600 . 0,085 . 0,74 . 0,035 = 1,3 N
18
Lanceerinrichting
FL = B . I . ℓ = 2,5 . 1,7.106 . 0,020 = 85.103 N = 85 kN.
Dat is in overeenstemming.
F . Δt = m . Δv
=>
Δv = veind = 85.103 .
2,0.10-3 / 0,080 = 2,1.103 m/s = 2,1 km/s.
19
Zonne-auto
Het zonnepaneel zet stralingsenergie om in elektrische
energie en warmte.
Het omgezette stralingsvermogen is 8,0 kW.
De motor zet elektrische energie om in
bewegingsenergie en warmte.
70 km/h = 19,4 m/s.
Het geleverde mechanisch vermogen is P = F . v = 50 .
19,4 = 970 W.
η = 0,970 / 8,0 = 0,12 of 12%.
a. R.h.r.: AB draait naar achteren, DC naar voren.
b. FL (0) = N . B . I . ℓ . = 50 . 0,48 . 0,128 . 0,085 =
0,26 N.
c. Na 90 draaiing is het moment nul en komt het
draadraam tot rust.
d. In de eindstand is de kracht op AD en BC nog
steeds 0,26 Nl.
51
Antwoorden hoofdstuk 10
29 a.
20 a. De magneet bewegen.
b. Er ontstaat een wisselspanning.
c. Het geluid zet een plaatje in trilling. Daaraan zit
een klein spoeltje dat vlak bij een magneet heen en
weer trilt. Daardoor ontstaat wisselspanning.
b. Er werkt alleen een lorentzkracht op het deel
van de spoel dat binnen het magneetveld zit. In
beide gevallen is de nettokracht naar links.
c. De Lorentzkracht werkt de beweging tegen
(ook volgens de wet van Lenz)
21 a. geen magneetveld, geen spanning,
b. veranderend magneetveld, dus spanning.
c. constante magneetveld, geen spanning.
d. veranderend magneetveld, dus spanning.
22 a. De elektromagneet levert een wisselend
magneetveld.
b. De flux blijft voortdurend veranderen van
richting, de spanning en de stroom dus ook.
c. Ja, het magneetveld wordt sterker.
d. Ja, het veld verandert sneller.
30 Fietsdynamo
a. Het magneetveld staat dan dwars op de spoel, de
flux is nul.
b Bij de eerste top (t=1,6)
c De flux (naar rechts) neemt toe. De spoel maakt
een tegenveld naar links, de stroom gaat van links
naar rechts door de spoel.
d De flux daalt, de spoel maakt dus een
magneetveld naar rechts, dan loopt de stroom de
andere kant op.
e Als de flux het meest verandert, de helling is dan
maximaal: in de punten waar de flux nul is.
f
23 a. Registreren of er een auto staat of overheen rijdt,
b. Als er een auto rijdt.
c. Het metaal van de auto wordt magnetisch door
de stroom in de lus.
24 Van 0-4 s: ΔΦ = 8,0.10-2 Wb; Δt = 4,0 s, N = 150.
Uind = 150 × 8,0.10-2 / 4,0 = 3,0 V. (negatief
getekend omdat de flux groeit, wet van Lenz)
Van 4-6 s: ΔΦ = -8,0.10-2 Wb; Δt = 2,0 s, N = 150.
Uind = 150 . -8,0.10-2 / 2,0 = 6,0 V.
Uind (V)
6
4
2
0
0
2
4
6
t (s)
-2
31
b
c
d
-4
25 Van 0 - 2 s en 4, -> is ΔΦ = 0, dus is Uind = 0 V.
Van 2 - 4 s is ΔΦ = 4,0.10-6 Wb, Δt = 2,0 s en N =
1200.
Uind = 1200 × 4,0.10-6 / 2,0 = 2,4.10-3 V = 2,4 mV.
a W = F . s = 0,65 . 9,8 . 1,0 = 6,37 J,
I = U/R = 5,7/30 = 0,19 A, P = UI = 5,70,19 = 1,08
E = Pt = 1,084,7 = 5,1 J
η = Elamp / W = 5,1 / 6,37 = 0,79
32 Dynamospanning
a. Φ = B∙A = 0,085×0,025×0,035 = 7,4∙10 -5 Wb
b. Δt = halve periode = 0,01 s; ΔΦ = 2×Φmax
U = N∙ΔΦ/Δt = 400×2×7,4.10-5 / 0,01 = 5,9 V
26 Uind is maximaal als ΔΦ / Δt maximaal is, dus als
de r.c. van de raaklijn maximaal is. De afgeleide is
maximaal in het buigpunt: teken de raaklijn bij t =
1,75 s.
Uind = 1 . -3,0.10-6 / 2,5.10-2 = -1,2.10-4 V
= -0,12 mV.
33 Afvalscheiding
a. Alleen ijzer, nikkel en kobalt worden door een
magneet aangetrokken.
b. Een toenemend magneetveld in één winding
veroorzaakt een inductiespanning. Omdat de
stroomkring gesloten is, gaat er een stroom lopen.
Het veld van de spoel is naar rechts, dat van de
ring is naar links: er is afstoting.
c. De snel roterende magneten zorgen voor een snel
wisselend veld. In de aluminium onderdelen
ontstaat een inductiestroom die voor afstoting
zorgt.
27 a. Φmax = 3,0.10-3 . 6,0.10-4 = 1,8.10-6 Wb,
b. De fluxverandering is twee keer de maximale
flux. <Uind> = 100×2× -1,8.10-6 / 0,10 = -3,6.10-3 V .
28 a. De magnetische flux in de linkerspoel neemt toe
en het veld is naar links gericht. Volgens de wet
van Lenz maakt de rechter spoel een veld naar
rechts. R.h.r.: de stroom gaat in de spoel naar
links en door de weerstand naar rechts.
b. De linkerkant van de spoel is de pluspool, de
rechter de minpool. De stroom loopt buiten de
spanningsbron van plus naar min en binnen de
spanningsbron wordt de stroom van min naar plus
‘geduwd’.
34 Dynamorendement
a. Pm = F . s / t = F . v
v=2.π.r/T=2.π.r.n
Pm = 2 . π . r . F . n.
b. s = 2 . π . r . n
rw .nw = rd .nd
0,69 . 2,0 = 0,030 . nd
nd = 46
I = 0,30 + 0,20 = 0,50 A Pe = 6,0 . 0,50 = 3,0 W
Pm = 2 . π . 0,015 . 1,20 . 46 = 5,2 W
=>
η = 3,0 / 5,2 = 0,58
35 Ja, er is een gesloten stroomkring door de
primaire spoel. (De adapter voelt warm aan.)
52
motor van de trein staan. Maar aanvoerkabels en
trafo’s zijn duur. Men zal een optimum zoeken.
36 a. Np : 300 = 230 : 12 =>
Np = 5,8.103.
b. 12 . Is = 20
=>
Is = 1,7 A
230 . Ip = 20
=>
Ip = 8,7.10-2 A.
c. Ja, er moet meer stroom door de windingen. Het
is verstandig om minder windingen, maar in
dezelfde verhouding, te nemen. Ook de diameter
van de draad kan groter zijn.
41 Inductielus
I
37 Us .Is / (Up .Ip ) = 12,1×0,52 / (229×0,0289) = 0,95
38 a. Np : Ns = Up : Us
4400 : 260 = 230 : Us
Us = 13,6 V.
b. Us . Is = 0,80 . 18 = 14,4 W.
Is = 14,4 / 13,6 = 1,1 A.
t
Een stroom door een spoel (lus) maakt een
magneetveld. Het ijzer van een auto boven de lus
versterkt het magneetveld. Daardoor neemt de
magnetische flux in de spoel toe en ontstaat er een
inductiespanning. De stroom die door deze
inductiespanning wordt opgewekt zal tegenwerken, de
stroomsterkte neemt af. Als de auto de lus verlaat,
gebeurt het omgekeerde.
De lengte van de auto bepaalt mede de afstand tussen
de twee signalen. Met twee lussen op een bekende
onderlinge afstand en de tijdsduur tussen
overeenkomstige pieken of dalen is de snelheid van de
auto te bepalen.
39 Variac
a. Omhoog: er zijn dan meer secundaire windingen
in de kring opgenomen.
b. Bij het maximale aantal is: 220 : 260 = 440 : Ns
=> Ns = 520.
Bij het minimale aantal is: 220 : 6,0 = 440 : Ns
=> Ns = 12.
c. Up . Ip = Us . Is => 220 .Ip = 100 . 0,179
=> Ip = 0,081 A.
d. De transformator is niet ideaal: Pp > Ps .
e. Zie de figuur, de lijn met Pp = Ps.
f. Zie in de figuur de stippellijn met Ps = 0,80. Pp en
het snijpunt met de originele lijn. Pp = 31 W.
42 Lastransformator
a. R = ρ . ℓ / A = 0,72.10-6 . 3,0.10-3 / 5,0.10-6 =
4,3.10-4 Ω = 0,4 mΩ.
Dit is te verwaarlozen ten opzichte van 15 mΩ.
b. Us = 230 . 5 / 190 = 6,05 V.
Is = 6,05 / 0,0154 = 393 A.
Ps = 6,05 . 393 = 2377 W.
Pp = 2377 . (100 / 90) = 2641 W
Ip = 2641 / 230 = 11,5 A.
De zekering brandt niet door.
43 Dynamo-effect
a. Door de rechterkant van de winding gaat I naar
achteren en is B naar rechts gericht. De Lorentzkracht is omlaag. De winding gaat in de richting
van de wijzers van de klok draaien. (Rechtsom of
(wiskundig) negatief.)
Een winding die in een magneetveld draait, werkt
als een dynamo die een (tegenwerkende)
inductiestroom opwekt. Deze inductiestroom loopt
van de linkerkoolborstel door de winding naar de
rechter. Het dynamo-effect levert in de
rechterkoolborstel een plus- en in de linker- een
minpool. Deze spanningsbron werkt de uitwendige
tegen, de stroomsterkte in de motor wordt kleiner.
b. Naarmate het toerental toeneemt, neemt ook de
inductiespanning toe. De tegenwerkende
inductiestroom neemt toe waardoor de totale
stroom door de motor afneemt.
40 Vermogensverlies in de bovenleiding
a. P = U . I = 1500 . 5000 = 7,5.106 W. Bij een lage
spanning is de stroomsterkte zeer groot en
daarmee het spanningsverlies over toe- en
afvoerleidingen, want Pverlies = I2 . R.
b. I = P / U = 7,5.106 / 25.000 = 300 A..
Pverlies = I2 . R is nu veel kleiner.
c. R = ρ . ℓ / A = 17.10-9 . 1,0.103 / 2,3.10-4
= 7,4.10-2 Ω,
U = 5000 . 7,4.10-2 = 370 V.
Pverlies = U . I = 370 . 5000 = 1,85.106 W.
η = (7,5.106 - 1,85.106 ) / 7,5.106 = 0,75 (75%).
d. I = 300 A (zie b.); R = 7,4.10-2 Ω (zie c.)
U = 300 . 7,4.10-2 = 22 V,
Pverlies = 22 . 300 = 6,7.103 W.
η = (7,5.106 - 6,7.103 ) / 7,5.106 = 1,00 (100 %).
e. Het rendement gaat van 75 naar 100%, op 1,0 km
afstand is de besparing 25% en dichterbij is dat
minder. Dit geldt voor het optrekken, bij constante
snelheid is de stroomsterkte I kleiner. De
besparing zal dus gemiddeld kleiner zijn en kan
heel goed op de 10 tot 20 % van de NS uitkomen.
f. Minder onderstations maken de Uverlies groter (ℓ is
groter dus R is groter). Maar toch is het
spanningsverlies per km in de kabels kleiner en
daarom blijft er een grotere spanning over de
44 Waterkrachtcentrale
Pin = Ein / t = 400 . 998 . 9,81 . 3,0 / 1,00 = 11,7.106 W.
η = Pelek / Pin = (10 / 11,7) . 100 % = 85 %.
53