Rakende grafieken.

Rakende grafieken.
1.
Examenvraagstuk VWO Wiskunde B, 2010
Voor n = 1, 2, 3, ... is de functie f n gegeven door f n ( x)  n  6 x  n
Verder is gegeven de lijn k met vergelijking y = x + 9
Bewijs dat voor elke waarde van n de grafiek van fn de lijn k raakt in het punt met xcoördinaat n + 9.
2.
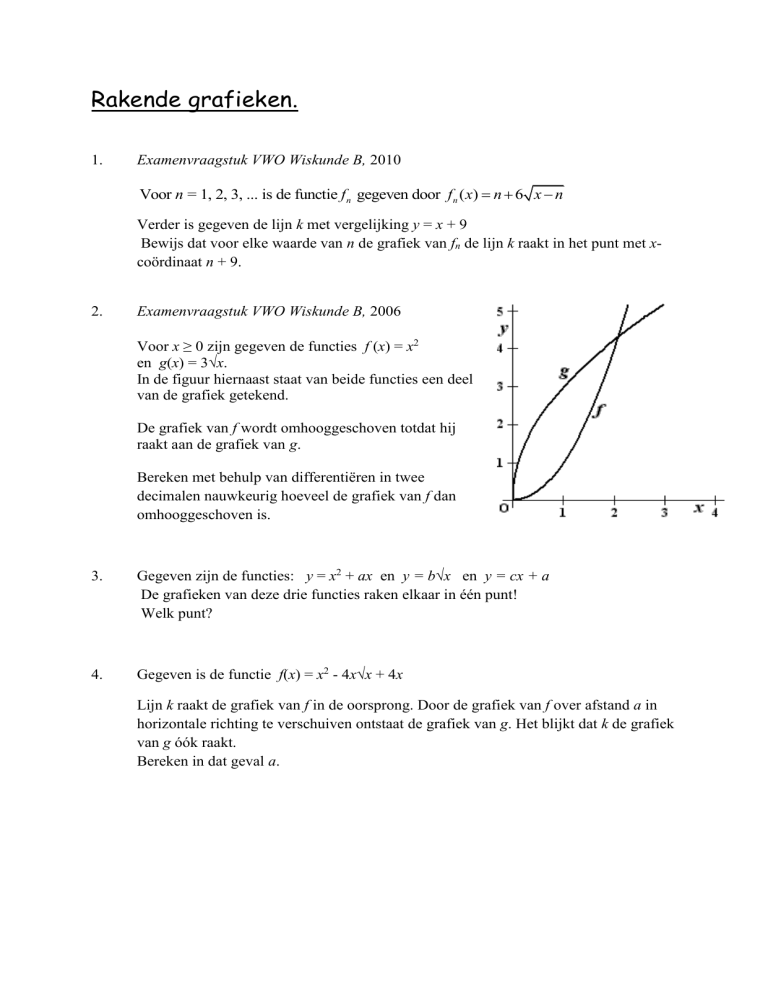
Examenvraagstuk VWO Wiskunde B, 2006
Voor x ≥ 0 zijn gegeven de functies f (x) = x2
en g(x) = 3√x.
In de figuur hiernaast staat van beide functies een deel
van de grafiek getekend.
De grafiek van f wordt omhooggeschoven totdat hij
raakt aan de grafiek van g.
Bereken met behulp van differentiëren in twee
decimalen nauwkeurig hoeveel de grafiek van f dan
omhooggeschoven is.
3.
Gegeven zijn de functies: y = x2 + ax en y = b√x en y = cx + a
De grafieken van deze drie functies raken elkaar in één punt!
Welk punt?
4.
Gegeven is de functie f(x) = x2 - 4x√x + 4x
Lijn k raakt de grafiek van f in de oorsprong. Door de grafiek van f over afstand a in
horizontale richting te verschuiven ontstaat de grafiek van g. Het blijkt dat k de grafiek
van g óók raakt.
Bereken in dat geval a.
1.
x = n + 9 geeft y = n + 6√(n + 9 - n) = n + 6 • √9 = n + 6 • 3 = n + 18 = x + 9
Dus het punt (n + 9, n + 18) ligt inderdaad op beide grafieken.
De helling van y = x + 9 is gelijk aan 1.
De helling van y = n + 6√(x - n) is de afgeleide: y' = 6 • 0,5 • (x - n)-0,5
x = n + 9 geeft dan y' = 6 • 0,5 • (n + 9 - n)-0,5 = 3 • 9-0,5 = 3 • 1/3 = 1
De grafieken hebben in het punt (n + 9, n + 18) beiden helling 1, dus raken ze elkaar
daar.
2.
De functies raken elkaar als f ' = g '
2x = 0,5 • 3 • x-0,5 ⇒ x1,5 = 0,75 ⇒ x = 0,752/3 ≈ 0,83
f(0,83) = 0,6814 en g(0,83) = 2,7256 dus de grafiek van f moet 2,04
omhooggeschoven worden.
3.
x2 + ax = cx + a
x2 + ax = b√x
2x + a = c
c = b/(2√x)
....(1)
....(2)
....(3)
....(4)
(3) invullen in (1), (2), en (4):
x2 + ax = 2x2 + ax + a ⇒ a = -x2 ....(5)
x2 + ax = b√x
....(6)
2x + a = b/(2√x) ....(7)
(5) invullen in (6) en (7):
x2 - x3 = b√x
2x - x2 = b/2√x ⇒ 4x√x - 2x2√x = b
Vul de laatste in in de bovenste:
x2 - x3 = (4x√x - 2x2√x) • √x ⇒ x2 - x3 = 4x2 - 2x3
0 = 3x2 - x3 ⇒ 0 = x2(3 - x) ⇒ x = 0 ∨ x = 3
de laatste geeft het raakpunt (3, -18)
(dat geeft a = -9 en c = -3 en b = -6√3)
4.
f(x) = x2 - 4x√x + 4x
f ' = 2x - 1,5 • 4 • x0,5 + 4 ⇒ f '(0) = 4
lijn k heeft dus helling 4, en is de lijn y = 4x
waar heeft de grafiek van f nog meer helling 4?
2x - 1,5 • 4 • x0,5 + 4 = 4
2x - 6√x = 0 ⇒ 2√x(√x - 3) = 0 ⇒ √x = 0 ∨ √x = 3 ⇒ x = 0 ∨ x = 3
x = 3 geeft y = 32 - 4 • 3√3 + 4 • 3 = 21 - 12√3
waar heeft k die y-coördinaat?
y = 21 - 12√3 = 4x ⇒ x = 5,25 - 3√3
de grafiek van f moet dus van x = 3 naar x = 5,25 - 3√3 geschoven worden.
dat is 3 - (5,25 - 3√3) = 3√3 - 2,25 naar links.