Gegevens invoeren - Clzvaklokalen.nl

Uitwerkingen opgaven hoofdstuk 7
7.1
Opgave 1
Opgave 2
Beeldvorming en beeldconstructie
Het beeld van een dia bij een diaprojector wordt gevormd door een bolle lens.
De voorwerpsafstand is groter dan de brandpuntsafstand. Je krijgt dan een
omgekeerd reëel beeld. Het beeld is zowel in horizontale als verticale richting
omgekeerd; links wordt rechts en boven komt onder. Voor een letter p op het
scherm moet de dia als een letter d in de diaprojector worden gedaan.
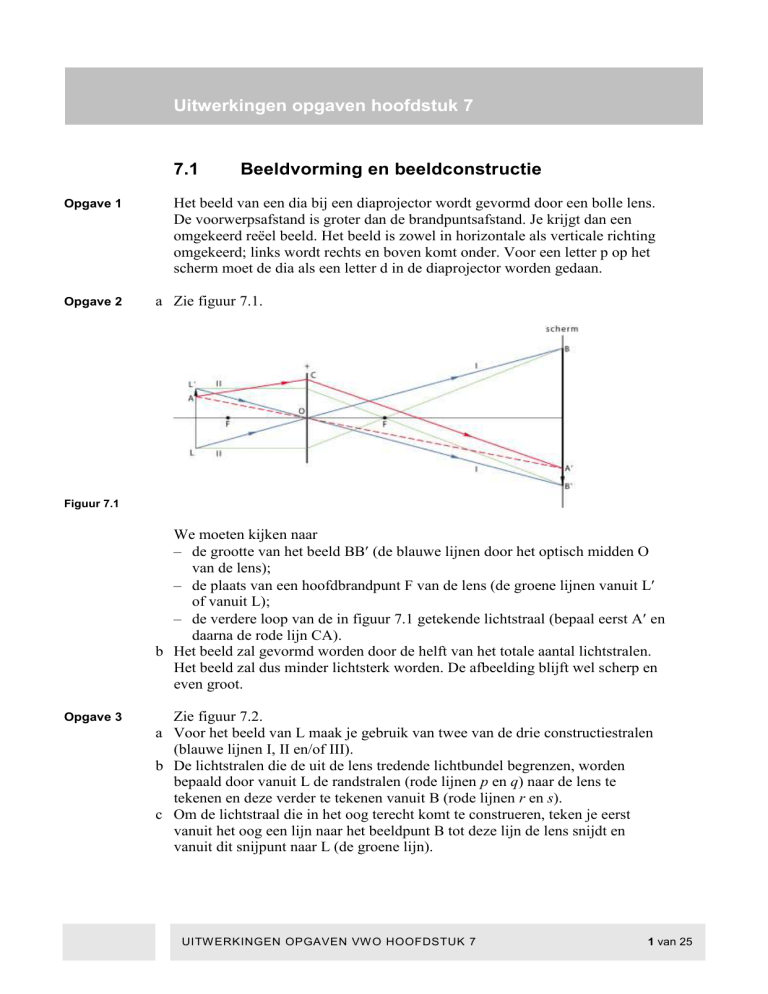
a Zie figuur 7.1.
Figuur 7.1
We moeten kijken naar
– de grootte van het beeld BB (de blauwe lijnen door het optisch midden O
van de lens);
– de plaats van een hoofdbrandpunt F van de lens (de groene lijnen vanuit L
of vanuit L);
– de verdere loop van de in figuur 7.1 getekende lichtstraal (bepaal eerst A en
daarna de rode lijn CA).
b Het beeld zal gevormd worden door de helft van het totale aantal lichtstralen.
Het beeld zal dus minder lichtsterk worden. De afbeelding blijft wel scherp en
even groot.
Opgave 3
Zie figuur 7.2.
a Voor het beeld van L maak je gebruik van twee van de drie constructiestralen
(blauwe lijnen I, II en/of III).
b De lichtstralen die de uit de lens tredende lichtbundel begrenzen, worden
bepaald door vanuit L de randstralen (rode lijnen p en q) naar de lens te
tekenen en deze verder te tekenen vanuit B (rode lijnen r en s).
c Om de lichtstraal die in het oog terecht komt te construeren, teken je eerst
vanuit het oog een lijn naar het beeldpunt B tot deze lijn de lens snijdt en
vanuit dit snijpunt naar L (de groene lijn).
UITW ERKINGEN OPGAVEN VW O HOOFDSTUK 7
1 van 25
Figuur 7.2
Opgave 4
Zie figuur 7.3.
Figuur 7.3
a Voor het tekenen van het virtuele beeld maak je gebruik van de
constructiestralen voor negatieve lenzen (de groene lijnen).
b Trek de lichtstraal door tot aan de lens. Teken een lijn vanuit punt B door het
punt waar deze lichtstraal de lens snijdt (de rode lijnen).
Opgave 5
a Ga ervan uit dat het scherm op beeldafstand van de lens staat. Als er geen
diafragma zou zijn, zou op het scherm een volledige en scherpe afbeelding
zichtbaar zijn. Elk punt van LL is op te vatten als voorwerpspunt. Alle stralen
uit zo’n voorwerpspunt die op de lens vallen, werken mee om een bijbehorend
beeldpunt te maken. Als er een diafragma achter de lens staat, zullen van alle
voorwerpspunten slechts die stralen aan de beeldvorming meewerken die door
het diafragma gaan. Van alle voorwerpspunten gaan er wel stralen na breking
door het diafragma, dus van alle voorwerpspunten ontstaat een beeldpunt. Het
antwoord is dus ja, het beeld is dus volledig.
UITW ERKINGEN OPGAVEN VW O HOOFDSTUK 7
2 van 25
b Nee, het beeld zal minder lichtsterk zijn. Per voorwerpspunt zal nu, vergeleken
met de situatie zonder diafragma, slechts een deel van de lichtstralen
meewerken aan de vorming van een beeldpunt.
c Het beeld is nog steeds scherp, omdat het scherm op beeldafstand van de lens
staat. Elk voorwerpspunt wordt op deze beeldafstand afgebeeld. Het antwoord
is dus nee, het diafragma houdt alleen een deel van de lichtstralen tegen. Het
beeld wordt dan gevormd door minder lichtstralen dan wanneer er geen
diafragma zou zijn. Het beeld zal dus minder fel zijn, maar wel scherp.
d Voor het construeren van het beeld maak je wederom gebruik van de
constructiestralen. Hierbij negeer je als het ware het diafragma. (De rode lijnen
vanuit L en de groene lijnen vanuit L.) Zie figuur 7.4.
Figuur 7.4
Opgave 6
Zie figuur 7.5.
Figuur 7.5
– De plaats van de (positieve) lens vind je door de lijn BL te tekenen en het
snijpunt te bepalen met de hoofdas (blauwe lijnen).
– De plaats van het linkerhoofdbrandpunt van de lens vind je door vanuit B
een lijn te tekenen evenwijdig aan de hoofdas. Teken vanuit het snijpunt van
deze lijn met de lens een lijn naar L en trek deze door tot hij de hoofdas
snijdt (de groene lijnen).
– De verdere loop van de in figuur 7.5 getekende lichtstraal vind je door eerst
het snijpunt van deze lijn te bepalen met de lens en de lijn dan verder te
tekenen vanuit B (de rode lijnen).
Opgave 7
a Omdat de zon zo ver weg staat, lijken lichtstralen die vanuit één punt komen
evenwijdig op de lens in te vallen. Deze lichtstralen snijden elkaar in het
brandvlak. De afstand van het scherm tot de lens zal dus gelijk moeten zijn aan
de brandpuntsafstand, en deze afstand is 250 cm.
UITW ERKINGEN OPGAVEN VW O HOOFDSTUK 7
3 van 25
b Als je niet weet waar de lens zich bevindt, dan kun je alleen lichtstralen
tekenen die niet worden gebroken door de lens. Dit zijn de lichtstralen door het
optisch midden van de lens. Zie figuur 7.6a.
Figuur 7.6a
De evenwijdige lichtbundel afkomstig van de bovenkant van de zon, zal een
beeldpunt vormen in punt P op het scherm. Teken vanuit dit punt P een lijn (de
rode stippellijn I) die evenwijdig loopt aan de bundel afkomstig van de
bovenkant van de zon. Het snijpunt van deze rode stippellijn met de hoofdas is
het optisch midden O van de lens.
Teken de lens loodrecht op de hoofdas op de plaats van dit snijpunt O.
In plaats van de lichtbundel afkomstig van de bovenkant van de zon, kun je
ook de lichtbundel nemen afkomstig van de onderkant van de zon (de blauwe
lijnen).
c Zie figuur 7.6b.
Figuur 7.6b
De afstand van de zon tot de lens v = 1,50 · 108 km = 1,50 · 1011 m.
v 1,50 1011
 
 6, 0 1010
b
2,50
diameter zonneschijf
v
De verhouding
is even groot als de verhouding
b
diameter lichtvlek
diameter zonneschijf v


d
b
v
 de diameter van de zonneschijf = d   23 · 10–3 × 6,0 · 1010 = 1,4 · 109 m
b
d Als de lens groter is, dan vallen er meer lichtstralen op de lens. Er zullen dus
ook meer lichtstralen de lens verlaten. Het beeld zal dus feller zijn.
UITW ERKINGEN OPGAVEN VW O HOOFDSTUK 7
4 van 25
e De afstand van de lens tot het scherm wordt groter. Uit de gelijkvormigheid
d
van de driehoeken volgt dat de verhouding beeld gelijk is aan de verhouding
b
d zon
.
v
Die verhouding verandert niet. Omdat b groter wordt, wordt de diameter van
het beeld ook groter.
7.2
Lensformule en lineaire vergroting
Opgave 8
a v = 15 cm en b = +60 cm
1 1 1 1 1
5
1
    


f v b 15 60 60 12
 f  12 cm
b 60
N 
 4, 0
v 15
b v = 15 cm en b = –60 cm
1 1 1 1
1
3
1
    


f v b 15 60 60 20
 f  20 cm
b 60 60
N 

 4, 0
v
15
15
c v = 28 cm en f = +20 cm
1 1 1
1 1 1 1
1
1
      


f v b
b f v 20 28 70
 b  70 cm
b 70
N 
 2,5
v 28
d v = 25 cm en N = 3,2×
b
 er zijn twee mogelijkheden: N 
= 3,2×
v
 b1 = +3,2 · v = +80 cm of b2 = –3,2 · v = –80 cm
Mogelijkheid 1 (reëel beeld)
1 1 1 1
1
v = 25 cm en b1 = +80 cm    
  f1  19 cm
f v b 25 80
Mogelijkheid 2 (virtueel beeld)
1 1 1 1
1
v = 25 cm en b2 = –80 cm    

 f 2  36 cm
f v b 25 80
Opgave 9
a Een holle lens heeft een brandpuntsafstand van 20 cm  f = –20 cm.
Eerste situatie
v1 = 60 cm
1 1 1
  
f v1 b1
UITW ERKINGEN OPGAVEN VW O HOOFDSTUK 7
5 van 25

1 1 1
1
1
4
1
  



b1 f v1 20 60
60
15
 b1  15 cm
Tweede situatie
v2 = 12 cm
1 1 1
  
f v2 b2

1 1 1
1
1
  

b2 f v2 20 12
 b2  7,5 cm
b Nee, een holle lens geeft altijd een verkleind virtueel beeld.
Opgave 10
a De dia heeft de afmetingen 40 mm bij 30 mm; het scherm heeft een breedte
van 160 cm en een hoogte van 120 cm
breedte beeld
160 cm
= 40 of
 de vergroting N 

breedte voorwerp 4,0 cm
hoogte beeld
120 cm
 de vergroting N 

 40
hoogte voorwerp 3,0 cm
Omdat een diaprojector een reëel beeld heeft en de vergroting 40× is, geldt:
b = 40 · v.
480
 12 cm.
De afstand tussen projectielens en scherm = b = 480 cm  v 
40
b De beeldafstand, de voorwerpsafstand en de brandpuntsafstand bepalen of een
voorwerp scherp is. Daar wordt niets aan gewijzigd. Ook deze dia zal dus
scherp worden afgebeeld.
c De dia heeft nu de afmetingen 32 mm bij 24 mm; de vergroting N = 40×
 de afmetingen van het beeld zijn (40 × 3,2 cm) bij (40 × 2,4 cm) = 128 cm
bij 96 cm.
De oppervlakte van het scherm: Ascherm = 1,60 m × 1,20 m = 1,92 m2.
De oppervlakte van het beeld: Abeeld = 1,28 m × 0,96 m = 1,23 m2
A
1, 23
 0, 64 (= 64%).
 de verhouding tussen beide oppervlakten is: beeld 
Ascherm 1,92
1 1 1
d De brandpuntsafstand f blijft ongewijzigd.   = constant. De
f v b
1
beeldafstand b wordt groter gemaakt  zal een kleinere waarde aannemen
b
1
 moet dan groter worden om de vergelijking weer kloppend te krijgen. De
v
voorwerpsafstand v zal dan kleiner moeten worden, dus de lens moet iets naar
de dia toegeschoven worden.
e De dia heeft de afmetingen 32 mm bij 24 mm; het scherm heeft een breedte
van 160 cm en een hoogte van 120 cm.
breedte beeld
160 cm
= 50× of
 de vergroting N 

breedte voorwerp 3,2 cm
hoogte beeld
120 cm
= 50×
 de vergroting N 

hoogte voorwerp 2,4 cm
UITW ERKINGEN OPGAVEN VW O HOOFDSTUK 7
6 van 25
Opgave 11
a De dia heeft de afmetingen 36 mm bij 24 mm; het scherm heeft een breedte
van 200 cm en een hoogte van 120 cm 
breedte beeld
200 cm

vergroting N breedte 

 56 
breedte voorwerp 3,6 cm


hoogte beeld
200 cm
vergroting N hoogte 

 50  
hoogte voorwerp 2,4 cm

 maximale vergroting  50 
Omdat een diaprojector een reëel beeld heeft en de vergroting 50× is, geldt:
b = 50 · v.
Eerste manier
1
1 N 1 ( N  1)
1 1 1
   
1 1 1
    
 
b
  f v b  b  b b b
f v b
N
 

b
b 
1 ( N  1)
N  v
 b  f ( N  1)
v
N   
b
f
 b = 0,10 × (50 + 1) = 5,1 m
Tweede manier
Invullen in de lensformule:
1 1 1
 
50
1
51
 1 1 1
 



f v b  
   10 v 50v 50v 50v 50v
b  50v   50v  510  v  10, 2 cm; b  50v  5,1 m
f  10 cm  
b Het diafragma houdt een deel van de lichtstralen tegen, dus het beeld is minder
lichtsterk. Omdat v en f niet veranderen, verandert b niet, en dus verandert N
niet. Er zal niets veranderen aan de plaats, de scherpte en de grootte van het
beeld.
Opgave 12
a Omdat er op een scherm een reëel beeld wordt gevormd en de vergroting 3× is,
geldt: b = 3 · v.
De afstand van het voorwerp tot het scherm s = 80 cm
 s = b + v = 80 cm
  s  3v  v  4v
  4v  80 cm
b  3v


s  b  v  80 cm   v  20 cm;
  b  60 cm
1 1 1 1
1
4
1
   



f v b 20 60 60 15
 f  15 cm
b Omdat er op een scherm een reëel beeld wordt gevormd en de vergroting 5× is,
geldt: b = 5 · v.
UITW ERKINGEN OPGAVEN VW O HOOFDSTUK 7
7 van 25
Eerste manier
1 1 1
  1  1  1  N  1  ( N  1)
 
  f v b b b
b
f v b

1 ( N  1)
b
1 N
 b  f ( N  1)
N     
b
v
v b   f
 b2 = 15 × (5 + 1) = 90 cm
90
 18 cm
 v2 
5
 b2 + v2 = 108 cm
Tweede manier
Invullen in de lensformule:
1
5
1
6
1 1



1 1 1   
 
15 v2 5v2 5v2 5v2 5v2
f v2 b2  
 
   5v2  6 15  90
b2  5v2
  v2  18 cm
  b2  5v2  90 cm
f  15 cm  
 b2  v2  108 cm
Zie figuur 7.7.
Figuur 7.7
Het scherm wordt niet verplaatst.
Het voorwerp stond op 80 cm afstand van het scherm (voorwerp 1) en komt nu
op een afstand van 108 cm van het scherm te staan (voorwerp 2)  het
voorwerp moet 28 cm verplaatst worden van het scherm af (naar links).
De lens stond op 60 cm afstand van het scherm; de lens komt nu op een afstand
van 90 cm van het scherm te staan  de lens moet 30 cm verplaatst worden
van het scherm af (naar links).
UITW ERKINGEN OPGAVEN VW O HOOFDSTUK 7
8 van 25
Opgave 13
a f = 20 cm en v = 30 cm
1 1 1
1 1 1 1
1
1
      
 
 b  60 cm
f v b
b f v 20 30 60
 de beeldafstand b komt niet overeen met de afstand van de lens tot het
scherm
 er ontstaat geen scherp beeld op het scherm, maar een cirkelvormige
lichtvlek.
b Op een afstand van 70 cm. Zie figuur 7.8a.
Figuur 7.8a
c Zie figuur 7.8b.
Figuur 7.8b
v=f
Zie figuur 7.9.
Figuur 7.9
d = 8,0 cm
UITW ERKINGEN OPGAVEN VW O HOOFDSTUK 7
9 van 25
d Omdat v < f ontstaat er een virtueel beeld; v = 15 cm en f = +20 cm.
1 1 1
1 1 1 1 1
1
      
    b  60 cm
f v b
b f v 20 15
60
 er komt een divergerende bundel uit de lens (zie figuur 7.10).
Figuur 7.10
Als het scherm in de richting van de lens wordt geschoven, dan wordt de
lichtvlek kleiner (zie figuur 7.10).
Opgave 14
a Om een maximale stroomsterkte te meten, moet de lichtintensiteit maximaal
zijn. Dat is als er zo veel mogelijk lichtstralen op de LDR vallen. Dat is het
geval als het beeldpunt zich precies op de LDR bevindt.
b Zie figuur 7.11a.
Figuur 7.11a
Figuur 7.11b
Zie figuur 7.11a. v + b = 70 cm.
Zie figuur 7.11b.
Er zijn twee pieken te zien (A en B)  er zijn twee voorwerpsafstanden en dus
ook twee beeldafstanden waarbij een maximum optreedt.
UITW ERKINGEN OPGAVEN VW O HOOFDSTUK 7
10 van 25
Bij piek A:

x  v1  21 cm 
  b1  49 cm 
v1  b1  70 cm 
1 1
1

 f  15 cm
  
f 21 49
1 1 1
 
f v1 b1 
Bij piek B:

x  v2  49 cm 
  b2  21 cm 
v2  b2  70 cm 
1
1
1

  f  15 cm
 
f 49 21
1 1 1 
 
f v2 b2 
c Bij een vaste afstand tussen voorwerp en scherm zijn twee posities mogelijk
waarbij een beeld op het scherm wordt gevormd. Dit kun je zien aan de
lensformule. Als bij een bepaalde waarde voor f waarden voor b en v zijn
gevonden waarvoor de vergelijking klopt, dan kunnen de waarden van b en v
ook omgewisseld worden. Als b en v niet gelijk zijn, dan levert dat dus een
tweede positie van de lens op.
d Als de lens dichter bij het lampje staat, dan valt er meer licht op de lens. Zie
figuur 7.12; 1 is groter dan 2.
Figuur 7.12
7.3
De werking van het oog
Opgave 15
Als er veel licht op valt, wordt de opening klein en als er weinig licht op valt,
wordt de opening groot.
Opgave 16
a In figuur 7.13a is de brandpuntsafstand groter (f1 is groter dan f2).
De lens is dan minder sterk.
Er is dus minder sterk geaccommodeerd.
b De beeldafstand ligt al vast. Het beeld komt op het netvlies.
De constructiestraal I (door het optisch midden van de lens) is dus alleen nodig
om de grootte van het beeld te bepalen.
c Zie de figuren 7.13a en 7.13b. AA is kleiner dan BB.
UITW ERKINGEN OPGAVEN VW O HOOFDSTUK 7
11 van 25
d Zie de figuren 7.13a en 7.13b (de overige constructiestralen II en III).
Figuur 7.13a
Figuur 7.13b
Opgave 17
a
BINAS tabel 27A
glasachtig lichaam
hoornvlies
kamervocht
ooglens
brekingsindex
1,337
1,376
1,336
1,41
sin i

 nlucht hoornvlies  1,376 
sin 60, 0

sin r
 0, 6294  r  39, 0
  sin r 
sin 60, 0
1,376

i  60, 0 
 1,376

sin r
b nho = brekingsindex van hoornvlies naar vocht in oogkamer
nlo = brekingsindex van lucht naar ooglens
nlh = brekingsindex van lucht naar hoornvlies
n
1,336
nh o  lo 
 0,971
nlh 1,376
c Zie figuur 7.14.
Bij de overgang van lucht naar hoornvlies: i = 60,0° en r = 39,0° (zie opgave
a).
Bij de overgang van hoornvlies naar vocht in oogkamer:
sin i

 nhoornvliesoogkamer  0,971
sin 39, 0

sin r
 0, 648  r  40,3
  sin r 
sin 39, 0
0,971
i  39, 0 
 0,971 

sin r
UITW ERKINGEN OPGAVEN VW O HOOFDSTUK 7
12 van 25
Figuur 7.14
d Overgang oogkamer-ooglens:
nlucht ooglens
1, 41
(noogkamer ooglens 

 1, 06  noogkamer ooglens  1)
nlucht oogkamer 1,336
 er is bij overgang van oogkamer naar ooglens breking naar de normaal toe.
Overgang ooglens-glasachtig lichaam:
nlucht glasachtig lichaam 1,337
(nooglensglasachtig lichaam 

 0,948
nlucht ooglenskamer
1, 41
 nooglensglasachtig lichaam  1)
 er is bij overgang van de ooglens naar het glasachtig lichaam breking van de
normaal af.
e Dit is onjuist. De brekingsindices zijn allemaal ongeveer gelijk. De meeste
breking vindt plaats bij de overgang van de lucht naar het hoornvlies.
Opgave 18
a Nee, je ziet alles onscherp. Onze ogen zitten namelijk zo in elkaar dat we
scherp zien als we ons in lucht bevinden. Onder water vindt er veel minder
breking plaats als het licht het hoornvlies in gaat. Dit kan in het oog niet meer
gecompenseerd worden.
b Veel zwakker. De brekingsindex van water is 1,333. Met de formule uit opgave
17 kan nu de brekingsindex van water naar hoornvlies worden bepaald. Deze is
slechts 1,032.
n
1,376
(nwater hoornvlies  lucht  hoornvlies 
 1, 032)
nlucht  water
1,333
Er vindt dus nauwelijks breking plaats.
Opgave 19
a De ooglens bij een mens is minder bol dan bij de vis. Het netvlies van de
mens is meer gekromd dan van de vis. De afstand van de lens tot het netvlies is
bij de mens groter dan bij de vis.
b De ooglens van een mens is hoofdzakelijk voor de overgang van lucht naar het
oog. De breking is dan veel sterker dan bij de overgang van water naar het oog
(zie ook vraag 18b). De ooglens van de vis moet dus sterker zijn. Voor een
redelijk goed beeld moet het netvlies aangepast worden. Door het sterker zijn
van de lens bij de vis is de afstand waarover de vis kan kijken minder groot dan
het zicht van een mens.
Opgave 20
a De beeldafstand b verandert niet. De afstand van de ooglens tot het netvlies
blijft namelijk altijd gelijk bij het oog. De voorwerpsafstand v verandert wel,
en om beide voorwerpen scherp waar te kunnen nemen moet de
UITW ERKINGEN OPGAVEN VW O HOOFDSTUK 7
13 van 25
brandpuntsafstand f ook veranderen. De ooglens wordt boller, als de
voorwerpsafstand kleiner wordt.
1
1 1 1
b
  , waarbij b constant is. is dan ook constant. De voorwerpsafstand
b
f v b
1
is eerst 10 m en daarna 2 m; v wordt dus kleiner. wordt dan juist groter.
v
1
moet dan ook groter worden, waarvoor f juist kleiner moet worden. Als de
f
brandpuntsafstand kleiner wordt, dan wordt de ooglens boller. Daarvoor moet
sterker geaccommodeerd worden.
c Bij een camera is de brandpuntsafstand juist constant. De voorwerpsafstand
verandert, en dus zal de beeldafstand ook moeten veranderen voor een scherpe
afbeelding.
d De beeldafstand wordt groter gemaakt bij een kleinere voorwerpsafstand.
1 1 1
1
is dan ook constant. De voorwerpsafstand
  , waarbij f constant is.
f v b
f
1
1
is eerst 10 m en daarna 2 m, v wordt dus kleiner. wordt dan juist groter.
v
b
moet dan kleiner worden, waarvoor b juist groter moet worden.
7.4
Nabijheidspunt en vertepunt
Opgave 21
a Het vertepunt is het punt dat het verst verwijderd is van het oog en waar je
een voorwerp nog net scherp waarneemt.
b Kijk naar een voorwerp in de verte dat je nog scherp waarneemt. Als je een bril
of contactlenzen draagt, moet je de bril afzetten of de lenzen uitdoen. Schat de
afstand tot aan dat voorwerp.
c Het nabijheidspunt is het punt waar je een voorwerp nog net scherp waarneemt
als je het voorwerp dichter naar je oog toe beweegt.
d Als je een bril of contactlenzen draagt, moet je de bril afzetten of de lenzen
uitdoen. Doe één oog dicht. Neem een pen of boek en breng dat steeds dichter
naar je oog toe. Stop als je het voorwerp onscherp waarneemt. Schat de afstand
tussen je oog en boek of pen.
Opgave 22
De voorwerpsafstand v is 30 cm, want daar bevindt de krant zich.
Het brillenglas maakt van de krant een virtueel beeld in het nabijheidspunt Noog
 afstand van Noog = b = –75 cm (b = −30 cm, negatief, want het gaat hier om
een virtueel beeld).
Invullen in de lensformule geeft: v = 30 cm en b = –75 cm.
1 1 1 1
1
5
2
3
1
   





f v b 30 75 150 150 150 50
 f  50 cm  0,50 m
1
1
S  
 2, 0 dpt
f 0,50
UITW ERKINGEN OPGAVEN VW O HOOFDSTUK 7
14 van 25
Opgave 23
a S  2,5 dpt

1

 0, 40 m  40 cm
1
1 f 
S f  
2,5
f
S
Afstand Nbril = v = 25 cm en f = 40 cm
1 1 1
  
f v b
1 1 1 1
1
   

b f v 40 25
 b  67 cm
 afstand N oog = 67 cm
b Als de persoon met een ongeaccommodeerd oog kijkt, ziet hij de voorwerpen
in het vertepunt scherp. De lichtbundel die in zijn oog valt, is dan een
evenwijdige bundel. Het vertepunt Vbril is dus het punt waarvan de divergente
lichtbundel door de lens wordt omgezet in een evenwijdige bundel. Dit is ook
te zien in figuur 7.15. Uit de eigenschappen van lenzen blijkt dat het gezochte
punt het brandpunt is. Daar moet dan nog de afstand tussen bril en oog bij
worden opgeteld. De brandpuntsafstand is 40 cm. De afstand tussen bril en oog
is 2 cm.
De totale afstand tot aan het vertepunt is dus 42 cm.
Figuur 7.15
c De oudziende kan zonder bril voorwerpen scherp waarnemen tot aan het
vertepunt Voog. Dit ligt in het oneindige. Het antwoord luidt dus ja, hij kan het
voorwerp scherp waarnemen.
d Met bril op ligt het vertepunt van de oudziende op 42 cm afstand. Voorwerpen
achter het vertepunt worden niet scherp waargenomen. Het antwoord luidt dus
nee.
e Als het oog accommodeert, kan een persoon voorwerpen scherp waarnemen
die dichterbij zijn dan het vertepunt. De oudziende kan dus voorwerpen scherp
waarnemen die dichterbij zijn dan 42 cm met geaccommodeerd oog. Het
antwoord luidt dus nee.
f De oudziende ziet met zijn bril op alleen voorwerpen scherp op een afstand
tussen 42 cm en 25 cm. Dit is op leesafstand. Voor voorwerpen op grotere
afstand dan 42 cm moet hij de bril afzetten. De bril is dus alleen bruikbaar bij
lezen.
UITW ERKINGEN OPGAVEN VW O HOOFDSTUK 7
15 van 25
7.5
Verziendheid en bijziendheid
Opgave 24
‘afwijking’ sterkte van de
ooglens
goed / te sterk / te
zwak
normaal
goed
oudziend
goed
verziend
te zwak
bijziend
te sterk
Opgave 25
accommodatie- vertepunt
vermogen
nabijheidspunt
hulplens:
positief / negatief
/ niet nodig
goed
te zwak
goed
goed
20 – 30 cm
> 30 cm
>30 cm
5 – 20 cm
niet nodig
positief
positief
negatief
oneindig
oneindig
> oneindig
< oneindig
a Hans is bijziend, want zijn lenzen zijn negatief.
1
1
1

 0, 40 m  40 cm
b SHans = –2,5 dpt; S   f Hans 
f
SHans 2,5
Zie figuur 7.16.
c Tineke is verziend, want haar lenzen zijn positief.
1
1
1

 0,50 m  50 cm
d STineke = +2,0 dpt; S   f Tineke 
f
STineke 2, 0
Zie figuur 7.16.
Figuur 7.16
Opgave 26
a Zie figuur 7.17.
Figuur 7.17
b Bij een bril is de brandpuntsafstand van de lens gelijk aan de afstand tot aan het
vertepunt. Hierbij is de afstand tussen oog en bril verwaarloosd.
f = −60 cm, negatief, want het is een bijziend persoon.
1
1
Sbril 

 1, 7 dpt
f bril 0, 60
c Zie figuur 7.18. Bij een bijziende wordt door de bril het nabijheidspunt op
grotere afstand van het oog gelegd. P is het nabijheidspunt met bril Nbril.
UITW ERKINGEN OPGAVEN VW O HOOFDSTUK 7
16 van 25
Figuur 7.18
d Nabijheidspunt met bril: v
Nabijheidspunt zonder bril: b = –20 cm
Brandpuntsafstand van de bril: f = –60 cm
Lensformule:
1 1 1
1 1 1
1
1
1
     


f v b
v f b 60 20 30
 v = 30 cm
 het nabijheidspunt met bril ligt op 30 cm afstand van het oog.
Opgave 27
a Zie figuur 7.19.
Figuur 7.19
Het vertepunt van een oog ligt altijd verder dan het nabijheidspunt. Hier is de
afstand van het vertepunt echter kleiner. Het vertepunt is dan achter het oog
terechtgekomen. Dit is het geval bij verziendheid.
b Zie figuur 7.20.
Figuur 7.20
c f = 30 cm; positief want het is een bijziend persoon.
1
1
S bril 

 3,3 dpt
f bril 0,30
d Nabijheidspunt met bril: v
Nabijheidspunt zonder bril: b = –60 cm
Brandpuntsafstand van de bril: f = 30 cm
Lensformule:
1 1 1
1 1 1 1
1
3
1
     



f v b
v f b 30 60 60 20
 v = 20 cm
 het nabijheidspunt met bril ligt op 20 cm afstand van het oog.
UITW ERKINGEN OPGAVEN VW O HOOFDSTUK 7
17 van 25
1
1
1
 f bril 

 0,50 m  50 cm
f
Sbril 2, 0
Nabijheidspunt met bril: v = 25 cm
Nabijheidspunt zonder bril: b
Brandpuntsafstand van de bril: f = 50 cm
Lensformule:
1 1 1
1 1 1 1 1
1
2
1
     




f v b
b f v 50 25 50 50
50
 b = –50 cm
 het nabijheidspunt zonder bril Noog ligt bij deze verziende op 50 cm afstand
van het oog.
Opgave 28
Sbril = +2,0 dpt; S 
Opgave 29
Sbril = –2,0 dpt; S 
1
1
1
 f bril 

 0,50 m  50 cm
f
Sbril 2, 0
Nabijheidspunt met bril: v = 25 cm
Nabijheidspunt zonder bril: b
Brandpuntsafstand van de bril: f = –50 cm
Lensformule:
1 1 1
1 1 1
1
1
1
2
3
     

 

f v b
b f v 50 25
50 50
50
50
 b    17 cm
3
 het nabijheidspunt zonder bril Noog ligt bij deze bijziende op 17 cm afstand
van het oog.
Opgave 30
a Als je zonder bril scherp kunt zien, dan kan je ooglens voldoende
accommoderen of hoeft niet te accommoderen. In dit laatste geval kijk je naar
het vertepunt. Een honderdjarige die nog voldoende kan accommoderen is
mogelijk, maar onwaarschijnlijk. Haar vertepunt ligt dus op leesafstand. De
vrouw is sterk bijziend.
b Bij bijziendheid liggen het vertepunt en nabijheidspunt te dicht bij het oog. Bij
oudziendheid komt het nabijheidspunt verder van het oog te liggen. De dochter
heeft haar vertepunt te dichtbij liggen. Ze zal dus altijd een negatieve bril nodig
hebben om in de verte te kunnen kijken. Om te kunnen lezen heeft zij eerst
geen bril nodig en later een positieve bril.
Conclusie: de vader heeft ongelijk.
Opgave 31
Om scherp in de verte te kijken, gebruikt de vrouw negatieve lenzen. Maar die
zorgen er juist voor dat het nabijheidspunt verder van het oog komen te liggen.
De oudziendheid wordt dus verslechterd door de negatieve lenzen.
Om de oudziendheid te compenseren heeft de vrouw positieve lenzen nodig.
Deze brengen niet alleen het nabijheidspunt dichterbij, maar ook het vertepunt.
Dat lag al te dichtbij, want de vrouw was bijziend. De positieve lenzen
verslechteren juist het in de verte zien.
UITW ERKINGEN OPGAVEN VW O HOOFDSTUK 7
18 van 25
7.6
Opgave 32
Gezichtshoek en loep
Een kind heeft zijn nabijheidspunt dichter bij het oog liggen. Daardoor wordt
het gat in de naald groter op zijn netvlies afgebeeld.
Opgave 33
a Ed is bijziend. Zijn nabijheidspunt zonder bril ligt dichter bij zijn oog dan
met bril.
Houdt hij het voorwerp zonder bril in zijn nabijheidspunt, dan is zijn
gezichtshoek groter en krijgt hij een groter beeld op zijn netvlies.
b Ankie kijkt naar het spiegelbeeld van haar wimpers. Om die zo duidelijk
mogelijk te zien, moet het spiegelbeeld zich in het nabijheidspunt van het oog
bevinden. Het spiegelbeeld van de wimpers bevindt zich op dezelfde afstand
van de spiegel als de afstand van de wimpers tot de spiegel. De afstand
spiegelbeeld-oog is gelijk aan de afstand van het oog tot aan het
nabijheidspunt. Ankie moet haar spiegel dus op een afstand brengen die de
helft is van de afstand van haar oog tot het nabijheidspunt.
Opgave 34
Robin houdt het voorwerp op de verkeerde afstand van de loep. Om ervoor te
zorgen dat er een evenwijdige lichtbundel uit de loep komt, moet hij het
voorwerp in het brandvlak van de loep houden. Hij kijkt dan met
ongeaccommodeerd oog.
1
1

 0,50 m;
SA 2, 0
1
1

 0,11 m
SB = 9,0 dpt  f B 
S B 9, 0
Lens A is niet als loep te gebruiken. De brandpuntsafstand is namelijk 50 cm.
De afstand tot aan het nabijheidspunt is bij de meeste mensen kleiner dan
50 cm.
De hoekvergroting wordt dan kleiner dan 1,0.
b De afstand tot aan het nabijheidspunt = Soog = 0,25 m.
De brandpuntsafstand van de loep is flens = 0,11 m.
S
0, 25
De hoekvergroting is N ang  oog 
 2,3.
f lens 0,11
c Het heeft voor Frederike geen zin om lens B als loep te gebruiken. Het
brandpunt van de lens ligt namelijk verder weg dan het nabijheidspunt.
d De brandpuntsafstand van de lens moet kleiner zijn dan de afstand tot aan haar
nabijheidspunt, dus kleiner dan 10 cm. De sterkte van de lens moet dus
minimaal zijn:
1
1
Slens 

10 dpt
f lens 0,10
Opgave 35
a SA = 2,0 dpt  f A 
Opgave 36
a Het is zinvol, omdat de medewerker dan met ongeaccommodeerd oog kijkt
en dat is minder vermoeiend.
b Teken de lichtstraal b door het knooppunt O van het oog die evenwijdig loopt
met de getekende lichtstraal a tussen de optimate en het oog. Trek die
lichtstraal door tot aan het netvlies. Zie figuur 7.21a.
UITW ERKINGEN OPGAVEN VW O HOOFDSTUK 7
19 van 25
Figuur 7.21a
Teken de randstraal c die aan het bovenste ooglid raakt evenwijdig aan de
getekende lichtstraal b. Teken deze lichtstraal c tussen de optimate en de
ooglens. Teken nu de lichtstraal d vanuit V naar waar de bovenste randstraal de
optimate raakt. Zie figuur 7.21b.
Figuur 7.21b
Teken de randstraal e die aan het onderste ooglid raakt evenwijdig met de
getekende lichtstraal c. Teken deze lichtstraal vanaf de optimate tot aan de
ooglens. Teken nu de lichtstraal f vanuit V tot waar de onderste randstraal de
optimate raakt. Zie figuur 7.21c.
Figuur 7.21c
Teken in het oog de twee randstralen g en h die vanaf de ooglens naar het
beeldpunt B gaan. Zie figuur 7.21d.
Figuur 7.21d
Arceer de bundel. Zie figuur 7.21e.
Figuur 7.21e
UITW ERKINGEN OPGAVEN VW O HOOFDSTUK 7
20 van 25
7.7
Opgave 37
Opgave 38
Enkele optische apparaten
a v  8, 0 cm  0,080 m 
1
1
1
  

 f  0, 078 m

  f 0, 080 3,5
b  3,5 m

  S  1  1  13 dpt
1 1 1
 
 
f 0, 078
f v b

b
3,5
b N 
 43, 75
v 0, 080
 het beeld is 43,75× zo groot als het voorwerp.
De hoogte van de dia = 24 mm
 de hoogte van het beeld van de dia = 24 × 43,75 = 1,1 · 103 mm = 1,1 m.
De breedte van de dia = 36 mm
 de breedte van het beeld van de dia = 36 × 43,75 = 1,6 · 103 mm = 1,6 m
 de afmetingen van het beeld zijn: 1,1 m bij 1,6 m.
c Het beeld is niet groot genoeg  je moet het beeld groter maken.
Als je het beeld groter maakt, dan wordt de beeldafstand b groter.
Als de beeldafstand b groter wordt, dan moet de voorwerpsafstand v kleiner
worden. Dit laatste volgt uit de lensformule:
1 1 1
 
f v b
 de lens verandert niet
 de brandpuntsafstand f verandert niet
1
   verandert ook niet
 f 
1 1
  = constant.
v b
1
Als de beeldafstand b groter wordt, dan wordt kleiner
b
1
 moet dan dus groter worden, dus moet de voorwerpsafstand v kleiner
v
worden
 de lens moet dichter naar de dia verplaatst worden.
De fotograaf kijkt naar het beeld op de matglazen plaat. Als het beeld daar
scherp is, moet het beeld ook scherp op de film komen. Dat betekent dat de
beeldafstand bij neergeklapte spiegel gelijk moet zijn aan de beeldafstand bij
opgeklapte spiegel.
Als de spiegel omlaag is geklapt, wordt de beeldafstand gevormd door de
afstand van lens tot spiegel plus de afstand van spiegel tot matglazen plaat. Zie
figuur 7.22a.
UITW ERKINGEN OPGAVEN VW O HOOFDSTUK 7
21 van 25
Figuur 7.22a
Als de spiegel is opgeklapt, is de beeldafstand gelijk aan de afstand van lens tot
film. Zie figuur 7.22b.
De afstand tussen lens en spiegel is in beide situaties gelijk. De afstand van
spiegel tot film moet dus gelijk zijn aan de afstand van spiegel tot matglazen
plaat.
Figuur 7.22b
Opgave 39
a v  3, 70 cm  0,0370 m   1  1  1  f  0, 03658 m
  f 0, 0370 3, 20
 
b  3, 20 m

1 1 1
  S  1  1  27,3 dpt
 
 
f v b
f 0, 0366
b
3, 20

 86, 49
v 0, 0370
 het beeld is 86,49× zo groot als het voorwerp
 het voorwerp is 86,49× zo klein als het beeld
De hoogte van het beeld = 1,80 m = 180 cm
180
 de hoogte van het display
 2, 08 cm
86, 49
De breedte van het beeld = 2,40 m = 240 cm
240
 de breedte van het display
 2, 77 cm
86, 49
 de afmetingen van het display zijn: 2,08 cm bij 2,77 cm.
c Het lcd-display in de beamer is 1024 pixels breed en 768 pixels hoog.
Op het scherm ontstaat een beeld van 1,80 m hoog en 2,40 m breed
180 cm
 0, 2344 cm
 de afstand tussen twee pixels op het scherm is:
768
240 cm
 0,2344 cm
of
1024
b N
UITW ERKINGEN OPGAVEN VW O HOOFDSTUK 7
22 van 25
De vergroting N 
afstand tussen twee punten op het netvlies
afstand tussen twee pixels op het scherm
25 106

 0, 01067
0, 2344 102
b
b 18 103
v  
 1,7 m
v
N 0,01067
Als Hanna binnen een afstand van 1,7 m van het scherm gaat zitten, kan ze de
afzonderlijke beeldpunten apart waarnemen  de minimale afstand van Hanna
tot het scherm is 1,7 m.
N
Opgave 40
a Trek de lichtstraal door het optisch midden rechtdoor tot aan de spiegel. Nu
zijn er twee mogelijkheden.
Eerste methode
Zie figuur 7.23a.
Figuur 7.23a
Teken op het spiegeloppervlak de normaal n in het punt waar de lichtstraal de
spiegel raakt.
Meet de hoek van inval (i). Teken de weerkaatste lichtstraal onder een even
grote hoek van terugkaatsing (t).
Tweede methode
Zie figuur 7.23b.
Teken het spiegelbeeld van punt B.
Om dit te doen, moet je eerst de spiegel verlengen (lijn l).
Teken vanuit B een loodlijn op de lijn l.
Het snijpunt van deze loodlijn en lijn l is punt P.
Maak de afstand BP even lang als de afstand PB (B is het beeldpunt van punt
B).
Trek de lijn BC en verleng deze lijn.
UITW ERKINGEN OPGAVEN VW O HOOFDSTUK 7
23 van 25
Figuur 7.23b
b Door het draaien van de spiegel over een hoek  wordt de hoek van inval
groter gemaakt met een waarde . De hoek van terugkaatsing wordt dan ook
groter met een waarde . De lichtstraal verdraait dus over een hoek 2.
Eerste methode
Zie figuur 7.24.
Figuur 7.24
Omdat de schaal van de tekening 1 : 15 is, is de afstand Δy in de tekening
42
 2,8 cm.
15
Het punt A wordt dus niet meer afgebeeld in punt D op het scherm, maar in het
punt C.
Teken het eindpunt C van de straal in de tekening op een hoogte van 2,8 cm.
UITW ERKINGEN OPGAVEN VW O HOOFDSTUK 7
24 van 25
Meet met je geodriehoek CSD.
CSD = 2 = 12°  de hoek waarover de spiegel is gedraaid, is 6,0°.
Tweede methode
Zie figuur 7.24.
Meet de afstand Δx op in de tekening (Δx = 12,5 cm).
Omdat de schaal van de tekening 1: 15 is, is de afstand Δx in werkelijkheid
15 × 12,5 = 187,5 cm
42
 tan  
 2  12, 6    6,3
187,5
 de hoek waarover de spiegel is gedraaid, is 6,3°.
c Het verband tussen de voorwerpsafstand v en de beeldafstand b is de
lensformule:
1 1 1
(waarbij f de brandpuntsafstand van de lens van de
 
v b f
overheadprojector is).
Zie figuur 7.24.
Doordat het beeld 42 cm hoger op het scherm terechtkomt, is de beeldafstand
groter geworden; de brandpuntsafstand is niet veranderd  de
voorwerpsafstand moet dus kleiner worden  de afstand tussen de sheet en de
lens moet kleiner worden  de kop van de overheadprojector zal omlaag
moeten.
UITW ERKINGEN OPGAVEN VW O HOOFDSTUK 7
25 van 25